
Abyssal global and deep Southern Ocean temperature trends are quantified between the 1990s and 2000s to assess the role of recent warming of these regions in global heat and sea level budgets. The authors 1) compute warming rates with uncertainties along 28 full-depth, high-quality hydrographic sections that have been occupied two or more times between 1980 and 2010; 2) divide the global ocean into 32 basins, defined by the topography and climatological ocean bottom temperatures; and then 3) estimate temperature trends in the 24 sampled basins. The three southernmost basins show a strong statistically significant abyssal warming trend, with that warming signal weakening to the north in the central Pacific, western Atlantic, and eastern Indian Oceans. Eastern Atlantic and western Indian Ocean basins show statistically insignificant abyssal cooling trends. Excepting the Arctic Ocean and Nordic seas, the rate of abyssal (below 4000 m) global ocean heat content change in the 1990s and 2000s is equivalent to a heat flux of 0.027 (±0.009) W m−2 applied over the entire surface of the earth. Deep (1000–4000 m) warming south of the Subantarctic Front of the Antarctic Circumpolar Current adds 0.068 (±0.062) W m−2. The abyssal warming produces a 0.053 (±0.017) mm yr−1 increase in global average sea level and the deep warming south of the Subantarctic Front adds another 0.093 (±0.081) mm yr−1. Thus, warming in these regions, ventilated primarily by Antarctic Bottom Water, accounts for a statistically significant fraction of the present global energy and sea level budgets.
A warming climate is unequivocal, with the global top of the atmosphere radiative imbalance currently on the order of 1 W m −2, very likely due to anthropogenic greenhouse gases (Solomon et al. 2007). Over the past few decades, roughly 80% of the energy resulting from this imbalance has gone into heating the oceans (Levitus et al. 2005), which have a large heat capacity compared with the land or the atmosphere. This warming is important in sea level rise (SLR) and other climate projections (Bindoff et al. 2007).
The earth's radiative imbalance affects SLR in two ways (e.g., Cazenave et al. 2008; Trenberth and Fasullo 2009).Much of the heat raises ocean temperature, causing thermal expansion, termed thermosteric SLR. A much smaller portion of the heat acts to melt continental ice, adding mass to the ocean. Highly accurate satellite measurements from Ocean Topography Experiment (TOPEX) / Poseidon and Jason altimetry have reported an average rate of SLR of 3.1 mm yr−1 between 1993 and 2003, with roughly half of that being due to thermal expansion and half due to mass changes, mostly from the melting of continental ice (Bindoff et al. 2007). However, there is still debate over the exact breakdown of SLR between thermostatic and mass addition components. Some recent SLR budgets using observations of upper-ocean warming and mass changes either do not close or have high uncertainty (Miller and Douglas 2004; Raper and Braithwaite 2006), especially post-2003 (Willis et al. 2008). Other SLR and global energy budgets rely on poorly constrained deep ocean heat uptake for closure (Domingues et al. 2008; Murphy et al. 2009).
Models contain a delay between greenhouse gas forcing and surface temperature increase because of the long equilibration time of the ocean (Hansen et al. 2005). Therefore, even if greenhouse gas concentrations were kept constant at current levels, ocean temperatures and sea level would continue to rise for centuries. Furthermore, model fluxes of heat from the ocean surface layers to the deep ocean differ dramatically depending on model details. This climate sensitivity affects predictions of the magnitudes and rates of future SLR and global atmospheric warming (Raper et al. 2002; Meehl et al. 2005). Indeed, uncertainty involved in deep-ocean heat uptake may be the largest cause of variation among climate projections (Boé et al. 2009), making it vital to close observed heat and SLR budgets, including the deep ocean, for the purposes of adequately constraining predictions of and preparing for future climate change.
The deep ocean is ventilated by dense water sinking at high latitudes. North Atlantic Deep Water (NADW) is a mixture of water masses formed through deep convection processes in the Nordic and Labrador Seas (LeBel et al. 2008). Antarctic Bottom Water (AABW) is formed by a complex interaction of water masses and physical processes, with varieties produced in at least three source regions: the Weddell Sea, the Ross Sea, and the Adelie Coast (Orsi et al. 1999). While pure AABW is largely confined to the Southern Ocean, here we will refer to deep and bottom waters primarily ventilated near the Antarctic as AABW for simplicity. NADW and AABW feed the deep and abyssal limbs of the global ocean meridional overturning circulation (Lumpkin and Speer 2007).
Recent studies have revealed property changes in AABW near its source regions. In the Weddell Sea, the deep water has warmed at a rate of 0.009°C yr−1 between 1990 and 1998, followed by a period of cooling (Fahrbach et al. 2004). In the Ross Sea, shelf and surface water has freshened, along with warming at middepths (190–440 m) and in the deep layer within the gyre (Jacobs et al. 2002; Ozaki et al. 2009; Jacobs and Giulivi 2010). Deep water off the Adelie Coast along 140°E has also shown cooling and freshening on isopycnals (Aoki et al. 2005; Rintoul 2007; Johnson et al. 2008a; Jacobs and Giulivi 2010).
Warming of AABW is not limited to the Southern Ocean. In the deep basins north of the Antarctic Circumpolar Current (ACC), AABW has also shown signs of warming, although at a reduced rate compared to the warming near the source regions. In the Atlantic Ocean, the abyssal water in the Scotia Sea, Argentine Basin, and Brazil Basin—all fed by AABW originating from the Weddell Sea—has warmed over the past two decades (Coles et al. 1996; Johnson and Doney 2006; Zenk and Morozov 2007; Meredith et al. 2008). In the southeastern Indian Ocean, warming has been observed in the Australian–Antarctic Basin but little change has been seen to the north (Johnson et al. 2008a). Finally, the abyssal southwest and central Pacific basins have both significantly and widely warmed over the past two decades (Fukasawa et al. 2004; Kawano et al. 2006, 2010; Johnson et al. 2007). In addition to the warming, there is some evidence of recently reduced abyssal circulation in the North Atlantic (Johnson et al. 2008b) and North Pacific (Kouketsu et al. 2009; Masuda et al. 2010).
Furthermore, the upper 1000 m of the water column throughout much of the Southern Ocean has also warmed over the last few decades, apparently at a faster rate than the upper-ocean global mean (Gille 2002, 2008; Böning et al. 2008; Sokolov and Rintoul 2009). This warming may be partly associated with a poleward migration of the ACC due to an increase in the strength and southward shift of the westerly winds that drive the ACC.
Here we make quantitative global estimates of recent (1990s to 2000s) deep and abyssal ocean warming, mostly within or originating from the Southern Ocean. We use repeat hydrographic section data to quantify temperature trends in two regions of the world's oceans: the global abyssal ocean, defined here as >4000 m in all deep basins (excluding the Arctic Ocean and Nordic seas), and the deep Southern Ocean, defined here as the region between 1000 and 4000 m south of the Subantarctic Front (SAF). AABW, as defined by a water-mass analysis (Johnson 2008), dominates much of the abyssal (Fig. 1a) global ocean and deep (Fig. 1b) Southern Ocean. The abyssal Pacific and Indian oceans are primarily composed of AABW with only a small fraction of NADW present (Fig. 1a; Johnson 2008). However, in the abyssal Atlantic, AABW dominates only in the Weddell–Enderby, Cape, Argentine, and Brazil basins, with a small fraction persisting near the bottom of the other basins, where NADW is endemic. In the deep Southern Ocean, south of the SAF, AABW also dominates (Fig. 1b; Johnson 2008). Thus, our fixed control volume (necessary for evaluating a change in heat content) contains primarily, although not solely, AABW, and it allows for an estimate of warming due to changes in waters mostly of southern origin.
Fig. 1. (a) Tracklines of the 28 repeated sections studied (black lines) with WOCE designators noted adjacent. Basin boundaries are outlined (gray lines) over the depth-averaged fraction of AABW below 4000 m (color bar) after Johnson (2008). The Subantarctic Front (SAF; Orsi et al. 1995) position (magenta line) and the 4000-m isobath (thin black lines) are also shown. (b) As in (a) but a polar projection with tracklines of the nine repeated sections that extend south of the SAF plotted over the depth-averaged fraction of AABW from 1000 to 4000 m with the 1000-m isobath and without basin boundaries.
We describe the repeat hydrographic data and screening methodologies used in section 2. In section 3, we describe regional rates of temperature change and estimate their uncertainties from these data. In section 4, we use these rates to calculate the contributions of warming primarily of southern origin to heat and SLR budgets in two ways: first, we calculate local abyssal contributions for individual ocean basins and the deep Southern Ocean (section 4a); and second, we combine abyssal contributions from all 32 basins (assuming unsampled basins do not change) and the deep Southern Ocean for a global assessment (section 4b).We explore the effects of variations in our 4000-m boundary between global abyssal and deep Southern Ocean volumes near the end of section 4. We conclude with a discussion of the results in section 5.
High-quality temperature observations of the global deep ocean originate mostly from ship-based conductivity- temperature-depth (CTD) instruments. The international World Ocean Circulation Experiment (WOCE) Hydrographic Programme accomplished a full-depth high-resolution, high-accuracy, hydrographic survey of the global ocean in the 1990s, with coast-to-coast zonal and meridional sections crossing all major ocean basins. A key subset of these sections is being reoccupied in support of the Climate Variability and Predictibility (CLIVAR) and Carbon Cycle Science Programs, now coordinated by the international Global Ocean Ship-based Hydrographic Investigations Program (GO-SHIP). All occupations of the repeat sections that had publicly available CTD data posted online (at http://cchdo.ucsd. edu) as of July 2010 are considered here. Thus, the dataset used for this study is an aggregate of 28 full-depth, high-quality hydrographic sections that have been occupied two or more times between 1981 and 2010 (Figs. 1, 2). Throughout this study sections are referred to by their WOCE identification.
The first occupation of most sections was in the 1990s during WOCE with subsequent occupations, mostly during the 2000s, in support of the CLIVAR and Carbon Cycle Science Programs (Fig. 2). The nine sections with occupations prior to 1990 were sampled during the ramp-up to WOCE with the earliest occupation considered here being the 1981 occupation of A05. The most recent occupation included in this study is also of A05, completed in February 2010. Sections have a minimum of one occupation during WOCE followed by a second occupation 6–12 years later, with the exceptions of A01, A02, P03, and A13.5 (Fig. 2). Both A01 and A02 have multiple occupations available, but only in the 1990s. P03 and A13.5 were occupied in the 1980s and 2000s but have no occupations in the 1990s. The shortest time interval between the first and last occupation of a section is 3 years, for A02, from 1994 to 1997; the longest interval is 29 years, for A05, from 1981 to 2010. The mean and median time differences between first and last occupations for repeat sections are 12.9 and 11.9 yr, respectively.
Fig. 2. Occupation dates for each of the 28 repeated sections analyzed here listed by their WOCE designators (see Fig. 1 for locations). Lines extend over the entire period over which data were collected for a given occupation of a section. Longer lines indicate where multiple legs of sections taken over the course of up to a year or more are joined.
Data collected along each section are highly accurate and well sampled in the vertical and horizontal. Vertical profiles of temperature, conductivity, and pressure were collected at each station from the surface to a depth of 10–20 m from the bottom using a CTD. Horizontal station spacing was nominally 55 km, often less over rapidly changing bathymetry. Salinity was calculated from CTD conductivity, temperature, and pressure data and calibrated to bottle samples standardized with International Association for the Physical Sciences of the Oceans (IAPSO) standard seawater using the 1978 practical salinity scale (PSS-78). All temperature analysis here uses the 1968 international practical temperature scale (IPTS-68), applicable to the 1980 equation of state (EOS-80). WOCE (and GO-SHIP) CTD accuracy standards are 0.002 PSS-78 for salinity, 0.002°C for temperature, and 3 dbar for pressure (Joyce 1991). Some GO-SHIP cruises may achieve 0.001°C temperature accuracy.
We screen data prior to analysis based on two criteria: first, only data with good quality flags are used, and, second, each section is visually inspected to determine if the trackline of any given occupation was close enough to those of other occupations for comparison. Here trackline refers to the zonal or meridional line along which the sampling stations fell (as opposed to the locations of the stations themselves), typically following a nominal latitude or longitude (Fig. 1). Tracklines of reoccupations of most sections used here lie within 10 km of the original, with four exceptions: First, at the west end of A05 between 69° and 76°W the 1998, 2004, and 2010 occupations lie ∼220 km to the north of the 1981 and 1992 occupations. Second, the tracklines of the 1993 and 2003 occupations of A16 diverge by up to 88 km between 2° and 12°N. Third, south of 20°S along P16 the tracklines are consistently ∼40 km apart. Finally, between 85° and 91°W along I05 the trackline of the 1995 occupation reaches distances as much as 55 km from the tracklines of the 2002 and 2009 occupations. These variations are deemed useable because they occur in areas of small deep horizontal density gradients. However, in other areas where tracklines diverge by less than 200 km the data are not used here because the divergences occur in regions of large deep horizontal density gradients, such as the Southern Ocean. In addition, any data from tracklines falling on opposite sides of deep ridges are not used in this study.
The sections analyzed here were not necessarily occupied in a single leg by one ship (Fig. 2). Many of them were broken into multiple segments that sometimes span more than a single calendar year. These segments are aggregated into a single section for this analysis. Sections with more than one occupation in a single calendar year are treated as if all stations measured in that year were from one occupation. This aggregation applies to 14 sections: the 1990, 1991, 1992, 1994, 1995, 1996, and 1997 occupations of A01; the 1988/89 occupation of A16; the 1994/95 and 2007 occupations of I08/I09; the 1995 occupation of I09S; the 1999 and 2007 occupations of P01; the 1993/94 occupation of P02; the 2005/06 occupation of P03; the 1992 and 2003 occupations of P06; the 1992/93 and 2007 occupations of P14; the 1992 and 2005 occupations of P16; the 1991–93 occupation of P17; the 1994 and 2008 occupations of P18; the 1994 and 2009 occupations of P21; and the 1995 occupation of SR03.
We interpolate data for each occupation of the 28 studied sections onto closely spaced vertical and horizontal grids along their tracklines for analysis. First, potential temperature (θ) is derived from the 2-dbar CTD data at each station. The station θ profiles are then low passed vertically with a 40-dbar half-width Hanning filter and interpolated onto a 20-dbar vertical grid. At each pressure, the data are then interpolated onto an evenly spaced standard 2′ longitudinal or latitudinal grid along the section trackline using a space-preserving piecewise cubic Hermite interpolant. The horizontal grid chosen matches a 2′ bathymetric dataset derived from merging satellite altimetry data and bathymetric soundings (Smith and Sandwell 1997). The bathymetric dataset and the measured CTD maximum pressures for each station are used to mask interpolated data located below the sea floor. In addition, interpolated data are discarded between any gaps in station spacing exceeding 2° of latitude or longitude along a trackline.
We calculate a rate of change in θ with time (dθ/dt) at every vertical and horizontal grid point along each trackline using data from all occupations of that section where the time between the first and last occupation exceeds 2.5 yr. In places with only two occupations, dθ/dt is calculated by dividing the θ change between occupations by the time between occupations. For sections with more than two occupations, at each grid point a line is fit to θ data versus time using least squares, allowing estimates of both dθ/dt and its uncertainty from the slope of the line and its error (Fig. 3). Here we assume that errors owing to spatial and temporal variability discussed immediately below dominate and ignore slope uncertainties and the comparatively small instrumental errors of 0.001°–0.002°C. We construct pressure–latitude or pressure–longitude sections of dθ/dt estimates for each repeat section (e.g., Fig. 4). Generally, sections with three or more occupations evince amonotonic temperature trend with time on basin scales. For instance, the warming rates in the southwest Pacific basin among the three distinct pairs formed by the three occupations of P06 (a trans-Pacific section along 32°S, Fig. 1) are grossly similar (Fig. 5). While there is variability among the three rate estimates at any given depth and the estimate over the longest time interval is smoothest in the vertical, using any two of the three occupations would result in a similar depth-averaged rate of abyssal warming.
Fig. 3. Local dθ/dt estimate for a location with more than two section occupations. Potential temperature data (asterisks) from three occupations along P18 (see Fig. 4, green asterisk, for location) at 56°S and 4000 dbar plotted vs time are used to fit a line by least squares (solid line), producing an error estimate here shown at 95% confidence limits (dotted line). The slope of the line is dθ/dt.
Fig. 4. Time rate of change of potential temperature dθ/dt (color bar), along the trackline of P18 (see Fig. 1 for location). Areas of warming are shaded in red, and regions of cooling are shaded in blue with intensity scaled by the magnitude of the change. Mean θ values over all occupations are contoured (black lines). This trackline is grouped into four basins for analysis (boundaries shown by vertical black lines), and the area south of the SAF (vertical dotted–dashed line) is also analyzed separately. The basins from south to north are the Amundsen–Bellingshausen Basin, Chile Basin, Peru Basin, and central Pacific Basin. Green asterisk denotes location of data used in Fig. 3.
Fig. 5. Mean time rate of change in potential temperature dθ/dt at each pressure along the portion of P06 crossing the southwest Pacific basin (Fig. 1) calculated using every combination of pairs of the three occupations of P06 (see legend).
The dθ/dt contours along section tracklines reveal vertically banded structures extending throughout the water column (Fig. 4). These vertical structures are most likely due to mesoscale ocean eddies, internal waves, and tides that cause vertical displacements of isopycnals. To evaluate the statistical significance of large-scale dθ/dt patterns observed in the face of such variations, a robust estimate of a characteristic horizontal decorrelation length scale is required to calculate the effective degrees of freedom (DOF). To evaluate the length scale of these features, at every pressure level along each trackline, we remove unsampled (masked) grid points, and then find the maximum of the integral of the spatially lagged autocovariance of the spatially detrended warming rate, following Johnson et al. 2008a. Twice this integral gives an estimate of the horizontal decorrelation length scale.
The horizontal decorrelation length scale varies among sections, with values ranging from 25 to 400 km, but generally clustering near 160 km (Fig. 6). The decorrelation length scales estimated from each section are relatively constant vertically from about 500 to 5000 dbar because energetic vertical features in dθ/dt tend to be coherent throughout the water column. Deeper than 5000 dbar the length scale gradually tends toward zero with depth, as the sampled region gets smaller and smaller, and there are more breaks in the sections owing to intervening topography. Shallower than 500 dbar, the length scales sometimes get longer, perhaps owing to large-scale wind-driven shifts in gyre positions or aliasing of the seasonal cycle. At each pressure surface, using repeat sections with lengths greater than 2000 km, we calculate the median of the horizontal decorrelation length scale (Fig. 6). There are 25 sections longer than 2000 km at the surface, but this number decreases with depth to only 11 sections by 5000 dbar. Between 500 and 5000 dbar, the median is fairly constant around 163 km. The vertical mean and median of the median between 500 and 5000 dbar are both 163 km. This value is used throughout this study as our best estimate of the horizontal length scale for all sections at all pressures. We chose the 2000-km section-length criterion based on an examination of decorrelation-length scale estimates versus section length (not shown). For sections longer than 2000 km the decorrelation-length scale estimates asymptotically approach a common value. The criterion chosen ensures the sections used for the decorrelation-length scale estimate sample this length scale roughly a dozen times or more.
Fig. 6. Horizontal decorrelation length scales (km) of dθ/dt for each of the 28 repeat sections (gray lines) calculated at each pressure. The median (thick black line) and quartiles (thin black lines) are calculated from all sections with horizontal lengths greater than 2000 km at a given pressure. The pressure-averaged mean and median of the median length scale from 500 to 5000 dbar is 163 km.
For this analysis we divide the ocean into 32 deep basins (Fig. 1) based on bottom topography (Smith and Sandwell 1997) and climatological ocean bottom temperature (Gouretski and Koltermann 2004). The boundaries for the basins follow the major ocean ridges, most of which are shallower than 3000 m. Most of the 32 deep basins were crossed by at least one section, with the exception of the Arabian Sea and Somali Basin in the northwest Indian Ocean (Fig. 1). A few marginal seas (the Sea of Okhotsk, Sea of Japan, Philippine Sea, Guatemala Basin, Panama Basin, and Gulf of Mexico) are also unsampled, but these are all mostly shallower than 4000 dbar, and thus have a minor impact on our study. The Arctic Ocean and Nordic seas, which contain little or no AABW, were not sampled by the available repeat sections analyzed here, and thus are not included in this study.
We estimate a mean warming rate and its associated uncertainty at each pressure horizon for each of the 24 deep basins sampled (e.g., Fig. 7). For these estimates, we divide the sections at the basin boundaries and calculate the mean and standard deviations of the warming rates on isobars within each basin. If a basin only has one section crossing it, the means and standard deviations for the single section within the basin as a function of pressure are assumed to be representative of the whole basin. If a basin is crossed by more than one section, the length-weighted means and standard deviations are calculated using data fromportions of all sections crossing that basin at each pressure level. For example, the mean du/dt for the Amundsen–Bellingshausen Basin of the southeast Pacific (Fig. 7) estimates warming of about 0.002°C yr−1, statistically different from zero at 97.5% confidence below about 3500 m. This result might be anticipated from examination of the warming rate along the P18 section (Fig. 4), which is the major contributor to this estimate, augmented only by a small portion of the southern end of P16 that also enters the basin (Fig. 1). We discuss the assumption that the length-weighted temperature trend statistics for the repeat hydrographic section tracklines crossing each basin are representative of the entire basin further in section 5.
Fig. 7. Mean (thick black line) and 95% confidence limits (thin black lines) of dθ/dt for the Amundsen–Bellingshausen Basin calculated as described in the text, a length-weighted combination of the portions of repeated sections that cross the basin (in this instance P18 and P16, see Fig. 1 for locations).
At each pressure level we compute the DOF for each section crossing the basin by dividing the horizontal length of the section at that pressure by the single horizontal decorrelation length scale of 163 km. In areas where topography isolates the sampled regions such that one region is continuously sampled in the horizontal over a distance less than the decorrelation length scale, and that region is separated from adjacent sampled regions by distances more than the decorrelation length scale, the data from the region in question are assumed to be statistically independent and to contribute one DOF to the estimate. The DOF at each pressure within each basin is the sum of the DOF for all sections that cross that basin. The standard deviation is converted to a standard error by dividing by the square root of the DOF, and the two-sided 95% confidence interval is estimated assuming a Student's t distribution.
In each basin where measurements do not extend to the deepest portions of that basin, the deepest estimate of dθ/dt is applied to the deep unsampled portions of that basin. Prior to this operation, each basin is visually inspected to make sure that the deepest estimate is well below the sill depth of that basin and that the volume of water below the deepest estimate is small compared to the volume of the basin.4000 m. If these conditions are not met, the extension is not applied.
In addition to these basin-based warming estimates using physical topographical boundaries, we make one other estimate of du/dt for the entire Southern Ocean. We use an estimate of the location of the SAF (Orsi et al. 1995), which demarks the northern edge of the ACC, as the northern boundary for the region. Even though it is not a physical boundary, the SAF acts as a dynamical boundary separating water masses. While the SAF moves in time and has trended south slightly over recent decades (Gille 2008; Sokolov and Rintoul 2009), a time-invariant control volume is required for heat and sea level budgets, so motions of the SAF are not considered in this analysis. South of the SAF, isotherms rise steeply, indicating that the cold dense water of Antarctic origins found only in very deep regions to the north of the SAF extends to shallower ranges of the water column to the south of the SAF (Figs. 1b and 4). The eight meridional and one zonal section that sample regions south of the SAF (Fig. 1b) are grouped together to estimate the warming rate along pressure horizons in the Southern Ocean. The meridional sections are reasonably evenly spaced around the globe and give good coverage of the south Indian and South Atlantic oceans. However, there is only one section in the South Pacific Ocean (P18, located on the eastern side, see Fig. 1) that approaches even the base of the Antarctic continental rise, so this region is underrepresented in the final estimates of Southern Ocean changes.
The warming rate of the entire Southern Ocean south of the SAF is estimated at each pressure. Using the same method described above for basins with multiple crossings, the nine sections with data south of the SAF (Fig. 1b) are used to find the length-weighted means and 95% confidence intervals of the warming rate in the Southern Ocean. As mentioned above, owing to the spatial distribution of available data, these values are somewhat biased toward θ changes in the south Indian and South Atlantic oceans over the South Pacific Ocean and thus might be more representative of property changes originating from Weddell Sea or Adelie Land Bottom Water rather than those originating from Ross Sea Bottom Water. In addition, since not all the tracklines extend to the Antarctic continental rise (Fig. 1b), the northern portions of the Southern Ocean may also be overrepresented in the warming rates for the Southern Ocean presented here.
We focus here on the effects of 1990s to 2000s warming of abyssal waters globally and deep waters in the Southern Ocean on heat gain and SLR. First, given the observed dθ/dt within a given depth range in each basin, we estimate the local heat flux required across the top of that depth range in each basin to account for that change and the local SLR implied by that change in each basin (section 4a). Second, we make a global estimate of the heat flux required to account for the sum of changes in individual basins and given depth ranges expressed as if the heating were distributed evenly over the entire surface of the earth (a climate literature convention) and, similarly, a global estimate of SLR expressed as a uniform change in height of the entire ocean surface (section 4b).
In many of the basins north of the SAF, warming trends on pressure levels become significantly different from zero at 97.5% confidence below around 4000 m, making this depth a natural division for this study. In many of the repeat sections within the Southern Ocean consistently strong warming extends higher in the water column south of the SAF. Hence, we also analyze contributions to SLR and heat gain from warming found from 1000 to 4000 m south of the SAF. We sum the changes found in these two regions (1000–4000 m south of the SAF and below 4000 m everywhere but the Arctic Ocean and Nordic seas). Both of these regions are primarily ventilated by AABW (Fig. 1; Johnson 2008), so our estimates may be loosely thought of as quantifying the effects of changes in AABW on local and global heat and sea level budgets, although other Southern Ocean changes likely also play a role, as discussed in section 5.
To calculate the local contribution of warming in each basin below 4000 m to the heat budget, dθ/dt estimates are converted to a heat flux ( Qi ) through the 4000-m isobath of each basin using
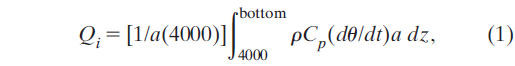
where a is the surface area of each depth, z, calculated using a satellite bathymetric dataset (Smith and Sandwell 1997). Prior to this integration, the dθ/dt profiles are interpolated from a pressure grid onto an evenly spaced 20-m depth grid for each basin. Profiles of density ρ and heat capacity Cp are estimated from climatological data (Gouretski and Koltermann 2004) for each basin using the mean temperature and salinity at each depth within that basin. The integral in (1) gives the total heating rate below 4000 m in each basin. Dividing by the surface area of the basin in question at 4000 m, a(4000), converts the total heating rate into a flux required through the 4000-m level in that basin to account for the observed warming beneath that level in that basin (Fig. 8a).
Fig. 8. (a) Mean local heat fluxes through 4000 m implied by abyssal warming below 4000 m from the 1990s to the 2000s within each of the 24 sampled basins (black numbers and color bar) with 95% confidence intervals. The local contribution to the heat flux through 1000 m south of the SAF (magenta line) implied by deep Southern Ocean warming from 1000 to 4000 m is also given (magenta number) with its 95% confidence interval. (b) Similarly, basin means of sea level rise from the 1990s to the 2000s due to abyssal thermal expansion below 4000 m and deep thermal expansion in the Southern Ocean from 1000 to 4000 m south of the SAF. Basin boundaries (thick gray lines) and 4000-m isobath (thin black lines) are also shown.
We find the 95% confidence interval associated with the Q for each basin using the volume-weighted variance of Q and volume-weighted DOF for that basin. The variance (standard deviation squared) of dθ/dt at each pressure in each basin is converted to a heating rate variance by multiplying by the square of ρCp. Then, the volume-weighted means for the variance and DOF below 4000 m are found using the a at each depth for a weight in the vertical integration. The standard deviation is then found by taking the square root of the variance and again the 95% confidence interval estimated assuming a Student's t distribution (Fig. 8a).
Similarly, we calculate the local SLR due to thermal expansion of each basin below 4000 m Fi using
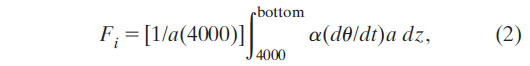
where α is the thermal expansion coefficient. The associated 95% confidence intervals for each Fi are estimated following a method analogous to that described above for the local heat budget estimates (Fig. 8b).
The geographical distributions of local basin-mean warming and cooling below 4000 m from the 1990s to the 2000s (Fig. 8a) and closely associated SLR changes (Fig. 8b) reveal a clear global pattern. Of the 24 basins with data below 4000 m, 17 warmed (nine significantly different from zero at 97.5% confidence) and 7 cooled (one significantly different from zero at 97.5% confidence).
In general, a clear pattern in the magnitude of abyssal heating is seen: smaller values farther to the north and larger values to the south (Fig. 8). The three southernmost basins—the Weddell–Enderby, the Australian–Antarctic, and the Amundsen–Bellingshausen—show strong local warming below 4000 dbar of 0.33 (±0.28), 0.25 (±0.14), and 0.15 (±0.11) W m−2, respectively, all significantly different from zero at 97.5% confidence. We can trace the propagation of AABW from these southernmost basins northward and, with it, a waning warming (or cooling) signal. In each of the three oceans, AABW flows generally north from basin to basin, subject to bathymetric constraints. However, the Atlantic, Indian, and Pacific oceans each present a slightly different pattern that should be viewed with the AABW flow in mind, as discussed below.
In the Atlantic Ocean, the warming pattern follows the flow of AABW out of the Southern Ocean. AABW leaves the Weddell Sea across the South Scotia Ridge and through the Sandwich Trench, traveling toward the western North Atlantic through the Argentine and Brazil basins in the western South Atlantic (Coles et al. 1996; Orsi et al. 1999; Jullion et al. 2010). The Argentine and Brazil basins, containing mostly AABW in the abyss (Fig. 1a; Johnson 2008), show warming, with that of the latter being statistically significant. The abyssal western North Atlantic, which contains little AABW influence, shows only a small amount of warming, not significantly different from zero (Fig. 8). At the equator, deep and bottom waters cross into the Angola Basin and travel north and south, filling the basins east of the Mid-Atlantic Ridge through deep passages (Warren and Speer 1991). These eastern Atlantic basins all show abyssal cooling with the northernmost basin being the only one showing statistically significant cooling in this study. However, the dominant abyssal influence in these eastern basins is NADW, not AABW (Fig. 1; Johnson 2008). On the other hand, the strong and statistically significant recent warming in the deep Caribbean Sea, filled with NADW that spills over a relatively shallow ∼1800-m sill, is part of a trend starting a few decades prior to the 1990s (Johnson and Purkey 2009).
In the Indian Ocean both warming and cooling basins are found (Fig. 8). Basins to the west of the Ninetyeast Ridge mostly show deep cooling, although none of these basins exhibits cooling significantly different from zero at 97.5% confidence, while the two basins to the east of the ridge show statistically significant warming. Two of the basins west of the Ninetyeast Ridge, the Somali Basin and Arabian Sea, are not sampled. Since the deepest sills of these basins connect them to adjacent basins exhibiting cooling, one could speculate that these unsampled basins might have shown cooling had they been sampled repeatedly, although the adjacent cooling is not statistically different from zero at 97.5% confidence. As in the Atlantic, the magnitude of the warming (or cooling) in the Indian Ocean basins decreases with distance from the Southern Ocean. The warming Agulhas–Mozambique Basin, located directly south of Africa between the cooling Cape Basin in the southeast Atlantic Ocean and the cooling Crozet and Madagascar Basins in the southwest Indian Ocean, stands out as an anomaly to this pattern. Data from two tracklines crossing the dynamic Agulhas–Mozambique Basin were used in this calculation (Fig. 1a): I05 shows uniform cooling across the northeast region of the basin, but I06 alternates between warming and cooling while crossing the fronts of the ACC. Hence, these data estimate overall warming in the basin, but with a large uncertainty.
In contrast to the Atlantic and Indian oceans, the Pacific Ocean (Fig. 8) exhibits deep warming that is significantly different from zero at 97.5% confidence in its large central basins with more uncertain warming in most of its small peripheral basins. One of the peripheral basins shows very slight (0.01 W m−2) but statistically insignificant cooling. Similar to the other two oceans, the magnitude of the warming in the Pacific basins decreases northward from the Southern Ocean.
To complement the local estimates of warming and SLR below 4000 m, Q and F are calculated for the region between 1000 and 4000 min the Southern Ocean south of the SAF, where AABW influence is also strong (Fig. 1b; Johnson 2008). Equations (1) and (2) are applied following the same procedure as described above but using the area and dθ/dt from the Southern Ocean. The heating between 1000 and 4000 m in the region contributes an additional 0.91 (±0.82)W m−2 and 0.87 (±0.76) mm yr−1 to the local heat flux and SLR, respectively. Adding these local changes to the heat flux and SLR below 4000 m in the Southern Ocean yields local heat gains equivalent to a local heat flux on the order of 1 W m−2 and SLR on the order of 1 mm yr−1.
The observed local heat flux and SLR are combined in rough estimates of the recent abyssal and deep Southern Ocean warming's contributions to global heat and SLR budgets. The total heat flux and error at each depth can be calculated by summing the results fromall basins using
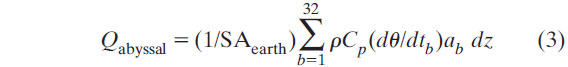
and the 95% confidence interval on that sum estimated using
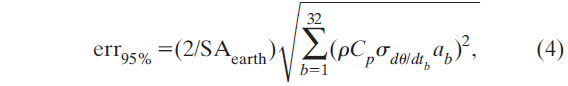
where SAearth is the total surface area of the earth and the subscript b denotes each basin (Fig. 9a). The global heat flux is expressed in terms of an application to the total surface of the earth, as is customary for global energy budget studies, rather than the surface area of the ocean.
Fig. 9. Profiles of heat gain per meter (thick lines) with 95% confidence intervals (thin lines) estimated as described in (3) for the (a) global ocean and (b) Southern Ocean south of the SAF. Area-weighted mean profiles of dθ/dt for (c) the global ocean and (d) the Southern Ocean south of the SAF.
The factor of 2 in (4) yields a conservative estimate for the 95% confidence limits from a Student's t distribution. The DOF of the 24 sampled basins ranges from 4 to 283 with a mean and median of 37 and 23, respectively. The estimate in each basin is independent, making the DOF easily greater than 60, thus this factor could arguably be slightly less than 2. The eight basins that were not sampled are assumed to have a zero warming rate.
The contribution of the Southern Ocean Q (Fig. 9b) to the global heat budget can be derived by dividing by SAearth instead of the basin surface area in (1). Again, we express this contribution as a uniform heat flux applied to the entire surface area of the earth. Comparing the global heat flux (Fig. 9a) to the heat flux south of the SAF (Fig. 9b) further emphasizes the result (Fig. 8) that the abyssal temperature changes contribute a statistically significant fraction of the observed global change in addition to the deep Southern Ocean warming. Above 4000 m almost all of the deep warming can be accounted for by warming in the Southern Ocean, again supporting the choice made here of focusing on global abyssal changes below 4000 m and Southern Ocean deep changes from 1000 to 4000 m.
Area-weighted mean dθ/dt profiles for the global and Southern oceans (Figs. 9c,d) emphasize that the deep warming rate in the Southern Ocean is much larger than that in the global ocean. Also, warming temperature trends remain strong to the bottom; contributions of abyssal warming to the heat budget decrease with increasing depth primarily because the area of the ocean decreases with increasing depth.
We make an estimate of the total heat gain from recent deep Southern Ocean and global abyssal warming by adding the integral of Qabyssal below 4000 m to the integral of QSouthernOcean from 1000 to 4000 m (Table 1). The 95% confidence interval for Qabyssal is calculated as the square root of the sum of the basin standard errors squared times 2, again using this factor because the DOF exceed 60. The warming below 4000 m is found to contribute 0.027 (±0.009) W m−2. The Southern Ocean between 1000 and 4000 m contributes an additional 0.068 (±0.062) W m−2, for a total of 0.095 (±0.062) W m−2 to the global heat budget (Table 1). Following the same procedure, the contribution of these warmings to SLR due to thermal expansion can be estimated using α instead of ρCp and the surface area of the ocean instead of the surface area of the earth. A global contribution of 0.145 (±0.083) mm yr−1 of SLR can be linked to this thermal expansion (Table 1).
The above calculations assume that the unsampled basins give zero contribution to the heat budget. We investigate the effects of two alternative scenarios on the estimates. For the first scenario, we assume that the unsampled basins have a dθ/dt profile equal to the mean dθ/dt profile of all the sampled basins. This scenario increases our global abyssal estimate by 0.0006 W m−2. For the second scenario, we assume that the unsampled basins have a dθ/dt profile identical to that of the adjacent basin with the deepest connecting sill upstream in terms of abyssal flow, where the abyssal water supplying the basin in question likely originated. The two unsampled deep basins in the Indian Ocean—the Somali Basin and Arabian Sea—are assumed to be connected to the Madagascar Basin and mid-Indian Basin, respectively. In addition, dθ/dt of the central Pacific basin is used for the Sea of Okhotsk, Sea of Japan, and the Coral Sea, and dθ/dt of the Peru Basin is used for the Guatemala and Panama Basins. However, as mentioned earlier, all of these basins are either completely or mostly shallower than 4000 m; therefore, they have little impact on the estimates given here. The scenario decreases the global mean estimate of deep Southern Ocean and global abyssal heat gain by 0.0009 W m−2. Thus, for either of these methods of accounting for the unsampled basins, the global values remain identical at the quoted precision (Table 1).
In addition to using 4000 m as the shallower limit for the global abyssal estimate and the deeper limit for the deep Southern Ocean estimate of warming, we also present global heat flux and SLR estimates using 3000 and 2000 m for that dividing depth (Table 1). We believe that 4000 m is the more appropriate choice for quantifying primarily the effects of AABW warming. However, since the deepest known studies of ocean heat uptake of which we are aware extend only to 3000 m (Levitus et al. 2005) and the Argo array allows estimates to 2000 m since about 2003 (e.g., von Schuckmann et al. 2009), we calculate the global flux and SLR below 3000 and 2000 m for comparison with these works. The 2000-m numbers should be used with caution. Above 3000 m, changes along a given section may be influenced by changes in the wind-driven circulation (e.g., Roemmich et al. 2007), requiring better temporal and spatial sampling than available from repeat hydrography to quantify properly. Thus, we may be underestimating uncertainties above 3000 m since we may be aliasing wind-driven processes that are not captured by the spatially sparse and decadal sampling scheme.
When 3000 m is used instead of 4000 m, the same local basin patterns emerge (not shown). The only basin where the mean changes sign is the South Fiji Basin,which trends from warming at 0.00 W m−2 to cooling at 0.02 W m−2. The error-to-signal ratio for local heating rates below 3000 m increases substantially in many of the basins compared with that below 4000 m, with none of the basins' cooling being statistically significant. Using a 2000-m interface depth gives an even higher abyssal heat flux (not shown), also with an even higher error-to-signal ratio.
Again, following (3) and (4), the recent decadal global heat gain in the deep ocean can be estimated by adding Qabyssal below 3000 (or 2000) m to the QSouthernOcean between 1000 and 3000 (or 2000) m (Table 1). As expected, using this 3000-m interface the global contribution below 3000 m increases compared to that below 4000 m. The Southern Ocean contribution, between 1000 and 3000 m is less than between 1000 and 4000 m. The sum, however, is roughly the same. Similarly, using the 2000-m interface depth raises the global contribution but lowers the Southern Ocean contribution with the sum remaining roughly the same. Again, these similarities exist because most of the observed warming between 2000 and 4000 m is located in the Southern Ocean (Fig. 9), and therefore choosing 4000, 3000, or 2000 m does not change the heat gained by the ocean below that interface north of the SAF. However, the partition of error associated with the estimates shifts as the interface depth is changed. The abyssal contribution has a signal 3.2 times its 95% confidence with the 4000-m interface, but only 1.7 (1.1) times its confidence using 3000 (2000) m because the bottom-intensified abyssal warming signal is most robust near the bottom.
We make three large assumptions in constructing the abyssal basin estimates of heat gain and SLR below 4000 m and the deep Southern Ocean estimates of these quantities from 1000 to 4000 m. First, we assume that dθ/dt within a given basin or the Southern Ocean is relatively consistent over the pressure intervals considered. This assumption is often supported by examination of pressure–latitude/longitude sections of dθ/dt estimates, wherein dθ/dt is often roughly vertically uniform on deep pressure horizons, and more so below the sill depth of a basin. For example, P18 crosses four basins: the Amundsen–Bellingshausen, Chile, Peru, and central Pacific (Fig. 4). The Chile and Peru Basins both show uniform (but small) warming below 3000 m and exhibit little variability, while the Amundsen–Bellingshausen Basin shows stronger warming but also higher variability. Second, we assume that the tracklines used to estimate warming rates in each basin or region are representative samples of that basin. The validity of this assumption is dependent on the spatial coverage of the tracklines. In the basins that have multiple meridional and zonal crossings, this assumption seems valid. However, in a few of the basins, such as in the Philippine Sea and the Amundsen–Bellingshausen Basin, repeat sections cross only a small portion of the basin. In these cases, the changes seen in the single region are applied to the whole basin (Fig. 1). Generally, the error analysis ensures that the uncertainties for these basins, with their limited DOF, are appropriately large. The third assumption is that the time scale of the dθ/dt changes observed is longer than the intervals between occupations. This assumption generally seems valid because different sections taken over different time intervals in the same basin yield similar estimates of dθ/dt (e.g., Fig. 5) and a consistent large-scale geographical pattern emerges from the analysis (Fig. 8).
While we focus on deep warming of Antarctic origin here, the temperature and salinity of NADW also varies significantly on interdecadal time scales (Yashayaev and Clarke 2008), with implications for long-term warming (Levitus et al. 2005). Our study includes some of this recent variability, especially in the abyssal North Atlantic. However, the deep Nordic seas have also warmed at a rate around 0.01°C yr−1 during the 1990s (Osterhus and Gammelsrod 1999; Karstensen et al. 2005). The local heat flux that would be needed to account for the warming in theGreenland Sea below 1500 m since 1989 is on the order of 50 W m−2 (Karstensen et al. 2005), with a similar value for the warming in the deep Norwegian Sea starting in 1980 (Osterhus and Gammelsrod 1999). These marginal seas are neither ventilated by AABW nor sampled by repeat hydrographic data available at the CLIVAR and Carbon Hydrographic Data Office (CCHDO), so are excluded from our study. However, if the Arctic Ocean and Nordic seas had been included, the global heat flux estimates for below 2000, 3000, and 4000 m presented here could have increased.
The heating reported here is a statistically significant fraction of previously reported upper-ocean heat uptake. The upper 3000 m of the global ocean has been estimated to warm at a rate equivalent to a heat flux of 0.20 W m−2 applied over the entire surface of the earth between 1955 and 1998 with most of that warming contained in the upper 700 m of the water column (Levitus et al. 2005). From 1993 to 2008 the warming of the upper 700 m of the global ocean has been reported as equivalent to a heat flux of 0.64 (±0.11) W m−2 applied over the earth's surface area (Lyman et al. 2010). Here, we showed the heat uptake by AABW contributes about another 0.10 W m−2 to the global heat budget. Thus, including the global abyssal ocean and deep Southern Ocean in the global heat budget could increase the estimated ocean heat uptake over the last decade or so by roughly 16%. Considering the ocean between 700 m and the upper limits of our control volumes could add more heat (von Schuckmann et al. 2009; Levitus et al. 2005), reducing the percentage of the contribution computed here somewhat.
The global SLR due to upper-ocean thermal expansion is estimated at about 1.6 (±0.5) mm yr−1 (Bindoff et al. 2007) and the contribution from deep Southern Ocean and global abyssal warming estimated here is about 9% of that rate. This percentage is smaller than the relative contribution to the heat budget because the thermal expansion of seawater relative to its heat capacity is reduced at cold temperatures and deep pressures. While the warming in the global abyssal and deep Southern Ocean only contributes to a fraction of the global SLR budget, the local contribution from deep warming in some regions is similar in magnitude to the global upper-ocean contribution. For instance, in the region south of the SAF, the local SLR estimate due to thermal expansion below 1000 m is greater than 1 mm yr−1 (Fig. 8b). The warming of the deep ocean is contributing to global and local heat and SLR budgets and needs to be considered for accurate assessments of the roles of the ocean in climate change.
Several possible mechanisms could affect the warming reported here, perhaps in combination. First, changes in buoyancy forcing in AABW formation regions could reduce formation rates or change water properties, resulting in local and remote warming (Masuda et al. 2010), possibly over long time scales. This change may be due partly to changes in air–sea heat flux in addition to melting continental ice (Jacobs and Giulivi 2010). Second, long-term intensification and southward movement of westerly winds that drive the ACC appear to result in southward shifts of ACC fronts, also creating warming in the Southern Ocean (Gille 2008; Sokolov and Rintoul 2009), perhaps to great depth as seen here. These stronger winds may also spin up the Weddell gyre, increasing the temperature of abyssal waters escaping that gyre to flow northward (Jullion et al. 2010), and perhaps similarly the Ross gyre. Finally, wind strength and position also affect ice coverage and warm water transport into formation regions, changing formation rates of AABW (Santoso and England 2008).
Abyssal warming in the Southern Ocean is likely to be at least partly caused by advection of warmer water directly from the sources. These basins are located directly downstream from the source regions for AABW and are filled on time scales captured by the data used in this study, as shown by transient tracer burdens (Orsi et al. 1999). Outside of the Southern Ocean, advection times from AABW formation regions to some abyssal locations, such as the North Pacific, can approach 1000 years (Masuda et al. 2010). However, a deep warming signal can propagate from the Southern Ocean to the North Pacific via planetary (Kelvin and Rossby) waves in less than 50 years (Nakano and Suginohara 2002), moving northward on western boundaries, eastward on the equator, poleward at eastern boundaries, and then westward into the interior (Kawase 1987). This remote warming signal could be driven by an increase and southward shift in Southern Ocean westerly winds (Klinger and Cruz 2009) or reductions in buoyancy fluxes near the AABW formation regions that decrease AABW formation rates (Masuda et al. 2010). Alternatively, the more distant changes could also be advective, resulting from changes in AABW formation centuries ago.
The local abyssal heating rates outside of the Southern Ocean (Fig. 8a) are comparable to geothermal heating, typically 0.05 W m−2 away from ridge crests, which can have a significant impact on abyssal ocean circulation and water properties (Joyce et al. 1986; Adcroft et al. 2001). However, if the ocean circulation and geothermal heat fluxes are in steady state, this heating should not cause trends in abyssal temperatures. But, if the abyssal circulation were to slow, geothermal influences might contribute to a change in abyssal temperatures and even circulation.
To gain more precise estimates of the deep ocean's contribution to sea level and global energy budgets, and to understand better how the deep and abyssal warming signals spread from the Southern Ocean around the globe, higher spatial and temporal resolution sampling of the deep ocean is required. The basin space-scale and decadal time-scale resolution of the data used here could be aliased by smaller spatial scales and shorter temporal scales. Furthermore, the propagation of the signal can only be conjectured, not confirmed, with the present observing system.
In summary, we show that the abyssal ocean has warmed significantly from the 1990s to the 2000s (Table 1). This warming does not occur uniformly around the globe but is amplified to the south and fades to the north (Fig. 8). Both Indian and Atlantic oceans only warm on one side, with statistically insignificant cooling on their other side. The recent decadal warming of the abyssal global ocean below 4000 m is equivalent to a global surface energy imbalance of 0.027 (±0.009) W m−2 with Southern Ocean deep warming contributing an additional 0.068 (±0.062)W m−2 from 1000 to 4000 m. The warming contributes about 0.1 mm yr−1 to the global SLR. However, in the Southern Ocean, the warming below 1000 m contributes about 1 mm yr−1 locally. Thus, deep-ocean warming contributions need to be considered in SLR and global energy budgets.
Acknowledgments. Our heartfelt thanks go to all those who helped to collect, calibrate, and process the WOCE and GO-SHIP data analyzed here. Discussions with John Lyman were useful. Comments from Susan Hautala, Takeshi Kawano, Michael Meredith, LuAnne Thompson, Joshua Willis, Carl Wunsch, and two anonymous reviewers improved the manuscript. The findings and conclusions in this article are those of the authors and do not necessarily reflect the views of the National Oceanic and Atmospheric Administration (NOAA). The NOAA Climate Program Office and the NOAA Office of Oceanic and Atmospheric Research supported this research.
Adcroft, A., J. R. Scott, and J. Marotzke, 2001. Impact of geothermal heating on the global ocean circulation. Geophys. Res. Lett., 28, 1735–1738.
Aoki, S., S. R. Rintoul, S. Ushio, S. Watanabe, and N. L. Bindoff, 2005. Freshening of the Adélie Land Bottom Water near 140°E. Geophys. Res. Lett., 32, L23601, doi:10.1029/2005GL024246.
Bindoff, N. L., and Coauthors, 2007. Observations: Oceanic climate change and sea level. Climate Change 2007: The Physical Science Basis. S. Solomon et al., Eds., Cambridge University Press, 385–432.
Boé, J., A. Hall, and X. Qu, 2009. Deep ocean heat uptake as a major source of spread in transient climate change simulations. Geophys. Res. Lett., 36, L22701, doi: 10.1029/2009GL040845.
Böning, C. W., A. Dispert, M. Visbeck, S. R. Rintoul, and F. U. Schwarzkopf, 2008. The response of the Antarctic Circumpolar Current to recent climate change. Nat. Geosci., 1, 864–869.
Cazenave, A., A. Lombard, and W. Llovel, 2008. Present-day sea level rise: A synthesis. C. R. Geosci., 340, 761–770.
Coles, V. J., M. S. McCartney, D. B. Olson, and W. M. Smethie Jr., 1996. Changes in Antarctic Bottom Water properties in the western South Atlantic in the late 1980s. J. Geophys. Res., 101: 8957–8970.
Domingues, C. M., J. A. Church, N. J. White, P. J. Gleckler, S. E. Wijffels, P. M. Barker, and J. R. Dunn. 2008. Improved estimates of upper-ocean warming and multi-decadal sea-level rise. Nature, 453(4), 1090–1093, doi: 10.1038/nature07080.
Fahrbach, E., M. Hoppema, G. Rohardt, M. Schroder, and A. Wisotzki. 2004. Decadal-scale variations of water mass properties in the deep Weddell Sea. Ocean Dyn., 54, 77–91.
Fukasawa, M., H. Freeland, R. Perkin, T. Watanabe, H. Uchida, and A. Nishima. 2004. Bottom water warming in the North Pacific Ocean. Nature, 427, 825–827.
Gille, S. T. 2002. Warming of the Southern Ocean since the 1950s. Science, 295, 1275–1277.
Gouretski, V. V., and K. P. Koltermann. 2004. WOCE global hydrographic climatology. Berichte des Bundesamtes für Seeschifffahrt und Hydrographie Tech. Rep. 35, 52 pp.
Hansen, J., and Coauthors. 2005. Earth's energy imbalance: Confirmation and implications. Science, 308, 1431–1435.
Jacobs, S. S., and C. F. Giulivi. 2010. Large multidecadal salinity trends near the Pacific–Antarctic continental margin. J. Climate, 23, 4508–4524.
Jacobs, S. S., C. F. Giulivi, and P. A. Mele. 2002. Freshening of the Ross Sea during the late 20th century. Science, 297, 386–389.
Johnson, G. C. 2008. Quantifying Antarctic Bottom Water and North Atlantic Deep Water volumes. J. Geophys. Res., 113, C05027, doi:10.1029/2007JC004477.
Johnson, G. C., and S. C. Doney. 2006. Recent western South Atlantic bottom water warming. Geophys. Res. Lett., 33, L14614, doi:10.1029/2006GL026769.
Johnson, G. C., and S. G. Purkey. 2009. Deep Caribbean Sea warming. Deep-Sea Res. I, 56, 827–834, doi:10.1016/j.dsr.2008.12.011.
Johnson, G. C., S. Mecking, B. M. Sloyan, and S. E. Wijffels. 2007. Recent bottom water warming in the Pacific Ocean. J. Climate, 20, 5365–5375.
Johnson, G. C., S. G. Purkey, and J. L. Bullister. 2008a. Warming and freshening in the abyssal southeastern Indian Ocean. J. Climate, 21, 5353–5365.
Johnson, G. C., S. G. Purkey, and J. M. Toole. 2008b. Reduced Antarctic meridional overturning circulation reaches the North Atlantic Ocean. Geophys. Res. Lett., 35, L22601, doi:10.1029/2008GL035619.
Joyce, T. M. 1991. Introduction to the collection of expert reports compiled for the WHP Programme. WHP Operations and Methods–July 1991, WOCE Hydrographic Programme Office Rep., 4 pp. [Available online at http://cchdo.ucsd.edu/manuals/pdf/91_1/introjoy.pdf.]
Joyce, T. M., B. A. Warren, and L. D. Talley. 1986. The geothermal heating of the abyssal subarctic Pacific Ocean. Deep-Sea Res., 33, 1003–1015.
Jullion, L., S. C. Jones, A. C. Naveira Garaboto, and M. P. Meredith. 2010. Wind-controlled export of Antarctic Bottom Water from the Weddell Sea. Geophys. Res. Lett., 37, L09609, doi:10.1029/2010GL042822.
Karstensen, J., P. Schlosser, D. W. R. Wallace, J. L. Bullister, and J. Blindheim. 2005. Water mass transformation in the Greenland Sea during the 1990s. J. Geophys. Res., 110, C07022, doi:10.1029/2004JC002510.
Kawano, T., M. Fukawasa, S. Kouketsu, H. Uchida, T. Doi, I. Kaneko, M. Aoyama, and W. Scheider. 2006. Bottom water warming along the pathways of lower circumpolar deep water in the Pacific Ocean. Geophys. Res. Lett., 33, L23613, doi:10.1029/2006GL027933.
Kawano, T., T. Doi, H. Uchida, S. Kouketsu, M. Fukasawa, Y. Kawai, and K. Katsumata. 2010. Heat content change in the Pacific Ocean between the 1990s and 2000s. Deep-Sea Res. II, 57, 1141–1151, doi:10.1016/j.dsr2.2009.12.003.
Kawase, M. 1987. Establishment of deep ocean circulation driven by deep-water production. J. Phys. Oceanogr., 17, 2294–2317.
Klinger, B. A., and C. Cruz. 2009. Decadal response of global circulation to Southern Ocean zonal wind stress perturbation. J. Phys. Oceanogr., 39, 1888–1904.
Kouketsu, S., M. Fukasawa, I. Kaneko, T. Kawano, H. Uchida, T. Doi, M. Aoyama, and K. Murakami. 2009. Changes in water properties and transports along 24°N in the North Pacific between 1985 and 2005. J. Geophys. Res., 114, C01008, doi:10.1029/2008JC004778.
LeBel, D. A., and Coauthors. 2008. The formation rate of North Atlantic Deep Water and Eighteen Degree Water calculated from CFC-11 inventories observed during WOCE. Deep-Sea Res. I, 55, 891–910.
Levitus, S., J. Antonov, and T. Boyer. 2005. Warming of the world ocean, 1955–2003. Geophys. Res. Lett., 32, L02604, doi:10.1029/2004GL021592.
Lumpkin, R., and K. Speer. 2007. Global ocean meridional overturning. J. Phys. Oceanogr., 37, 2550–2562.
Lyman, J. M., S. A. Good, V. V. Gouretski, M. Ishii, G. C. Johnson, M. D. Palmer, D. M. Smith, and J. K. Willis. 2010. Robust warming of the global upper ocean. Nature, 465, 334–337, doi:10.1038/nature09043.
Masuda, S., and Coauthors. 2010. Simulated rapid warming of abyssal North Pacific water. Science, 329, 319–322, doi:10.1126/science.1188703.
Meehl, G. A., W. M. Washington, W. D. Collins, J. M. Arblaster, A. Hu, L. E. Budja, W. G. Strand, and H. Teng. 2005. How much more global warming and sea level rise? Science, 307, 1769–1772.
Meredith, M. P., A. C. Naveira Garabato, A. L. Gordon, and G. C. Johnson. 2008. Evolution of the deep and bottom water of the Scotia Sea, Southern Ocean, during 1995–2005. J. Climate, 21, 3327–3343.
Miller, L., and B. C. Douglas. 2004. Mass and volume contributions to twentieth-century global sea level rise. Nature, 248, 406–409.
Murphy, D. M., S. Solomon, R. W. Portmann, K. H. Rosenlof, P. M. Forster, and T. Wong. 2009. An observationally based energy balance for the Earth since 1950. J. Geophys. Res., 114, D17107, doi:10.1029/2009JD012105.
Nakano, H., and N. Suginohara. 2002. Importance of the eastern Indian Ocean for the abyssal Pacific. J. Geophys. Res., 107, 3219, doi:10.1029/2001JC001065.
Orsi, A. H., T. Whitworth, III, and W. D. Nowlin, Jr. 1995. On the meridional extent and fronts of the Antarctic Circumpolar Current. Deep-Sea Res. I, 42, 641–673.
Orsi, A. H., G. C. Johnson, and J. L. Bullister. 1999. Circulation, mixing, and production of Antarctic Bottom Water. Prog. Oceanogr., 43, 55–109.
Osterhus, S., and T. Gammelsrod. 1999. The abyss of the Nordic seas is warming. J. Climate, 12, 3297–3304.
Ozaki, H., H. Obata, M. Naganobu, and T. Gamo. 2009. Long-term bottom water warming in the North Ross Sea. J. Oceanogr., 65, 235–244.
Raper, S. C. B., and R. J. Braithwaite. 2006. Low sea level rise projections from mountain glaciers and icecaps under global warming. Nature, 439, 311–313.
Raper, S. C. B., J. M. Gregory, and R. J. Stouffer. 2002. The role of climate sensitivity and ocean heat uptake on AOGCM transient temperature response. J. Climate, 15, 124–130.
Rintoul, S. R. 2007. Rapid freshening of Antarctic Bottom Water formed in the Indian and Pacific Oceans. Geophys. Res. Lett., 34, L06606, doi:10.1029/2006GL028550.
Roemmich, D., J. Gilson, R. Davis, P. Sutton, S. Wijffels, and S. Riser. 2007. Decadal spinup of the South Pacific subtropical gyre. J. Phys. Oceanogr., 37, 162–173.
Santoso, A., and M. H. England. 2008. Antarctic Bottom Water variability in a coupled climate model. J. Phys. Oceanogr., 38, 1870–1893.
Smith, W. H. F., and D. T. Sandwell. 1997. Global seafloor topography from satellite altimetry and ship depth soundings. Science, 277, 1956–1962.
Sokolov, S., and S. R. Rintoul. 2009. Circumpolar structure and distribution of the Antarctic Circumpolar Current fronts: 2. Variability and relationship to sea surface height. J. Geophys. Res., 114, C11019, doi:10.1029/2008JC005248.
Solomon, S., D. Qin, M. Manning, Z. Chen, M. Marquis, K. B. Averyt, M. Tignor and H. L. Miller, Eds. 2007. Climate Change 2007: The Physical Science Basis. Cambridge University Press, 996 pp.
Trenberth, K. E., and J. T. Fasullo. 2009. Changes in the flow of energy through the Earth's climate system. Meteor. Z., 18, 369–377.
von Schuckmann, K., F. Gaillard, and P.-Y. Le Traon. 2009. Global hydrographic variability patterns during 2003–2008. J. Geophys. Res., 114, C09007, doi:10.1029/2008JC005237.
Warren, B. A., and K. G. Speer. 1991. Deep circulation in the eastern South Atlantic Ocean. Deep-Sea Res., 38, (Suppl.), 281–322.
Willis, J. K., D. P. Chambers, and R. S. Nerem. 2008. Assessing the globally averaged sea level budget on seasonal to interannual timescales. J. Geophys. Res., 113, C06015, doi:10.1029/2007JC004517.
Yashayaev, I., and A. Clarke. 2008. Evolution of North Atlantic water masses inferred from Labrador Sea salinity series. Oceanography, 21, 30–45.
Zenk, W., and E. Morozov. 2007. Decadal warming of the coldest Antarctic Bottom Water flow through the Vema Channel. Geophys. Res. Lett., 34, L14607, doi:10.1029/2007GL030340.
Go to Next section