We interpolate data for each occupation of the 28 studied sections onto closely spaced vertical and horizontal grids along their tracklines for analysis. First, potential temperature (θ) is derived from the 2-dbar CTD data at each station. The station θ profiles are then low passed vertically with a 40-dbar half-width Hanning filter and interpolated onto a 20-dbar vertical grid. At each pressure, the data are then interpolated onto an evenly spaced standard 2′ longitudinal or latitudinal grid along the section trackline using a space-preserving piecewise cubic Hermite interpolant. The horizontal grid chosen matches a 2′ bathymetric dataset derived from merging satellite altimetry data and bathymetric soundings (Smith and Sandwell 1997). The bathymetric dataset and the measured CTD maximum pressures for each station are used to mask interpolated data located below the sea floor. In addition, interpolated data are discarded between any gaps in station spacing exceeding 2° of latitude or longitude along a trackline.
We calculate a rate of change in θ with time (dθ/dt) at every vertical and horizontal grid point along each trackline using data from all occupations of that section where the time between the first and last occupation exceeds 2.5 yr. In places with only two occupations, dθ/dt is calculated by dividing the θ change between occupations by the time between occupations. For sections with more than two occupations, at each grid point a line is fit to θ data versus time using least squares, allowing estimates of both dθ/dt and its uncertainty from the slope of the line and its error (Fig. 3). Here we assume that errors owing to spatial and temporal variability discussed immediately below dominate and ignore slope uncertainties and the comparatively small instrumental errors of 0.001°–0.002°C. We construct pressure–latitude or pressure–longitude sections of dθ/dt estimates for each repeat section (e.g., Fig. 4). Generally, sections with three or more occupations evince amonotonic temperature trend with time on basin scales. For instance, the warming rates in the southwest Pacific basin among the three distinct pairs formed by the three occupations of P06 (a trans-Pacific section along 32°S, Fig. 1) are grossly similar (Fig. 5). While there is variability among the three rate estimates at any given depth and the estimate over the longest time interval is smoothest in the vertical, using any two of the three occupations would result in a similar depth-averaged rate of abyssal warming.
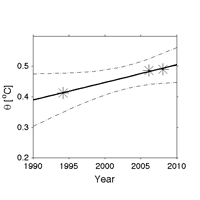
Fig. 3. Local dθ/dt estimate for a location with more than two section occupations. Potential temperature data (asterisks) from three occupations along P18 (see Fig. 4, green asterisk, for location) at 56°S and 4000 dbar plotted vs time are used to fit a line by least squares (solid line), producing an error estimate here shown at 95% confidence limits (dotted line). The slope of the line is dθ/dt.
Fig. 4. Time rate of change of potential temperature dθ/dt (color bar), along the trackline of P18 (see Fig. 1 for location). Areas of warming are shaded in red, and regions of cooling are shaded in blue with intensity scaled by the magnitude of the change. Mean θ values over all occupations are contoured (black lines). This trackline is grouped into four basins for analysis (boundaries shown by vertical black lines), and the area south of the SAF (vertical dotted–dashed line) is also analyzed separately. The basins from south to north are the Amundsen–Bellingshausen Basin, Chile Basin, Peru Basin, and central Pacific Basin. Green asterisk denotes location of data used in Fig. 3.
Fig. 5. Mean time rate of change in potential temperature dθ/dt at each pressure along the portion of P06 crossing the southwest Pacific basin (Fig. 1) calculated using every combination of pairs of the three occupations of P06 (see legend).
The dθ/dt contours along section tracklines reveal vertically banded structures extending throughout the water column (Fig. 4). These vertical structures are most likely due to mesoscale ocean eddies, internal waves, and tides that cause vertical displacements of isopycnals. To evaluate the statistical significance of large-scale dθ/dt patterns observed in the face of such variations, a robust estimate of a characteristic horizontal decorrelation length scale is required to calculate the effective degrees of freedom (DOF). To evaluate the length scale of these features, at every pressure level along each trackline, we remove unsampled (masked) grid points, and then find the maximum of the integral of the spatially lagged autocovariance of the spatially detrended warming rate, following Johnson et al. 2008a. Twice this integral gives an estimate of the horizontal decorrelation length scale.
The horizontal decorrelation length scale varies among sections, with values ranging from 25 to 400 km, but generally clustering near 160 km (Fig. 6). The decorrelation length scales estimated from each section are relatively constant vertically from about 500 to 5000 dbar because energetic vertical features in dθ/dt tend to be coherent throughout the water column. Deeper than 5000 dbar the length scale gradually tends toward zero with depth, as the sampled region gets smaller and smaller, and there are more breaks in the sections owing to intervening topography. Shallower than 500 dbar, the length scales sometimes get longer, perhaps owing to large-scale wind-driven shifts in gyre positions or aliasing of the seasonal cycle. At each pressure surface, using repeat sections with lengths greater than 2000 km, we calculate the median of the horizontal decorrelation length scale (Fig. 6). There are 25 sections longer than 2000 km at the surface, but this number decreases with depth to only 11 sections by 5000 dbar. Between 500 and 5000 dbar, the median is fairly constant around 163 km. The vertical mean and median of the median between 500 and 5000 dbar are both 163 km. This value is used throughout this study as our best estimate of the horizontal length scale for all sections at all pressures. We chose the 2000-km section-length criterion based on an examination of decorrelation-length scale estimates versus section length (not shown). For sections longer than 2000 km the decorrelation-length scale estimates asymptotically approach a common value. The criterion chosen ensures the sections used for the decorrelation-length scale estimate sample this length scale roughly a dozen times or more.
Fig. 6. Horizontal decorrelation length scales (km) of dθ/dt for each of the 28 repeat sections (gray lines) calculated at each pressure. The median (thick black line) and quartiles (thin black lines) are calculated from all sections with horizontal lengths greater than 2000 km at a given pressure. The pressure-averaged mean and median of the median length scale from 500 to 5000 dbar is 163 km.
For this analysis we divide the ocean into 32 deep basins (Fig. 1) based on bottom topography (Smith and Sandwell 1997) and climatological ocean bottom temperature (Gouretski and Koltermann 2004). The boundaries for the basins follow the major ocean ridges, most of which are shallower than 3000 m. Most of the 32 deep basins were crossed by at least one section, with the exception of the Arabian Sea and Somali Basin in the northwest Indian Ocean (Fig. 1). A few marginal seas (the Sea of Okhotsk, Sea of Japan, Philippine Sea, Guatemala Basin, Panama Basin, and Gulf of Mexico) are also unsampled, but these are all mostly shallower than 4000 dbar, and thus have a minor impact on our study. The Arctic Ocean and Nordic seas, which contain little or no AABW, were not sampled by the available repeat sections analyzed here, and thus are not included in this study.
We estimate a mean warming rate and its associated uncertainty at each pressure horizon for each of the 24 deep basins sampled (e.g., Fig. 7). For these estimates, we divide the sections at the basin boundaries and calculate the mean and standard deviations of the warming rates on isobars within each basin. If a basin only has one section crossing it, the means and standard deviations for the single section within the basin as a function of pressure are assumed to be representative of the whole basin. If a basin is crossed by more than one section, the length-weighted means and standard deviations are calculated using data fromportions of all sections crossing that basin at each pressure level. For example, the mean du/dt for the Amundsen–Bellingshausen Basin of the southeast Pacific (Fig. 7) estimates warming of about 0.002°C yr−1, statistically different from zero at 97.5% confidence below about 3500 m. This result might be anticipated from examination of the warming rate along the P18 section (Fig. 4), which is the major contributor to this estimate, augmented only by a small portion of the southern end of P16 that also enters the basin (Fig. 1). We discuss the assumption that the length-weighted temperature trend statistics for the repeat hydrographic section tracklines crossing each basin are representative of the entire basin further in section 5.
Fig. 7. Mean (thick black line) and 95% confidence limits (thin black lines) of dθ/dt for the Amundsen–Bellingshausen Basin calculated as described in the text, a length-weighted combination of the portions of repeated sections that cross the basin (in this instance P18 and P16, see Fig. 1 for locations).
At each pressure level we compute the DOF for each section crossing the basin by dividing the horizontal length of the section at that pressure by the single horizontal decorrelation length scale of 163 km. In areas where topography isolates the sampled regions such that one region is continuously sampled in the horizontal over a distance less than the decorrelation length scale, and that region is separated from adjacent sampled regions by distances more than the decorrelation length scale, the data from the region in question are assumed to be statistically independent and to contribute one DOF to the estimate. The DOF at each pressure within each basin is the sum of the DOF for all sections that cross that basin. The standard deviation is converted to a standard error by dividing by the square root of the DOF, and the two-sided 95% confidence interval is estimated assuming a Student's t distribution.
In each basin where measurements do not extend to the deepest portions of that basin, the deepest estimate of dθ/dt is applied to the deep unsampled portions of that basin. Prior to this operation, each basin is visually inspected to make sure that the deepest estimate is well below the sill depth of that basin and that the volume of water below the deepest estimate is small compared to the volume of the basin.4000 m. If these conditions are not met, the extension is not applied.
In addition to these basin-based warming estimates using physical topographical boundaries, we make one other estimate of du/dt for the entire Southern Ocean. We use an estimate of the location of the SAF (Orsi et al. 1995), which demarks the northern edge of the ACC, as the northern boundary for the region. Even though it is not a physical boundary, the SAF acts as a dynamical boundary separating water masses. While the SAF moves in time and has trended south slightly over recent decades (Gille 2008; Sokolov and Rintoul 2009), a time-invariant control volume is required for heat and sea level budgets, so motions of the SAF are not considered in this analysis. South of the SAF, isotherms rise steeply, indicating that the cold dense water of Antarctic origins found only in very deep regions to the north of the SAF extends to shallower ranges of the water column to the south of the SAF (Figs. 1b and 4). The eight meridional and one zonal section that sample regions south of the SAF (Fig. 1b) are grouped together to estimate the warming rate along pressure horizons in the Southern Ocean. The meridional sections are reasonably evenly spaced around the globe and give good coverage of the south Indian and South Atlantic oceans. However, there is only one section in the South Pacific Ocean (P18, located on the eastern side, see Fig. 1) that approaches even the base of the Antarctic continental rise, so this region is underrepresented in the final estimates of Southern Ocean changes.
The warming rate of the entire Southern Ocean south of the SAF is estimated at each pressure. Using the same method described above for basins with multiple crossings, the nine sections with data south of the SAF (Fig. 1b) are used to find the length-weighted means and 95% confidence intervals of the warming rate in the Southern Ocean. As mentioned above, owing to the spatial distribution of available data, these values are somewhat biased toward θ changes in the south Indian and South Atlantic oceans over the South Pacific Ocean and thus might be more representative of property changes originating from Weddell Sea or Adelie Land Bottom Water rather than those originating from Ross Sea Bottom Water. In addition, since not all the tracklines extend to the Antarctic continental rise (Fig. 1b), the northern portions of the Southern Ocean may also be overrepresented in the warming rates for the Southern Ocean presented here.
Return to Abstract
Return to Previous section
Go to Next section