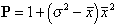(1)U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
Lloyd's (1967) index of patchiness is often used to quantify the degree of patchiness in ichthyoplankton distributions (Frank et al., 1993; Hewitt, 1981; Houde and Lovdal, 1985; Matsuura and Hewitt, 1995). It is the ratio of mean crowding of a population to its mean density. The mean crowding is defined as the mean number of neighbors per individual per unit area. Individuals are neighbors if they are taken in the same sample.
A patchiness index that is not a function of the population density is ideal because it permits comparisons of patchiness between years with varying abundance and over different life stages. Since the mean crowding is averaged over individuals, it is unaffected by samples taken outside the natural range of the organism which contain no individuals. However, the mean population density would be reduced with these zero-count samples included. Therefore the patchiness index would rise. For example, if the domain consists of the Gulf of Alaska, then each aggregation of spawning pollock (e.g. Shelikof Strait, Shumagin Islands, Chirikof Island) appears as a patch. On this scale, Lloyd's index of patchiness would be large. We focussed on pollock spawning in Shelikof Strait since our interests are the processes in this smaller domain. Lloyd's index is independent of the sampling domain on this scale. We defined the spatial extent of our domain by excluding all stations with zero-counts of pollock eggs or larvae at the edge of the domain. Zero-count stations within this domain were retained since they contribute legitimately to the patchiness.
The area sampled should be much smaller than the size of the patches but large enough so that the relative space occupied by the individual organisms is negligible (Lloyd, 1967). In theory, the minimum observable patch size would be that of a single bongo tow, or a diameter of ~1 km. Survey design, however, dictates the actual minimum and maximum scales. The former is station spacing, generally >10 km, and the latter is geographic range of the survey. The coarseness of the sampling grid did not permit resolution of the scales of patches using either correlograms or variograms (Rossi et al. 1992; P. Dell'Arciprete, Fisheries Research Institute, Univ. Washington, pers. comm.). Examination of maps of larval concentrations suggested, however, that patches occur on scales of 10-50 km.
Lloyd's index (1967) is given by
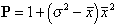(1)
where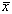 
is the population
mean density of eggs or larvae per 10 m2 and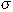 
2 is the population variance. As in most
experiments, the true population mean and variance are unknown, and only their
sample estimates are available from observations. Unfortunately, substitution
of the sample estimates into eqn (1) gives a value of P for
which the standard error cannot be reliably calculated. Instead many investigators
fit a negative binomial distribution to the frequency distribution of population
density samples. Such a fit gives the maximum likelihood estimator (Bliss
and Fisher, 1953), k, that relates the variance to the mean by
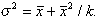(2)
The standard error of the patchiness can be derived following Lloyd (1967)
Std error (P) = (var(k))½/k2 (3)
where var(k) is the sampling variance for k. P equals unity for a random distribution and increases without bound for increasingly aggregated populations.
We first calculated P for eggs and larvae (regardless of age) for each cruise. Lloyd's index for eggs was nearly constant (3.6-6.1) with a small standard error (Table 1; Fig. 2). For larvae, the variability in P was much larger (3.9-16.2; Table 2), as was the standard error. Values of P were greatest and most variable shortly after hatching; both the magnitude and variability decreased during the early larval period. Starting from the middle of larval stage (~12 mm), Lloyd's index increased again. This is similar to the U-shaped pattern for larvae described by others. These results substantiate previous work based on two years of larval data (Kim, 1987) and extend the analysis through the early juvenile stage. A primitive equation, hydrodynamic model was used to simulate advection of larvae and the ensuing distributions were used to obtain estimates of P (Hermann et al., 1996a, see pp. 39-57 in this supplement). The age-dependent pattern of these model estimates between newly hatched and late larval stages was similar to ours (Fig. 2). Since no schooling behavior was included in the model, however, patchiness in the simulations remained low through the juvenile period.
Figure 2. Estimates of Lloyd's index of patchiness for eggs (solid box) and larvae (open circle). Results from a given survey, regardless of egg or larval size (age), are shown as a function of the mean survey date. The error bars show the standard error of the index estimates. The heavy line shows the mean index for larvae from model results (Hermann et al., 1996a).
The trends in the estimates of P suggest that a relationship exists between patchiness and larval age. To explore this, we calculated P as a function of size class (closely correlated with age). This analysis also removed any bias toward younger animals whose numbers had not been reduced by mortality. The largest P occurred for newly hatched larvae, and a minimum occurred between 8 and 14 mm, or ~42 days post-hatch (Fig. 3). As the pollock entered late larval or early juvenile stage, patchiness increased. Patchiness for eggs was not significantly dependent upon stage.
Figure 3. Lloyd's index of patchiness as a function of egg stages and larval length (age). Age was estimated using results from Bailey et al. (1996). Larvae were grouped by 2-mm bins for lengths <17 mm and by 8-mm bins for larger animals. Data sets that consisted of >90% zeros were not used. A line connects the mean values of P for each stage (eggs) and for each length bin (larvae).
Lloyd's index provides no information regarding the percentage of larvae occurring in patches. To obtain an estimate of the contribution of larvae in patches to the total population, we computed the proportion of larvae present at stations where the larval concentration (number/10 m2) exceeded the survey mean by one standard deviation. Almost 92% of the larvae were found in a patch near Cape Kekurnoi during April 1981 (2SH81; Fig. 4e) and only 30% occurred in a patch located northeast of Sutwik Island in May of 1988 (4MF88A; Fig. 4b). Not surprisingly, the percent of larvae in patches was well correlated with Lloyd's index (r = 0.84).
Figure 4. Contours of pollock larvae in Shelikof Strait. The three types of distributions are shown in panels: (a) transient event [1MF88], (b) and (c) Sutwik Island [4MF88A and 4MF89], and (d) eddy, 2MF90 (dotted line shows the 2,250 larvae/10 m2 contour). Panel (e) shows contours from the survey with the greatest abundance [2SH81] and an example of a high Lloyd's Index [P = 16.1]. Panel (f) shows a distribution with a low patchiness [P = 5.2; 3MF91]. Contour intervals are 10, 50, 100, 500, 1000, 5000, 10,000 and 50,000 larvae/10 m2.
Return to previous section or go to next section
