U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
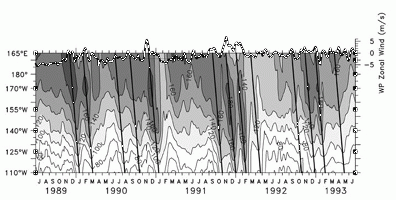
The intraseasonal Kelvin waves are clearly seen as sloped bands of high and
low values in the longitude-time plot of 20°C depth along the equator (Figure
3). We show the 4-year period from mid 1989 to mid 1993 because there were
sufficient buoys to reliably perform the zonal interpolation and because the
waves were relatively well developed at this time. The previous
Figure 3. Longitude-time plot of 20°C depth on the equator. The contours and shading show the depth of the 20°C isotherm, zonally interpolated between the buoy positions (see text). Contour interval is 20 m, and deeper thermocline depths are darker shades. The slanted lines show identified downwelling Kelvin wave ray paths (see text) and represent a speed of 2.4 m s-1. The heavy line at top shows the time series of zonal winds averaged over 165°E-180° (scale at upper right). Both time series have been smoothed with a 17-day triangle filter (see text).
Observed changes to the mean thermocline slope and depth during the
It is clear from Figure 3 that the intraseasonal
Kelvin waves form a major component of equatorial thermocline depth variability.
Slanted lines have been overplotted to show the downwelling waves; their slope
represents a speed of ![]() = cT gives
= cT gives ![]()
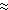
There is a close visual coherence between zonal winds over the far western
Pacific (heavy line at the top of Figure 3) and
thermocline depth in the east/central Pacific. Figure
3 shows that virtually every western Pacific wind fluctuation was reproduced
in 20°C depth signals propagating across the basin at Kelvin-like speeds of
2 to 3 m s-1. The correlation of zonal winds at 165°E with 20°C depth
at 140°W was greater than 0.7 at a lag of
The corresponding longitude-time plot of surface zonal winds along the equator (Figure 4) suggests that the zonal wind has a shorter zonal coherence scale than either 20°C depth or SST. Typically the strongest trades in the central Pacific occur during boreal fall/winter, which is when westerly events are most prominent in the far west. This out-of-phase relation between central and western Pacific is associated with the westward propagation of the annual cycle of zonal winds across the basin [e.g., Meyers, 1979; Lukas and Firing, 1985; Gent, 1985; Kessler and McCreary, 1993]. The result is that the correlation of winds along the equator has a relatively short zonal scale and becomes negative after a few thousand kilometers. The short zonal scales are consistent with those observed for deep tropical convection [Waliser et al., 1993].
Figure 4. Longitude-time plot of zonal winds on the equator. The plot has the same format as Figure 3 for 20°C depth. The contours and shading show the zonal wind at a contour interval of 3 m s-1. Westerlies are darker shades. The heavy curve at top show the time series of OLR averaged between 160°E and 170°E on the equator, with values below 220 W m-2 darkened (scale at upper right). Both time series have been smoothed with a 17-day triangle filter.
Western Pacific westerly winds often appear as a series of roughly month-long
events, rather than a simple annual sinusoid (Figure
4). Unlike 20°C depth (Figure 3) there is
only weak evidence of eastward propagation of the individual intraseasonal wind
events, but successive events often extend farther to the east than did the
preceding one. The 1991-1992 El Niño is evident in the zonal wind time series
as a stronger-than-usual period of westerly events, which extended further east
than in the preceding years (Figure 4). This
low-frequency signal was disrupted by the intraseasonal waves, and between the
strong westerly events the western Pacific winds returned to more normal conditions
with easterlies or very weak westerlies (Figure 4).
With the first of the series of MJOs in September 1991, substantial weakening
of the trades west of about 170°W was observed (Figure
4). The "collapse of the trades" occurred during January 1992,
when westerly winds were seen as far east as 140°W for about
The occurrence of western Pacific westerly events corresponded closely to low
values of OLR, which indicate the presence of intense tropical convection (heavy
line at the top of Figure 4). At 0°, 165°E, the
largest lag correlation of zonal winds and OLR was 0.7, with OLR leading the
winds by about
The corresponding longitude-time plot of sea surface temperature (SST) along
the equator (Figure 5) shows a very different
character of variability. Whereas thermocline depth and western Pacific zonal
winds demonstrated large-amplitude intraseasonal fluctuations, SST variations
were largely of lower frequency. An annual cycle was prominent east of about
170°W, and in the eastern Pacific the annual occurrence of warm SSTs lagged
the deepest thermocline (Figure 3) by 2-3 months.
During the ENSO warm event of 1991-1992 the 29°C isotherm moved east from its
usual position near the date line to about 140°W, and maximum SST at 110°W reached
28°C, about 1°-2°C warmer than the annual maxima of the previous 2 years. Before
the 1991-1992 event, in 1989 and 1990 the cold tongue (defined roughly as the
SST less than 25°C) persisted through January of the following year east of
140°W. However, in September-October 1991 a relatively abrupt warming took place
across the basin, which roughly coincided with the first of the four downwelling
Kelvin waves of this event and terminated the annual cold period about 3 months
earlier than usual (Figure 5). While the SST
was warming to its peak in the eastern Pacific during March 1992, the western
Pacific at 165°E cooled below 29°C for the first time since 1989. Superimposed
on these low-frequency changes of SST in Figure 5
are 500-
Figure 5. Longitude-time plot of SST on the equator. The plot has the same format as Figures 3 and 4. The contours and shading show the SST (actually, the 1-m temperature) at a contour resolution of 1°C, with supplementary shading at 29.5°C. Darker shades show warmer SST. The slanted lines are the same Kelvin wave paths shown in Figure 3.
Spectra of OLR and zonal winds in the western Pacific, and 20°C depth and zonal
current at the undercurrent level in the central Pacific are shown in Figure
6. The spectra were calculated for the 10-year period April 1983-April 1993
for all quantities except the zonal wind, for which only the seven years July
1986-July 1993 are available. The spectra were estimated from the raw periodogram
amplitudes by smoothing in six frequency bands, with breaks at 600-, 225-, 110-,
45-, and 20-day periods, corresponding roughly to interannual, annual, semiannual,
intraseasonal, monthly and submonthly variability. Within each of these bands
the periodogram estimates were smoothed with a triangle filter whose length
was constant within the band; however, a longer filter length was used to give
greater smoothing in the higher-frequency bands. The resulting degrees of freedom
(DF) were estimated according to the procedure of Bloomfield
[1976, Chapter 8]; these range from 5 DF in the interannual band, to about
20 DF in the intraseasonal band and to about 60 DF for periods less than
Figure 6. Variance-preserving spectra of OLR at 165°E, zonal wind at 165°E, 20°C depth at 140°W, and equatorial undercurrent speed at 140°W, 120 m depth, all at the equator. Each variable has a separate scale as indicated. The spectra are calculated for the 10-year period April 1983-April 1993 for all quantities except the zonal wind, for which only the 7 years July 1986-July 1993 are available.
The spectra given in Figure 6 show that the intraseasonal band was a prominent feature of the variability of all these quantities, as expected from previous results and the plots discussed in section 3.1. The longitudes chosen for Figure 6 are roughly at the maximum amplitude of intraseasonal variability for OLR and 20°C depth; in the case of zonal wind this amplitude increased toward the west and may have been larger to the west of 165°E. The amplitude of zonal winds and OLR in this band dropped off rapidly east of the date line, so much of the oceanic intraseasonal variability in the eastern Pacific must have been remotely forced. The intraseasonal band variability in the atmospheric quantities shown (OLR and zonal wind) was skewed toward the high-frequency end of the band near 45-day or shorter periods, while the oceanic variability (20°C depth and undercurrent speed) peaked near 60- to 75-day or longer periods (Figure 6). There was little oceanic energy in the central Pacific at periods shorter than 50 days, even though there was such energy in OLR and the wind forcing. This discrepancy is reflected in the fact that many of the papers discussing intraseasonal variability in the atmosphere refer to "30-60 day" or "40-50 day" fluctuations [e.g., Madden and Julian, 1972; Weickmann et al., 1985; Lau and Chan, 1985, 1986; Zhu and Wang, 1993], but the ocean seems to selectively respond to the lower-frequency part of the intraseasonal forcing. We discuss this question further in section 4.6.
In addition to the intraseasonal peak, major spectral peaks are also seen at
3- to 4-year periods associated with the ENSO cycle, and at the annual period
(Figure 6). Weak semiannual variability was indicated
for all four quantities, with only slightly higher energy levels than neighboring
frequencies. It is noteworthy, but beyond the scope of this paper, that although
there have been large changes, even reversals, of the equatorial undercurrent
in the central Pacific associated with El Niño [e.g.,
Firing et al., 1983; Halpern,
1987], these events were short lived and did not compose a very large fraction
of the variance, so there was no interannual spectral peak of zonal current
at
All four quantities shown in Figure 6 were coherent
at periods longer than 1 or
Figure 7. Squared coherence amplitude of OLR at 165°E, zonal wind at 165°E and zonal current at 140°W with 20°C depth at 140°W; 95% confidence levels are indicated by the thin horizontal lines, which also show the frequency bands used to smooth the raw periodograms (see text).
The intraseasonal coherence among OLR, west Pacific winds and central Pacific
thermocline is not surprising, but it is important because the OLR events are
known to propagate eastward into the Pacific from the Indian Ocean as part of
the Madden-Julian Oscillation [Weickmann
et al., 1985; Rui
and Wang, 1990]. The Indian-Pacific connection is shown by high coherence
in the intraseasonal band between OLR at 90°E in the eastern Indian Ocean and
20°C depth at 140°W,
Figure 8. Squared coherence amplitude (top) and phase (bottom) of OLR at 90°E with 20°C depth at 140°W. The intraseasonal peak is centered at 74 days. Positive phase indicates deep 20°C depth leads low OLR. (Top) 95% confidence limits on the coherence amplitude are shown by the thin horizontal lines; 95% confidence limits on the phase are shown as "error bars," in each of the five frequency intervals in which the coherence (top panel) is significant above the 95% level. The phase limits are an average over each such interval and are plotted at the center of the intervals.
The Pacific Ocean Kelvin wave speed itself is found from Figure
9, which shows the squared coherence amplitude and phase of 20°C depth across
the equatorial band, averaged over periods of 55-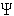 n(z) [Cane,
1984; Kessler
and McPhaden, 1995a]. When these quantities are calculated from the
mean historical profiles at different locations along the equator in the Pacific,
it is found that the first-mode speed c1 varies only from
about
n(z) [Cane,
1984; Kessler
and McPhaden, 1995a]. When these quantities are calculated from the
mean historical profiles at different locations along the equator in the Pacific,
it is found that the first-mode speed c1 varies only from
about 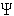 n(z)
show considerably more zonal variation, which might be expected to result in
wave reflections and interactions between modes [Gill
and King, 1985; Long
and Chang, 1990]. One can interpret the nearly constant phase speed
in a reduced gravity representation (where the phase speed is c2
= g(
n(z)
show considerably more zonal variation, which might be expected to result in
wave reflections and interactions between modes [Gill
and King, 1985; Long
and Chang, 1990]. One can interpret the nearly constant phase speed
in a reduced gravity representation (where the phase speed is c2
= g(![]()
 /
/ )H,
with
)H,
with ![]()
 the density contrast across the interface and H the mean interface depth).
Although the thermocline shoals in the east, the vertical density contrast increases
in the cold tongue region, and the two compensate to produce a net change in
c that is less than would occur due to thermocline depth variations alone.
the density contrast across the interface and H the mean interface depth).
Although the thermocline shoals in the east, the vertical density contrast increases
in the cold tongue region, and the two compensate to produce a net change in
c that is less than would occur due to thermocline depth variations alone.
Figure 9. Squared coherence amplitude and phase of 20°C depth over the zonal extent of the buoy array with that at 140°W, averaged in the frequency band 55-65 days. The solid line shows the coherence amplitude (identically 1 at 140°W), and the light dashed horizontal line is the 95% confidence level (scale at left). The heavy dashed line is the phase, expressed as a lag in days with the phase at 140°W (scale at right). The thin solid line along the phase is a best fit straight line to the phase and represents a speed of 2.43 m s-1. This fit is the basis for the slope of the slant lines in Figures 3 and 5.
The spectral representations shown in Figures 6,
7, 8, and 9
depict the average variability over the whole record lengths. Complex demodulation
is a simple technique that gives time series of the amplitude and phase of the
variability within a frequency band (see section 2.1) and thus allows examination
of the temporal modulation of energy content of a particular band. Demodulation
of the time series of 20°C depth at 140°W, at a central period of
Figure 10. Time-varying amplitude of the intraseasonal variability obtained through complex demodulation of (a) 20°C depth at 0°, 140°W, (b) zonal winds at 165°E, and (c) OLR at 165°E. The demodulation is performed about a central frequency of 60 days, with half-power between 42 and 108 days. The dashed line overlaid is a 1-year running mean of each demodulated time series.
Figure 11. Average year of 60-day amplitude of 20°C depth at 0°, 140°W (meters, solid line, scale at left; data from Figure 10a), zonal winds at 165°E (meters per second, dashed line, scale at right; data from Figure 10b) and OLR at 165°E (W m-2, dotted line, scale at left; data from Figure 10c).
In late 1988 a sharp peak of 60-day amplitude occurred that did not represent the usual annual downwelling Kelvin waves associated with MJO convection and westerlies in the western Pacific, despite the fact that it appears to fit the annual pattern of maxima (Figure 10a). Instead, this event was a strong upwelling signal that was generated by a fairly confined patch of easterly winds near the date line [Picaut and Delcroix, 1995] and marked the maximum cooling of the La Niña of 1988 (Figure 2). If we omit the non-MJO 1988 peak, the largest intraseasonal signals of 20°C depth are found at the beginnings of 1987 and 1992 (Figure 10a), both associated with the El Niño events of those years, and these appear as enhancements of the deep-thermocline phase of the annual cycle.
The corresponding demodulation of zonal wind at 165°E is shown in Figure
10b. As in the case of 20°C depth, a strong annual signal of 60-day variability
is seen, with peaks roughly 3 times larger than the background occurring at
the end of each year. The average annual and semiannual variation of 60-day
wind amplitude (Figure 11) is very similar to
that for 20°C depth, with the western Pacific winds leading 140°W 20°C depth
by
The corresponding demodulation of the OLR time history averaged over 160°-170°E
on the equator is shown in Figure 10c. Again,
for most years the OLR intraseasonal variability peaked in boreal fall/winter
with an amplitude 2 to 3 times the background. The average year of OLR 60-day
amplitude (Figure 11) shows peak amplitude in
February-March,
Return to previous section or go to next section