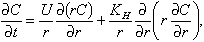(4)U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
We believe that the increased patchiness in the late larval and early juvenile stages resulted from an increasing ability of these animals to swim and respond to their environment (Olla et al., 1996, see pp. 167-178 in this supplement). With time, diffusion tends to equalize the concentration of larvae over space. Larvae could balance this effect by actively swimming toward the center of the patch. To evaluate this possibility, we considered an idealized analytical model of a larval patch. In polar coordinates, the change in concentration (C) of larvae with time (t) in an axisymmetric patch of constant radius is given by the advection-diffusion equation
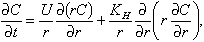(4)
where r is the distance of the larvae from the center of the patch, U is the assumed constant larval swimming speed (toward the center of the patch), and KH the horizontal eddy diffusivity. Equation 4 allows a bounded steady state solution:
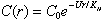(5)
where C0 is the concentration at the patch center. For
a wide range of oceanic scales and in the absence of horizontal shear, experiments
show that the eddy diffusivity coefficient can be approximated by 2 × 10-3 R4/3 cm2
s-1, where R is the radius of the patch (Okubo,
1980). From eqn (5), the radial swimming speed (U) required to
maintain a portion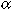 
of larvae within
a circle of radius R is
U = -2 × 10-3 ln(1 - 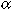) R1/3
(6)
and for 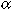= 0.99,
U = 9.2 × 10-3 R1/3.
The greatest change of patch radius with swimming speed occurs for U < 0.7 cm s-1 (Fig. 6). For a patch with radius comparable to observed eddies in Shelikof sea valley (~15 km), a minimum radial swimming speed of 1.0 cm s-1 would be required to maintain a patch against diffusion. (Since it is unlikely that larvae could swim exactly to patch center, this estimate only forms a minimum requirement.) Given that larvae swim one to two body lengths per second, swimming ability can be important in maintaining a patch once the larvae reach a length of 10-20 mm. This mechanism most likely explains the observed increase in P for older larvae (Fig. 3).
Figure 6. The relationship between larval swimming speed and the radius of a patch they are capable of maintaining in the presence of horizontal diffusion. See text for details of the model. Dashed line represents the approximate radius of eddies in Shelikof Strait and the resulting minimum radial swimming speed to maintain the larval patch against diffusion.
Return to previous section or go to next section
