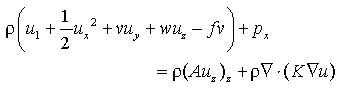 (1)
(1)
U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
In this section we examine the dynamics of month-to-month variations described above through a diagnosis of the zonal momentum equation.
We can write the zonal momentum equation as
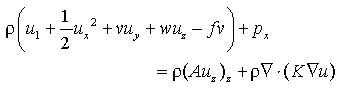 (1)
(1)
where u, v and w are zonal, meridional and vertical velocity
components, p is pressure,  (= 10
(= 10 kg m
kg m ) is density, f is the Coriolis
parameter, A is vertical eddy viscosity and K is horizontal eddy
viscosity. Subscripts denote differentiation and the operator
) is density, f is the Coriolis
parameter, A is vertical eddy viscosity and K is horizontal eddy
viscosity. Subscripts denote differentiation and the operator 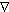 is a horizontal gradient operator. We can neglect the Coriolis term on the equator
since f = 0 there. Horizontal diffusion will also be neglected because
even though it may be important (e.g., Hansen and Paul 1984; Bryden et al. 1986),
it cannot be estimated from only equatorial data.
is a horizontal gradient operator. We can neglect the Coriolis term on the equator
since f = 0 there. Horizontal diffusion will also be neglected because
even though it may be important (e.g., Hansen and Paul 1984; Bryden et al. 1986),
it cannot be estimated from only equatorial data.
Theory indicates that meridional advection of momentum is likely to be important
in the dynamics of the Undercurrent (see section 2 and Philander
and Pacanowski 1980). We would expect therefore that the term vu will be significantly nonzero in the latitudinally sheared zone of the EUC north
and south of the equator. This term can also be large near the surface where
meridional winds can produce significant cross-equatorial flows (e.g., Cane
1979). However, at the depth of the EUC on the equator, vu
will be significantly nonzero in the latitudinally sheared zone of the EUC north
and south of the equator. This term can also be large near the surface where
meridional winds can produce significant cross-equatorial flows (e.g., Cane
1979). However, at the depth of the EUC on the equator, vu will be locally small relative to the pressure gradient since on seasonal time
scales meridional velocity variations are typically only O(1 cm s
will be locally small relative to the pressure gradient since on seasonal time
scales meridional velocity variations are typically only O(1 cm s )
(e.g., Fig. 3) and u
)
(e.g., Fig. 3) and u
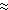 0 by symmetry (Lukas
and Firing 1984). Hence, we neglect vu
0 by symmetry (Lukas
and Firing 1984). Hence, we neglect vu in (1).
in (1).
The vertical diffusion term is not easily estimated from our data because 1) the eddy viscosity is highly variable with depth and precisely known (e.g., Peters et al. 1988) and 2) second derivatives of u would be very noisy computed from data at only seven depths. However, integrating from 0 m to 250 m, we get
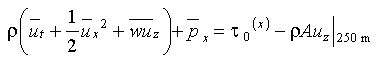 (2)
(2)
where the overbar denotes depth integral, e.g.,
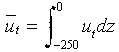
and 

 is the zonal wind stress. For consistency with pressure and stress integrals,
10 m velocity data are first linearly extrapolated to the surface. Differences
between velocity integrals to 0 m and to 10 m are only a few percent, however,
so our results are insensitive to the choice of upper bound. Equation (2), which
governs zonal transport variability, now requires an estimate of A at
only one depth (250 m) and an estimate of zonal velocity shear instead of curvature.
is the zonal wind stress. For consistency with pressure and stress integrals,
10 m velocity data are first linearly extrapolated to the surface. Differences
between velocity integrals to 0 m and to 10 m are only a few percent, however,
so our results are insensitive to the choice of upper bound. Equation (2), which
governs zonal transport variability, now requires an estimate of A at
only one depth (250 m) and an estimate of zonal velocity shear instead of curvature.
We have data from discrete times and depths at the mooring locations from which to calculate terms in (2). We therefore use finite differences in time to estimate acceleration and in depth to estimate vertical shear. We also use finite differences in the zonal direction to estimate the zonal pressure gradient and the zonal advection. To compare two-point zonal gradient estimates of velocity and pressure with other terms in (2), we average zonally to get
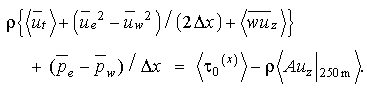 (3)
(3)
The angle brackets denote zonal average, e.g.,
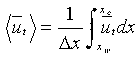
where x and x
and x are eastern and western longitudes and
are eastern and western longitudes and  x
= x
x
= x - x
- x .
For convenience, we will designate the three intervals of 110°-124.5°W, 124.5°-140°W
and 110°-140°W as 117°, 132° and 125°W, respectively.
.
For convenience, we will designate the three intervals of 110°-124.5°W, 124.5°-140°W
and 110°-140°W as 117°, 132° and 125°W, respectively.
Averaging zonal velocity across 15° and 30° of longitude is reasonable given
the high correlations noted for between 110° and 140°W in the previous section.
However, there is an error involved in estimating averages in (3) across an
interval (x , x
, x )
using data from just the end points (Bryden
1977). As an extreme example of how this can affect our results, consider
the 60-90 day wave for which one quarter wavelength fits between 110°and 140°W.
Using Bryden's formulae for a pure progressive sine wave, averages in the angle
brackets would be too low by about 20% relative to the true average. For less
extreme variations across the array, as for example 1/10 to 1/20 of a cycle
in transport at 1 cpy, estimates of average amplitude would be reduced by 10%
or less. Average gradients, i.e. (
)
using data from just the end points (Bryden
1977). As an extreme example of how this can affect our results, consider
the 60-90 day wave for which one quarter wavelength fits between 110°and 140°W.
Using Bryden's formulae for a pure progressive sine wave, averages in the angle
brackets would be too low by about 20% relative to the true average. For less
extreme variations across the array, as for example 1/10 to 1/20 of a cycle
in transport at 1 cpy, estimates of average amplitude would be reduced by 10%
or less. Average gradients, i.e. (

 -
- 

 )/(2
)/(2 x), are exact.
x), are exact.
Zonally averaging zonal wind stress for use in (3) poses a problem because of the large data gaps in the records at each longitude. However, one can see from the solid curves in Fig. 5 that there is a high correlation between records at adjacent mooring sites. Between 110° and 124°W this correlation is 0.96 for 14 monthly mean pairs; and between 124° and 140°W it is 0.94 for 8 monthly mean pairs. Hence, we can use regression analysis based on adjacent locations to fill record gaps for improved zonal averages. These regression fills are shown in Fig. 5 by the dashed lines. Fills were made only for "nearest neighbor" sites since the very tight regression weakens over 30 degrees of longitude to 0.63 between 100° and 140°W.
The nonlinear term ½ u
u
 has been calculated by first forming products of daily data, then smoothing
with the 51-day Hanning filter. Vertical velocity is too weak to measure directly
and we have no reliable way of estimating it from our data. We attempt calculation
of time mean vertical advection in (3) though, using an estimate of w
from Bryden
and Brady's (1985) diagnostic model of the steady equatorial circulation
in the region 110° to 150°W. This mean velocity (their Fig.
7) has a maximum upwelling of about 3 × 10
has been calculated by first forming products of daily data, then smoothing
with the 51-day Hanning filter. Vertical velocity is too weak to measure directly
and we have no reliable way of estimating it from our data. We attempt calculation
of time mean vertical advection in (3) though, using an estimate of w
from Bryden
and Brady's (1985) diagnostic model of the steady equatorial circulation
in the region 110° to 150°W. This mean velocity (their Fig.
7) has a maximum upwelling of about 3 × 10 cm s
cm s at 60 m, crosses zero at about 180
m and shows downwelling at a rate of 1 × 10
at 60 m, crosses zero at about 180
m and shows downwelling at a rate of 1 × 10 cm s
cm s at 250 m. Vertical velocity profiles
similar in magnitude and structure have been estimated from mooring data in
the equatorial Pacific at 110°W (Halpern
and Freitag 1987) and between 110°-150°W (Bryden
et al. 1986).
at 250 m. Vertical velocity profiles
similar in magnitude and structure have been estimated from mooring data in
the equatorial Pacific at 110°W (Halpern
and Freitag 1987) and between 110°-150°W (Bryden
et al. 1986).
Figure 11 shows examples of pressure gradient, local acceleration, and zonal advection before integration over depth for the interval centered at 125°W. Also shown in Fig. 11c is our estimated profile of time mean vertical advection. It is interesting to note that the mean profiles in Figs. 11a and 11c are quantitatively and qualitatively similar to profiles from Bryden and Brady's (1985) diagnostic model of the mean circulation between 110° and 150°W. Their results were based solely on hydrographic data in contrast to ours which are based principally on time series measurements.
Figure 11. Time series estimates of (a) zonal pressure gradient, p ,
relative to 250 m, (b) local acceleration,
,
relative to 250 m, (b) local acceleration,  u
u ,
and (c) zonal advection, ½
,
and (c) zonal advection, ½ u
u
 for the interval centered at 125°W. Contour interval is 1.0 × 10
for the interval centered at 125°W. Contour interval is 1.0 × 10 N m
N m , though the ±0.5 × 10
, though the ±0.5 × 10 N m
N m contour is also drawn. Means are estimated
from a 6-parameter regression fit. Dashed line in the mean panel of (c) is the
vertical advection term
contour is also drawn. Means are estimated
from a 6-parameter regression fit. Dashed line in the mean panel of (c) is the
vertical advection term  WU
WU .
.
Zonal pressure gradient fluctuations (Fig. 11a)
are vertically coherent with largest amplitudes of O(10 N m
N m ) in the upper 100 m, decreasing to zero
at the 250 m reference level. The gradient is always negative with seasonal
minima in boreal spring of each year. However, 60-90 day waves tend to obscure
seasonal variations, especially in the latter part of 1984. A distinct interannual
increase in the gradient is seen between 1983-84 and 1985-86.
) in the upper 100 m, decreasing to zero
at the 250 m reference level. The gradient is always negative with seasonal
minima in boreal spring of each year. However, 60-90 day waves tend to obscure
seasonal variations, especially in the latter part of 1984. A distinct interannual
increase in the gradient is seen between 1983-84 and 1985-86.
Fluctuations in local acceleration of O(10 N m
N m ) (Fig. 11b)
are comparable to those of the pressure gradient. The 60-90 day periodicity
is dominant and tends to be vertically coherent as for the pressure gradient.
There is no obvious evidence of a seasonal variation in
) (Fig. 11b)
are comparable to those of the pressure gradient. The 60-90 day periodicity
is dominant and tends to be vertically coherent as for the pressure gradient.
There is no obvious evidence of a seasonal variation in  U
U ;
nor are there trends in velocity over the record length as indicated by the
near zero mean of acceleration.
;
nor are there trends in velocity over the record length as indicated by the
near zero mean of acceleration.
Zonal advection changes sign at the approximate depth of the EUC core and is
comparable to or larger than the pressure gradient below about 100 m (Fig.
11c). It exhibits an annual cycle between 50-100 m which reflects vertical
movement of the EUC core across these depths (Fig.
6). Also evident is variability at 60-90 day periods of O(10 N m
N m ) in the upper 250 m, as for zonal pressure
gradient and local acceleration.
) in the upper 250 m, as for zonal pressure
gradient and local acceleration.
Mean zonal and vertical advection tend to oppose one another above and below the EUC core (Fig. 11c), consistent with the fact that the EUC shoals towards the east. The tendency for the two terms to cancel suggests that nonlinearity on the zonal plane is important in redistributing momentum in the upper 250 m. However, the cancellation is not complete since near the surface there is a large mean upward advection of eastward momentum from the depth of the EUC core. This leads to a reduction of westward flow at the surface and a large zonal transport along the equator relative to that expected from linear theory (q.v., Philander and Pacanowski 1980).
Figure 12 shows estimates of the terms in the depth integrated momentum balance (3) for the intervals centered at 117°, 125° and 132°W. For convenience we write (3) in a simplified notation given by
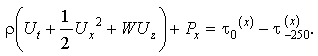 (3')
(3')
Record gaps in the wind stress time series indicate when zonally averaged stress could not be calculated with at least 50% observed data based on the solid curves in Fig. 5. Thus for example, we did not estimate averaged stress in late 1984 and early 1985 across the intervals centered at 117° or 125°W. Overplotted smooth lines are reconstituted time series based on the mean, trend, and 1 cpy harmonics from the regression analyses (Tables 2, 3). The 2 cpy was not included because, except for the zonal winds, this harmonic was generally insignificant.
Figure 12. Estimates (in N m ) of terms
in (3) for the intervals centered at (a) 117°, (b) 125° and (c) 132°W. Shown
in the uppermost panel at each location is ten times the vertical shear stress
at 250 m. Also shown as dotted and long dashed lines are time series reconstituted
from the least squares determined trend, mean, and 1 cpy variations.
) of terms
in (3) for the intervals centered at (a) 117°, (b) 125° and (c) 132°W. Shown
in the uppermost panel at each location is ten times the vertical shear stress
at 250 m. Also shown as dotted and long dashed lines are time series reconstituted
from the least squares determined trend, mean, and 1 cpy variations.
| Longitude | ||||||
|---|---|---|---|---|---|---|
| (°W) | Dates |    |
P |
 U U |
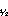  U
U  |
 WU WU |
| 117 | Nov 83–Nov 84 | –24.1 ± 1.8 | –21.9 ± 3.9 | X | X | X |
| 117 | May 84–Sep 85 | X | –27.2 ± 3.4 | (–0.3 ± 7.0) | –5.7 ± 0.9 | –13.2 |
| 125 | Nov 83–Nov 84 | –29.5 ± 2.1 | –28.7 ± 3.1 | (–2.3 ± 6.7) | –7.8 ± 2.6 | –16.1 |
| 125 | June 85–May 86 | –55.5 ± 3.6 | –49.1 ± 4.3 | (0.7 ± 9.8) | –4.9 ± 2.0 | –17.8 |
| 132 | Nov 83–Nov 84 | –34.4 ± 2.5 | –34.3 ± 3.9 | X | X | X |
| 132 | May 84–Sep 85 | –64.3 ± 2.1 | –52.8 ± 4.8 | (0.5 ± 6.5) | –3.2 ± 1.1 | –22.5 |
| Longitude | Dates |    |
P |
 U U |
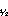  U
U  |
|---|---|---|---|---|---|
| 117 | Nov 83–Nov 84 | ||||
| Amplitude | 12.0 ± 3.5 | 14.0 ± 9.9 | X | X | |
| Phase | 113 ± 29 | 97 ± 47 | X | X | |
| 117 | May 84–Sep 85 | ||||
| Amplitude | X | 8.8 ± 5.1 | (7.8 ± 9.7) | (1.1 ± 1.4) | |
| Phase | X | 99 ± 31 | (41 ± 80) | (251 ± 72) | |
| 125 | Nov 83–Nov 84 | ||||
| Amplitude | 13.7 ± 3.8 | 13.2 ± 8.6 | (6.9 ± 23.7) | (2.6 ± 5.9) | |
| Phase | 115 ± 29 | 89 ± 36 | (45 ± 85) | (289 ± 178) | |
| 125 | June 85–May 86 | ||||
| Amplitude | 19.9 ± 9.7 | 11.6 ± 11.2 | (13.9 ± 37.5) | (3.2 ± 6.5) | |
| Phase | 98 ± 34 | 100 ± 71 | (50 ± 62) | (262 ± 89) | |
| 132 | Nov 83–Nov 84 | ||||
| Amplitude | 15.1 ± 4.7 | 14.4 ± 11.9 | X | X | |
| Phase | 120 ± 33 | 76 ± 37 | X | X | |
| 132 | May 84–Sep 85 | ||||
| Amplitude | 24.2 ± 3.0 | (5.0 ± 7.2) | (8.5 ± 9.1) | 1.6 ± 1.5 | |
| Phase | 149 ± 7 | (133 ± 79) | (44 ± 67) | 36 ± 60 | |
Shown in the uppermost frame at each location is ten times the averaged zonal
shear stress at 250 m calculated using an eddy viscosity of A = 10 m
m s
s . This
choice of A is based on recent microstructure measurements in the thermocline
of the eastern equatorial Pacific (Peters
et al. 1988). Though subject to considerable uncertainty and derived from
data no deeper than 140 m, this value of A leads to estimates of stress
at 250 m that are 100 times smaller than at the surface. Thus, we will neglect
. This
choice of A is based on recent microstructure measurements in the thermocline
of the eastern equatorial Pacific (Peters
et al. 1988). Though subject to considerable uncertainty and derived from
data no deeper than 140 m, this value of A leads to estimates of stress
at 250 m that are 100 times smaller than at the surface. Thus, we will neglect


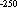 in subsequent discussion since it is unlikely to affect our conclusions.
in subsequent discussion since it is unlikely to affect our conclusions.
To examine the relationship between zonal wind stress and pressure gradient,
we first subsampled the time series every 31 days, then generated scatter diagrams
and linear regression fits for the intervals centered at 117°, 125° and 132°W
(Fig. 13). The correlation between stress and
gradient is positive in all three intervals and is >0.80 at 132° and 125°W.
The slope of the regression lines in these latter two intervals indicates that
on a month-to-month basis, 

 is 10%-20% larger than P
is 10%-20% larger than P .
The inequality could be due to a combination of the shallow 250 m reference
level for P
.
The inequality could be due to a combination of the shallow 250 m reference
level for P , uncertainty
in the wind stress drag coefficient, and the importance of nonlinearity. The
lower correlation between P
, uncertainty
in the wind stress drag coefficient, and the importance of nonlinearity. The
lower correlation between P and
and 

 in the interval centered at 117°W vis-a-vis 132°W may reflect the fact that
the zonal wind stress weakens towards the east (e.g., Fig.
5) so that remote effects take on a larger significance there.
in the interval centered at 117°W vis-a-vis 132°W may reflect the fact that
the zonal wind stress weakens towards the east (e.g., Fig.
5) so that remote effects take on a larger significance there.
Figure 13. Regression analysis of P and
and 

 at (a) 117°W from November 1983 to August 1985; (b) 125°W from November 1983
to April 1986; and (c) 132°W from November 1983 to September 1985. Correlation
coefficients (r) and number of monthly data (n) are shown.
at (a) 117°W from November 1983 to August 1985; (b) 125°W from November 1983
to April 1986; and (c) 132°W from November 1983 to September 1985. Correlation
coefficients (r) and number of monthly data (n) are shown.
Harmonic analyses for simultaneous records centered at 117°, 125° and 132°W are summarized in Tables 2 and 3. Two separate analyses were done at 125°W for approximately year long records bracketing the wind data gap in 1984-85. Similarly, two analyses were done for the intervals centered at 117°W and 132°W, one for November 1983 to November 1984, and one for May 1984 to September 1985.
In the mean, 


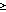 P
P with a maximum difference of 20%; in general, though, these two terms are not
different from one another to within one standard error (Table
2). Both the mean wind stress and the pressure gradient are significantly
stronger in the interval centered at 132°W as compared to 117°W (consistent
with Fig. 1). The nonlinear terms are smaller
than either P
with a maximum difference of 20%; in general, though, these two terms are not
different from one another to within one standard error (Table
2). Both the mean wind stress and the pressure gradient are significantly
stronger in the interval centered at 132°W as compared to 117°W (consistent
with Fig. 1). The nonlinear terms are smaller
than either P or
or 

 with zonal (vertical) advection being
10%-30% (35%-60%) of the pressure gradient. The sign of the nonlinear terms
is always negative implying acceleration of flow to the east, which is consistent
with the observation that the mean eastward transports along the equator are
larger than expected from linear theory. Together ½
with zonal (vertical) advection being
10%-30% (35%-60%) of the pressure gradient. The sign of the nonlinear terms
is always negative implying acceleration of flow to the east, which is consistent
with the observation that the mean eastward transports along the equator are
larger than expected from linear theory. Together ½ U
U
 and
and  WU
WU tend to overcompensate for the difference between wind stress and pressure gradient
by about -10 × 10
tend to overcompensate for the difference between wind stress and pressure gradient
by about -10 × 10 to -20 × 10
to -20 × 10 N m
N m . This imbalance could be due to the
cumulative error involved in estimating terms in (3). However, it could also
be due to the neglect of lateral turbulent diffusion due to instability waves
which lead to an effective zonal stress of about O(-10 × 10
. This imbalance could be due to the
cumulative error involved in estimating terms in (3). However, it could also
be due to the neglect of lateral turbulent diffusion due to instability waves
which lead to an effective zonal stress of about O(-10 × 10 N m
N m ) in the upper 200-300 m of the eastern
tropical Pacific (Hansen
and Paul 1984; Bryden
et al. 1986).
) in the upper 200-300 m of the eastern
tropical Pacific (Hansen
and Paul 1984; Bryden
et al. 1986).
Table 2 also indicates an interannual change in both the zonal wind stress and pressure gradient which nearly double between 110° and 140°W from 1983-84 to 1985-86. Thus the increase in thermocline depth and dynamic height over the record length (Figs. 8b, 10b) can be dynamically related to the increasing strength of the trades. The warmer SSTs in the latter half of the temperature record in the eastern Pacific (q.v., Fig. 8) may be related to the large scale pressure field adjustment to increased winds, since increasing the slope of the thermocline would remove the cold water reservoir further from the surface. This could reduce the efficiency of upwelling, leading to a rise in SST in spite of an expected cooling tendency due to stronger meridional Ekman divergence and zonal advection.
Table 3 presents
data on the annual harmonic in each of the three intervals centered at 117°,
125° and 132°W. We note that zonal wind stress and pressure gradient are generally
comparable in magnitude and phase if one takes into account the uncertainty
of our estimates due to sampling errors. Strongest (weakest) easterlies and
zonal pressure gradients occur from September to November (March to May) depending
on location and specific time period. However, the zonal pressure gradient in
the interval centered at 132°W does not exceed one standard error for the period
May 1984 to September 1985. At this time and location, the 60-90 day waves are
most strongly developed in pressure gradient and are of sufficient amplitude
to obscure the annual cycle. In contrast, there is an approximate balance between
P and
and 

 over the first year of data at 132°W when the waves are weaker.
over the first year of data at 132°W when the waves are weaker.
The local acceleration term,  U
U ,
may be comparable at times to the zonal pressure gradient at 1 cpy, e.g., from
June 1985 to May 1986 in the interval centered at 125°W. However, estimates
of local acceleration are highly uncertain and, unlike zonal pressure gradient,
never exceed one standard error. Also, the zonal advection term does not appear
to be significant at 1 cpy. These results suggest an equilibrium balance between
zonal wind stress and pressure gradient at the annual period.
,
may be comparable at times to the zonal pressure gradient at 1 cpy, e.g., from
June 1985 to May 1986 in the interval centered at 125°W. However, estimates
of local acceleration are highly uncertain and, unlike zonal pressure gradient,
never exceed one standard error. Also, the zonal advection term does not appear
to be significant at 1 cpy. These results suggest an equilibrium balance between
zonal wind stress and pressure gradient at the annual period.
Harmonic analysis indicates that variations at 2 cpy are generally smaller than at 1 cpy and with few exceptions (notably in wind stress) statistically insignificant. Thus, while it is likely that wind-driven 2 cpy variations occur in the eastern equatorial Pacific based on previous historical data analyses and modeling studies (e.g., Meyers 1979; Kindle 1979; Busalacchi and O'Brien 1980), we cannot critically examine the dynamics at this frequency with our data. Conversely, the residuals about our six-parameter regression equation show a consistent pattern. This is illustrated for the interval centered at 132°W during May 1984-September 1985 when 60-90 day wave variability was especially pronounced (Fig. 14); similar results apply to the intervals centered at 125° and 117°W.
Figure 14. Residuals about the mean, trend, 1 and 2 cpy regression for terms
in the dynamical balance (3) at 132°W. Numbers adjacent to the time series are
root-mean-square variations in N m ; maximum
cross correlation with
; maximum
cross correlation with  U
U is shown in parentheses. Maxima generally occur at nonzero lag, with
is shown in parentheses. Maxima generally occur at nonzero lag, with  U
U leading P
leading P ,
, 

 , and ½U
, and ½U
 by 12, -3, an -1 days, respectively.
by 12, -3, an -1 days, respectively.
Figure 14 shows that residuals around the six-parameter
regression fit are dominated by the 60-90 day period, with the largest amplitude
fluctuations in P and
and  U
U .
The maximum correlation between residuals of P
.
The maximum correlation between residuals of P and
and  U
U is -0.66, which is significant at the 95% level of confidence. Residual
is -0.66, which is significant at the 95% level of confidence. Residual  U
U leads P
leads P by 12 days, which
could be due to a phase shift introduced by averaging U
by 12 days, which
could be due to a phase shift introduced by averaging U across longitude in (3). The zonal pressure gradient is weaker than the local
acceleration as would be expected if the residual variability were due to low
baroclinic model Kelvin waves, since the 250 m reference level is too shallow
to capture deep modal pressure variations. Indeed, referencing
across longitude in (3). The zonal pressure gradient is weaker than the local
acceleration as would be expected if the residual variability were due to low
baroclinic model Kelvin waves, since the 250 m reference level is too shallow
to capture deep modal pressure variations. Indeed, referencing  U
U to 250 m brings the magnitude of these two terms into closer agreement. Zonal
wind stress variations are typically weaker than variations in either P
to 250 m brings the magnitude of these two terms into closer agreement. Zonal
wind stress variations are typically weaker than variations in either P or
or  U
U ,
and maximum correlation between residual
,
and maximum correlation between residual 

 and
and  U
U is only 0.42 (not significant
at the 95% level). Thus, it appears that the residual variance is remotely forced
rather than locally forced. The amplitude of the nonlinear term is only about
15% the amplitude of the local acceleration term, but significantly negatively
correlated (-0.66) with
is only 0.42 (not significant
at the 95% level). Thus, it appears that the residual variance is remotely forced
rather than locally forced. The amplitude of the nonlinear term is only about
15% the amplitude of the local acceleration term, but significantly negatively
correlated (-0.66) with  U
U .
Hence, nonlinearity is significant, though of secondary importance on this time
scale.
.
Hence, nonlinearity is significant, though of secondary importance on this time
scale.
Go back to previous section or forward to next section