U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
The data used in this study were collected from taut-wire surface moorings anchored in water 3.7-4.9 km deep (Halpern 1987a). Mooring deployments and recoveries were made approximately every six months for two and a half years (November 1983 to June 1986) on the equator at 108°, 110°, 124.5° and 140°W as part of the TROPIC HEAT and EPOCS programs. Fifteen-minute average currents and temperatures were internally recorded in EG&G; Model 610 Vector Averaging Current Meters (VACM) located at seven depths (10, 25, 45, 80, 120, 160, 250 m) in the upper 250 m at 110°, 124.5° and 140°W. Also, at selected depths between 35 and 200 m, shorter records of temperature sampled every 15 minutes were available. The 108°W mooring was instrumented with three VACMs (at 25, 45 and 80 m) as a backup to the 110°W mooring. Fifteen-minute average vector wind components were also recorded at 110°, 124.5° and 140°W from an inverted VACM equipped with a Climet cup anemometer and vane mounted on the buoy tower 4 m above mean water line. Sea surface temperature (SST) was measured from a thermistor attached to the buoy bridle 1 m below the surface.
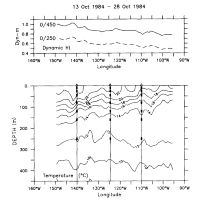
Start and end dates of time series used in this study, number of days of data, and ocean depths are summarized in Table 1 for the moorings at 110°, 124.5° and 140°W. Figure 2 shows the mooring array in relation to the thermal structure and dynamic height field along the equator. The moorings span a range of longitudes where the thermocline slopes downward, dynamic height slopes upward, and SST increases from east to west.
Figure 2. Zonal section of temperature and dynamic height (0/250 m dashed and 0/450 m solid) from XBT casts in October 1985 showing mooring positions and VACM depths.
| Longitude | Duration | Ocean depth | ||
|---|---|---|---|---|
| (°W) | Start date | End date | (days) | (m) |
| 100 | 02 Nov 1983 | 30 May 1986 | 941 | 3750 |
| 124.5 | 29 Oct 1983 | 04 Oct 1985 | 707 | 4870 |
| 140 | 20 Oct 1983 | 13 June 1986 | 968 | 4300 |
Overall data return for currents was 97%. The 80 m current record at 110°W
was replaced by the record at 108°W from October 1984-April 1985 due to a failure
of the recorder at 110°W. Coherence is greater than 0.6-0.7 (significant at
the 95% level of confidence) between these two longitudes at periods longer
than 6-7 days (Halpern
1987a), so it is appropriate to make the substitution when examining month-to-month
variability. Data return for subsurface VACM temperatures at each depth was
generally equal to or higher than that for currents. The data return for SST
and winds was lower, being 70% and 79%, respectively. Instrumental errors for
currents, wind, and temperature are O(1 cm s ),
O(0.1 m s
),
O(0.1 m s ), and O(0.01°C) (Halpern
1987b, 1987c;
Freitag
et al. 1987) and are not expected to adversely affect our results.
), and O(0.01°C) (Halpern
1987b, 1987c;
Freitag
et al. 1987) and are not expected to adversely affect our results.
The 15-minute data were block averaged to daily values, examples of which are shown in Fig. 3 for velocity and temperature at selected depths from the 140°W mooring. (Examples of daily time series from 110°W can be found in Halpern 1987a). Also shown are low-pass versions of the time series smoothed with a 51-day Hanning filter (Bendat and Pierson 1971) which effectively eliminates energy at periods shorter than 25 days. The half-amplitude frequency of this filter is 51 days, so that lower frequencies, which are of primary interest in this study, are relatively unattenuated.
Figure 3. Daily averages of (a) zonal velocity (b) meridional velocity, and (c) temperature at 0°N, 140°W at depths of 25 m, 80 m and 160 m. Smooth curves are for daily data smoothed with a 51-day Hanning filter.
Variance preserving spectra of zonal velocity and temperature at 25 m and 80 m (Fig. 4) show increasing energy at periods longer than about 100 days associated with the seasonal cycle. Temperature shows peaks between 60-90 days at all three depths (25, 80 and 160 m) and zonal velocity shows a similar peak at 160 m. There is as much or more zonal velocity variance at periods of 60-90 days in the 25 and 80 m spectra, though it does not appear in the form of a sharp spectral peak as at 160 m. Meridional velocity is dominated by periods shorter than 60 days, e.g., 20-30 day fluctuations associated with instabilities of the large scale zonal currents (e.g., Philander et al. 1985; Halpern 1987a). Unlike zonal velocity and temperature, there are no significant seasonal or 60-90 day oscillations in this variable.
Figure 4. Variance preserving spectra for zonal velocity and temperature shown in Fig. 3 at 0°N, 140°W for daily data. Spectral estimates are based on averages over five adjacent frequency bands. Note that the ordinates are scaled differently at each depth.
Time averaging eliminates high frequency variations that would otherwise be aliased in monthly estimates of zonal velocity and temperature. It will also reduce spatial aliasing in an array of widely spaced moorings to the extent that short period fluctuations are associated with short spatial scales. For example, zonal variability on scales shorter than the mooring separations is evident in Fig. 2. A portion of that variability is associated with 1000 km long instability waves with periods of 20-30 days. Averaging over the period of these waves will simultaneously reduce the energy in the associated wavenumber band.
Results derived from linear least squares analysis of the smoothed data are quoted throughout the text. Data are fit to a six-parameter regression model similar to that presented in McPhaden (1982) for the mean, linear trend, and 1 and 2 cpy harmonics. Error variances are estimated from the residuals about the regression and assume N-M degrees of freedom where M = 6 is the number of regression model parameters and N is the number of months of data. This choice of N is based on the integral time scale (Davis 1976) which is typically about 30 days for residuals. Confidence limits are derived from standard formulae for means, trends, harmonic, sine and cosine functions (Draper and Smith 1966). Confidence limits for harmonic amplitude and phase are based on formulae presented in Jenkins and Watts (1968). As discussed below, errors in stress (due to uncertain drag coefficient), in pressure gradient (due to reference level of 250 m and use of a mean T- S), and in zonal averages of terms in Eq. (3) may be comparable to sampling errors derived from the regression analysis.
Go back to previous section or forward to next section