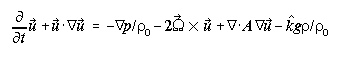 |
(1) |
The model describes a thermal plume rising into a temperature- and salinity-stratified background environment marked by steady, vertically sheared cross flow. The fluid is incompressible and the response to the localized buoyancy source nonhydrostatic. Together with the equation of state for seawater [Fofonoff and Millard, 1983], the underlying model equations in the Boussinesq approximation are
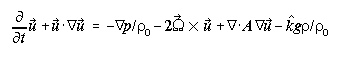 |
(1) |
| (2) |
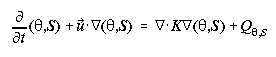 |
(3) |
| (4) |
| (5) |
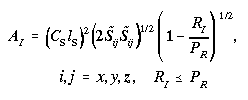 |
(6) |
| (7) |
| (8) |
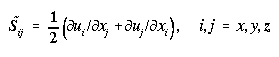 |
(9) |
| (10) |
where t is time; ![]() consists of u, v, and vertical w (positive upward) components;
p is pressure;
consists of u, v, and vertical w (positive upward) components;
p is pressure;  is density;
is density; 
 (1028.11 kg m
(1028.11 kg m ) is a reference density; g
(9.81 m
) is a reference density; g
(9.81 m s
s )
is acceleration of gravity;
)
is acceleration of gravity;  is the rotation
vector; and
is the rotation
vector; and ![]() is the unit vector in the vertical direction. Potential temperature,
is the unit vector in the vertical direction. Potential temperature,  ,
and salinity, S, depend on rates of discharge of heat QH,
via Q
,
and salinity, S, depend on rates of discharge of heat QH,
via Q = QH
/(
= QH
/(
 CP),
and salt QS, where CP (4200 J kg
CP),
and salt QS, where CP (4200 J kg °C
°C ) is the specific heat of seawater. Equations
(1)-(3) are statements of conservation for momentum, mass (given fluid incompressibility),
and heat (or salt). Chemical tracers have conservation equations analogous to
(3). Retention of all terms in the vertical force balance in (1) makes the model
nonhydrostatic. The viscosity tensor A and diffusivity tensor K
are time- and space-dependent; diffusive transport is down gradient.
) is the specific heat of seawater. Equations
(1)-(3) are statements of conservation for momentum, mass (given fluid incompressibility),
and heat (or salt). Chemical tracers have conservation equations analogous to
(3). Retention of all terms in the vertical force balance in (1) makes the model
nonhydrostatic. The viscosity tensor A and diffusivity tensor K
are time- and space-dependent; diffusive transport is down gradient.
Equations (4)-(10) constitute the turbulent mixing submodel. Horizontal and
vertical components of mixing tensors AH or V (and
KH or V via (10)) are each composed of two parts: an
isotropic (AI) mixing coefficient and either horizontal (AHMIN)
or vertical (AVMIN) background terms (equations (4)-(5)).
The isotropic mixing coefficient AI (equation (6)) is made
to depend on fluid shear (Sij, here given in Cartesian form,
(9)), on shear Richardson number (RI (8)), on Prandtl number
(PR (10)), and on the turbulence length scale (lS)
and Smagorinsky (CS) constants (equation (6)). If RI
were zero, (6) would reduce to a form originating with Smagorinsky
[1963]; it stems from an assumed local balance between shear production
and turbulence dissipation in the turbulence kinetic energy (TKE) equation.
When buoyancy production or dissipation is added to the local TKE balance, the
RI dependent factor becomes part of the formulation [Lilly,
1962]. Advection and diffusion of TKE are generally found to represent small
contributions to the TKE equation balance when explicitly evaluated, and they
are here implicitly set to zero. Mixing terms have no explicit dependence on
rotation. The reason is that in forming TKE, terms involving  sum to zero.
sum to zero.
Smagorinsky-Lilly mixing, with or without the RI dependent factor, is in widespread use in atmospheric calculations [e.g., Clark and Farley, 1984; Mason, 1989]. Subgrid-scale mixing of this type is frequently used in large eddy simulations (LES) of both engineering and geophysical natures [e.g., Reynolds, 1990; Galperin and Orszag; 1993; Smagorinsky, 1993; Mason, 1994]. Following the nomenclature of Reynolds [1990], Wyngaard [1990] notes that models using this kind of turbulence closure should actually be typed very large eddy simulation (VLES). VLES implies that, although resolved scales include much of the eddy energy, model resolution is not high enough that smallest resolved scales fall within the subinertial range of turbulence where details of dissipation ought not to matter.
Background mixing terms (equations (4)-(5)), presumed to be small, have here been added to AI to ensure a modest amount of mixing in regions without shear, e.g., away from the plume region, where AI will be zero. Other closure models are in current use as well. Sykes et al. [1986] used a full TKE equation to determine q, the square root of twice TKE; turbulent mixing was then made proportional to the product of q and lS. In both the present, Sykes et al.'s, and many other approaches, lS has a size that is imposed rather than calculated. The model summarized by (1)-(10), but without cross flow, has been studied in the context of laboratory convection experiments as a way of investigating the value of the subgrid turbulence closure subcomponent [Lavelle and Smith, 1996].
For hydrothermal venting, convective flow is forced by a source of heat at
interior points along the lower boundary of the region of interest. Steady background
cross flow is forced by a constant horizontal pressure gradient, 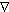 P
P .
Without point source heating, the steady background velocity profile uBKG
= (uBKG, vBKG) results from an Ekman horizontal
force balance (equation (1)):
.
Without point source heating, the steady background velocity profile uBKG
= (uBKG, vBKG) results from an Ekman horizontal
force balance (equation (1)):
- 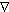 P P / /  - 2
- 2  × uBKG + d/dz
[Az d(uBKG)/dz] =
0 × uBKG + d/dz
[Az d(uBKG)/dz] =
0 |
(11) |
and boundary conditions uBKG = 0 (z = 0, bottom) and
duBKG/dz = 0 (z = h, top). With
uniform 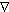 P
P in the y direction, nonzero
in the y direction, nonzero  , and Az
profiles that increase toward the seafloor as described later, flow is oriented
in the x direction except near the bed. Profiles uBKG
and vBKG (e.g., Figure 1a)
were used to initialize velocity fields and maintain upstream velocity boundary
conditions thereafter. Without source heat (and/or salt), uBKG and
vBKG are maintained numerically over time as solutions to
(1)-(10) as they must be. In reference experiment 21 (Table 1), outside the
boundary layer, uBKG was 1.5 cm s
, and Az
profiles that increase toward the seafloor as described later, flow is oriented
in the x direction except near the bed. Profiles uBKG
and vBKG (e.g., Figure 1a)
were used to initialize velocity fields and maintain upstream velocity boundary
conditions thereafter. Without source heat (and/or salt), uBKG and
vBKG are maintained numerically over time as solutions to
(1)-(10) as they must be. In reference experiment 21 (Table 1), outside the
boundary layer, uBKG was 1.5 cm s ,
while vBKG was nonzero only within that layer (Figure
1a). Mean currents of that magnitude are typical at ridge crest depths on
the JDFR [e.g.,
Cannon et al., 1991].
,
while vBKG was nonzero only within that layer (Figure
1a). Mean currents of that magnitude are typical at ridge crest depths on
the JDFR [e.g.,
Cannon et al., 1991].
Figure 1. Idealized environmental profiles for u, v,
AZ,  , S, and
, S, and  .
Profile shapes and magnitudes nominally represent conditions in the lowest 300
m of water column above the seafloor spreading center of the Juan de Fuca Ridge,
northeast Pacific. The AZ profile controlling the boundary
layer thickness is hypothetical, but the shape and magnitude are generally consistent
with AZ values deduced from benthic ocean measurements at
other sites.
.
Profile shapes and magnitudes nominally represent conditions in the lowest 300
m of water column above the seafloor spreading center of the Juan de Fuca Ridge,
northeast Pacific. The AZ profile controlling the boundary
layer thickness is hypothetical, but the shape and magnitude are generally consistent
with AZ values deduced from benthic ocean measurements at
other sites.
Table 1. Parameter Values for the Convective Plume Experiments
| Exp. No. | 2 Z, Z,s  |
CS | AH
MIN, cm  s s |
U , ,m s  |
h,
m |
| 21 | 1.03 × 10 |
0.2 | 100 | 0.015 | 300 |
| 22 | 0 | 0.2 | 100 | 0.015 | 300 |
| 23 | 1.03 × 10 |
0 | 100 | 0.015 | 300 |
| 26 | 1.03 × 10 |
0.2 | 10 | 0.015 | 300 |
| 24 | 1.03 × 10 |
0.2 | 100 | 0.03 | 200 |
| 25 | 1.03 × 10 |
0.2 | 100 | 0.06 | 150 |
The vertical force balance without heating is hydrostatic: dP /dz
= g
/dz
= g BKG, where
BKG, where  BKG
is background density; wBKG = 0. The variable p in (1)
thus represents the sum of P
BKG
is background density; wBKG = 0. The variable p in (1)
thus represents the sum of P (z),
P
(z),
P (x,y), and
a perturbation pressure p
(x,y), and
a perturbation pressure p (x,y,z)
caused by heating. In actual practice, hydrostatic terms are first subtracted
from (1), with the consequence that in resulting equations, p represents
the sum of P
(x,y,z)
caused by heating. In actual practice, hydrostatic terms are first subtracted
from (1), with the consequence that in resulting equations, p represents
the sum of P and p
and p and
and  becomes
becomes 
 = (
= ( -
-  BKG
).
BKG
).
Background profiles (Figures 1a-1b) hinge on
the form given Az. To simplify the initialization process
and make background profiles independent of boundary layer shear,  of (4) was set to zero. Vertical turbulent mixing coefficients are thus fixed
from the start of calculations. Because vertical mixing rates in the ocean are
small in the interior (AZMIN) and increase (to AZMAX)
as z
of (4) was set to zero. Vertical turbulent mixing coefficients are thus fixed
from the start of calculations. Because vertical mixing rates in the ocean are
small in the interior (AZMIN) and increase (to AZMAX)
as z  0 [e.g.,
Garrett, 1979], the profile for A
0 [e.g.,
Garrett, 1979], the profile for A (Figure 1a) was given the form
(Figure 1a) was given the form
| (12) |
where hB determines the boundary layer thickness. The value
of Az declines to within 1% of AZMIN by
a distance of 5 hB of the seafloor (z = 0). Values
of AZMIN = 1 cm s
s ,
AZMAX = 100 cm
,
AZMAX = 100 cm s
s ,
and a viscosity height scale length hB = 10 m were taken as
nominally representative of benthic ocean conditions.
,
and a viscosity height scale length hB = 10 m were taken as
nominally representative of benthic ocean conditions.
Without heating, background profiles  BKG
and SBKG must be time-invariant and laterally uniform. Since
wBKG = 0, (3) in that case leads to
BKG
and SBKG must be time-invariant and laterally uniform. Since
wBKG = 0, (3) in that case leads to
d/dz [K (d
(d BKG/dz)]
= 0 BKG/dz)]
= 0 |
(13) |
or once integrated over depth interval [z,h],
K [d
[d BKG/dz]
= F0 BKG/dz]
= F0 |
(14) |
where F0 is a constant the
value of which is set by conditions at z = h. Over depth interval
[0,h], profiles of Kz and
is a constant the
value of which is set by conditions at z = h. Over depth interval
[0,h], profiles of Kz and  BKG
are thus linked; where K
BKG
are thus linked; where K grows
large near the seafloor, d
grows
large near the seafloor, d BKG/dz
must adjust appropriately. Equations (13)-(14) imply that to maintain a steady
BKG/dz
must adjust appropriately. Equations (13)-(14) imply that to maintain a steady
 BKG profile, the gradient flux of
BKG profile, the gradient flux of
 BKG must be balanced by a vertical
flux of opposite sign. Otherwise, background profiles would continually change,
making more difficult the resolution of small temperature anomalies caused only
by hydrothermal heating. Analogous arguments apply to SBKG.
BKG must be balanced by a vertical
flux of opposite sign. Otherwise, background profiles would continually change,
making more difficult the resolution of small temperature anomalies caused only
by hydrothermal heating. Analogous arguments apply to SBKG.
Above a boundary layer, background profiles of  and S were taken to be linear:
and S were taken to be linear:  =
= 
 (1 +
(1 + 

![]() )
and S = S0 (1 +
)
and S = S0 (1 + 

![]() )
, where
)
, where 
 ,
S
,
S ,
, 
 ,
and
,
and 
 were given the values 1.6339°C, 34.616
were given the values 1.6339°C, 34.616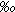 , 1.8925
× 10
, 1.8925
× 10 m
m ,
and -1.5751 × 10
,
and -1.5751 × 10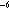 m
m and where
and where ![]() is height above the sea floor. These values are taken from linear least squares
fits of hydrographic profile data from the JDFR over the 2100-2400 m depth range,
profiles judged least affected by hydrothermal influences. Given those profiles
and (14), F0
is height above the sea floor. These values are taken from linear least squares
fits of hydrographic profile data from the JDFR over the 2100-2400 m depth range,
profiles judged least affected by hydrothermal influences. Given those profiles
and (14), F0 =
= 

 0K
0K (z = h) and F0S =
(z = h) and F0S =  2S
2S K
K (z = h). Since A
(z = h). Since A (z
= h) = 10
(z
= h) = 10 m
m s
s (equation (12)) and PR
= 1.0 (equation (10)), F0
(equation (12)) and PR
= 1.0 (equation (10)), F0 = 3.1 × 10
= 3.1 × 10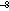 °C m
°C m s
s and F0S = 5.5
× 10
and F0S = 5.5
× 10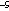
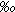 m
m s
s .
.
Integrating (4) with the A profile of (12) for PR = 1.0 results in the background profile
profile of (12) for PR = 1.0 results in the background profile
 BKG for 0 < z < h:
BKG for 0 < z < h:
| (15) |
having a well-mixed boundary layer (Figure 1b),
the height (~50 m) of which is determined by hB. In (15),
 K represents (KZMAX
- KZMIN). A like equation can be written for SBKG.
For z >> hB, the second term of (15) is negligible.
As with velocity,
K represents (KZMAX
- KZMIN). A like equation can be written for SBKG.
For z >> hB, the second term of (15) is negligible.
As with velocity,  BKG and SBKG
profiles (Figure 1b) are used to initialize fields
and provide upstream boundary profiles. Note in Figure
1 that where gradients of
BKG and SBKG
profiles (Figure 1b) are used to initialize fields
and provide upstream boundary profiles. Note in Figure
1 that where gradients of  and S
are large, velocity shear is small, and vice versa. This situation suppresses
shear instabilities that might otherwise develop. It follows that
and S
are large, velocity shear is small, and vice versa. This situation suppresses
shear instabilities that might otherwise develop. It follows that 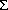 =
=  - 1000 has a similarly well-mixed boundary
layer (Figure 1b). Buoyancy frequency, N,
over depths 2100-2350 m is 7.9 × 10
- 1000 has a similarly well-mixed boundary
layer (Figure 1b). Buoyancy frequency, N,
over depths 2100-2350 m is 7.9 × 10 s
s .
.
A resolved Ekman boundary layer serves these purposes. It allows for directional
shear of flow that can influence plume dispersion. It reduces flow speed in
the boundary layer, flow that can affect entrainment of fluid into the plume
stem, particularly on the downstream side. Finally, a resolved boundary layer
is particularly important for plumes the B of which is not great enough to cause the plumes to rise distinctly above the
seafloor. Diffuse low-temperature sources of hydrothermal heat are instances
of that situation [Trivett
and Williams, 1994].
of which is not great enough to cause the plumes to rise distinctly above the
seafloor. Diffuse low-temperature sources of hydrothermal heat are instances
of that situation [Trivett
and Williams, 1994].
Equations (1)-(10) were integrated over a rectangular domain with boundaries open in x, cyclic in y, and fixed in z. Specifically, conditions were
Lateral inflow boundary, x = X1
| u = uBKG v = vBKG w = 0  =
=  BKG BKG S = SBKG. |
(16) |
Lateral outflow boundary, x = X
uXXX = vXX
= wXX =  X
= SX = 0. X
= SX = 0. |
(17) |
Lower boundary, z = 0
| u = v = w = 0 Kz [   / / z]
= F0 z]
= F0 Kz [  S/ S/ z]
= F0S. z]
= F0S. |
(18) |
Upper boundary, z = h
 u/ u/ z
= z
=  v/ v/ z
= w = 0 z
= w = 0 Kz [   / / z]
= F0 z]
= F0 Kz [  S/ S/ z]
= F0S. z]
= F0S. |
(19) |
Front and back boundaries, y = Y and y = Y
and y = Y
| (20) |
Boundary conditions on p in the x and z directions were
taken in the manner of Harlow
and Welch [1965]. Cyclic conditions were used in the y direction
for all variables (u, v, w,  ,
S, and p) for two reasons: so the Ekman boundary layer of the
background flow would be uniform across the region of calculation and so plumes
could pass though y boundaries as if transparent. Cross-flow strength
and width of the solution domain were always large enough that the downstream
plume never filled the domain side to side, though in some cases the plume passed
through y boundaries. Boundary openness in the x direction was
essential to allow passage of heat and tracers out of the domain, which if prevented
would disallow any thermal equilibrium state from being reached. X direction
boundary conditions are those suggested by Johansson
[1993]. In these experiments, no absorbing layers [e.g.,
Clark and Farley, 1984] were used to damp waves.
,
S, and p) for two reasons: so the Ekman boundary layer of the
background flow would be uniform across the region of calculation and so plumes
could pass though y boundaries as if transparent. Cross-flow strength
and width of the solution domain were always large enough that the downstream
plume never filled the domain side to side, though in some cases the plume passed
through y boundaries. Boundary openness in the x direction was
essential to allow passage of heat and tracers out of the domain, which if prevented
would disallow any thermal equilibrium state from being reached. X direction
boundary conditions are those suggested by Johansson
[1993]. In these experiments, no absorbing layers [e.g.,
Clark and Farley, 1984] were used to damp waves.
As with background profiles, length scales, B ,
and background
,
and background  were chosen with regard to
conditions for chronic hydrothermal plumes at the JDFR. Equations were solved
in a Cartesian domain 640 × 320 × 300 m when U
were chosen with regard to
conditions for chronic hydrothermal plumes at the JDFR. Equations were solved
in a Cartesian domain 640 × 320 × 300 m when U was 1.5 cm s
was 1.5 cm s , but domain height was reduced
to 200 and then 150 m for increasingly larger U0 (Table 1).
Domain depth h was chosen for each U
, but domain height was reduced
to 200 and then 150 m for increasingly larger U0 (Table 1).
Domain depth h was chosen for each U so that plumes penetrated to ~ 0.5 h.
so that plumes penetrated to ~ 0.5 h.  x,
x,
 y,
y,  z,
z,
 t were 5, 5, and 9.4 (6.2 or 4.7) m,
and 15 s, respectively. N
t were 5, 5, and 9.4 (6.2 or 4.7) m,
and 15 s, respectively. N ,
Ny, Nz, and N
,
Ny, Nz, and N were 128, 64, 32, and 2000 (or 5760).
were 128, 64, 32, and 2000 (or 5760).
The source region was 10 × 10 m and was centered at the horizontal location (x,y) = (-105, 0) m; source lateral dimension will hereafter be represented by D. Individual hydrothermal vents have smaller surface cross sections, but separate vents can be clustered in fields [Ginster et al., 1994], or the hydrothermal source may be diffuse, like the sulfide mounds described by Schultz et al. [1992]. The intention here was to model plumes not from a single vent, but from a small composite venting source or vent field. Resolving a single small vent and its regional plume is beyond present computational resources. Model source area was thus chosen to be representative of typical vent field and sulfide mound surface areas. Despite having an extended area, the source is nonetheless point-like in that rise height, hRISE, is very much greater than D.
Source heat flux, Q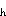 , was
set at 1.3 × 10
, was
set at 1.3 × 10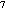 J s
J s (13 MW), a value chosen to cause maximum plume rise of ~200 m under reference
experiment conditions. Since buoyancy flux B
(13 MW), a value chosen to cause maximum plume rise of ~200 m under reference
experiment conditions. Since buoyancy flux B = g
= g Q
Q /
/
 /CP,
where
/CP,
where  is the thermal expansion coefficient
(7.3 × 10
is the thermal expansion coefficient
(7.3 × 10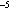 °C
°C ),
B
),
B was fixed at 2.1 × 10
was fixed at 2.1 × 10 m
m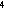 s
s . Buoyancy
flux density was consequently 2.1 × 10
. Buoyancy
flux density was consequently 2.1 × 10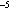 m
m s
s .
.
The value assigned QH is consistent with the wide range of
heat fluxes measured for single vents when extrapolated to a small vent field.
For 18 vents on the southern Juan de Fuca Ridge, Bemis
et al. [1993] estimated an average heat flux of 0.1-3.1 MW per vent.
Ginster
et al. [1994] indicated an average heat output of 3.1 MW for single
high-temperature vents on the southern JDFR and higher values on the ridge's
northerly Endeavor segment, where hydrothermal plumes can reach 300 m above
the seafloor. There their estimated heat flux density of 0.139 MW m would, over a source area of 10 × 10 m, give a Q
would, over a source area of 10 × 10 m, give a Q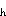 very much like the 13 MW heat flux value used in these calculations. Schultz
et al. [1992] estimated a heat flux of 58 MW from a 4 × 5 m sulfide
mound at Endeavor.
very much like the 13 MW heat flux value used in these calculations. Schultz
et al. [1992] estimated a heat flux of 58 MW from a 4 × 5 m sulfide
mound at Endeavor.
Calculations were made for a site latitude of 45°N. With the nonvertical component
of rotation set to zero, the rotation vector (
 ,
,

 ,
,

 )
was (0, 0, 5.14 × 10
)
was (0, 0, 5.14 × 10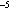 s
s );
an example of the effect of nonzero
);
an example of the effect of nonzero 
 [Garwood
et al., 1985] on a hydrothermal plume is given by Lavelle
[1995]. Mixing parameters were typically AHMIN = 10
[Garwood
et al., 1985] on a hydrothermal plume is given by Lavelle
[1995]. Mixing parameters were typically AHMIN = 10 m
m s
s and
AVMIN = 10-4 m
and
AVMIN = 10-4 m s
s . CS was set to 0.2,
and PR, the ratio of turbulent viscosity to diffusivity, was
given the value 1. Mixing length, ls, was made equal to (
. CS was set to 0.2,
and PR, the ratio of turbulent viscosity to diffusivity, was
given the value 1. Mixing length, ls, was made equal to ( x
x y
y z)1/3
[e.g.,
Reynolds, 1990]. Values for lS, CS,
and PR are not uniquely assignable, but values here are in
ranges commonly used. Sensitivity of results to these parameters can be found,
in part, in studies of axisymmetric plumes by Lavelle
and Baker [1994] and of plumes from line segment sources by Lavelle
[1995].
z)1/3
[e.g.,
Reynolds, 1990]. Values for lS, CS,
and PR are not uniquely assignable, but values here are in
ranges commonly used. Sensitivity of results to these parameters can be found,
in part, in studies of axisymmetric plumes by Lavelle
and Baker [1994] and of plumes from line segment sources by Lavelle
[1995].
Time and length scales pertinent to the development of convective plumes from
point and extended sources in rotating but otherwise quiescent background environments
may be found in the recent work of Jones
and Marshall [1993], Maxworthy
and Narimousa [1994], and Speer
and Marshall [1995]. For point sources and under stratified and depth-unlimited
conditions, the external set of three variables, B ,
f, and N, allows two length scales to be derived. The first, well
known from nonrotating conditions, is lN = (B
,
f, and N, allows two length scales to be derived. The first, well
known from nonrotating conditions, is lN = (B /N
/N )1/4
[e.g.,
Turner, 1973]. By replacing N by f, a second length
scale is uncovered: lf = (B
)1/4
[e.g.,
Turner, 1973]. By replacing N by f, a second length
scale is uncovered: lf = (B /f
3)1/4 [e.g.,
Speer and Marshall, 1995] or lROT = (B
/f
3)1/4 [e.g.,
Speer and Marshall, 1995] or lROT = (B /f
3)½, where B
/f
3)½, where B in the last equation is buoyancy flux density rather than total buoyancy flux
[Maxworthy
and Narimousa, 1994]. Atmospheric and laboratory observations for plumes
rising in nonrotating environments without cross flow have established that
maximum rise height, hRISE, scales like lN:
hRISE ~ 3.75 lN [e.g.,
Hanna et al., 1982]. An example in which lROT was
found to be relevant comes from rotating tank studies of Maxworthy
and Narimousa [1994] on brine convection. They found that once a brine
from a distributed (i.e., nonpoint) source reached a fluid depth of the order
of 12.7 lROT, convection transitioned from a three-dimensional
turbulent condition to one dominated by descending vortical columns. Length
scales such as l
in the last equation is buoyancy flux density rather than total buoyancy flux
[Maxworthy
and Narimousa, 1994]. Atmospheric and laboratory observations for plumes
rising in nonrotating environments without cross flow have established that
maximum rise height, hRISE, scales like lN:
hRISE ~ 3.75 lN [e.g.,
Hanna et al., 1982]. An example in which lROT was
found to be relevant comes from rotating tank studies of Maxworthy
and Narimousa [1994] on brine convection. They found that once a brine
from a distributed (i.e., nonpoint) source reached a fluid depth of the order
of 12.7 lROT, convection transitioned from a three-dimensional
turbulent condition to one dominated by descending vortical columns. Length
scales such as l and lROT
help organize experimental, observational, and occasionally numerical [e.g.,
Speer and Marshall, 1995; Lavelle
and Smith, 1996] results, but in all cases the coefficient of scaling
must be determined from data.
and lROT
help organize experimental, observational, and occasionally numerical [e.g.,
Speer and Marshall, 1995; Lavelle
and Smith, 1996] results, but in all cases the coefficient of scaling
must be determined from data.
Previous modeling work on hydrothermal megaplumes, which are caused by short-lived
thermal releases associated with episodic tectonic events [e.g.,
Embley et al., 1995], have confirmed the utility of those scales
in such cases. Speer
and Marshall [1995] used lf and the timescale for
Coriolis effects to be important, f -1, to scale rotational
velocities in the counterrotating vortices that should develop during megaplume
formation. Lavelle
and Baker [1994] and Speer
and Marshall [1995] found that l scales rise height as it does in the nonrotating case under typical benthic
ocean conditions, and Lavelle
[1995] has shown that the timescale for megaplumes reaching hRISE
is ~ 4N
scales rise height as it does in the nonrotating case under typical benthic
ocean conditions, and Lavelle
[1995] has shown that the timescale for megaplumes reaching hRISE
is ~ 4N . The fact that megaplumes
form quickly permits the modeling assumption of a quiescent background.
. The fact that megaplumes
form quickly permits the modeling assumption of a quiescent background.
In the case of chronically discharging hydrothermal plumes, the assumption
of a quiescent background environment is no longer tenable. Furthermore, these
more typical hydrothermal plumes are not products of ephemeral sources of heat.
They do not produce bottom-detached lenses of water, the geostrophic adjustment
of which Gill
[1981] and McWilliams
[1988] have studied. Consequently, one must not expect that such plumes
are associated with a Burger number ~1 nor expect that the description of bent-over
plumes should involve length scales l and lf, as is made clear below.
and lf, as is made clear below.
In the case of continuous discharging plumes in a cross flow, the set of external
variables from which length scales can be constructed is increased from three
to four: the variable U must
be added to the previous set. Generalized length scales that result from the
expanded set are B
must
be added to the previous set. Generalized length scales that result from the
expanded set are B (1+
(1+ )
N
)
N U
U (-3-4
(-3-4 ) and B
) and B (1+
(1+ )
f
)
f  U
U (-3-4
(-3-4 ).
When
).
When  = -1, advective length scales LNADV
= U
= -1, advective length scales LNADV
= U /N and LfADV
= U
/N and LfADV
= U /f emerge. When
/f emerge. When
 = -3/4, lN and lf
are recovered. But
= -3/4, lN and lf
are recovered. But  can take other values. Atmospheric
and laboratory observations of plume in a cross flow show that lN
(i.e.,
can take other values. Atmospheric
and laboratory observations of plume in a cross flow show that lN
(i.e.,  = -1) is not an appropriate scaling
for plume rise height, for example. Those data (and entrainment theory, e.g.,
Middleton
[1986]) point to a value for
= -1) is not an appropriate scaling
for plume rise height, for example. Those data (and entrainment theory, e.g.,
Middleton
[1986]) point to a value for  that is more
nearly -2/3, so that rise heights of plumes in cross flows scale like lCROSS
= [B
that is more
nearly -2/3, so that rise heights of plumes in cross flows scale like lCROSS
= [B /(U
/(U N
N )]1/3
[e.g,
Hanna et al., 1982], not like [B
)]1/3
[e.g,
Hanna et al., 1982], not like [B N
N ]1/4
as in cases without background flow. For plumes in a cross flow, it is only
through observations that the coefficient of scaling and indeed even the value
of
]1/4
as in cases without background flow. For plumes in a cross flow, it is only
through observations that the coefficient of scaling and indeed even the value
of  can be found. Neither l
can be found. Neither l or lf have demonstrated roles in the scaling of cross-flow
plume results.
or lf have demonstrated roles in the scaling of cross-flow
plume results.
Transverse width of the plume is an important measure of the likelihood of
counterrotating vortex pair development seen in studies of plume formation in
quiescent backgrounds [e.g.,
Speer, 1989]. But it is clear that the width of a plume transverse
to the cross-flow direction cannot scale like LNADV, LfADV,
l or lf,
except in the limit U
or lf,
except in the limit U
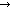 0: plumes having the same source B
0: plumes having the same source B grow narrower with increasing U
grow narrower with increasing U ,
but none of those four scales permit plumes with that U0 dependence.
The width must be inversely proportional to some power of cross-flow velocity,
perhaps scaling as lCROSS. The same arguments can be made
that l
,
but none of those four scales permit plumes with that U0 dependence.
The width must be inversely proportional to some power of cross-flow velocity,
perhaps scaling as lCROSS. The same arguments can be made
that l and lf
play no role in setting plume height. For the cross-flow magnitudes studied
in this paper, plume width above the source is always much less than lf,
the size at which one might expect the Coriolis force to cause counterrotating
vortices in the manner previously predicted for plumes without background flow
[Lavelle
and Baker, 1994; Speer
and Marshall, 1995]. Balancing vertical and horizontal mass flux at
the top of the plume stem in simple calculations leads to that conclusion too.
For the smallest U0 studied in the paper, cross flow overwhelms
upstream density-driven flow in the plume cap above the source. With U
and lf
play no role in setting plume height. For the cross-flow magnitudes studied
in this paper, plume width above the source is always much less than lf,
the size at which one might expect the Coriolis force to cause counterrotating
vortices in the manner previously predicted for plumes without background flow
[Lavelle
and Baker, 1994; Speer
and Marshall, 1995]. Balancing vertical and horizontal mass flux at
the top of the plume stem in simple calculations leads to that conclusion too.
For the smallest U0 studied in the paper, cross flow overwhelms
upstream density-driven flow in the plume cap above the source. With U larger than the density-driven upstream velocity in the plume cap, the plume
bends forward. With U
larger than the density-driven upstream velocity in the plume cap, the plume
bends forward. With U and
B
and
B typical of chronic hydrothermal
discharge conditions, the cross-flow carries plume mass injected to the level
of neutral buoyancy away at a rate that prevents a cross-flow dimension of the
plume to approach lf there.
typical of chronic hydrothermal
discharge conditions, the cross-flow carries plume mass injected to the level
of neutral buoyancy away at a rate that prevents a cross-flow dimension of the
plume to approach lf there.
An interesting transition to the axisymmetric plume case should occur in a
sequence of plumes as U
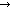 0. Then one can expect the plume to first develop an anvil shape, with some
upstream progression of the plume and some widening of the plume in the transverse
direction. At even smaller U
0. Then one can expect the plume to first develop an anvil shape, with some
upstream progression of the plume and some widening of the plume in the transverse
direction. At even smaller U ,
the plume must begin to take on all the conditions of plumes described in earlier
papers, including a counterrotating vortex pair. U
,
the plume must begin to take on all the conditions of plumes described in earlier
papers, including a counterrotating vortex pair. U ,
of course, drops out of the scaling arguments in this limit and l
,
of course, drops out of the scaling arguments in this limit and l and lf prevail. The study of that transition from cross flow
to axisymmetric plumes has not been undertaken, nor have enough cross-flow experiments
been run that the process of scaling confirmation analogous to those of Speer
and Marshall [1995] or Lavelle
and Smith [1996] is possible now.
and lf prevail. The study of that transition from cross flow
to axisymmetric plumes has not been undertaken, nor have enough cross-flow experiments
been run that the process of scaling confirmation analogous to those of Speer
and Marshall [1995] or Lavelle
and Smith [1996] is possible now.
Momentum equations were centered differenced in space in energy conservation
form and leapfrogged in time. An Asselin [Asselin,
1972] filter having 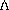 = 0.15 was applied
each time step to control temporal mode splitting. Integrations involved solving
a 3-D Poisson equation for p [Harlow
and Welch, 1965] on a staggered grid each time step using direct method
solvers HS3CRI and HS3CRT (R. Sweet, National Bureau of Standards, Boulder,
Colorado, 1985). Transport equations were forward time differenced. Their diffusion
terms were centered differenced in space, while advection terms were upstream
differenced but corrected each time step for unwanted numerical diffusion using
the procedure of Smolarkiewicz
[1983] and Smolarkiewicz
and Clark [1986]. Even in the presence of strong advection, upstream
differencing with correction can maintain relatively sharp property gradients
like those found at plume stem walls, while maintaining positive definiteness
of calculated quantities. The last attribute proves useful in eliminating the
occurrence of unphysically low property anomalies.
= 0.15 was applied
each time step to control temporal mode splitting. Integrations involved solving
a 3-D Poisson equation for p [Harlow
and Welch, 1965] on a staggered grid each time step using direct method
solvers HS3CRI and HS3CRT (R. Sweet, National Bureau of Standards, Boulder,
Colorado, 1985). Transport equations were forward time differenced. Their diffusion
terms were centered differenced in space, while advection terms were upstream
differenced but corrected each time step for unwanted numerical diffusion using
the procedure of Smolarkiewicz
[1983] and Smolarkiewicz
and Clark [1986]. Even in the presence of strong advection, upstream
differencing with correction can maintain relatively sharp property gradients
like those found at plume stem walls, while maintaining positive definiteness
of calculated quantities. The last attribute proves useful in eliminating the
occurrence of unphysically low property anomalies.
The accuracy of the model has been examined in the following ways. Requisite
conservation of mass, momentum, heat, salt, and energy was carefully checked
under a variety of forcing, as was symmetry (or antisymmetry) of all field variables
under symmetric forcing. Conditions for the independence of results from model
grid size were examined by Lavelle
and Baker [1994] using the axisymmetric realization of the model. Results
on sensitivity to the Smagorinsky coefficient and Prandtl number and on the
model relationship of plume rise height to buoyancy flux B0
are found in the same place. Additional sensitivity experiments, specifically
for rise height dependence on buoyancy flux and buoyancy frequency N,
were conducted for a line segment hydrothermal source rising into a quiescent
background environment [Lavelle,
1995]. That analysis demonstrated that the rise height of the model scales
as B 1/3 in a quiescent
background setting, as would be expected for that source configuration. Model
results on the scaling of plume rise height with cross-flow strength are also
encouraging. Atmospheric observations show plume rise height hRISE
depending on the cross-flow velocity U
1/3 in a quiescent
background setting, as would be expected for that source configuration. Model
results on the scaling of plume rise height with cross-flow strength are also
encouraging. Atmospheric observations show plume rise height hRISE
depending on the cross-flow velocity U as U
as U -
- ,
where
,
where  is ~1/3 [Hanna
et al., 1982]. As demonstrated later, this model shows a rise height
dependence on cross-flow velocity of U
is ~1/3 [Hanna
et al., 1982]. As demonstrated later, this model shows a rise height
dependence on cross-flow velocity of U -0.4,
with a coefficient of proportionality of similar magnitude to atmospheric cases.
-0.4,
with a coefficient of proportionality of similar magnitude to atmospheric cases.
Additional comparisons of model results to laboratory and field observations have been made. The utility of the Smagorinksy-Lilly subgrid-scale turbulence formulation was examined [Lavelle and Smith, 1996] by comparing model with laboratory results [Fernando and Ching, 1993] for a brine convection in a rotating tank. The importance of self-generated turbulence during convection has long been recognized [e.g., Priestly, 1956], and those numerical experiments in conjunction with laboratory results have reconfirmed the view that time- and space-dependent turbulence closure is essential. Furthermore, this model, under conditions of cross flow in a nonrotating environment, produces flow patterns comparable to the numerical results of Sykes et al. [1986] and to experimental results they cite, as will be described more fully below. Finally, hydrographic profiles from this model for regions affected by chronic hydrothermal sources have the form and magnitude of perturbed hydrographic profiles observed in the field (J. W. Lavelle et al., Effects of deep ocean hydrothermal discharge on near-source hydrography: Surrogate field studies with a convective plume model, Pacific Marine Environmental Laboratory contribution 1735, National Oceanic and Atmospheric Administration, Seattle, Washington, 1996).
Model content vis-a-vis the simpler entrainment model of Morton
et al. [1956] was examined by computing the effective entrainment coefficient
from axisymmetric convective plume results [Lavelle
and Baker, 1994]. Horizontal velocities at the stem wall were divided
by the average vertical velocity at the same height in the stem, and results
were profiled as a function of height from the buoyancy source. Entrainment
profiles so derived showed the entrainment coefficient having a magnitude comparable
to that customarily used with integral theory ( ~ 0.1). Contrary to the assumption of entrainment theory the entrainment coefficient
was not constant with height, even becoming negative in the plume cap region
[Lavelle
and Baker, 1994]. The number of model checks and comparisons to measurements
enumerated here demonstrates how well tested this convection model is.
~ 0.1). Contrary to the assumption of entrainment theory the entrainment coefficient
was not constant with height, even becoming negative in the plume cap region
[Lavelle
and Baker, 1994]. The number of model checks and comparisons to measurements
enumerated here demonstrates how well tested this convection model is.
Return to previous section or go to next section