" and thereby the Rossby wave speed, by up to about ±50%.
4.2.1. A Rossby wave model
Lacking data to diagnose the terms of the equations of motion directly, we examine solutions to simple models to evaluate their consistency with observations. If a simple model is able to reproduce the observed phenomena, there is no compelling justification for invoking more complex hypotheses. In situations where the simple model fails, it points to locations where other processes are active. The simplest first guess at the low-frequency, large-scale evolution of the off-equatorial thermocline is a model consisting only of long quasi-geostrophic Rossby waves forced by wind stress curl. This model adds elementary time dependence to the Sverdrup dynamics discussed in Section 4.1, allowing time-varying wind stress curl to pump the thermocline depth. It has been used by many investigators to interpret low-frequency variability in the tropical Pacific (Meyers, 1979; Kessler, 1990; Chen and Qiu, 2004).
Rossby waves are due to the latitudinal change in the local vertical component of the earth's rotation (zero at the equator, f/2 at the poles). Consider a symmetric hump of sea level, forced externally (say by downwelling wind stress curl). The geostrophic flow around the hump is westward on the equatorward side and eastward on the poleward side (like the Tehuantepec Bowl). However, because of the variation of f, flow on the equatorial side is stronger than that on the poleward side, thus more water is being transported westward than eastward. The result of this is to pile up water on the west side of the hump, and remove water from the east side. Therefore, the hump moves west from its initial position. That net transport is what makes a Rossby wave propagate west (and note that the westward propagation occurs equally well for a sea level depression, with the sense of the currents reversed). Because the difference in f across a hump of a given size is larger near the equator, the Rossby speed is much larger in the tropics.
The simple model has several potential weaknesses. By its neglect of velocity acceleration terms, the model excludes the near-equatorial waves that would be essential to study the region less than about ±3–4° latitude, but it has proven useful in the tropics (Kessler, 1990). By its neglect of nonlinear terms, the model excludes the advection of vorticity that has been shown to be important near the equatorial undercurrent (Kessler et al., 2003; and see Niiler, 2001 for estimates of these terms in the eastern tropical Pacific) and which may play a role near the narrow jet around the southeast corner of the Costa Rica Dome. The full range of effects of the nonlinear terms is not well understood; one likely consequence would be to change the "effective " and thereby the Rossby wave speed, by up to about ±50%.
The model can be written:
where h is the thermocline depth anomaly (positive down), 
is the wind stress and 
the density of seawater. The long Rossby wave speed is c
= -c
/f (c is the internal long gravity wave speed, f is the Coriolis parameter and its meridional derivative), and R is a damping timescale. Note that f is now allowed to vary with latitude. The two parameters to be chosen are the gravity wave speed c, which is estimated to be between 2 and 2.5 m s
in the eastern tropical Pacific (Chelton et al., 1998), and the damping timescale R, typically taken to be (6–12 months) (Picaut et al., 1993). Here we choose c = 2 m s and R = (9 months); in fact the results are qualitatively insensitive to these choices within the reasonable ranges 1.75 m s ≤ c ≤ 3 m s and R ≤ (2 years). Additional realism could perhaps be achieved by choosing a different gravity speed c at each latitude, or by letting c be a function of longitude as well, but this did not seem necessary for the present purposes of making a first guess at the importance of the linear response to wind forcing. Solutions to the model encompass the local forcing by wind stress curl plus the subsequent westward propagation of any anomalies created.
Since long Rossby waves propagate non-dispersively due west, the wind-driven solution can be written separately at each latitude as an integral in x that sums the contributions of the wind forcing on the wave as it travels westward at speed c:
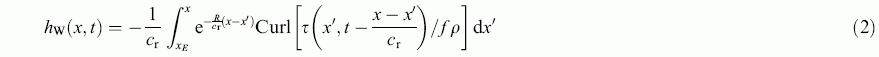
where h
(x, t) is the interior wind-driven part of h. Note that Curl(/f ) in (2) is evaluated not at time t but at previous times looking back along the wave ray at speed c, that is, at times t - (x - x
)/c. The lower limit of integration x
is the longitude of the eastern boundary, and because the integration is westward, dx is negative.
Rossby waves can also radiate from the eastern boundary (for instance due to reflection of equatorial Kelvin waves), and these influences must be added to the interior solution (2):
where h
is the damped effect of eastern boundary signals propagating to the interior. As done for the curl in (2), the value of h at the eastern boundary (h) is evaluated at previous times reflecting the lag for propagation from x to x.
The complete solution h to (1) is h from (2) plus h from (3); these are solved at each latitude independently and then combined. Here we use the average annual cycle of the ERS winds (see Appendix B) to force (2), and the eastern boundary value of observed 20 °C depth from the XBT data as h in (3). Solutions to (1) have also been found using other scatterometer winds (Quikscat) and from in situ wind products (FSU; see Appendix B) for various time periods, and the results are not strongly dependent on the wind data set used. In principle, a solution could be obtained entirely from the wind forcing, without the use of any ocean initialization along the boundary, using a basin-wide model to account for the generation of equatorial Kelvin waves, which may be forced by winds anywhere along the equator, or by western boundary reflections of Rossby waves. However, it is unclear how useful a single-baroclinic-mode model is over very long distances (e.g., Kessler and McCreary, 1993). In addition, observed near-coastal thermocline anomalies propagate poleward along the American coast very much slower than the coastal Kelvin waves a single-mode model would predict (Enfield and Allen, 1980; Chelton and Davis, 1982; Spillane et al., 1987; Pizarro et al., 2001; Strub and James, 2002c), so a purely wind-driven model clearly requires a realistic shelf structure and more complete baroclinicity (e.g., Clarke and Ahmed, 1999). Since we are interested here only in the eastern region and in the effects of wind stress curl, it seemed more appropriate to use the available information about the actual fluctuations along the boundary, rather than try to derive them from a model. In fact the boundary contribution to the total is small, except close to the coast, though it is noted that this contribution is essential in diagnosing changes in the coastal currents like the WMC, which depend on the offshore gradient.
The results of the Rossby model are compared to observed 20 °C depth anomalies in Fig. 10, for four average seasons. The solution can be thought of as a combination of westward-propagating Rossby waves forced by wind stress curl that seesaws annually across a nodal line at 8°N. The sum of the wave plus the local forcing appears as a generally southwestward phase propagation with wave crests approximately parallel to the Central American coast. (However, in fact the phase propagates purely westward at each latitude; the apparent meridional propagation occurs because the wind stress curl forcing oscillates so strongly out of phase across a nodal line at about 8°N, and the solution combines both local forcing and wave propagation.) In both the Rossby model and the observations, signals appear to originate as a thin region near the coast, grow and separate from the coast, and finally leave the region at the southwest corner. In general the model represents the magnitude and position of the observed thermocline signals reasonably well, though there is a sense that the model propagation is too slow at the northern edge and too fast at the southern (e.g., Kessler, 1990). It might be possible to improve this by varying the gravity wave speed c, but it seems useful to appreciate how well even the simplest type of model represents reality with minimum tuning.
A difference between model and observations is that the model solution depicts particular latitudes as having strong maxima, while the observations are smoother (Fig. 10). Since the model solutions are entirely independent at each latitude, its results are sensitive to narrow areas of strong wind stress curl, especially those associated with the mountain-gap wind jets (note the three positive maxima extending westward from the Tehuantepec, Papagayo and Panama jet outflow regions in the model JFM season). In reality, energetic eddies generated by the wind jets (but not represented in the linear model) produce horizontal mixing that blends latitudes together.
There is little indication of the features of the mean thermocline topography in the observed annual cycle anomalies (Fig. 10, left panels). No signatures of the mean ridges and troughs can be seen, nor of the Costa Rica Dome, nor of the regions of strong eddy activity. Instead the observations show a smooth southwestward propagation right across the strong thermocline topography and current shears. The good agreement with the model solution, which assumes a flat background thermocline (by the choice of a single value for c), with no eddy mixing, is evidence for the major role played by the linear response to wind forcing in the evolution of the annual cycle.
For the case of the Costa Rica Dome, the model correctly depicts the sequence of uplifting beginning at the coast early in the year, westward growth and separation in April–May–June, and strengthening of the ridge to the west of the dome in boreal summer-fall, as described by Fiedler (2002). Like the observations, the magnitude of thermocline depth variability at the dome is smaller than to its west; less than ±5 m compared to at least twice that further west (Fig. 10). The shoaling and extension of the dome into the Gulf of Tehuantepec in boreal fall is also evident in the linear model (lower right panels of Figs. 7 and 10). Similarly, the model correctly depicts the cutting-off of this bump in winter.
For the case of the NECC, the model shows that observed deepening along the 10°N ridge near 110°W in April–May–June that weakens the NECC (Fig. 7, lower left) is consistent with the wind forcing and Rossby wave propagation (Fig. 10, second row). In boreal fall the wind-forced Rossby wave produce the opposite anomalies (Fig. 10, bottom row), and the NECC strengthens (Fig. 7, lower right).
As noted above, it might well be thought that the climatological Tehuantepec Bowl simply reflects aliased sampling of the strong anticyclonic eddies that are due to the Tehuantepec winter wind jet (Willett et al., 2006). In that case one would expect that the linear Rossby wave model would not represent this feature very well. However, the model solution in fact captures the seasonal evolution of the bowl quite realistically, suggesting that its boreal winter-spring deepening is due to downwelling curl associated with the western side of the Tehuantepec wind jet, and the boreal summer shoaling is due to the upwelling curl from the eastern side of the jet that arrives later (Fig. 10, top and upper middle set of panels). The downwelling curl from Tehuantepec extends over the eastern part of the bowl (e.g., Fig. 1), so this is felt during immediately, during winter and soon after. By boreal spring, the downwelling Rossby wave extends past the west side of the bowl (Fig. 10, upper middle panels), establishing the connection to the basin-wide thermocline trough along 15°N (Fig. 7, lower left). However, the upwelling signal from the east side of the wind jet takes about 6 months to propagate to 105°W (at the relatively slow Rossby wave speed of 190 km month at 14°N), weakening the bowl in summer. Though the region just west of the Gulf of Tehuantepec that is strongly affected by the winter eddies might be expected to be a place where linear dynamics are least appropriate, the good correspondence of the simple model with reality shows that not to be the case.
Along the Central American coast, observed 20 °C depth anomalies suggest a poleward propagation with deep thermocline found at about 10°N in boreal winter, then moving along the southwest coast of Mexico in summer, arriving at the Gulf of California at the end of the year (Fig. 10, left panels). This is similar to the sequence shown from satellite altimetry by (Strub and James (2002b), see their Fig. 6), who show that this signal apparently stretches north to the coast of California. The mechanism of propagation remains unknown. Since the anomaly has a narrow offshore scale (a few hundred kilometers), the zonal gradient it produces results in poleward transport anomalies along the coast of Mexico (strengthening the WMC) during boreal summer and fall.
We can conclude from the Rossby model comparisons that these simple dynamics gives a good first-order picture of the annual cycle evolution in the northeastern tropical Pacific. The large-scale features of the regional evolution are principally explained by a linear ocean response to wind forcing, despite the evident possibilities of a fundamental role for the energetic eddies and their more complex dynamics. That means, for example, that one should not see the annual cycle of the Costa Rica Dome as an isolated phenomenon. Instead, the westward growth of the dome and its separation from the coast reflect the passage of the regional-scale Rossby wave seen in Fig. 10. Discrepancies are found in the model wave being broken into specific latitude bands while the observations are smoothly connected across latitudes; presumably this would be improved by a model that additionally allowed communication across latitudes by horizontal eddy mixing, as occurs in the ocean.
Return to previous section or go to next section
