U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
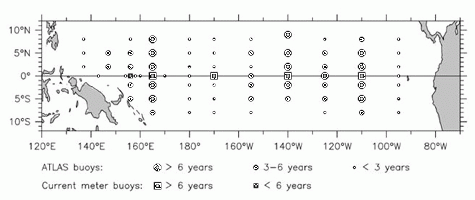
Figure 1. The TOGA-TAO buoy array as of September 1993, showing the approximate length of time the various buoys have been in the water. The present study uses principally the long-term thermistor chain buoys and the current meter buoys, which have been operating for 5 years or longer.
Figure 2. Buoy sampling diagram at 0°, 140°W, showing the history of observations at this location at the various depths sampled. Note that only a few depths have continuous sampling over the 10 years of operation. The overlay of 20°C depth (filtered with a 121-day triangle (dark), and 17-day triangle (light)) shows that this value can be reliably calculated by vertical interpolation with no gaps even though temperature at any of the fixed levels would be gappy.
Figure 3. Longitude-time plot of 20°C depth on the equator. The contours and shading show the depth of the 20°C isotherm, zonally interpolated between the buoy positions (see text). Contour interval is 20 m, and deeper thermocline depths are darker shades. The slanted lines show identified downwelling Kelvin wave ray paths (see text) and represent a speed of 2.4 m s-1. The heavy line at top shows the time series of zonal winds averaged over 165°E-180° (scale at upper right). Both time series have been smoothed with a 17-day triangle filter (see text).
Figure 4. Longitude-time plot of zonal winds on the equator. The plot has the same format as Figure 3 for 20°C depth. The contours and shading show the zonal wind at a contour interval of 3 m s-1. Westerlies are darker shades. The heavy curve at top show the time series of OLR averaged between 160°E and 170°E on the equator, with values below 220 W m-2 darkened (scale at upper right). Both time series have been smoothed with a 17-day triangle filter.
Figure 5. Longitude-time plot of SST on the equator. The plot has the same format as Figures 3 and 4. The contours and shading show the SST (actually, the 1-m temperature) at a contour resolution of 1°C, with supplementary shading at 29.5°C. Darker shades show warmer SST. The slanted lines are the same Kelvin wave paths shown in Figure 3.
Figure 6. Variance-preserving spectra of OLR at 165°E, zonal wind at 165°E, 20°C depth at 140°W, and equatorial undercurrent speed at 140°W, 120 m depth, all at the equator. Each variable has a separate scale as indicated. The spectra are calculated for the 10-year period April 1983-April 1993 for all quantities except the zonal wind, for which only the 7 years July 1986-July 1993 are available.
Figure 7. Squared coherence amplitude of OLR at 165°E, zonal wind at 165°E and zonal current at 140°W with 20°C depth at 140°W; 95% confidence levels are indicated by the thin horizontal lines, which also show the frequency bands used to smooth the raw periodograms (see text).
Figure 8. Squared coherence amplitude (top) and phase (bottom) of OLR at 90°E with 20°C depth at 140°W. The intraseasonal peak is centered at 74 days. Positive phase indicates deep 20°C depth leads low OLR. (Top) 95% confidence limits on the coherence amplitude are shown by the thin horizontal lines; 95% confidence limits on the phase are shown as "error bars," in each of the five frequency intervals in which the coherence (top panel) is significant above the 95% level. The phase limits are an average over each such interval and are plotted at the center of the intervals.
Figure 9. Squared coherence amplitude and phase of 20°C depth over the zonal extent of the buoy array with that at 140°W, averaged in the frequency band 55-65 days. The solid line shows the coherence amplitude (identically 1 at 140°W), and the light dashed horizontal line is the 95% confidence level (scale at left). The heavy dashed line is the phase, expressed as a lag in days with the phase at 140°W (scale at right). The thin solid line along the phase is a best fit straight line to the phase and represents a speed of 2.43 m s-1. This fit is the basis for the slope of the slant lines in Figures 3 and 5.
Figure 10. Time-varying amplitude of the intraseasonal variability obtained through complex demodulation of (a) 20°C depth at 0°, 140°W, (b) zonal winds at 165°E, and (c) OLR at 165°E. The demodulation is performed about a central frequency of 60 days, with half-power between 42 and 108 days. The dashed line overlaid is a 1-year running mean of each demodulated time series.
Figure 11. Average year of 60-day amplitude of 20°C depth at 0°, 140°W (meters, solid line, scale at left; data from Figure 10a), zonal winds at 165°E (meters per second, dashed line, scale at right; data from Figure 10b) and OLR at 165°E (W m-2, dotted line, scale at left; data from Figure 10c).
Figure 12. (a) Detail of SST on the equator for July 1991 through April 1992 (during the peak of the El Niño of 1991-1992). Contours and shading show SST with a contour interval of 1°C, with supplemental contour/shade at 29.5°C. Light contours show warmer temperatures (opposite of Figure 5). The heavy slant lines are the same Kelvin lines shown in Figure 3. The heavy contour labeled "0" is the zero line of zonal winds, showing the steplike progression of westerlies eastward over the Pacific during the onset of the warm event. (b) Model SST/wind to match the timing of Figure 12a. Output of the simple model described in section 4. The heavy curve is the eastern edge of the 29°C SST and the wind patch (the result of integrating (3); see text). The light sinusoidal curve at top is the time series of winds from (1) (up is easterly, down is westerly) (winds are zero before day 0). The shading shows the region of westerly winds. Slant lines indicate maximum positive pressure perturbation to match the observed Kelvin lines in Figure 12a; east of the forced region these are Kelvin characteristics, within the forced region they move at speed 2c (see text).
Figure 13. Comparison of d(SST)/dt and ud(SST)/dx at 0°, 140°W. The solid line shows -ud(SST)/dx, where u is taken as the 14-m (shallowest level) zonal current measured by ADCP and d(SST)/dx is estimated by centered difference between 125°W and 155°W. The dashed line is d(SST)/dt at 140°W. Both time series are filtered with a 17-day triangle filter. Upward on the plot indicates a warming tendency for both time series.
Figure 14. Complex (frequency domain) EOF 1 of intraseasonal (30- to 80-day period) OLR along the equator in the Pacific during 1979-1993. (Top) Amplitude (W m-2) of the complex eigenvector. The zonal structure of this EOF is used to estimate the zonal length of the OLR patch (see text). (Middle) Phase relative to 125°E. The slope in the western Pacific indicates eastward propagation at a speed of about 4.5 m s-1. (Bottom) Percent variance represented.
Figure 15. Theoretical variance of zonal current east of a 5000-km width wind patch, calculated according to (6), shown as a function of forcing frequency. The top axis numbering shows the periods in days. Note the rapid drop in variance between 100-day and 30-day periods.
Return to References or go back to Abstract