U.S. Dept. of Commerce / NOAA / OAR / PMEL
/ Publications
Interior pycnocline flow from the Subtropical to the Equatorial
Pacific Ocean
Gregory C. Johnson and Michael J. McPhaden
NOAA, Pacific Marine Environmental Laboratory, 7600 Sand Point
Way NE, Seattle, Washington 98115-6349
Journal of Physical Oceanography, 29, 3073–3089, 1999.
This paper is not subject to U.S. copyright. Published in 1999 by the American
Meteorological Society
5. Interior quasi-meridional geostrophic mass transport estimates
Geostrophic calculations are made relative to a reference surface of 900 dbar,
roughly  n = 27.5 kg m
n = 27.5 kg m .
Inspection of the depth of this isopycnal (not shown) suggests that geostrophic
shear at this surface is weak except in the far southwest portion of the region
under investigation, where the subtropical pycnocline is deep. This assumption
is supported by direct measurements at this level (Davis
1998). The 900-dbar surface sits well beneath the tropical pycnocline and
its use as a reference surface captures all the geostrophic shear above. Three
previous quantitative works on zonal mass transports across the Tropics used
similar surfaces: 600 dbar at 165°E (Gouriou
and Toole 1993), 1000 dbar between 150°W and 158°W (Wyrtki
and Kilonsky 1984), and 500 dbar at 110°W (Hayes
et al. 1983).
.
Inspection of the depth of this isopycnal (not shown) suggests that geostrophic
shear at this surface is weak except in the far southwest portion of the region
under investigation, where the subtropical pycnocline is deep. This assumption
is supported by direct measurements at this level (Davis
1998). The 900-dbar surface sits well beneath the tropical pycnocline and
its use as a reference surface captures all the geostrophic shear above. Three
previous quantitative works on zonal mass transports across the Tropics used
similar surfaces: 600 dbar at 165°E (Gouriou
and Toole 1993), 1000 dbar between 150°W and 158°W (Wyrtki
and Kilonsky 1984), and 500 dbar at 110°W (Hayes
et al. 1983).
Quasi-meridional interior geostrophic mass transport estimates presented here
are made in a layer extending from the base of the mixed layer to the base of
the tropical pycnocline. The results are similar to those inferred independently
from wind fields using Sverdrup dynamics (McPhaden
and Fine 1988), but here the magnitudes of the interior meridional transports
are quantified as well as the density range over which they occur. The mixed
layer is excluded because the mean wind field over nearly the entire region
dictates a poleward Ekman transport (Lu
and McCreary 1995), which overwhelms the equatorward geostrophic velocity
in the mixed layer. Our functional definition of the tropical pycnocline base
in this instance is the neutral density at which the net interior meridional
mass transport changes sign from equatorward above to poleward below within
a 9° latitude band containing the deep cyclonic gyres in each hemisphere.
In the Northern Hemisphere, from 3° to 11°N, the base sits at  n
= 25.9 ± 0.2 kg m
n
= 25.9 ± 0.2 kg m . In the southern
hemisphere, from 4 to 12°S, the base sits at
. In the southern
hemisphere, from 4 to 12°S, the base sits at  n
= 26.2 ± 0.2 kg m
n
= 26.2 ± 0.2 kg m (see Fig.
1 for isopycnal winter outcrop locations). Interior meridional transports
at 8°N and 8°S show convergent equatorward flow, hence interior communication
from the subtropics to the equator above these isopycnals and divergent poleward
flow in the deep cyclonic gyres below them (Fig.
6). Only interior transports are presented here. While western boundary
currents in both hemispheres transport significant amounts of subtropical pycnocline
water toward the equator, they have been extensively discussed elsewhere (Tsuchiya
et al. 1989; Lukas
et al. 1991; Butt
and Lindstrom 1994; Wijffels
et al. 1995).
(see Fig.
1 for isopycnal winter outcrop locations). Interior meridional transports
at 8°N and 8°S show convergent equatorward flow, hence interior communication
from the subtropics to the equator above these isopycnals and divergent poleward
flow in the deep cyclonic gyres below them (Fig.
6). Only interior transports are presented here. While western boundary
currents in both hemispheres transport significant amounts of subtropical pycnocline
water toward the equator, they have been extensively discussed elsewhere (Tsuchiya
et al. 1989; Lukas
et al. 1991; Butt
and Lindstrom 1994; Wijffels
et al. 1995).

Figure 6. Net meridional mass transport (10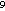 kg s
kg s ) excluding the mixed layer binned
in
) excluding the mixed layer binned
in  n every 0.2 kg m
n every 0.2 kg m from the South American coast to (a) 165°E at 8°S and (b) 135°E
at 8°N. In the south, equatorward flow is concentrated near the eastern
STMW density and poleward flow below
from the South American coast to (a) 165°E at 8°S and (b) 135°E
at 8°N. In the south, equatorward flow is concentrated near the eastern
STMW density and poleward flow below  n
= 26.1 kg m
n
= 26.1 kg m . In the north, equatorward
flow is at lighter densities and poleward flow below
. In the north, equatorward
flow is at lighter densities and poleward flow below  n
= 25.9 kg m
n
= 25.9 kg m . (c) Downward accumulated
integrals of (a) and (b) show the net interior transport within the pycnocline
(to
. (c) Downward accumulated
integrals of (a) and (b) show the net interior transport within the pycnocline
(to  n roughly 26 kg m
n roughly 26 kg m )
in the northern hemisphere (6 × 10
)
in the northern hemisphere (6 × 10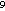 kg
s
kg
s ) is much less than that in the southern
hemisphere (14 × 10
) is much less than that in the southern
hemisphere (14 × 10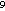 kg s
kg s ).
).
In the Southern Hemisphere, meridional mass transport estimates within the
pycnocline, from  n = 26.2
kg m
n = 26.2
kg m to the base of the mixed layer, are
made from 17°S equatorward. South of 17°S data starts too far off
the South American coast for a meaningful interior meridional transport estimate.
At all latitudes the interior meridional transport ends well east of the western
boundary, and equatorward of 14°S this transport starts west of South America.
The interior transport occurs between 135°W and South America at 17°S,
but shifts westward toward the equator and is found between 170°W and 110°W
by 6°S. Between 17°S and 6°S the estimates have a minimum of
13 (± 5) × 10
to the base of the mixed layer, are
made from 17°S equatorward. South of 17°S data starts too far off
the South American coast for a meaningful interior meridional transport estimate.
At all latitudes the interior meridional transport ends well east of the western
boundary, and equatorward of 14°S this transport starts west of South America.
The interior transport occurs between 135°W and South America at 17°S,
but shifts westward toward the equator and is found between 170°W and 110°W
by 6°S. Between 17°S and 6°S the estimates have a minimum of
13 (± 5) × 10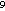 kg s
kg s at 9°S and a maximum of 19 (± 2) × 10
at 9°S and a maximum of 19 (± 2) × 10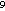 kg s
kg s at 16°S, both latitudes where
data are sparse and error estimates are large. From 17°S to 6°S the
weighted average and standard deviation of interior meridional mass transport
is 15 (± 1) × 10
at 16°S, both latitudes where
data are sparse and error estimates are large. From 17°S to 6°S the
weighted average and standard deviation of interior meridional mass transport
is 15 (± 1) × 10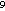 kg s
kg s (Fig. 7a). This value is an estimate of the interior
subtropical mass transport from the Southern Hemisphere toward the equator.
For purposes of comparison, this interior meridional mass transport estimate
slightly exceeds the 9–12 (× 10
(Fig. 7a). This value is an estimate of the interior
subtropical mass transport from the Southern Hemisphere toward the equator.
For purposes of comparison, this interior meridional mass transport estimate
slightly exceeds the 9–12 (× 10 m
m s
s )
of southern origin estimated to join the EUC core from western boundary currents
in the Southern Hemisphere (Butt
and Lindstrom 1994). These results are in reasonable accord with analysis
of a data assimilation product which suggest western boundary and interior transports
at 10°S of 15 and 11 (× 10
)
of southern origin estimated to join the EUC core from western boundary currents
in the Southern Hemisphere (Butt
and Lindstrom 1994). These results are in reasonable accord with analysis
of a data assimilation product which suggest western boundary and interior transports
at 10°S of 15 and 11 (× 10 m
m s
s ), respectively (Huang
and Liu 1999).
), respectively (Huang
and Liu 1999).

Figure 7. Quasi-meridional interior pycnocline (mixed-layer base to pycnocline
base) mass transport (10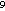 kg s
kg s )
zonally accumulated from the Americas westward. Symbols are individual integration
points and lines are objectively mapped assuming a Gaussian covariance with
a correlation length scale of 20° longitude and an error-to-signal energy
of 0.25. (a) Southern hemisphere transports at three latitudes (17°S solid
line, 12°S dashed, and 7°S dot-dashed) with a pycnocline base at
)
zonally accumulated from the Americas westward. Symbols are individual integration
points and lines are objectively mapped assuming a Gaussian covariance with
a correlation length scale of 20° longitude and an error-to-signal energy
of 0.25. (a) Southern hemisphere transports at three latitudes (17°S solid
line, 12°S dashed, and 7°S dot-dashed) with a pycnocline base at  n
= 26.2 kg m
n
= 26.2 kg m . (b) Northern hemisphere transport
between the NEC and NECC with a pycnocline base at
. (b) Northern hemisphere transport
between the NEC and NECC with a pycnocline base at  n
= 25.9 kg m
n
= 25.9 kg m . (c) Northern hemisphere transport
between the NECC and SEC with a pycnocline base at
. (c) Northern hemisphere transport
between the NECC and SEC with a pycnocline base at  n
= 25.9 kg m
n
= 25.9 kg m .
.
Equatorward of 6°S, meridional interior transport estimates increase from
20 (± 2) × 10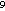 kg s
kg s between 170°W and 110°W at 5°S to 30 (± 4) × 10
between 170°W and 110°W at 5°S to 30 (± 4) × 10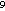 kg s
kg s between 170°W and 120°W
at 3°S. While low-latitude geostrophic calculations are noisy, the trend
is clear. This rapid increase probably reflects the presence of a shallow meridional
overturning cell at the equator, with interior equatorward geostrophic transport
working to offset large poleward mass transports in the Ekman layer. This cell
has been observed in profiling and acoustic Doppler current meter data from
the Hawaii-Tahiti Shuttle Experiment (McPhaden
1984; Johnson
and Luther 1994) and reproduced in numerical models (Lu
et al. 1998).
between 170°W and 120°W
at 3°S. While low-latitude geostrophic calculations are noisy, the trend
is clear. This rapid increase probably reflects the presence of a shallow meridional
overturning cell at the equator, with interior equatorward geostrophic transport
working to offset large poleward mass transports in the Ekman layer. This cell
has been observed in profiling and acoustic Doppler current meter data from
the Hawaii-Tahiti Shuttle Experiment (McPhaden
1984; Johnson
and Luther 1994) and reproduced in numerical models (Lu
et al. 1998).
The Northern Hemisphere is somewhat more complicated than the Southern Hemisphere,
with the quasi-zonal NEC, NECC, SEC, and EUC alternating in flow direction.
Instead of presenting simple meridional mass transports, which would contain
portions of these quasi-zonal currents, we isolate the cross-gyre transports
by calculating transports across the geopotential anomaly trough under the ITCZ
that separates the NEC from the NECC (Fig. 7b).
Another estimate is made across the lower-latitude ridge that separates the
NECC from the SEC and 2°N at a few western longitudes where no ridge is
evident (Fig. 7c). In both cases, there are regions
of little net transport east and west of where the interior meridional transport
occurs. Within the pycnocline, from  n
= 25.9 kg m
n
= 25.9 kg m to the base of the mixed layer,
–5 (± 1) × 10
to the base of the mixed layer,
–5 (± 1) × 10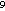 kg s
kg s flows across the trough from the NEC to the NECC between 165°E and 135°W.
This value is an estimate of the interior subtropical mass transport from the
Northern Hemisphere toward the equator, and is one third the estimate of 15
(± 1) × 10
flows across the trough from the NEC to the NECC between 165°E and 135°W.
This value is an estimate of the interior subtropical mass transport from the
Northern Hemisphere toward the equator, and is one third the estimate of 15
(± 1) × 10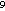 kg s
kg s equatorward interior flow estimated for the Southern Hemisphere. A simple comparison
of interior pycnocline meridional mass transports along 8°N and 8°S
gives a similar result (Fig. 6c). The Northern
Hemisphere interior transport estimate is probably an upper bound because it
may contain southward flow from a tropical recirculation around the ITCZ centered
near 11°N, 125°W (Fig. 2b). However,
since there is no evidence of any significant northward component of the recirculation
east of 125°W (Fig. 7b), the net tropical
recirculation is likely to be small. For purposes of comparison, this northern
interior transport is less than half of the 13–16 (× 10
equatorward interior flow estimated for the Southern Hemisphere. A simple comparison
of interior pycnocline meridional mass transports along 8°N and 8°S
gives a similar result (Fig. 6c). The Northern
Hemisphere interior transport estimate is probably an upper bound because it
may contain southward flow from a tropical recirculation around the ITCZ centered
near 11°N, 125°W (Fig. 2b). However,
since there is no evidence of any significant northward component of the recirculation
east of 125°W (Fig. 7b), the net tropical
recirculation is likely to be small. For purposes of comparison, this northern
interior transport is less than half of the 13–16 (× 10 m
m s
s )
of northern origin water estimated to reside within the core of the EUC well
to the west at 153°E (Butt
and Lindstrom 1994). These results are again in reasonable accord with analysis
of a data assimilation product, which suggests western boundary and interior
transports at 10°N of 14 and 3 × 10
)
of northern origin water estimated to reside within the core of the EUC well
to the west at 153°E (Butt
and Lindstrom 1994). These results are again in reasonable accord with analysis
of a data assimilation product, which suggests western boundary and interior
transports at 10°N of 14 and 3 × 10 m
m s
s ,
respectively (Huang
and Liu 1999).
,
respectively (Huang
and Liu 1999).
Farther to the south, an estimated –35 (± 8) × 10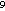 kg s
kg s flows across the low-latitude ridge
from the NECC to the SEC between 165°E and 105°W (Fig.
7c). The 30 (± 8) × 10
flows across the low-latitude ridge
from the NECC to the SEC between 165°E and 105°W (Fig.
7c). The 30 (± 8) × 10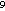 kg s
kg s increase in equatorward transport with relation to the northern estimate seems
large and may be an upper bound, since part of the transport calculation is
made at 2°N, a fairly low latitude at which to apply geostrophy. However,
this increase can fairly easily be accounted for by a combination of two similarly
sized sources. First, the addition of northern subtropical water from the Mindanao
Current (Lukas
et al. 1991; Wijffels
et al. 1995) at the western boundary transported eastward within the NECC
could be contributing to equatorward pycnocline mass flux. The NECC carries
20 × 10
increase in equatorward transport with relation to the northern estimate seems
large and may be an upper bound, since part of the transport calculation is
made at 2°N, a fairly low latitude at which to apply geostrophy. However,
this increase can fairly easily be accounted for by a combination of two similarly
sized sources. First, the addition of northern subtropical water from the Mindanao
Current (Lukas
et al. 1991; Wijffels
et al. 1995) at the western boundary transported eastward within the NECC
could be contributing to equatorward pycnocline mass flux. The NECC carries
20 × 10 m
m s
s at 165°E (Gouriou and Toole 1993)
and only 8 × 10
at 165°E (Gouriou and Toole 1993)
and only 8 × 10 m
m s
s by 110°W (Hayes et al. 1983), allowing
for an increase of 12 × 10
by 110°W (Hayes et al. 1983), allowing
for an increase of 12 × 10 m
m s
s in equatorward transport from the NECC
to the SEC. Second, the poleward Ekman transport across the low-latitude ridge
is 45 × 10
in equatorward transport from the NECC
to the SEC. Second, the poleward Ekman transport across the low-latitude ridge
is 45 × 10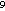 kg s
kg s between 165°E and 105°W using the Hellerman
and Rosenstein (1983) surface wind stress climatology after applying a recommended
scaling factor of 0.8 to correct the drag coefficient (Harrison
1989). If 40 (± 25)% of the equatorward geostrophic transport balancing
this Ekman transport occurs in a shallow tropical meridional cell extending
below the mixed layer (Lu
et al. 1998), it would account for the remaining mass budget within interior
meridional transport errors.
between 165°E and 105°W using the Hellerman
and Rosenstein (1983) surface wind stress climatology after applying a recommended
scaling factor of 0.8 to correct the drag coefficient (Harrison
1989). If 40 (± 25)% of the equatorward geostrophic transport balancing
this Ekman transport occurs in a shallow tropical meridional cell extending
below the mixed layer (Lu
et al. 1998), it would account for the remaining mass budget within interior
meridional transport errors.
Return to previous section or go to next
section
PMEL Outstanding Papers
PMEL Publications Search
PMEL Homepage
 n = 27.5 kg m
n = 27.5 kg m .
Inspection of the depth of this isopycnal (not shown) suggests that geostrophic
shear at this surface is weak except in the far southwest portion of the region
under investigation, where the subtropical pycnocline is deep. This assumption
is supported by direct measurements at this level (Davis
1998). The 900-dbar surface sits well beneath the tropical pycnocline and
its use as a reference surface captures all the geostrophic shear above. Three
previous quantitative works on zonal mass transports across the Tropics used
similar surfaces: 600 dbar at 165°E (Gouriou
and Toole 1993), 1000 dbar between 150°W and 158°W (Wyrtki
and Kilonsky 1984), and 500 dbar at 110°W (Hayes
et al. 1983).
.
Inspection of the depth of this isopycnal (not shown) suggests that geostrophic
shear at this surface is weak except in the far southwest portion of the region
under investigation, where the subtropical pycnocline is deep. This assumption
is supported by direct measurements at this level (Davis
1998). The 900-dbar surface sits well beneath the tropical pycnocline and
its use as a reference surface captures all the geostrophic shear above. Three
previous quantitative works on zonal mass transports across the Tropics used
similar surfaces: 600 dbar at 165°E (Gouriou
and Toole 1993), 1000 dbar between 150°W and 158°W (Wyrtki
and Kilonsky 1984), and 500 dbar at 110°W (Hayes
et al. 1983). 
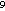 kg s
kg s ) excluding the mixed layer binned
in
) excluding the mixed layer binned
in  m
m s
s