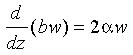 (2)
(2)U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
Constraints on the characteristics of the hydrothermal release resulting in a megaplume can be derived from models of turbulent buoyancy-driven convective fluids [e.g., Morton et al., 1956; Turner, 1973]. Models of this kind have already been employed for hydrothermal plumes [Converse et al., 1984; Middleton and Thompson, 1986; Little et al., 1987]. Such models propose that upward convection of the hydrothermal plume is forced by the density deficiency of the hot hydrothermal fluid with respect to the surrounding water. The deficiency in density is diminished over distance from the source by entrainment of ambient water into the plume. Eventual complete quenching of the density deficiency in a stably stratified environment limits the height of rise of the plume. The observed height of rise can be used to infer the value of the heat flux at the vent. In the model presented below we specifically apply these concepts to the megaplume observations. The computations are based on an idealized plume source configuration and plume ascent, however, so the model results must be taken as suggestive rather than definitive.
The model assumes that the turbulent entrainment of ambient fluid is proportional to upward plume velocity, that profiles across the plume are similar at all heights (here top-hat profiles), and that the fluid is incompressible. Previous applications of such models to hydrothermal systems [Converse et al., 1984; Middleton and Thompson, 1986; Little et al., 1987] have addressed plumes arising from individual vents and have thus been confined to axisymmetric geometry, but for reasons to be indicated below, we choose to model a linear source and planar plume. Because of the near-radial symmetry of the observed plume cap, however, the source length must be small with respect to the diameter of the plume cap. End effects of a finite length source are not part of the model. On the basis of the development of Morton et al. [1956], the conservation equations for a two-dimensional plume are as follows: for mass,
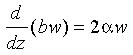 (2)
(2)
for momentum,
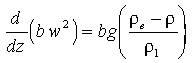 (3)
(3)
for heat,
![]() (4)
(4)
and for salinity,
![]() (5)
(5)
where b is the plume width (e.g., the distance across the linear source
fissure), w is the upward velocity, z is the vertical coordinate (positive
upward),  is the entrainment coefficient, g is the
acceleration of gravity,
is the entrainment coefficient, g is the
acceleration of gravity,  is the density in the plume, S
and T are the salinity and temperature, respectively, Cp is the specific heat of salt water at constant
pressure, and Q is the heat content per unit volume of the plume. Qe, Te, Se, and ρe refer to
properties in the ambient environment, and ρ1 is the ambient density at the plume source. The
heat content per unit volume, Q, and the temperature are related by
is the density in the plume, S
and T are the salinity and temperature, respectively, Cp is the specific heat of salt water at constant
pressure, and Q is the heat content per unit volume of the plume. Qe, Te, Se, and ρe refer to
properties in the ambient environment, and ρ1 is the ambient density at the plume source. The
heat content per unit volume, Q, and the temperature are related by
![]() (6)
(6)
Notice that the model employs an equation conserving heat rather than temperature because Cp (as does ρ) depends nonlinearly on T at high temperature [e.g., Little et al., 1987].
Because of the assumption of incompressibility, potential temperatures and density referenced to the source depth (~2300 m) were used throughout. For T < 40°C and S < 42‰, densities at 230 bars were taken from the formula for density of seawater given by Gill [1982]; densities at T > 40°C were interpolated from tables given by Potter and Brown [1977] and Burnham et al. [1969]. The specific heat of seawater at 230 bars varies from 4100 J kg−1 °K−1 to 6600 J kg−1 °K−1 over the temperature range 200°C to 350°C [Bischoff and Rosenbauer, 1985]. Below 200°C, Cp = 4100 J kg−1 °K−1. Ambient potential temperature and salinity profiles, taken from CTD casts in ambient water just outside megaplume 1, were fit between depths of 1000 m and 2300 m with quadratic curves.
The model equations were consequently integrated using initial values of T0 = 350°C and S0 = 34.63‰, the ambient salinity at 2300 m, for a range of mass fluxes. In all calculations, the coefficient of entrainment of ambient water into the buoyant plume was given a value of α = 0.1 based on laboratory experiments. For example, for two-dimensional plumes a range for α of 0.055 to 0.11 has been suggested [Kostsovinos and List, 1977; Wright and Wallace, 1979], the lower value for a pure jet and the upper value for a pure plume. For axisymmetric plumes, α values of 0.09 to 0.11 have been employed [Turner, 1973; Middleton and Thompson, 1986].
The axisymmetric analogs of (equations (2)–(6)) were evaluated first. To fulfill the observed megaplume 1 rise of 1025 m, vent diameters of approximately 4 m (vent exit velocity of 5 m/s) to 9 m (exit velocity of 1 m/s) would be required. This result did not change when the initial temperature of the vented fluids was varied over the range 325°–375°C because the nearly counterbalanced dependencies of density and specific heat on temperature makes the initial heat flux virtually constant. We judged such a spatially restricted source of fluids to be unlikely and turned instead to a model in which the source was a linear one (equations (2)–(6)), a geometric analog to seafloor fissures.
Equations (2)–(6) were consequently integrated under varying conditions of vent width and fluid exit velocities. The calculated heights of rise were found to depend on the heat flux at the vent (Figure 8) just as in the case of buoyancy-conserving, linearly stratified regimes [Turner, 1973]. To force a plume to the observed megaplume 1 rise height of ~1025 m requires a source heat flux of approximately 3.5 × 108 J/s per meter of vent fissure (Figure 8). The associated volume flux per unit length of the vent is 0.22 m3 m−1 s−1.
Figure 8. Relationship between plume rise height and the vent heat flux per meter of vent fissure for a linear plume with an entrainment coefficient of 0.1. The megaplume 1 rise height required a heat flux of ~3.5 × 108 J m−1 s−1.
The total excess heat in the megaplume, Qt , is the product of the length of the line source, ℓ, the duration of venting, τ, and the excess heat flux per unit length of source, Hh , entering the plume at height h:
![]() (7)
(7)
where the reference temperature is the ambient temperature at height h. Given a field-measured value of Qt and a model-estimated value for Hh , (7) can be inverted to determine the product of source length and duration.
Because there are no heat sources within the plume, Hh must be the sum of Hv, the excess heat flux per unit length at the plume base (vent flux), and Hc , the excess heat flux per unit length entrained laterally into the plume stem over the vertical distance zero to h. (Note that Hc is a negative heat flux because of the cooling effect of the upward entrainment of deep water.) Since 2αwdz is the volume flux per unit length laterally entrained at any height z (equation (2)), this sum may be written as
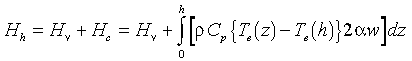 (8)
(8)
where Te(h) is the ambient potential temperature at height h. Equation (8) may also be derived by integrating (4) in z over the interval [0,h]. For high temperature vents, Hv is well approximated by the excess heat flux earlier estimated from plume rise height, the difference being that the ambient reference temperature in the two cases is taken at different locations (z = 0 and z = h).
The model constraint on τℓ thus takes the following form:
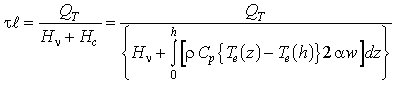 (9)
(9)
For megaplume 1, Qt is estimated to be 6.7 × 1016 J, and Hv is estimated to be 3.5 × 108 J m−1 s−1 as described earlier. The value of the integral in the denominator of (9) depends on the value given to h. If h = 700 m, then Hc = −1.6 × 108 J m−1 s−1. The resulting source strength τℓ is approximately 4000 m d. If h = 600 m, then τℓ = 3100 m d (Hc = −1.0 × 108 J m−1 s−1), and if h = 800 m, then τℓ = 6400 m d (Hc = −2.3 × 108 J m−1 s−1). The value for h of 700 m is our preferred choice because it represents the height above bottom of the vertical center of the plume (Figure 3).
Using a value of 4000 m d for ℓτ, the total volume and heat released during the megaplume 1 event were 7.6 × 107 m3 and 1.2 × 1017 J, respectively. (Both of these figures are about twice the preliminary estimates of Baker et al. [1987].) The comparative source strength for a megaplume 2-sized event is 1900 m d with a total volume and heat content of 3.6 × 107 m3 and 5.8 × 1016 J, respectively. From considerations of the megaplume 1 geometry and suspended particle population presented earlier, reasonable bounds on the duration of the causative venting event are 2–20 days. Consequently, from (9) with h = 700 m, the length of a venting fissure would be 2000–200 m.
Profiles of properties in the plume over the interval 1–1000 m from the source are shown in Figure 9 for the case of megaplumelike venting with an exit velocity of 2.5 m/s. The plume width remains relatively narrow for the first several hundred meters. Beyond that it rapidly enlarges. This is consistent with the observations that show the plume cap to begin several hundred meters from the seafloor. On the basis of laboratory studies of linear plumes in stratified environments, the thickness of the plume cap ought to be about one half the maximum height of the plume [Wallace and Wright, 1984]. In the case of these observations that would mean a plume cap thickness of ~500 m, not unlike the observations of ~700 m.
Figure 9. Vertical profiles of temperature (T), excess salinity (ΔS), plume width (b), and vertical velocity (w) for a linear plume with an exit velocity of 2.5 m/s.
Upward velocity in the plume (Figure 9) remains greater than 0.8 m/s to 700 m above bottom, after which it rapidly declines toward zero. A rough estimate of the rise time to maximum height is thus 20–30 min. These calculated velocities indicate that the plume would have no difficulty in lifting even the largest grains we observed in the filtered samples because their settling velocities are ~2 × 10−3 m/s. Temperature in the plume (Figure 9) falls off rapidly with height, decreasing to ~30°C at 10 m and ~6°C at 100 m. Excess salinity rises to ~0.1‰ near the top of the plume, reflecting the transport of salt in the plume from the more saline water at depth.
Go back to previous section or forward to next section