And thorough this distemperature we see the seasons alter...
Shakespeare's "A Midsummer Night's Dream"
Act 2, Scene 1
El Niño (EN) is characterized by a large-scale weakening of the trade winds and warming of the surface layers in the eastern and central equatorial Pacific Ocean. El Niño events occur irregularly at intervals of roughly 2–7 years, although the average is about once every 3–4 years [Quinn et al., 1987]. They typically last 12–18 months, and are accompanied by swings in the Southern Oscillation (SO), an interannual seesaw in tropical sea level pressure between the eastern and western hemispheres [Walker, 1924]. During El Niño, unusually high atmospheric sea level pressures develop in the western tropical Pacific and Indian Ocean regions, and unusually low sea level pressures develop in the southeastern tropical Pacific. Bjerknes [1966, 1969] was the first to link swings in the Southern Oscillation to El Niño events, proposing that the two phenomena were generated by coupled ocean-atmosphere interactions. SO tendencies for unusually low pressures west of the date line and high pressures east of the date line have also been linked to periods of anomalously cold equatorial Pacific sea surface temperatures (SSTs) sometimes referred to as La Niña [Philander, 1990]. The full range of SO variability, including both anomalously warm and cold equatorial SSTs, is often referred to as ENSO.
ENSO is associated with shifts in the location and intensity of deep convection and rainfall in the tropical Pacific. During El Niño events, drought conditions prevail in northern Australia, Indonesia, and the Philippines, and excessive rains occur in the island states of the central tropical Pacific and along the west coast of South America. Shifts in the pattern of deep convection in the tropical Pacific also affect the general circulation of the atmosphere and extend the impacts of ENSO to other tropical ocean basins and to midlatitudes [Rasmusson and Wallace, 1983; Ropelewski and Halpert, 1986, 1987; Halpert and Ropelewski, 1992; Trenberth et al., this issue]. During El Niño most of Canada and the northwestern United States tend to experience mild winters, and the states bordering the Gulf of Mexico tend to be cooler and wetter than normal. California has experienced a disproportionate share of episodes of heavy rainfall during El Niño winters such as 1982–1983, 1991–1992, and 1994–1995. Atlantic hurricanes tend to be less frequent during warm events and more frequent during cold events [Gray et al., 1993]. El Niño events also disrupt the marine ecology of the tropical Pacific and the Pacific coast regions of the Americas, affecting the mortality and distribution of commercially valuable fish stocks and other marine organisms [Barber and Chavez, 1983; Dessier and Donguy, 1987; Pearcy and Schoener, 1987; Lehodey et al., 1997]. Thus, though originating in the tropical Pacific, ENSO has socioeconomic consequences that are felt worldwide.
The widespread and systematic influence of ENSO on the ocean-atmosphere system, and the potential that it might be predictable seasons to years in advance, led to initiation of the international Tropical Ocean-Global Atmosphere (TOGA) Program, a 10-year study (1985–1994) of seasonal-to-interannual (also referred to as short-term) climate variability. The goals of the TOGA program were [World Climate Research Program, 1985, p. vii].
[1.] to gain a description of the tropical oceans and the global atmosphere as a time dependent system, in order to determine the extent to which this system is predictable on time scales of months to years, and to understand the mechanisms and processes underlying that predictability;
[2.] to study the feasibility of modeling the coupled ocean-atmosphere system for the purpose of predicting its variability on timescales of months to years; and
[3.] to provide the scientific background for designing an observing and data transmission system for operational prediction if this capability is demonstrated by the coupled ocean-atmosphere system.
The scientific background and rationale for TOGA was spelled out in several planning documents [e.g., World Climate Research Program, 1985; National Research Council, 1983, 1986]. Prior to TOGA, a basic description of oceanic and atmospheric variability associated with El Niño existed [e.g., Rasmusson and Carpenter, 1982], as did a basic description of tropical/extratropical atmospheric teleconnections in the northern hemisphere [e.g., Horel and Wallace, 1981]. Atmospheric general circulation models had shown a sensitivity both in the tropics and at higher latitudes to underlying equatorial Pacific SST anomalies, and theories were emerging on how tropical forcing gave rise to observed teleconnection patterns [e.g., Hoskins and Karoly, 1981]. Relatively simple wind-forced ocean models prior to TOGA were capable of simulating some aspects of seasonal-to-interannual variability associated with sea level variations in the Pacific [e.g., Busalacchi and O'Brien, 1980; Busalacchi and O'Brien, 1981; Busalacchi et al., 1983]. Initial attempts to quantitatively assess the role of ocean dynamics in controlling interannual variations in SST were underway [Gill, 1983]. Also, ocean general circulation models with explicit mixed layer thermodynamics were being developed for improved simulations of SST variability [e.g., Schopf and Cane, 1983]. Coupled tropical ocean-atmosphere models were in their infancy prior to TOGA. They showed promise though in their ability to elucidate possible mechanisms responsible for ocean-atmosphere feedbacks and in their ability to crudely simulate aspects of the ENSO cycle [McCreary, 1983; Philander et al., 1984].
Theories regarding the mechanisms responsible for El Niño variations in the ocean were likewise developing [e.g., Wyrtki, 1975; McCreary, 1976; Hurlburt et al., 1976]. The roles of ocean dynamics and, in particular, wind-forced equatorial Kelvin and Rossby waves in affecting large-scale redistribution of mass and heat in the equatorial band were widely regarded as crucial aspects of the ocean's role in the ENSO cycle. The rapid response of the equatorial ocean to wind forcing and the ability of equatorial waves to affect remote parts of the basin on relatively short timescales distinguish the tropics from higher latitudes where planetary scale waves propagate much more slowly. Substantial responses in equatorial currents and sea surface heights to relatively short-duration wind events were evident in observations before the start of TOGA [Knox and Halpern, 1982; Eriksen et al., 1983]. These observations suggested the potential for remotely forced changes in SST due to wave-induced changes in horizontal and vertical advection and upper ocean mixing. Thus understanding the oceanic processes giving rise to SST variability in the tropical Pacific was a more challenging problem than at midlatitudes, where SST variations on seasonal and interannual timescales are generated primarily by local air-sea heat exchange [Gill and Niiler, 1973].
Much of the progress in oceanographic studies related to El Niño in the 1970s and early 1980s was stimulated by fieldwork and modeling efforts as part of the Equatorial Pacific Ocean Climate Studies (EPOCS) program [Hayes et al., 1986], the North Pacific Experiment (NORPAX) [Wyrtki et al., 1981], and the Pacific Equatorial Ocean Dynamics (PEQUOD) experiment [Eriksen, 1987]. These programs provided new data for basic description of phenomenology, for developing and testing dynamical hypotheses, and for model development and validation [Halpern, 1996]. Impressive though the scientific advances were during this period, they were still inadequate in many respects. To quote from the document U.S. Participation in the TOGA Program [National Research Council, 1986, p. 6–7]:
[1.] The subsurface signature of El Niño events and the time-dependent fluxes of momentum and energy at the air-sea interface are known only qualitatively, and existing observations are inadequate to define them with the accuracy needed for initializing and verifying models.
[2.] Major uncertainties still exist concerning the tropical and southern hemisphere atmospheric circulations and their interannual variability.
[3.] The processes that determine the sea surface temperature distribution and the surface wind field over the tropics are not yet well understood.
[4.] The fundamental behavior and predictability of the coupled climate system are just beginning to be understood.
TOGA, initiated by the World Climate Research Program [1985], provided a framework for coordinated, sustained international efforts aimed at addressing these shortcomings. Implementation of TOGA was to be carried out with major new initiatives in modeling, process-oriented field studies, and long-term observations. Efforts in these areas were to be highly interactive and mutually reinforcing. Models and the results of process studies would be used to help guide the development of long-term observational systems. Long-term observations in turn would provide a large-scale, long-term framework in which to interpret the results of shorter-duration, geographically focused, intensive process studies. Long-term observations would also be used to validate models, to aid in the development of parameterization schemes for subgrid scale model physics, and to initialize dynamical model-based climate forecasting schemes.
The need for an improved observing system was underscored during the planning stages of TOGA in the early 1980s, when the scientific community was caught completely off guard by the 1982–1983 El Niño, the strongest in over a hundred years (see Appendix A for details). This El Niño was neither predicted nor even detected until several months after it had started. The lesson from this experience was obvious: an in situ observing system capable of delivering data in real time was urgently needed for improved monitoring, understanding, and prediction of El Niño and related phenomena. To meet these requirements, the TOGA Implementation Plan called for the development of a "thin monitoring" array of in situ measurements based on the enhancement of existing capabilities [International TOGA Project Office, 1992]. This observing system was to provide data on a basin scale for at least 10 years without significant temporal gaps, so that a continuous record of climate variability could be assembled. Ten years was considered the minimum length of time needed for a comprehensive study of interannual variability, the dominant mode of which was ENSO cycle.
The purpose of this paper is to describe the development of the TOGA observing system, to highlight scientific advances that have resulted from implementation of this system, and to summarize how data from this system have contributed to progress in developing models for improved climate analysis and prediction. We will emphasize oceanic, rather than atmospheric, components of the observing system, reflecting relative levels of effort expended on implementation during the TOGA decade. However, we will discuss TOGA efforts to augment the World Weather Watch for atmospheric measurements and to establish a specialized network of island-based wind profilers.
We will also emphasize in situ rather than satellite data. Satellite missions were generally initiated for purposes other than, or only partially motivated by, short-term climate research (e.g., operational weather prediction, national defense, general oceanographic and/or meteorological applications). Also, delays in satellite missions and/or temporal discontinuities in satellite data coverage heightened reliance on in situ measurements during the TOGA decade. For example, launch of the National Aeronautics and Space Administration's scatterometer (NSCAT) for surface wind velocity estimates, originally scheduled for 1989, was repeatedly delayed until August 1996, almost 2 years after the end of TOGA. The satellite carrying NSCAT then failed prematurely, in June 1997, after being operational for only 8 months. Similarly, there was a 2-year hiatus in satellite sea level altimetry measurements between the end of the U.S. Navy's Geodetic Satellite (Geosat) mission in 1989 and the launch of European Space Agency's European Remote Sensing Satellite (ERS-1) in 1991. Nonetheless, we will discuss those satellite missions that contributed directly to TOGA objectives, particularly with regard to oceanic variability. Satellite measurements targeted more toward documenting and understanding atmospheric variability during TOGA, namely those for precipitation, water vapor, clouds, radiation, and evaporation [Lau and Busalacchi, 1993], are discussed in work by Wallace et al. [this issue].
Originally, it was anticipated that TOGA would develop a balanced research agenda with significant levels of effort directed at variations in all three tropical oceans [World Climate Research Program, 1985]. Important dynamical linkages between ENSO and climate variability in the other tropical ocean basins were evident [e.g., Barnett, 1983; Horel et al., 1986]. In addition, phenomena significantly impacting regional climate, such as the Indian monsoon [Webster et al., this issue], the Indian Ocean dipole [Nicholls, 1989], El Niño-like warm episodes in the equatorial Atlantic [Philander, 1986], and the so-called "Atlantic SST dipole" [Moura and Shukla, 1981], were not well understood in terms of underlying physical processes or potential predictability. However, the strength of the ENSO signal and its global impacts, coupled with limited financial resources, tended to concentrate most efforts in the Pacific. This review therefore focuses primarily on the Pacific. Recognizing that some elements of the observing system (satellite and in situ) are more global in character, this broader geographic coverage will be noted as appropriate.
Before concluding this introduction, we note that there is a range of interpretations in the literature on use of the terms El Niño, La Niña, and ENSO [Scientific Committee on Ocean Research (SCOR), 1983; Deser and Wallace, 1987; Enfield, 1989; Aceituno, 1992; Glantz, 1994; Trenberth, 1997]. Originally, the term El Niño (in reference to the Christ child) denoted a warm southward flowing ocean current that occurred every year around Christmas time off the west coast of Peru and Ecuador. The term was later restricted to unusually strong warmings that disrupted local fish and bird populations every few years. However, as a result of the frequent association of South American coastal temperature anomalies with interannual basin-scale equatorial warm events, El Niño has also become synonymous with larger-scale, climatically significant, warm events. There is not, however, unanimity in the use of the term El Niño. In this paper, therefore, we will adopt a standard of referring interchangeably to El Niño, ENSO warm event, or the warm phase of ENSO as those times of warm eastern and central equatorial Pacific SST anomalies. Conversely, the terms La Niña, ENSO cold event, or cold phase of ENSO will be used interchangeably to describe those times of cold eastern and central equatorial Pacific SST anomalies. As noted earlier, the terms ENSO and ENSO cycle will be used to describe the full range of variability observed in the Southern Oscillation Index, including both warm and cold events.
The rest of the paper is organized as follows. We begin in section 2 with a brief overview of El Niño as the primary phenomenological target of the TOGA observing system and then describe the observing system design in terms of primary variables measured and platforms used for implementation. Scientific progress through descriptive and diagnostic studies is reviewed in section 3. Section 4 describes how the TOGA observing system contributed to the development of dynamical models for seasonal-to-interannual climate analysis and prediction. The paper concludes in section 5 with a summary and a brief discussion of future directions for climate observations based on the successes of TOGA. Four appendices are included, the first of which (Appendix A) describes the failure to observe the onset of the 1982–1983 El Niño. Appendices B, C, and D provide historical background and technical information related to development of the in situ oceanographic components, the ocean-related satellite components, and the in situ meteorological components, respectively, of the observing system. A partial list of current World Wide Web sites for access to data and data analysis products engendered by the TOGA observing system can be found in the National Research Council's [1996] report on TOGA. In addition, reports on the TOGA observing system at various stages in its development can be found in work by McPhaden and Taft [1984], U.S. TOGA Office [1988], Nova University [1989], World Climate Research Program [1990b], and the National Research Council [1990].
We begin with a brief overview of El Niño, which was the primary phenomenological focus of TOGA, in order to highlight physical principles that helped to guide development of the TOGA observing system. This overview parallels what was known at the start of TOGA with the caveat that, as a conceptual model, many of its key mechanisms were poorly understood or not yet critically tested from observations. Progress beyond this simple description is taken up in sections 3 and 4.
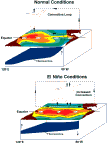
In the tropical Pacific, net heat gain from the atmosphere tends to create a warmer surface layer near the equator than at higher latitudes. Under normal conditions (Figure 1, top), easterly trade wind forcing drives near-equatorial surface flow westward in the South Equatorial Current (SEC), piling up this warm surface layer in the western Pacific to create a deep warm pool. Conversely, warm water is drained from the eastern Pacific, leading to an upward tilt of the thermocline to the east. The relative shallowness of the thermocline in the eastern Pacific increases the efficiency of local trade-wind-driven equatorial upwelling to cool the surface, creating a cold tongue in SST that extends from the coast of South America to near the international date line. The easterly trade winds are reinforced by the east-west SST contrast, which is associated with low atmospheric surface pressure over the warm pool in the west and high surface pressure over the cooler waters of the eastern Pacific. Atmospheric circulation on the equatorial plane (that is, the Walker circulation) is closed by ascent of warm moist air over the warm pool (associated with deep convection and precipitation), westerly winds aloft, and subsidence in the high-pressure zone of the eastern Pacific. In the ocean, westward flow in the surface SEC is in part compensated by a return flow to the east in the thermocline, i.e., the Equatorial Undercurrent (EUC). This current flows down the zonal pressure gradient associated with the east-west tilt of the thermocline and provides a source of water for upwelling in the east [Bryden and Brady, 1985].
Figure 1: Schematic of normal and El Niño conditions in the equatorial Pacific. See section 2 for discussion.
During El Niño (Figure 1, bottom), the trade winds weaken in the central and western Pacific, leading to a local eastward acceleration of the surface currents. In addition, weakening of the trade winds excites downwelling equatorial Kelvin waves, which propagate into the eastern equatorial Pacific, where they depress the thermocline, and upwelling equatorial Rossby waves, which propagate into the western Pacific, where they elevate the thermocline [Wyrtki, 1975; McCreary, 1976; Hurlburt et al., 1976]. Anomalously warm sea surface temperatures appear from the coast of South America to west of the international date line, and the pattern of deep convection and precipitation shifts eastward with the warmest SSTs [Gill and Rasmusson, 1983]. Deep convection is the principal driving force for atmospheric circulation through the release of latent heat at midtropospheric levels, and these shifts in the centers of deep convection during El Niño affect the atmospheric circulation on a global basis [Horel and Wallace, 1981].
The physical basis for ENSO and related phenomena provided a rationale for the development of an observing system to measure key oceanographic and meteorological variables. Prioritization of these variables was based on the need not only to better document and understand but also to predict short-term climate variability. Foremost were fields of surface wind stress and sea surface temperature since, as evident from discussion in the preceding section, it is these two variables by which the ocean and atmosphere most immediately interact in the tropics.
Of next highest priority was the upper ocean thermal field. The basic periodicity of ENSO is controlled in part by the vast thermal inertia of the upper ocean through the propagation of planetary-scale equatorial waves. These waves mediate coupling to the atmosphere on interannual timescales by redistributing upper ocean heat not only zonally along the equator, as evident in Figure 1, but also meridionally [Wyrtki, 1985a]. Thus the "memory" for the ENSO cycle is to be found in the ocean rather than in the atmosphere, where (excluding the mean seasonal cycle, which is externally forced by variations in insolation) intrinsic timescales are much shorter and are primarily associated with 3–5-day weather variability. Also, the slow evolution of upper ocean heat content on seasonal-to-interannual timescales suggested a logic for initializing ocean models used in climate prediction with subsurface temperature data.
Sea level variability was likewise deemed to be a crucial variable because it is a proxy for upper ocean heat content. The tropical oceans behave in many ways as a two-layer fluid, with thermocline variations reflected in sea level heights [Rebert et al., 1985]. For example, during ENSO, sea level is elevated when the thermocline deepens in the eastern Pacific, and it is depressed when the thermocline shoals in the western Pacific. Sea level thus provides a convenient measure of the vertically integrated oceanic response to atmospheric forcing.
Measurement of ocean currents was deemed to be essential for meeting the goals of TOGA because of the strong control ocean dynamics plays in creating ENSO SST anomalies. In most parts of the world ocean, seasonal-to-interannual changes in SST are controlled simply by variations in heat flux across the air-sea interface. In the equatorial Pacific, on the other hand, changes in three-dimensional ocean circulation play a crucial role in generating ENSO SST anomalies through horizontal advection and through changes in intensity of upwelling in the cold tongue region. To a certain extent, the need for information on the horizontal flow field could be met via estimates from the thermal field via geostrophy. However, it was also considered essential to directly measure horizontal currents along the equator, where pure geostrophy breaks down, and in the surface mixed layer, where frictional Ekman flows were expected to be large and likewise inaccessible via the geostrophic approximation.
Surface winds, SST, upper ocean thermal structure, sea level, and ocean currents, though of central importance in motivating the development of an observing system for TOGA, were of course not the only variables considered to be of value for studies of ENSO and related phenomena. It was appreciated that a quantitative understanding of SST variability required improved estimates of surface heat fluxes, that salinity variability needed to be better documented in the tropical oceans for a variety of reasons (e.g., its contribution to static stability and dynamic height, and its potential role in the surface heat balance in regions of heavy rainfall), and that studies of atmospheric circulation would benefit from an improved definition of precipitation (an integral measure of latent heat release) over the ocean. TOGA-sponsored research activities thus addressed measurement issues aimed at variables other than winds, SST, upper ocean thermal structure, sea level, and currents. However, these five key variables were viewed as a sine qua non both for improved understanding of short-term climate variability (section 3) and for the development of climate forecast models with significant predictive skill (section 4).
It was also recognized at the start of TOGA that, although ENSO is predominantly a large-scale, interannual perturbation of the climate system, it could not be effectively observed without taking into account smaller-scale, higher-frequency fluctuations. There is a broad spectrum of variability in both the ocean and the atmosphere that represents a potential source of geophysical noise in estimates of climate signals. Noise contamination can arise because of inadequate sampling in space and/or time, which will alias energy from high-frequency, small-scale fluctuations into the lower frequencies and larger scales of climatic interest. The existence of this broad spectrum of variability imposes stringent sampling requirements for climate observations. As an example, Halpern [1988a] and Mangum et al. [1992] determined that about one sample per day would be required at a given location in the equatorial Pacific to estimate monthly mean winds with an accuracy of 0.5–1.0 m s-1. Much of the equatorial Pacific was significantly undersampled relative to this criterion by volunteer observing ships (VOS), the main source of information on surface winds prior to and during the early stages of TOGA. Furthermore, some high-frequency variations were likely to be dynamically relevant in the evolution of El Niño. Potential scale interactions result from nonlinearities in the ocean-atmosphere system through processes such as atmospheric convection, ocean mixing, heat and momentum advection, etc. Considerable debate, for example, revolved around the role of episodic 1–10-day westerly wind bursts and the 30–60-day intraseasonal Madden and Julian Oscillation [Madden and Julian, 1971, 1972] in either triggering or sustaining El Niño events or in accounting for the irregular periodicity of El Niño [e.g., Keen, 1982; Luther et al., 1983; Harrison and Schopf, 1984; Lau and Chan, 1986].
Resolution and accuracy requirements established by TOGA for the measurements discussed in this study are presented in Table 1, as excerpted from the fourth edition of the "TOGA International Implementation Plan" [International TOGA Project Office, 1992]. These requirements evolved during the program as understanding of the climate system and technical capabilities improved. Table 1 represents the final assessment of the TOGA community, taking into account developments up to 1992. No specific requirements were set for subsurface temperature. For this variable it was felt that available observational techniques would fall short of expectations, especially in terms of resolution, except in certain well-sampled regions. Note that as a practical matter, surface wind velocity rather than wind stress is measured over the oceans, with stress estimated from wind velocity using bulk turbulent transfer formulae. As specified in Table 1, an accuracy of 0.01 Pa (1 Pa = 1 N m-2) for surface stress translates roughly into an accuracy requirement of 0.5 m s-1 for surface winds in regions of trade wind forcing.
Table 1. TOGA Data Requirements
The requirements in Table 1 were generally cast in terms of mapping and/or documenting variability, rather than in terms of requirements for initialization of climate forecast models. These latter requirements are still a matter of ongoing research. Nonetheless, by the standards of Table 1, it could be claimed that by the end of TOGA the observing system met many of the data requirements in the equatorial Pacific Ocean between 8°N and 8°S. This is partly because that was where most in situ resources were concentrated and partly because TOGA data requirements in some instances (e.g., subsurface temperature and sea level) were based on what was considered technically feasible. Outside the latitude band 8°N–8°S in the tropical Pacific, and in the tropical Atlantic and Indian oceans, the observing system fell short of specific requirements in Table 1.
In the following subsection we provide a brief summary of the observing system, element by element. Additional technical details such as instrumental design and instrumental accuracies are elaborated on in Appendices B, C, and D.
In situ elements of the oceanographic observing system developed and implemented in support of TOGA objectives are illustrated in and summarized in Figures 2 and 3 and summarized in Tables 2 and 3. These elements include an island and coastal tide gauge network to provide sea level measurements; drifting buoy arrays to provide mixed layer velocity and SST measurements; the TOGA Tropical Atmosphere-Ocean (TAO) array of moored buoys to provide surface wind, SST, upper ocean temperature, and current measurements; and a volunteer observing ship (VOS) expendable bathythermograph (XBT) program for upper ocean temperature profiles. The XBT program was embedded in the ongoing program of VOS surface marine meteorological measurements, which provided wind, SST, and other surface data. TOGA also inherited a decade-long VOS sea surface salinity network in 1985. In addition, repeat hydrographic sections from regularly scheduled research cruises, most notably along 110°W [McPhaden and Hayes, 1990b; Hayes et al., 1991c], 165°E [Delcroix et al., 1992], and 137°E [Shuto, 1996], provided valuable information on upper ocean water mass structures in the Pacific during TOGA.
Figure 2: The in situ Tropical Pacific Ocean Observing System developed under the auspices of the TOGA program. (top) The observing system in January 1985 at the start of TOGA; (middle) the observing system in July 1990 at the time of the TOGA midlife conference in Honolulu [World Climate Research Program, 1990b]; (bottom) the observing system in December 1994 at the end of TOGA. The four major elements of this observing system are (1) a volunteer observing ship expendable bathythermograph program (shown by schematic ship tracks); (2) an island and coastal tide gauge network (circles); (3) a drifting buoy program (shown schematically by curved arrows); and (4) a moored buoy program consisting of wind and thermistor chain moorings (shown by diamonds) and current meter moorings (shown by squares). Thick ship tracks indicate expendable bathythermograph sampling with 11 or more transects per year; thin ship tracks indicate sampling with 6–10 transects per year. Although emphasis is on 30°N–30°S, termini of VOS XBT lines originating outside these limits are nonetheless shown. One drifting buoy schematic represents 10 actual drifters. Only those tide gauge stations are shown that reported their data to the TOGA Sea Level Center in Honolulu within 2 years of collection. Some tide gauge stations are so close as to be overplotted on one another. By December 1994 most measurements made as part of this four-element observing system were being reported in real time, with data relay via either geostationary or polar orbiting satellites.
Figure 3: The in situ TOGA Ocean Observing System in its final configuration in December 1994. (top) Pacific Ocean, (bottom) Indian and Atlantic Oceans. Symbols are as in Figure 2.
Table 2. In Situ Elements of the TOGA Ocean Observing System
Table 3. Growth of Various In Situ Observing Arrays
A key feature of the array elements shown in Figures 2 and 3 was that by the end of TOGA most of the data were transmitted to shore via satellite relay in real time. In addition, each array element had unique measurement capabilities that were advantageous for TOGA (Table 2). However, none of these elements by themselves would have been adequate for TOGA purposes, because each has certain disadvantages in terms of cost and/or sampling characteristics that limit its applicability for short-term climate studies. These array components were therefore viewed as complementary to one another, providing a synergistic framework in which to document and analyze climate fluctuations in the tropical oceans.
Design of the observing system was guided by general circulation model simulations of wind-forced oceanic variability and by empirical studies of space-time correlation scales. Model design studies indicated, for example, that basin-scale wind measurements were required within at least ~7° of the equator to simulate accurately the seasonal-to-interannual evolution of SST variability in the cold tongue region of the equatorial Pacific, and that the ocean responds most sensitively to zonal wind rather than meridional wind forcing on these timescales [Harrison, 1989]. Empirical studies indicated that zonal wind field variations are minimally coherent over 2°–3° latitude and 10°–15° longitude [Harrison and Luther, 1990], and that approximately one sample per day would be required to meet TOGA accuracy requirements [Halpern, 1988a; Mangum et al., 1992]. The space scales and timescales of upper ocean thermal structure are depth dependent and nonstationary in time. However, the most stringent thermal field sampling requirements (for thermocline temperature during non-ENSO periods) are comparable to those for zonal winds [e.g., Meyers et al., 1991; Hayes and McPhaden, 1992; Kessler et al., 1996]. Scales of variability and sampling requirements for velocity were described in work by Hansen and Herman [1989], World Climate Research Program [1990b], and McPhaden et al. [1991].
Design of the observing system was constrained by logistical considerations, such as the availability of islands suitable for tide gauge installation and the availability of commercial shipping routes. It was also constrained by the practicalities of cost, since financial resources were limited. Implementation was based on existing technologies, although measurement capabilities and cost efficiencies were greatly enhanced by two significant technological breakthroughs. One was the development of a low-cost Autonomous Temperature Line Acquisition System (ATLAS) wind and thermistor chain mooring capable of telemetering its data in real time [Hayes et al., 1991a]. The second was the development of a low-cost, long-lived drifting buoy with accurate water-following characteristics [Niiler et al., 1995].
The in situ observing system was much better developed in the Pacific than in the Atlantic and Indian Oceans, as evident in Figure 3 and Table 3. In the Atlantic and Indian Oceans, fewer VOS XBT tracks and tide gauge stations were instrumented, and no long-term moorings were deployed for TOGA purposes. Drifter deployments were occasionally made in the tropical Atlantic and Indian Oceans during TOGA [e.g., Integrated Global Ocean Services System (IGOSS), 1992], but there was no program of sustained drifter deployments undertaken in either basin specifically by TOGA investigators until near the end of the program.
The full TAO array of ~70 moorings is situated between 8°N and 8°S, 95°W and 137°E and spans over one third the circumference of the globe at the equator (Figure 2). The backbone of the array is the low-cost ATLAS wind and thermistor chain mooring [Hayes et al., 1991a]. Five long-term current meter mooring sites are also maintained along the equator [World Climate Research Program, 1990a]. The array was built up primarily during the second half of TOGA (Figure 2 and Table 3) and was completed only at the very end of TOGA in December 1994 [McPhaden, 1995]. A major advantage of the TAO array was its finely resolved (daily or higher temporal resolution) time series data of key variables, particularly winds, which significantly reduced the amount of aliased high-frequency energy in the climate signals of interest. Data were transmitted in real time to shore via Service Argos then retransmitted on the Global Telecommunications System (GTS). Financial support was derived mainly from the United States, France, Japan, Taiwan, and Korea.
A TOGA/World Ocean Circulation Experiment (WOCE) Surface Velocity Program (SVP) was organized at the beginning of TOGA to seek broad international support for drifter acquisitions and deployments. At the time, there were several competing designs of unknown water-following characteristics. Several years of engineering and design work led to the Global Lagrangian Drifter with a mean lifetime (defined in terms of drogue retention) of roughly 300–400 days. Position information, SST, and other drifter data were telemetered to shore in real time via Service Argos then retransmitted on the GTS. In TOGA, drifters were deployed from research vessels, VOS, and airplanes. The objective was to maintain drifter arrays with enough samples in 2° latitude × 8° longitude areas to define the mean 15-m circulation, the seasonal cycle [Reverdin et al., 1994], and ENSO-related anomalies [Frankignoul et al., 1996]. SST data from the drifters have also proven to be critical for operational SST analyses (see Appendix C). By the end of TOGA, over 700 drifters were operational in the global oceans, over one third of which were deployed in the tropical Pacific. The SVP emerged from TOGA as the Global Drifter Program, maintained with resources from 16 countries.
TOGA inherited a substantial Pacific tide gauge network that was largely installed during NORPAX. Though design of the tide gauge network was constrained by the availability of islands where gauges could be placed (Figures 2 and 3), efforts in the Pacific during TOGA were focused on expanding and refining this network, under the direction of the University of Hawaii Sea Level Center. By the end of TOGA the number of stations in the Pacific had more than doubled (Table 3). Relative growth was equally impressive in the Atlantic and Indian Oceans, although the number of sites instrumented in those oceans was fewer than in the Pacific. Many sites were linked to the Hawaii Center via data channels on geostationary satellites. In addition, many of the TOGA tide gauges contributed to the Integrated Global Ocean Services System (IGOSS) Sea Level Project in the Pacific, for which data were made available via GTS with a delay of 1 month.
There are currently around 7000 VOS worldwide, operated by about 50 countries. They collect observations on sea surface pressure, wind velocity, sea state, humidity, and SST as part of the World Weather Watch (WWW). On a few routes, surface salinity is also sampled. Each month, typically 100,000 or more surface observations are collected and transmitted in real time to national meteorological centers via satellite communication systems or via coastal radio stations, then entered onto the GTS for general use. Prior to the establishment of TAO and other dedicated TOGA observing systems, data from VOS marine reports and from island weather stations constituted the bulk of the available information on seasonal and interannual variability in tropical surface marine meteorological fields. Important data sets and products such as the Florida State University (FSU) wind analysis [Stricherz et al., 1992] and Comprehensive Ocean-Atmosphere Data Set (COADS) [Woodruff et al., 1987] derive largely from VOS surface marine observations.
A subset of VOS ships also collect XBT data, and ~150,000 temperature profiles to a depth of 400 m or more were added to the climatological database during TOGA in the tropical Pacific. Design of the VOS XBT array for TOGA was based on a strategy of low-density sampling to provide broad-scale, widely dispersed coverage in areas of routine merchant shipping on a monthly-to-quarterly cycle for description of large-scale thermal field signals. Recommended low-density XBT sampling was prescribed as one XBT drop per 1.5° latitude by 7.5° longitude per month. TOGA also recognized a need to observe seasonal and interannual variations of major geostrophic currents in the tropical oceans. A strategy of frequently repeated sampling with higher along-track resolution was devised for a few transequatorial VOS lines to meet this need [Meyers et al., 1991]. On some routes, expendable conductivity-temperature-depth (XCTD) data were also collected [Roemmich et al., 1994]. By the end of TOGA most VOS XBT data were telemetered to shore in real time via Service Argos or via geostationary satellites, then retransmitted on the GTS.
Complementing in situ oceanographic observations were satellite missions to measure SST, sea level, and winds (Table 4). Sea level measurements were provided from altimeters flown on the Geosat mission, the ERS-1 mission, and the joint National Aeronautics and Space Administration (NASA)/Centre National d'Études Spatiales (CNES) TOPEX/POSEIDON mission. SST measurements were derived principally from multichannel advanced very high resolution radiometers (AVHRR) carried aboard the National Oceanic and Atmospheric Administration (NOAA) series of polar orbiting weather satellites. Wind speeds were measured by the special sensor microwave imager (SSM/I) deployed on the Defense Meteorological Satellite Program (DMSP) sponsored by the U.S. Department of Defense. Remotely sensed wind velocities were first available during TOGA beginning in 1991 from a scatterometer aboard the ERS-1 satellite. Note that Table 4 does not list all the wind speed and SST data available during TOGA from satellite platforms. For example, SST information was available from the along-track scanning radiometer on ERS-1, and wind speed was available from altimeter missions. The emphasis in Table 4 is on those satellite data sets which for technical reasons were most widely applied in TOGA studies.
Table 4. Key Satellite Contributions to the TOGA Ocean Observing System
Satellite measurements have the advantage of being global, or nearly so, in coverage and quasi-synoptic in time, and they often have better spatial and/or temporal resolution than in situ data. The increased use of satellite data did not diminish the need for in situ oceanographic measurements, however. In situ techniques are required for measurements of variability below the surface of the ocean. Also, satellite systems rely on complicated algorithms to convert measurements of electromagnetic radiation into geophysically meaningful variables. To be useful, satellite data must be calibrated and validated against in situ observations in order to detect and remove potential biases induced by orbital errors, instrumental errors, and/or atmospheric effects (e.g., water vapor, clouds, and aerosols).
Considerable effort was devoted to calibration and validation during TOGA for satellite-derived estimates of SST [e.g., Liu, 1988; Allen et al., 1995], SSM/I surface wind speed [e.g., Bates, 1991; Halpern, 1993; Boutin and Etcheto, 1996], surface wind velocity from the ERS-1 scatterometer [Bentamy et al., 1996; Rufenach, 1995], sea level from Geosat and TOPEX/POSEIDON [Cheney et al., 1989, 1994; Busalacchi et al., 1994; Delcroix et al., 1991, 1994; Katz et al., 1995a; Picaut et al., 1995], and surface zonal geostrophic currents derived from satellite altimetry [Picaut et al., 1990; Menkes et al., 1995]. The accuracies achieved depended on the particular satellite sensor and the level of data processing (Appendix C). Also, blended satellite/in situ products were developed during TOGA to take advantage of the strengths of both types of data. These products include the SSM/I-based wind analysis merged with in situ data and European Center for Medium-Range Weather Forecasts (ECMWF) model output [Atlas et al., 1991, 1996] and the National Centers for Environmental Prediction (NCEP) blended satellite/in situ SST analysis, an example of which is shown in Figure 4 for the last week of TOGA [Reynolds and Smith, 1994, 1995] (see also Appendix C, section C1).
Figure 4: (top) SST weekly mean and (bottom) anomaly for December 25–31, 1994. The contour interval is 1°C, except there are two extra contours at ±0.5°C in Figure 4 (bottom). Negative contours are dashed. Heavy contour lines are used every 5°C in Figure 4 (top) and every 2°C in Figure 4 (bottom). In Figure 4 (top) the heavy shading at values < –1.75°C approximates the sea ice coverage. The anomalies are computed as departures from the monthly climatology of Reynolds and Smith [1995], which was interpolated to the weekly time period.
Most long atmospheric time series available for climate research derive from the operational activities of the WWW. At the start of TOGA, there were about 400 upper air reporting stations between 30°N and 30°S as part of the WWW, of which TOGA identified 150 as a minimal network for documenting planetary-scale variations in atmospheric circulation. Thus the basic elements of an upper air observing system existed at the outset of TOGA. Even so, this WWW network of stations was not adequate for TOGA purposes. As a consequence, initial planning for TOGA by the various scientific bodies noted the strong desirability of expanding the network of WWW rawinsonde sites in the tropics, especially in the Pacific and Indian Ocean sectors. Sites eventually instrumented under TOGA auspices included Tarawa, Kanton, Penrhyn, and San Cristóbal (in the Galápagos Islands) in the Pacific (Figure 5) and the island of Gan in the Indian Ocean. Unfortunately, the WWW network in the tropics in general underwent significant declines in data collection and exchange through the GTS during the TOGA decade for a variety of technological, political, and economic reasons [National Research Council, 1994a].
Figure 5: Map of the tropical Pacific Ocean basin
showing the locations of wind profilers and conventional upper air sounding
systems used for enhanced atmospheric observations during TOGA. Shown are VHF
and UHF profiler sites at Biak (Indonesia) and Christmas Island (Kiribati);
stand-alone VHF sites at Pohnpei (Federated States of Micronesia) and Piura
(Peru); stand-alone UHF profiler sites at Tarawa (Kiribati) and San Cristobal
(Galapagos Islands); and integrated sounding systems (ISS) at Manus Island (Papua
New Guinea), Kapingamarangi (Kiribati), and the island Republic of Nauru. The
ISS system consists of a UHF profiler integrated with a balloon sounding system
and surface meteorological instruments; the ISS sites at Manus Island, Nauru,
and Kapingamarangi were established as part of TOGA COARE. World Weather Watch
sites using conventional sounding systems were maintained at Tarawa, Kanton
(Kiribati), San Cristobal, and Penrhyn. Not shown is the World Weather Watch
(WWW) upper air sounding station site established by TOGA at Gan (0.5°16.1 S,
73°16.1
S,
73°16.1 E) in the Maldive Islands.
E) in the Maldive Islands.
TOGA also supported the establishment of wind profilers at several sites throughout the Pacific Basin (Figure 5), beginning with the 50-MHz very high frequency (VHF) wind profiler that commenced operation at Christmas Island in April 1986 [Gage et al., 1990, 1991a]. This Transpacific Profiler Network provides measurements of tropospheric winds between altitudes of 1.8 and 18 km height. Four times per day, hourly averaged VHF profiler data are telemetered via geostationary satellite and incorporated into the GTS for worldwide distribution. In addition, 915-MHz ultrahigh frequency (UHF) wind profilers were installed at Biak, Indonesia; Tarawa, Kiribati; and San Cristóbal, in the Galápagos Islands of Ecuador to provide more information on boundary layer wind variability.
The long-term mean and mean seasonal cycle are crucial for understanding interannual variations in the coupled system. Background stratification, for example, affects the length scales, timescales, and phase speeds of planetary equatorial waves thought to be important in the ENSO cycle. Likewise, zonal asymmetries in the background state of the equatorial ocean due to mean trade wind forcing, e.g., the mean zonal slope of the equatorial thermocline and zonal SST gradient associated with it (shown schematically in Figure 1), establish conditions necessary for the growth of ENSO-related SST anomalies [e.g., Battisti and Hirst, 1989]. El Niño anomalies also tend to be phase locked to the seasonal cycle, with warmest El Niño SST anomalies often occurring in boreal winter in the equatorial cold tongue, when SST is seasonally at its coldest [Rasmusson and Carpenter, 1982]. Empirical and modeling studies have indicated that persistence and predictability of ENSO anomalies is seasonally modulated, being highest in boreal summer and winter and falling off through the boreal spring [Latif and Graham, 1992; Webster and Yang, 1992; Latif et al., 1994; Balmaseda et al., 1995]. Some theories also suggest that the mean seasonal cycle determines the basic periodicity and irregularity of the ENSO cycle via chaotic nonlinear self-interaction [e.g., Jin et al., 1994; Tziperman et al., 1994; Chang et al., 1995]. However, few, if any, coupled ocean general circulation models (GCMs) are capable of simulating both the mean seasonal cycle and interannual ENSO-like variability with equal degrees of veracity [Mechoso et al., 1995]. Finally, seasonal variations for some variables (e.g., SST in the eastern Pacific) are as large as, or larger than, ENSO-related interannual anomalies. Therefore, at minimum, one requires a clear definition of the climatological mean seasonal cycle for model validation and in order to accurately define interannual climate anomalies. Climatologies existed prior to TOGA, but in some cases, especially for subsurface oceanographic variables, they were of poor quality because of the sparsity of data on which they were based.
Key features important in characterizing the coupled ocean-atmosphere system in the equatorial Pacific include the western Pacific warm pool with SSTs > 28°C and the equatorial cold tongue of the eastern and central equatorial Pacific (Figure 4). These structures, evident in all long-term mean SST climatologies, are modulated in intensity and areal coverage on seasonal, interannual, and decadal timescales. Understanding how these features relate to surface winds and subsurface ocean hydrodynamics is critical to understanding climate variability related to ENSO.
An example of the improved definition from the TOGA observing system of mean upper ocean temperature, surface dynamic height, and wind stress along the equator is shown in Figure 6. The mean temperature section, on the basis of all available TAO data between 2°N and 2°S, is similar to that presented by Kessler et al. [1996]. It shows the increase in SST from east to west, the warm pool of 28°C water in the upper 100 m of the western Pacific, the downward sloping thermocline in the upper 300 m, and the existence of a weakly stratified "thermostad" of 13°C water in the eastern Pacific [Stroup, 1969]. Situated in the middle of the highly stratified upper thermocline is the 20°C isotherm; for this reason this isotherm is often used as an index for the depth of the thermocline in the tropical Pacific. The mean surface dynamic height associated with the temperature field rises by 40 dynamic centimeters (dyn. cm) between 95°W and 170°E, after which it decreases slightly to the west. Zonal variations in dynamic height and thermocline depth along the equator are a response to steady easterly trade wind forcing in the eastern and central Pacific [McPhaden and Taft, 1988]; reversal of these gradients in the western Pacific is associated with local westerly winds [see also Wyrtki, 1984; Mangum et al., 1990; McPhaden et al., 1990a]. The zonal section in Figure 6 has many features in common with sections composited from different individual cruises prior to TOGA [e.g., Philander, 1973; Halpern, 1980] but is more representative of long-term mean conditions.
Figure 6: Zonal section of mean temperature averaged between 2°N and 2°S on the basis of available TAO time series data in 1980–1996. Also shown is the corresponding mean zonal wind stress (computed using a constant drag coefficient of 1.2 × 10-3) and dynamic height 0–500 dbar (computed using mean temperature/salinity relationships based on work by Levitus and Boyer [1994] and Levitus et al. [1994a]). Crosses indicate depths and longitudes where temperature data were available. An average at a particular location was computed only if a minimum of 2 years of data was available.
The mean thermal structure of the Pacific along quasi-meridionally oriented VOS XBT lines (Figure 7) also shows the downward slope of the thermocline toward the west in response to mean trade wind forcing. In addition, the meridional structure of ridges and troughs in the thermocline, which are related to major zonal currents [e.g., Donguy and Meyers, 1996a], is also clearly delineated. Evidence of trade-wind-driven equatorial upwelling (local minima in temperatures near the equator in the surface layer) is apparent in the central and eastern Pacific sections.
Figure 7: Mean temperature for the period 1985–1994 on four well-sampled XBT lines. Typically, 120 or more realizations of the quasi-synoptic temperature field were obtained during the decade for each section. The standard deviation of seasonal-to-interannual temperature variability during 1985–1994 from the Australian ocean thermal analysis system [Smith, 1995b] is indicated by shading. Westernmost section is at the top, easternmost at the bottom.
Methods to estimate the volume transport of the major equatorial currents from monthly, synoptic VOS XBT sections, as in Figure 7, were developed by Kessler and Taft [1987], Taft and Kessler [1991], Picaut and Tournier [1991], and Donguy and Meyers [1996a]. A comparison of transports from VOS XBT data to research vessel data (Table 5) shows that all of the geostrophic current transports can be reasonably well monitored by the VOS program. Differences between means based on research vessel and VOS data are of the order of only 7–20% (Tables 5a and 5b). The temporal variation inferred from research cruise data is highly correlated to the VOS estimates [Picaut and Tournier, 1991]. Although somewhat different methods were used to calculate XBT transports by Kessler and Taft [1987] and Picaut and Tournier [1991], the mean and standard deviation of transports over a 7-year period are only slightly different (Table 5c).
Table 5a. Mean Current Transports During the Hawaii-Tahiti Shuttle From March 1979 to June 1980
Table 5b. Mean Current Transports During the Line Islands Profiling Projects (LIPP) From March 1982 to June 1983
Table 5c. Mean Current Transports From January 1979 to June 1985
Drifter data allow for a definition of the surface circulation (combined Ekman and geostrophic components) across the entire basin, rather than just along prevailing shipping routes. The average velocity at 15-m depth from the drifter data for 1988–1994 (Figure 8) shows the persistent and well-documented surface current systems of the tropical Pacific: the North Equatorial Current (NEC), South Equatorial Current (SEC), North Equatorial Countercurrent (NECC), and a vestigial South Equatorial Countercurrent (SECC) (in the region 6°–10°S, 160°–176°E). The standard error of the velocity shows that the general circulation of the tropical Pacific is well defined everywhere, even to the extent that divergence and relative vorticity fields can be computed from this data with a high degree of confidence.
Figure 8: Mean surface layer (15 m) circulation in the tropical Pacific based on Surface Velocity Program drifter data for the period 1988–1994. The ellipse at the end of each vector is the 95% confidence interval.
Significant departures from the patterns that have been reported by ship drift charts, or from interpretation of the gradients of dynamic height as an index of the surface current, emerge from the drifter data. For example, dynamic height maps show that there should be a geostrophic flow toward the equator nearly everywhere, while drifter data indicate that there is a flow toward the pole nearly everywhere. Thus the meridional Ekman flows are strong enough not only to cancel the near-surface geostrophic currents but also to transport surface layer water in the opposite direction. Surface layer Ekman divergence near the equator in particular is important in determining the equatorial upwelling circulation [Wyrtki, 1981]. Also, compared to ship drift charts, the drifter data show a splitting and divergence of the South Equatorial Current between 110° and 136°W, with maxima in westward flow to the north and south of the equator.
The seasonal cycle of SST in the equatorial Pacific has been well documented from COADS and other VOS-based analyses [e.g., Reynolds and Smith, 1995]. Warmest SSTs in the cold tongue occur in boreal spring, and coolest SSTs occur in boreal autumn. The amplitude of these annual period variations diminishes from east to west as the thermocline deepens (Figure 9); similarly, the timing of maximum temperatures occurs later in the boreal spring progressing from west to east [e.g., Horel, 1981; Enfield, 1986; Chao and Philander, 1991]. The westward progression of the annual cycle of SST along the equator in the Pacific is related to the westward progression in the zonal winds [Chang, 1994; Xie, 1994]. Annual variations in SST in turn set up atmospheric boundary layer pressure gradients which drive annual period zonal wind variations [Nigam and Chao, 1996].
Figure 9: Mean seasonal cycles of temperature and zonal velocity at four sites along the equator based on multiyear analyses (1980–1994 at 110°W, 1983–1994 at 140°W, 1988–1994 at 170°W, and 1986–1993 at 165°E). The 110°W, 140°W, and 165°E analyses are updated versions of those found in work by McPhaden and McCarty [1992] and McCarty and McPhaden [1993]. The 170°W analysis is based on data presented by Weisberg and Hayes [1995], extended through 1994.
Although solar forcing near the equator is predominantly at semiannual periods, SST in the equatorial cold tongue of the eastern and central Pacific is dominated by annual period variations because of the importance of ocean dynamics and the influence of land masses bordering the Pacific [Li and Philander, 1996]. Recent diagnostic studies and model results illustrate the complex mix of ocean processes in accounting for the amplitude and phase of seasonal SST variations in this region [Hayes et al., 1991b; Köberle and Philander, 1994; Chang, 1993, 1994; Chen et al., 1994a]. The shallow mean thermocline depth in the eastern Pacific, which is due to large-scale wind forcing (Figure 6), is important in facilitating upwelling and vertical mixing to cool the surface. Zonal advection associated with seasonally varying currents is also important, particularly in the central Pacific [Chen et al., 1994a; Minobe and Takeuchi, 1995]. Variations in surface heat fluxes (mainly solar irradiance and latent heat flux) are significant at all locations. These fluxes assume a dominant role as ocean dynamical processes diminish poleward away from the equator and in the western equatorial Pacific where the thermocline is deep. In this latter region the semiannual period in solar irradiance forcing leads to the dominant semiannual period in SST (Figure 9).
Studies using XBT and conductivity-temperature-depth (CTD) data have described the seasonal cycle of upper ocean thermal structure based on the dynamics of Ekman pumping and Rossby waves [Delcroix and Henin, 1989; Kessler, 1990; Kessler and McCreary, 1993]. Seasonal variations in transports of major currents have also been documented using XBT and tide gauge data by Taft and Kessler [1991], Picaut and Tournier [1991], and Donguy and Meyers [1996a]. Mitchum and Lukas [1990] used a set of sea level data lying along the North Equatorial Countercurrent trough to show that annual variations propagate to the west as a Rossby wave resonantly forced by westward propagating components in the wind field. Recent model simulations of the seasonal cycle, validated against TOGA observations [e.g., Minobe and Takeuchi, 1995], confirm the results of these empirical studies on the importance of wind stress forcing and equatorial wave processes.
Reverdin et al. [1994], developed a climatology of the surface currents in the tropical Pacific from TOGA drifter and mooring data. A notable aspect of the mean seasonal cycle along the equator is the "springtime reversal" of the normally westward flowing South Equatorial Current [Halpern, 1987b]. It is most evident in the eastern Pacific where, for example, eastward flow of over 30 cm s-1 occurs in April–May at 110°W (Figure 9). This reversal in flow propagates westward along the equator [McPhaden and Taft, 1988], as do zonal winds and SST [Horel, 1981; Lukas and Firing, 1985], with variations at 140° and 170°W lagging those farther to the east. The springtime reversal in the SEC had been known for nearly a century [Puls, 1895], though its magnitude was underestimated because of contamination of ship drift estimates by windage on ship's hulls [McPhaden et al., 1991]. Model simulations suggest that the springtime reversal results from the seasonal relaxation of the zonal component of trade winds, causing flow to accelerate eastward down the zonal pressure gradient [Chao and Philander, 1991; Yu et al., 1997].
The mean seasonal cycle of the Equatorial Undercurrent along the equator has been described in several reports [Halpern, 1987b; McPhaden and McCarty, 1992; McCarty and McPhaden, 1993; Weisberg and Hayes, 1995]. Juxtaposing seasonal analyses based on these studies (Figure 9) helps to highlight some of the important characteristics of variability on this timescale. The EUC, on average, is located in the upper thermocline and is therefore found at greater depths in the west than in the east. Zonal current variations are confined principally to above the Undercurrent core, with a maximum eastward flow in the thermocline occurring in boreal spring at all longitudes.
Recent analyses suggest that the seasonal cycle is nonstationary in the eastern equatorial Pacific [Gu et al., 1998]. Specifically, at 110°W the annual period in thermocline depth variations was much more pronounced in the 1990s than in the 1980s, presumably because of changes in the annual cycle of zonal wind forcing farther to the west. Interestingly, amplification of thermocline depth variations was not reflected in amplified annual SST variations at 110°W. The mean depth of the thermocline remained sufficiently shallow in the eastern Pacific that, consistent with the theories of Köberle and Philander [1994] and Xie [1994], the efficiency of ocean-atmosphere interactions and ocean dynamical processes to cool the surface would not have been significantly impacted.
Some of the hallmark manifestations of the ENSO cycle are illustrated in Plate 1, which shows time series of the Southern Oscillation Index (SOI) and of surface zonal wind stress anomalies and sea surface temperature anomalies along the equator. The period shown (1982–1995) encompasses the 1982–1983 El Niño and interannual variability during the TOGA decade (1985–1994). Each warm episode (1982–1983, 1986–1987, 1991–1992, 1993, and 1994–1995) is associated with negative SOI values and weaker than normal trade winds over about 60° of longitude in the central and western Pacific. In the case of the intense 1982–1983 El Niño the trade winds weakened progressively from west to east all the way across the basin. Conversely, the 1988–1989 cold La Niña event was associated with high SOI values and a strengthening of the trade winds over roughly 60° of longitude. Also noteworthy in Plate 1 is the persistence of warm SST anomalies near the date line and the occurrence of three distinct warm episodes in the eastern Pacific in concert with consistently low Southern Oscillation Index values between 1991 and 1995. Although it is known that the frequency and intensity of ENSO events are modulated on decadal and longer timescales [Gu and Philander, 1995], the duration of warm phase ENSO conditions over 5 calendar years is unparalleled in this century [Trenberth and Hoar, 1996].
Plate 1: Time-longitude plots of zonal pseudostress (in m2 s-2) and SST (in °C) between 2°N and 2°S along the equator from 1982–1995. Pseudostress time series are from the Florida State University (FSU) analyses [Stricherz et al., 1992], and the SST is from Reynolds and Smith [1994]. Also shown is the Southern Oscillation Index (SOI) for the same time period. The SOI, defined as the normalized difference in surface pressure between Tahiti, French Polynesia and Darwin, Australia is a measure of the strength of the trade winds, which have a component of flow from regions of high to low pressure in the tropical marine boundary layer. High SOI (large pressure difference) is associated with stronger than normal trade winds and La Niña conditions, and low SOI (smaller pressure difference) is associated with weaker than normal trade winds and El Niño conditions. All time series have been smoothed with a 5-month triangle filter (roughly equivalent to a seasonal average). The FSU pseudostress and Reynolds SST have also been smoothed zonally over 10° longitude.
The relationship between surface winds and SST for December 1994 (Figure 10) illustrates another important aspect of ENSO variability. Deep atmospheric convection typically occurs over the warmest SSTs in the tropical Pacific [e.g., Graham and Barnett, 1987]. Warmest SSTs (> 30°C) in December 1994 were situated just south of the equator near the date line in a region of strongly convergent surface winds and active deep atmospheric convection [Climate Analysis Center, 1994]. Converging winds act to sustain both deep convection (via moisture convergence) and warm SSTs (via ocean dynamics) [Philander et al., 1984]. These processes tend to locally reinforce one another, and representing them properly in coupled ocean-atmosphere models has been one of the challenges of ENSO modeling [e.g., Zebiak and Cane, 1987; Battisti, 1988; Battisti and Hirst, 1989; Schopf and Suarez, 1988].
Figure 10: Wind vectors and SSTs from the TAO array for December 1994. (top) Monthly means; (bottom) monthly anomalies from the COADS wind climatology and NCEP SST climatology (1950–1979). SSTs warmer than 29°C and colder than 27°C are shaded; SST anomalies >1°C and <-1°C are shaded.
An important oceanic feature of the ENSO cycle is the zonal redistribution of warm surface layer water masses [White et al., 1985; Donguy, 1987; Donguy et al., 1989; McPhaden et al., 1990a; McPhaden and Hayes, 1990b; Kessler and McPhaden, 1995a]. In the western Pacific the thermocline (as indicated by the depth of the 20°C isotherm) shoals 20–50 m in the latitude band 15°S to 20°N during El Niño, whereas in the eastern Pacific the thermocline deepens by a comparable amount but in a narrower band of latitudes than in the west. These thermocline depth variations, illustrated along the equator in Figure 11 for the 1991–1993 El Niño, are correlated with changes in the strength of major currents. The westward SEC weakens significantly during El Niño episodes, while in some events the NECC intensifies [Taft and Kessler, 1991; Kessler and McPhaden, 1995a]. Thus there is an anomalous eastward mass transport of warm water by the equatorial surface currents during the onset of warm events.
Figure 11: Time-longitude sections of anomalies in surface zonal winds (in m s-1), sea surface temperature (in °C), and 20°C isotherm depth (in meters) for January 1991 to December 1993. Analysis is based on 5-day averages between 2°N and 2°S of moored time series data from the TAO Array. Anomalies are relative to monthly climatologies cubic spline fitted to 5-day intervals (COADS winds, Reynolds and Smith [1995] SST, CTD/XBT 20°C depths). Shading indicates anomaly magnitudes > 2 m s-1, 1°C, and 20 m for winds, temperatures, and 20°C depths, respectively. Positive winds are westerly. Squares on the top abscissa indicate longitudes where data were available at the start of the time series, and squares on the bottom abscissa indicate where data were available at the end of the time series.
Changes in the zonal distribution of upper ocean heat content are reflected in sea level variations [e.g., Rebert et al., 1985; Delcroix and Gautier, 1987] because of the vertically coherent structure of the upper ocean thermal field on seasonal-to-interannual timescales. In other words, anomalously deep thermocline tends to be associated with anomalously high sea level and vice versa. Wyrtki [1984] described the sea surface height gradient along the equator during the 1982–1983 El Niño assuming that the long-term mean sea level at tide gauges along the equator was equal to the long-term surface dynamic height relative to a deep reference level. He showed that the normal upward slope of sea level from east to west (Figure 7) was sharply reduced and at times reversed in the eastern and central Pacific during 1982–1983. Reduction and reversal of the sea surface slope also occurred in the 19861987 and 1991–1992 El Niño events (Figure 12). Variations were weaker at these times than in 1982–1983 though, as expected from the weaker and less zonally extensive westerly wind anomalies along the equator (Plate 1). Conversely, during the 1988–1989 cold La Niña event the sea level slope along the equator intensified, in association with stronger than normal trade winds (Figure 12).
Figure 12: Zonal slope of sea surface height along the equator. Sea level anomalies from the 1975–1987 mean seasonal cycle were taken from seven locations near the equator: Rabaul (4°S, 152°E), Kapingamarangi (1°N, 155°E), Nauru (0.5°S, 167°E), Tarawa (1°N, 173°E), Kanton (3°S, 172°W), Christmas Island (2°N, 157°W), and the Galapagos Islands (0.5°S, 90°W). These anomalies were added to the mean dynamic topography difference (0–1000 dbar) computed from the Levitus and Boyer [1994] and Levitus et al. [1994a] temperature and salinity climatologies in order to calculate absolute heights. (top) Mean conditions during three warm events are shown as solid circles (June 1982 to May 1983), crosses (January to December 1987), and open circles (June 1991 to May 1992). The heavy solid line is the long-term mean conditions taken from the Levitus climatology. (bottom) Warm and cold conditions are contrasted by showing the difference (the vertical bars) of the mean sea level anomaly in 1988 (cold) minus the mean sea level anomaly in 1987 (warm).
Sea level slope along the equator is an index for the strength of the zonal pressure gradient, which is the driving force for the Equatorial Undercurrent [Philander and Pacanowski, 1980; McCreary, 1980; McPhaden, 1981]. Reduction and reversal of this sea level slope were associated with a significant weakening and disappearance of the EUC in the thermocline during the 1982–1983 El Niño [Firing et al., 1983; Halpern, 1987b] and the 1986–1987 El Niño [McPhaden et al., 1990a]. The EUC, though it did not disappear during the 1991–1993 El Niño, was greatly reduced in strength in the central Pacific for several months [Kessler and McPhaden, 1995a]. El Niño related reductions in Undercurrent strength have significant implications for the heat balance of the surface layer, since the Undercurrent is normally a source of cold water to feed equatorial upwelling [Bryden and Brady, 1985].
Near the equator, adjustment of the upper ocean heat and mass is strongly influenced by excitation and propagation of equatorial Kelvin and long Rossby waves, which are the primary mechanisms by which the winds communicate their influence to other parts of the ocean basin. The Kelvin waves most prominent in equatorial time series data are associated with forcing by westerly wind bursts and the atmospheric Madden and Julian Oscillation [Miller et al., 1988; McPhaden et al., 1988a; Kessler et al., 1995]. These waves are clearly evident in 20°C isotherm depth variations (e.g., Figure 11), as well as in time series of sea level, dynamic height, and zonal currents within 2° latitude of the equator. Using TAO data and Geosat-derived sea level data, Cheney et al. [1987], Miller et al. [1988], McPhaden et al. [1988a], McPhaden and Hayes [1990b], Delcroix et al. [1991, 1994], Johnson and McPhaden [1993a], and Picaut and Delcroix [1995] clearly documented equatorial Kelvin waves propagating eastward with first baroclinic mode phase speeds of 2–3 m s-1 prior to and during the 1986–1987 El Niño. Similarly, analysis of TAO data and TOPEX/POSEIDON sea level data indicated prominent oceanic variability due to equatorial Kelvin waves generated by wind forcing west of the date line during 1991–1995 [Busalacchi et al., 1994; Kessler et al., 1995; Boulanger and Menkes, 1995].
Weakening of the trade winds near the equator in the central and western Pacific at the onset of warm ENSO events leads to a pattern of upwelling favorable wind stress curl which elevates the thermocline locally at extraequatorial latitudes [e.g., Kessler, 1990]. Weakening of the trade winds also excites upwelling long Rossby waves [White et al., 1985, 1987; Kessler, 1990; Boulanger and Menkes, 1995; Kessler and McPhaden, 1995b], the fastest of which propagates westward at phase speeds of one third the Kelvin wave speed. The slower propagation speed of these waves compared to equatorial Kelvin waves implies that elevation of the thermocline in the west lags depression of the thermocline in the east by several months as evident in thermal field and sea level analyses (e.g., for 20°C along the equator between late 1991 to early 1992 in Figure 11). The Geosat analysis of Delcroix et al. [1991] and subsequent modeling study of du Penhoat et al. [1992] for the 1986–1987 El Niño suggest that, in addition to wind forcing, eastern boundary reflections of equatorial Kelvin waves can generate equatorial Rossby waves that affect the evolution of ENSO.
Empirical studies of the surface layer heat balance emphasize the complex mix of processes controlling SST variability on ENSO timescales. For example, the importance of remotely forced equatorial waves in mediating SST variability in the eastern and central Pacific can be inferred from Plate 1. Largest ENSO SST anomalies during 1980–1995 were located significantly to the east of the largest zonal wind anomalies; moreover, large SST anomalies were found in the far eastern Pacific where zonal wind anomalies were weak. Waves affect SST in the cold tongue region by inducing changes in thermocline depth which affect upwelling and vertical mixing rates [e.g., Hayes et al., 1991b; Kessler and McPhaden, 1995a, b]. Waves can also advect temperature fields meridionally and, more importantly, zonally along the equator. Wave- and current-induced zonal advection of the eastern edge of the warm pool produces large interannual SST anomalies in the central Pacific [McPhaden and Picaut, 1990; Picaut and Delcroix, 1995; Picaut et al., 1996].
Local air-sea heat exchanges are also important in the surface layer heat balance of the tropical Pacific on interannual time scales [Liu and Gautier, 1990; Hayes et al., 1991b; Kessler and McPhaden, 1995a]. The most strongly varying components of the surface energy balance are solar irradiance, which is modulated by changes in cloudiness, and latent heat flux which is modulated by changes in wind speed, SST, and relative humidity [Liu, 1988; Waliser et al., 1994]. East of the date line, where ocean dynamics are crucial for generating SST anomalies on interannual time scales, latent heat flux tends to increase with increasing SST, and therefore acts as a negative feedback on developing SST anomalies [Kessler and McPhaden, 1995a; Weisberg and Wang, 1997]. In the western Pacific warm pool, the thermocline is deep, mean horizontal SST gradients are weak, and ocean dynamical processes are less capable of generating large scale SST anomalies than further east. In this region air-sea turbulent heat exchange is an important generating mechanism for SST anomalies, through enhanced evaporation during periods of strong westerly winds [Meyers et al., 1986]. Variations in short wave radiation tend to damp developing SST anomalies throughout the tropical Pacific since high cloudiness, which reduces insolation, tends to occur over the warmest surface waters [Waliser et al., 1994].
Data from the TOGA observing system have been used to test various theories of El Niño and the ENSO cycle. An early theory espoused by Wyrtki [1975] suggested that prior to El Niño, the trade winds strengthened, and there was a increase in sea level (a proxy for heat content) in the western Pacific warm pool. When the trade winds weakened, the overcharged warm water pool would collapse and surge eastward in the form of a Kelvin wave to initiate a warm event. The importance of Kelvin waves in the development of El Niño has been confirmed by many studies. However, other aspects of Wyrtki's theory were undermined when prior to the 1982–1983 El Niño, the strongest of the century, there was no anomalous rise in sea level in the western Pacific or intensification of the easterly trades [Cane, 1984]. Similarly, prior to the equatorial warming in 1993, there was no buildup of heat content in the western Pacific warm pool or intensification of the easterlies [Kessler and McPhaden, 1995b].
Wyrtki [1985a] proposed another hypothesis, namely that warm water accumulated in the tropical Pacific prior to an El Niño on a zonally averaged basis between 15°N and 15°S. In this scenario, El Niño represents a mechanism whereby excess heat is purged to higher latitudes. Cane et al. [1986] interpreted the interannual oscillations in their coupled ocean-atmosphere model in terms of this mechanism. Springer et al. [1990], in a wind-forced ocean model simulation, found a buildup of heat content near the equator prior to the 1982–1983 El Niño as hypothesized by Wyrtki, but only between 5°N and 5°S. The difference in latitude bands over which the buildup was assumed to occur resulted from Wyrtki's use of tide gauge station data which had to be interpolated over great distances zonally beyond 5°N–5°S [Springer et al., 1990]. Miller and Cheney [1990], however, did not find a buildup at all prior to the 1986–1987 El Niño event using Geosat data. Thus Wyrtki's [1985a] mechanism, modified to a narrower band of longitudes, may be operative during some but not all El Niño events.
McCreary [1983] proposed a theory for ENSO in which the timescale between warm events was set by the slow westward propagation of long extraequatorial Rossby waves and their reflection off the western boundary as equatorial Kelvin waves. The reflected Kelvin waves would alter thermocline depths (and by proxy SST) in the eastern Pacific, thereby affecting the strength of the trade winds. In order to get a realistic 3–4-year periodicity for the ENSO cycle, Rossby waves with significant amplitudes at roughly 20° latitude from the equator were required. Using XBT data, Graham and White [1988] argued for the existence of extraequatorial Rossby waves along 12°N and 12°S and their reflection into equatorial Kelvin waves at the western boundary. However, Kessler [1990] offered alternative explanations for the observed variability along the equator in terms of direct wind forcing rather than Rossby wave reflection, and Kessler [1991] showed that only Rossby waves equatorward of about 8° latitude could reflect into equatorial Kelvin waves with significant amplitudes.
The delayed oscillator theory of ENSO [Battisti, 1988; Battisti and Hirst, 1989; Schopf and Suarez, 1988] also involves the reflection of Rossby waves into equatorial Kelvin waves at the western Pacific boundary. In contrast to McCreary's [1983] theory though, equatorial Rossby waves closely trapped to the equator, rather than extraequatorial Rossby waves at higher latitudes, are most relevant. Thermocline changes associated with reflected Kelvin waves lead to SST anomalies in the eastern Pacific cold tongue by altering upwelling rates. The SST anomalies affect the atmospheric convection and circulation, giving rise to local positive feedbacks that reinforce the SST and wind anomalies (e.g., Figure 10). The anomalous surface winds in turn excite equatorial oceanic waves of opposite sign to those that generated the original SST anomalies. The timescale for the ENSO cycle in this theory is set by the competition between the local positive feedbacks and delayed negative feedbacks associated with remotely forced equatorial waves and their western boundary wave reflections.
Tests of the delayed oscillator have focused primarily on the question of whether equatorial Rossby waves can reflect from the irregular and gappy coastal geometry of the western Pacific. Theories suggest coastal irregularities should not be a fundamental limitation to this reflection process [Clarke, 1991; du Penhoat and Cane, 1991]. However, although in principle western boundary reflections should work equally well to both initiate and terminate El Niño events, it appears that they are most effective in terminating events [Li and Clarke, 1994; Mantua and Battisti, 1994]. In this situation, reflection of an upwelling Rossby wave at the western boundary excites an upwelling equatorial Kelvin wave train which erodes the warm SST anomaly in the cold tongue, eventually leading to cool La Niña SST anomalies. Even so, not all warm events appear to be terminated by western boundary reflections. Boulanger and Menkes [1995], for example, found that wind-forced upwelling Kelvin waves, rather than boundary-reflected Kelvin waves, led to cooling along the equator in the eastern Pacific in late 1993. Also, Picaut and Delcroix [1995] argued that the 1986–1987 El Niño was terminated by Rossby waves emanating from the eastern boundary, rather than Kelvin waves emanating from the western boundary.
Few, if any, El Niño events of the TOGA decade appear to have been initiated by delayed oscillator physics. Through extended empirical orthogonal function (EOF) analysis of Geosat data during the 1986–1989 El Niño-La Niña cycle, White and Tai [1992] suggested that an equatorial Rossby wave reflected into an equatorial Kelvin wave at the western boundary, consistent with delayed oscillator theory. However, a detailed projection of Geosat sea level and derived surface currents on individual equatorial wave modes indicated very little evidence of first meridional Rossby wave reflection into Kelvin waves during this time [Delcroix et al., 1994]. Similarly, Kessler and McPhaden [1995b], using TAO and XBT data during 1988–1993, and Boulanger and Menkes [1995], using TAO and TOPEX/POSEIDON data during 1992–1993, found little evidence for the initiation of warm events via Rossby wave reflections at the western boundary. Boulanger and Fu [1996], using TOPEX/POSEIDON altimeter data and ERS-1 wind data, detected wind-forced downwelling equatorial Rossby waves that reflected into downwelling Kelvin waves prior to warming along the equator in middle to late 1994. They interpreted these reflections as evidence for delayed oscillator physics as a trigger for the 1994–1995 El Niño. In contrast, however, Goddard and Graham [1997] argued that this same 1994–1995 warm event in the NCEP reanalysis [Ji and Smith, 1995; see also section 4.4] was not initiated Rossby wave reflection at the western boundary, but rather direct wind forcing near the equator.
Another perspective of the ENSO cycle was proposed by Picaut and Delcroix [1995] and Picaut et al. [1996]. Using hypothetical drifters moved by current fields derived from Geosat and TOPEX/POSEIDON data, TAO mooring data and SVP drifter data, and three different classes of ocean models, these authors found that ENSO-related SST anomalies in the central western Pacific were primarily the result of zonal advection (Figure 13). Picaut and Delcroix [1995] and Picaut et al. [1997] argued that Rossby waves excited by eastern boundary reflections, in addition to the direct effects of wind forcing, were instrumental in generating these currents. Since the impacts of SST variations on the atmosphere are most pronounced in the central and western equatorial Pacific [Geisler et al., 1985], Picaut et al. [1997] argue for a revision of the delayed oscillator theory to provide more weight to oceanic processes affecting this region, including eastern boundary wave reflections. It is evident from this wide variety of theoretical, modeling, and empirical studies that, despite progress made during TOGA on understanding the ENSO cycle, there are many as-of-yet unresolved issues related to the coupled ocean-atmosphere interactions that require further investigation.
Figure 13: (left) Longitude-time distribution of 4°N–4°S averaged SST. Contour interval is 1°C, except for the 28.5°C isotherm. Superimposed as thick lines are the trajectories of two hypothetical drifters moved by 4°N–4°S averaged surface current anomalies derived from Geosat data (thick solid lines correspond to the total currents; thick dashed lines correspond to the Kelvin and Rossby wave contributions). (right) Longitude-time distribution of 4°N–4°S averaged surface current anomaly derived from Geosat. Contour interval is 10 cm s-1. Solid (dashed) lines denote eastward (westward) current anomalies. Thick solid and thick dashed lines are as in Figure 13 (left). From Picaut and Delcroix [1995].
The Kelvin waves most prominent in equatorial Pacific time series data have energy across a broad band of periods spanning roughly 40–120 days, with maximum energy concentrated near periods of 60–90 days. Sea level, thermocline depth, and zonal currents associated with these waves propagate eastward with 2–3 m s-1 phase speeds [Enfield, 1987; McPhaden and Taft, 1988; Johnson and McPhaden, 1993a, b]. Vertical structures suggest significant energy in both the first and second vertical modes [Kessler and McPhaden, 1995b], consistent with model simulations [e.g., Busalacchi and Cane, 1985; Giese and Harrison, 1990; Kindle and Phoebus, 1995]. There is also evidence that the wave structures are modified by wave-mean flow interactions [Johnson and McPhaden, 1993a, b]. Upon reaching the eastern boundary, the waves can be traced along the coasts of North and South America as coastal Kelvin waves [Spillane et al., 1987].
These Kelvin waves are forced primarily by surface zonal wind variations associated with westerly wind bursts and the Madden and Julian Oscillation in the western Pacific (Figure 11). The amplitude of the ocean wave response depends on the structure of the wind forcing, namely its temporal evolution, zonal fetch, and meridional structure [Knox, 1987; Harrison and Giese, 1991; Giese and Harrison, 1991]. In terms of frequency content, wave energy is concentrated at periods decidedly longer than the dominant 30–60-day period of the wind forcing itself [McPhaden and Taft, 1988]. Kessler et al. [1995] explain this "red shift" as the result of a scale selection process related to wind fetch, which favors excitation of the lower-frequency Kelvin waves in response to wind forcing in the intraseasonal band. Their results are analogous to Knox's [1987] analysis in the time domain, which indicated that an equatorial wind event of duration T and zonal fetch L, would lead to a Kelvin pulse of longer duration T + L/c, where c is the zonal phase speed of the Kelvin wave.
Intraseasonal Kelvin waves affect SST in the equatorial Pacific in a variety of ways. They can warm SST by zonal advection in the equatorial cold tongue as documented for the 1986–1987 El Niño [Johnson and McPhaden, 1993a] and the 1991–1993 El Niño [Kessler and McPhaden, 1995a]. Downwelling Kelvin waves also depress the thermocline [McPhaden and Hayes, 1990b; Kessler et al., 1995], which can lead to surface warming by reducing the efficiency of local wind-driven upwelling to cool the surface. Lien et al. [1995] found that the passage of a downwelling Kelvin wave during the 1991–1992 El Niño led to a reduction in upper ocean turbulent mixing in the central equatorial Pacific, which would likewise favor the development of warm SST anomalies.
There is a notable relationship between enhanced intraseasonal variability and El Niño in both the ocean and atmosphere [e.g., Keen, 1982; Luther et al., 1983; Lau and Chan, 1986; Enfield, 1987; McPhaden and Hayes, 1990b; Kessler et al., 1995; Kindle and Phoebus, 1995]. During El Niño westerly wind bursts tend to be more prominent, deep convection associated with the Madden and Julian Oscillation tends to be stronger and extend farther eastward along the equator in the Pacific, and intraseasonal equatorial Kelvin waves tend to be of larger amplitude. These findings have led to suggestions that intraseasonal variability, rather than chaotic interactions of the seasonal cycle with itself (see section 3.1), may be responsible for the irregularity of the ENSO cycle [e.g., Zebiak, 1989].
Nonlinear interactions between the ocean and the atmosphere are necessary to couple intraseasonal variations to the ENSO cycle. Harrison and Schopf [1984] proposed a mechanism whereby zonal advection by short-period Kelvin waves could initiate low-frequency warming in the equatorial cold tongue of the eastern and central Pacific, and some coupled models bear out the potential for this mechanism to trigger an El Niño [Latif et al., 1988]. Likewise, Kessler et al. [1995] described how intraseasonal Kelvin waves can contribute to the slow eastward displacement of the western Pacific warm pool, which would favor the development of warm El Niño SST anomalies.
The importance of the local response to strong westerly wind burst forcing in the western Pacific warm pool was first highlighted by Lukas and Lindstrom [1991]. That study and related work ultimately contributed to the design and implementation of the TOGA Coupled Ocean Atmosphere Response Experiment (COARE) [Godfrey et al., this issue]. Westerly wind bursts typically occur during the westerly phase of the Madden and Julian Oscillation [Sui and Lau, 1992], during which surface westerlies may attain speeds of 5–10 m s-1. These wind events lead to dramatic zonal current reversals in time and depth in the upper 100–150 m of the water column [McPhaden et al., 1988a, 1992; Delcroix et al., 1993; Kuroda and McPhaden, 1993; Kutsuwada and Inaba, 1995; Ralph et al., 1997]. The surface flow accelerates eastward and can reach speeds of over 100 cm s-1 in the course of a week. The resultant jet may extend over 40° of longitude, with anomalous eastward transports of 50 Sverdrups (1 Sv = 106 m3 s-1) between 5°N and 5°S. Westerly wind bursts and the westerly phase of the Madden and Julian Oscillation are usually associated with a drop in SST due to increased latent heat flux and reduced insolation [McPhaden and Hayes, 1991; Weller and Anderson, 1996; Cronin and McPhaden, 1997]. Strong wind forced currents advecting fresher water from the west, in combination with enhanced precipitation, generally lead to a freshening of the surface layer near the equator in the warm pool region. These processes can lead to barrier layer formation [Sprintall and McPhaden, 1994; Roemmich et al., 1994; Anderson et al., 1996], which Lukas and Lindstrom [1991] hypothesized as important for understanding the evolution of ENSO warm events. Wind burst forcing also excites downwelling equatorial Kelvin waves which propagate into the eastern Pacific as discussed in the previous section.
Tropical instability waves, first observed in the Pacific in satellite SST imagery [Legeckis, 1977], typically propagate westward with zonal wavelengths of 800–2000 km and periods of 20–30 days. They have been observed in ocean currents, temperatures, and salinity [Philander et al., 1985; Pullen et al., 1987; Halpern et al., 1988; McPhaden et al., 1990c; Kessler and McPhaden, 1995a; Qiao and Weisberg, 1995; McPhaden, 1996; Flament et al., 1996]. They are also detectable in Geosat and TOPEX/POSEIDON altimetry data [Perigaud, 1990; Giese et al., 1994; Busalacchi et al., 1994] despite the relatively coarse temporal resolution of altimeters compared to the basic frequency of the waves. Instability waves are seasonally and interannually modulated, being weakest during boreal spring and during the warm phase of ENSO. The waves derive their energy from the large-scale, seasonally varying zonal equatorial currents through shear instability [Philander, 1978; Cox, 1980; Philander et al., 1986; Luther and Johnson, 1990] and possibly through SST frontal instabilities [Yu et al., 1995]. As such, they are a significant source of drag on the South Equatorial Current and Equatorial Undercurrent, and they heat the cold tongue through large downgradient (i.e., equatorward) eddy heat transports [Hansen and Paul, 1984; Bryden and Brady, 1989]. The waves also affect the stability of the atmospheric boundary layer [Hayes et al., 1989b], the distribution of cloudiness [Deser et al., 1993], latent heat fluxes [Zhang and McPhaden, 1995], and the distribution of nutrients, pCO2, and other chemical species in the eastern equatorial Pacific [Feely et al., 1994]. Instability waves of similar character have been documented in the equatorial Atlantic, where they are evident during the boreal summer season [e.g., Weisberg and Weingartner, 1988; Musman, 1992]. They are a potentially significant source of aliased energy which, if unresolved (as in infrequently sampled shipboard data), add noise contamination to lower-frequency signals of climatic interest [Hayes and McPhaden, 1992; Kessler et al., 1996].
Wyrtki [1987] first attempted to monitor the variations of the throughflow by computing the large-scale pressure gradient between the western Pacific and eastern Indian Oceans. Davao in the Philippines was used for the western Pacific, and Darwin in Australia was used for the eastern Indian Ocean. He found that this difference was dominated by seasonal variations but that the two records were coherent at interannual timescales, resulting in a small difference on ENSO timescales. Later, Clarke [1991] modeled the reflection and transmission of large-scale, low-frequency waves at a gappy western Pacific boundary and found that the interannual sea level variations along northern Australia were in fact of Pacific origin. These results implied that the Davao-Darwin sea level difference was not an appropriate index for the throughflow at interannual timescales. Clarke and Liu [1993, 1994] argued that a better index of the throughflow would be based on differences between northern and southeastern Indian Ocean sea levels. Their index suggested that the throughflow increased during cold ENSO events and decreased during warm events.
Thermal structure associated with the Indonesian throughflow in the eastern Indian Ocean has marked interannual variations, which have been documented on a frequently repeated XBT line between Shark Bay (northwestern Australia) and Sunda Strait (Java) [Meyers, 1996]. The largest variations of dynamic height and depth of the thermocline are near the coast of Australia (Figure 14, left), and they are highly correlated to the ENSO signal in the western equatorial Pacific (Figure 14, right). The XBT observations are consistent with the study by Clarke and Liu [1994] and with their model of the generation of the variations by wind forcing with long timescales. The XBT measurements also document how the signal extends into the ocean interior and how it is related to variations on the coast of Indonesia. The observations and model consistently indicate that variations near the coast of western Australia are generated by winds over the equatorial Pacific, while variations near the coast of Indonesia are generated by winds over the equatorial Indian Ocean. The differences in vertically integrated dynamic height between the coasts of Australia and Indonesia are a measure of the transport of Indonesian throughflow. The estimated mean transport, based on XBT data, is 7 Sv [Meyers et al., 1995]. Consistent with the tide gauge measurements, the throughflow is weaker during El Niño, with a peak-to-trough amplitude on interannual timescales of transport in the upper 400 m of about 5 × 106 m3 s-1. What impact ENSO timescale variations in throughflow have on the climate of the Indian Ocean region is, however, unclear.
Figure 14: Joint empirical orthogonal functions (EOFs) of anomalies of SST, dynamic height (0–400 dbar) and depth of the 20° isotherm on a frequently repeated XBT line between Shark Bay (westernmost point of Australia) and Sunda Strait (western end of Java). (left) The first EOF (34% of the variance) shows the ENSO signal entering the Indian Ocean along the coast of Australia. (right) The temporal coefficients of the first EOF are highly correlated with the Southern Oscillation Index (SOI). From Meyers [1996].
Although the TOGA observing system focused primarily on the ENSO phenomenon in the tropical Pacific, satellite and some in situ measurement programs (e.g., VOS, tide gauges, and drifters) provided a global perspective on climate variations during the TOGA decade. In this section we briefly review studies of climate phenomena facilitated by measurements outside the tropical Pacific, with emphasis on variability related to ENSO.
Atmospheric teleconnections associated with the ENSO cycle affect oceanic variability in wide-ranging parts of the globe. Over the North Pacific Ocean, for example, the Aleutian Low becomes anomalously strong during the late fall and winter of an El Niño year. Associated with these changes in atmospheric pressure, the axis of the subtropical jet stream splits, one branch displaced southward, steering storms into the southwestern United States, and another branch displaced northward into the Pacific Northwest. Air-sea heat exchange is enhanced at midlatitudes by these changes in atmospheric circulation [Alexander, 1992], leading to cold open ocean SST anomalies during El Niño years [Wallace et al., this issue]. Along the west coast of the United States, on the other hand, anomalous alongshore southerly winds during El Niño can lead to reduced coastal upwelling, which contributes to warmer coastal SSTs and higher coastal sea level [Enfield and Allen, 1980; Ramp et al., 1997, and references therein].
In addition to this atmospheric teleconnection pathway between the tropical and midlatitude Pacific Ocean, equatorial oceanic Kelvin waves impinge on the eastern boundary, forcing poleward propagating coastal Kelvin waves in both hemispheres [Enfield and Allen, 1980; Chelton and Davis, 1982; Clarke, 1992; Clarke and Van Gorder, 1994; Ramp et al., 1997; Shaffer et al., 1997]. Roach et al. [1989] concluded that these signals dominate sea level variability as far north as San Francisco. These waves are particularly energetic at intraseasonal periods [Spillane et al., 1987]. Recently, Jacobs et al. [1994] found that Rossby wave signals forced at the eastern boundary by the passage of El Niño-related coastal Kelvin waves associated with the 1982–1983 El Niño could be detected in the central and western North Pacific a decade later. Jacobs et al. [1994] speculated that these Rossby waves contributed to the development of SST anomalies in the midlatitude North Pacific by rerouting the warm, normally eastward flowing Kuroshio Extension off Japan to a more northeasterly course in the early 1990s.
White and Peterson [1996] have recently detected a 4–5-year eastward propagating, zonal wave number two oscillation encircling the globe in the Antarctic Circumpolar Current. The wave is characterized by coherent oscillations in SST, sea level pressure, meridional winds, and sea ice extent. White and Peterson [1996] hypothesized that this wave may be related to forcing associated with El Niño through atmospheric teleconnections between the tropical Pacific and the Southern Ocean.
The tropical Atlantic is characterized by a prominent mean seasonal cycle in surface winds, sea level upper ocean currents, and temperatures [e.g., Carton and Katz, 1990; Reverdin et al., 1991a, b; Molinari and Johns, 1994; Katz et al., 1995b]. In addition, two important modes of interannual-to-decadal variability are evident around this seasonal cycle, one of which consists of warm events with variability concentrated near the equator [Philander, 1986; Houghton, 1991; Zebiak, 1993; Carton and Huang, 1994] and another of which consists of interhemispheric variations in tropical SST [Moura and Shukla, 1981; Servain, 1991; Houghton, 1991; Houghton and Tourre, 1992]. Dynamics intrinsic to the ocean-atmosphere-land system in the Atlantic basin are important in determining the variability associated with these low-frequency climate signals. However, ENSO teleconnections through the atmosphere influence their evolution as well, as discussed by Servain [1991], Delecluse et al. [1994], and Enfield and Mayer [1997].
Variability in the Indian Ocean is dominated by a pronounced seasonal cycle related to monsoon wind forcing [Rao et al., 1989; Molinari et al., 1990; Perigaud and Delecluse, 1992; Mizuno et al., 1995; Donguy and Meyers, 1995, 1996a; Meyers et al., 1995]. However, interannual anomalies on ENSO timescales are detectable as well [e.g., Perigaud and Delecluse, 1993; Tourre and White, 1995]. Tourre and White's [1995] simultaneous analysis of upper ocean thermal data in all three tropical ocean basins indicated what appeared to be a coherent eastward propagating interannual wave in upper ocean heat content near the equator. On the strength of this result they suggested the possibility of oceanic precursors to ENSO in the Indian Ocean thermal field, in addition to atmospheric precursors believed to be important in association with the monsoons [Webster and Yang, 1992]. Latif and Barnett [1995], on the other hand, argued that the Pacific forces the tropical Indian and Atlantic Oceans remotely through atmospheric teleconnections on ENSO timescales and that this forcing accounts for a significant percentage of the observed thermal variability described by Tourre and White [1995].
For the three tropical oceans, long-term averaged sea surface salinity (SSS) exhibits well-documented minima associated with the Intertropical Convergence Zones as well as relatively high salinities, mainly where evaporation significantly exceeds precipitation. Maximum seasonal SSS variations are found primarily in the Intertropical Convergence Zones and in the South Pacific Convergence Zone, in close relation to seasonal variations in rainfall [Delcroix and Henin, 1991; Dessier and Donguy, 1994; Donguy and Meyers, 1996b]. There is also notable ENSO-related SSS variability. During El Niño periods the SSS field west of about 150°W is characterized by fresher than average SSS within 8°N–8°S; conversely, saltier than average SSS is found poleward of 8° latitude [Delcroix and Henin, 1991; Delcroix et al., 1996]. There is also significant freshening of the surface layer in the eastern Pacific within 10° of the equator during El Niño, particularly east of 110°W [Ando and McPhaden, 1997]. SSS anomalies of reverse sign are observed during La Niña periods. In the equatorial band these interannual modifications in the salinity field result mainly from the combined effects of rainfall and horizontal salt advection, the latter process apparently dominating west of about 165°E [Picaut et al., 1996; Delcroix and Picaut, 1998; Ando and McPhaden, 1997; Henin et al., 1998].
Lukas and Lindstrom [1991] proposed that salinity variability of the upper ocean may be an important determinant in the evolution of ENSO. They hypothesized that in regions of heavy rainfall, thin surface mixed layers form which are isolated from the upper thermocline by salt stratified "barrier layers." The creation of these barrier layers potentially reduces the efficiency of vertical turbulent mixing to entrain cold thermocline water into the surface layer, except during periods of strong winds. Thus, barrier layer formation would favor warm SSTs in regions of heavy rainfall, thereby coupling the hydrologic cycle to the upper ocean heat balance.
Barrier layers have been detected in all three tropical oceans. They vary in thickness and location seasonally [Sprintall and Tomczak, 1992] and on ENSO time scales in the Pacific [Delcroix et al., 1992; Sprintall and McPhaden, 1994; Ando and McPhaden, 1997]. Processes responsible for their formation, and how the salt and heat balances of the upper ocean are coupled in the western Pacific warm pool, were major research themes of TOGA-COARE [Godfrey et al., this issue]. The results of TOGA-COARE, combined with ENSO predictability studies (e.g., Ji, M., R. W. Reynolds, and D. W. Behringer, Use of TOPEX/POSEIDON sea level data of ocean analyses and ENSO prediction: some early results. submitted to the Journal of Climate, 1998), may indicate the need for an improved network of long-term sustained ocean salinity observations for both ENSO prediction and climate diagnostics.
During the decade of TOGA several studies have shown that the ENSO signal extends through the tropical troposphere into the lower stratosphere [Gage and Reid, 1987; Reid et al., 1989; Gage et al., 1993]. In other words, the atmospheric response to changing patterns of sea surface temperature extends to high altitudes owing to the influence of tropical convection. Diabatic heating associated with latent heat release and radiative effects of clouds have a profound influence on even the largest-scale circulation systems in the atmosphere [Hartmann et al., 1984; Houze, 1989; Mapes and Houze, 1995].
The Christmas Island wind profiler (Figure 5) has been in place long enough to observe many annual cycles and a few ENSO cycles of the zonal winds. A time-height cross section of zonal winds observed at Christmas Island is shown in Figure 15. While the mean zonal winds in the tropics are usually easterly, we observe substantial westerlies recurring periodically in the upper troposphere. These westerlies develop on an annual basis during the northern hemisphere winter months. Note that the strongest upper tropospheric westerlies are seen during the La Niña or cold event of 1988–1989. By way of contrast the upper tropospheric westerlies are relatively weak during the El Niño years of 1986–1987, 1991–1992, and 1994–1995. These observations are consistent with a strengthening of the Walker circulation during cold events and a weakening of the Walker circulation during warm events.
Figure 15: Time-height cross section of Christmas Island zonal winds, April 1986 to April 1995. After Gage et al. [1996b].
The mean annual variation of tropospheric zonal winds observed at Christmas Island is reproduced in Figure 16. The upper tropospheric westerlies are seen to occur above about 7 km and are seen to be strongest during March–May and November–December. Zonal winds over Christmas Island are typically easterly at all heights during the northern summer. The annual variation of the zonal winds observed at Christmas Island is in phase with the annual cycle of tropical convection over the western Pacific and is consistent with a strengthening and weakening of the Walker circulation driven by convective heating over the western Pacific warm pool region [Gage et al., 1996b]. The depth of the upper tropospheric westerlies is likely due to the deep tropical heating associated with mesoscale convective systems [Hartmann et al., 1984].
Figure 16: Low-pass-filtered composite annual cycle of zonal winds observed at Christmas Island. After Gage et al. [1996b].
Vertical motions are rarely observed directly in the atmosphere [Balsley et al., 1988]. This is partly due to the difficulty in measuring very small motions, but the measurement problem is complicated by the presence of internal gravity waves that can mask the small long-term mean vertical motions or otherwise bias observations [Nastrom and VanZandt, 1994]. Wind profiler direct measurements of vertical velocities in the tropics have confirmed some expectations at the same time they have raised new questions. The principal finding is that in the absence of convection the troposphere is generally subsiding at a fraction of a cm s-1. The adiabatic warming consistent with the observed magnitude of subsidence is what is required to balance radiative cooling to space [Gage et al., 1991b].
While they have not been in use as long as the VHF profilers, the UHF profilers have already proven to be valuable tools for atmospheric research [Angevine et al., 1993, 1994; Rogers et al., 1993; Gage et al., 1994b, 1996a]. High-resolution time and height observations by UHF profilers have improved our knowledge of vertical structure and temporal variability of lower tropospheric winds in the tropics [Gutzler et al., 1994; Parsons, 1994]. For example, Deser [1994] and Gutzler and Hartten [1995] have used the profiler observations to obtain a more complete picture of the daily variability of the lower tropospheric winds at a number of locations in the Pacific.
Recently, it has become evident that UHF profilers can provide valuable information about precipitating cloud systems [Gossard, 1988; Rogers et al., 1993; Gage et al., 1994b, 1996a; Ecklund et al., 1995; Williams et al., 1995]. In the presence of precipitating loud systems the height coverage of the profilers is greatly increased. With the large amounts of data obtained from the tropics using UHF profilers at a number of locations, it is now possible to begin to construct the climatology of precipitating cloud systems in the western Pacific. Used in conjunction with a VHF profiler, the UHF profiler can provide precipitation fall speeds relative to background vertical air motions [Currier et al., 1992].
TAO data have also been of value in studies of atmospheric dynamics. For example, Hayes et al. [1989b] found that in addition to forcing of boundary layer winds by horizontal pressure gradients, as hypothesized by Lindzen and Nigam [1987], stabilization of the boundary layer over the cold tongue tends to reduce mixing of wind momentum downward from aloft, particularly in the meridional direction as hypothesized by Wallace et al. [1989]. Accounting for these variations in vertical stability in diagnostic studies allows for a more dynamically consistent interpretation of oceanic effects on boundary layer winds in the equatorial Pacific [Nigam and Chao, 1996].
Zhang [1996] used TAO data to document surface manifestations of the Madden and Julian Oscillation in the atmospheric boundary layer of the western Pacific. He found inconsistencies, as did Jones and Gautier [1995] and Flatau et al. [1997], between observations from the western Pacific and theories for these oscillations. As a result, Flatau et al. [1997] proposed a new theory involving interactive SST feedbacks on convection at intraseasonal time scales. Their modified theory allowed for time varying SST feedbacks to the atmosphere in response to intraseasonal heat flux forcing of the ocean, which led to a better simulation of the Madden and Julian Oscillation in a simple coupled ocean-atmosphere model.
TAO data have been used to examine the role of mesoscale enhancement of surface turbulent fluxes [Zhang, 1995; Esbensen and McPhaden, 1996] and the related issue of convection-evaporation feedbacks [Zhang et al., 1995]. The role of evaporation in limiting long-term mean SST in the western Pacific warm pool was described by Zhang and McPhaden [1995]. They found that above 29°C, latent heat flux decreases with increasing SST, lending credence to the "thermostat" hypothesis [Ramanathan and Collins, 1991], which suggests cloud-radiative feedbacks are the primary limiting factor in determining maximum warm pool SSTs.
Process-oriented studies embedded in the TOGA observing system included the Tropical Pacific Upper Ocean Heat and Mass Budgets (TROPIC HEAT) Experiments (I in 1984–1985 and II in 1987) to examine the processes controlling SST in the equatorial eastern Pacific [Eriksen, 1985; Hebert et al., 1991], the Western Equatorial Pacific Ocean Circulation Study (WEPOCS) in 1985–1988 to examine complex current structures in a relatively poorly explored part of the tropics [Lindstrom et al., 1987], the Tropical Instability Wave Experiment (TIWE) in 1990–1991 to study the life cycle and energy sources for tropical instability waves in the eastern Pacific [Qiao and Weisberg, 1995; Flament et al., 1996], TOGA COARE in 1992–1994 to study ocean-atmosphere interactions in the western equatorial Pacific [Godfrey et al., this issue], the Joint Global Ocean Flux Studies (JGOFS) Equatorial Pacific (EqPac) experiment in 1992 to study biogeochemical cycling in the equatorial Pacific [Murray et al., 1994], and the Central Equatorial Pacific Experiment (CEPEX) in 1993 to study cloud radiative feedbacks and their impacts on SST [Ramanathan et al., 1995].
The TOGA observing system provided a broad geographical perspective and long time history to aid in the interpretation of the measurements from these shorter-duration, regional-scale field programs. For example, the intensive observing period of TOGA COARE took place in the western Pacific from November 1992 to February 1993, during a hiatus in El Niño conditions in the eastern equatorial Pacific (Plate 1 and Figure 11). The JGOFS experiment, on the other hand, started during the 1991–1992 warm event but concluded during near-normal conditions at the end of 1992.
In many cases the TOGA observing system was enhanced to facilitate these process studies. During the enhanced monitoring phase of TOGA COARE in 1992–1994 additional TAO moorings were deployed west of the date line to provide finer than 10° zonal resolution of surface winds, upper ocean temperatures, and currents along the equator [Webster and Lukas, 1992]. Several TAO moorings in the western Pacific were also equipped with special sensors to measure salinity, rainfall, and incoming shortwave radiation in an effort to better understand surface fluxes in relation to upper ocean variability [Cronin and McPhaden, 1997]. After TOGA COARE ended, some of these measurements continued in the western Pacific warm pool [e.g., Koehn et al., 1996]. Drifting buoy deployments also increased west of the date line during TOGA COARE [Ralph et al., 1997], and some of these drifters were equipped with salinity sensors. Enhancements of the WWW included installation of integrated sounding systems (ISS) at Manus Island, Nauru, and Kapingamarangi in 1992 prior to TOGA COARE [Gutzler and Hartten, 1995], with the Manus Island and Nauru sites continuing after COARE ended.
Specific enhancements to other process studies included specially instrumented TAO current meter moorings at 0°, 140°W during TROPIC HEAT, and TIWE provided support for the hypothesis that internal waves mediate the diurnal cycle of vertical mixing along the equator [McPhaden and Peters, 1992; Moum et al., 1992; Lien et al., 1996]. During TIWE, moored data were used to estimate diurnally varying vertical heat fluxes associated with that mixing [Bond and McPhaden, 1995], and a large number of drifters were deployed to provide additional information on the structure of instability waves [Flament et al., 1996]. Moored and drifting buoys were deployed with bio-optical sensors during JGOFS to document physical controls on primary productivity in the equatorial Pacific [Foley et al., 1998].
At the outset of TOGA the modeling and observational activities were relatively separate components of the program. However, as the program matured, a number of factors contributed to the development of a mutual dependency between TOGA models and observations. At a very basic level, data were needed for the development and validation of oceanic, atmospheric, and coupled models. Moreover, as experimental forecasts of ENSO became more routine and as initialization and assimilation techniques for coupled models took on greater importance, the modeling and observational components of TOGA developed a more intricate relationship. Overviews of the interaction between tropical models and data can be found in work by Latif et al. [this issue] and Stockdale et al. [this issue] and in the reviews by Knox and Anderson [1985], Philander [1990], and McCreary and Anderson [1991]. We concentrate here specifically on the evolution of this partnership toward improved model-based analyses and better coupled model initial conditions for predictions.
When considering the initialization of tropical ocean models and coupled prediction models, there are several factors that are critical. First, the tropical oceans are to a certain extent deterministic, by which we mean that adequate knowledge of past forcing in principle allows us to largely determine the state of the ocean. Knowledge of the surface wind stress is paramount in this determination. For example, Busalacchi and O'Brien [1980, 1981] demonstrated that, with a reduced gravity model and surface stress, one could capture key aspects of sea level variability associated with ENSO. Studies with ocean general circulation models (OGCMs) [e.g., Philander and Seigel, 1985; Harrison et al., 1990] also emphasized the paramount importance of wind forcing in model simulations. This fact makes the analysis and initialization problem quite different from that of numerical weather prediction, where there is no counterpart to the external forcing (and its associated errors) that are imposed through surface wind stress.
While in theory it is feasible that coupled tropical forecast models could be initialized with wind stress alone, practical considerations suggest that ocean thermal data will also be important. This is because wind stress and upper ocean thermal structure are partially redundant, so that observing and initializing baroclinic equatorial wave modes with subsurface temperature data could help correct some of the deficiencies in the imposed wind forcing. SST observations, either through assimilation or via surface boundary constraints, have also been important for the development of both the atmospheric and oceanic components of coupled prediction models. The ready availability, spatial coverage, and accuracy of SST analyses makes this variable particularly valuable for model validation and development [e.g., Stockdale et al., 1993].
From a historical perspective, sea level data has made one of the more significant contributions to ocean model development, particularly as equatorial theory was developing prior to TOGA. In situ sea level data continue to provide important model validation, particularly as sea level variations represent an integral, low baroclinic mode response to wind forcing and thermodynamic adjustments. With the advent of satellite altimetry, giving the spatial coverage not possible with in situ instrumentation, sea level may well assume far greater importance for model initialization.
Early studies in TOGA pointed to the advantages of thermal (mass) information vis-a-vis velocity information for ocean model initialization [Moore et al., 1987; Philander et al., 1987]. Hence, in a modeling context, velocity data have been used mostly for validation purposes [e.g., Leetmaa and Ji, 1989; Brady and Gent, 1994; Chen et al., 1994b; Fukumori, 1995; Halpern et al., 1995; World Climate Research Program, 1995a]. Various other data sets, such as those for salinity and surface heat fluxes, have also played important though somewhat less critical roles in model development. Consistent with these considerations and with the discussion in section 2.2 the National Research Council [1994a] ranked measurements in the following order of importance for the purpose of short-term climate prediction: (1) wind stress and SST, (2) subsurface thermal data, (3) sea level and ocean current data, and (4) salinity and atmospheric boundary layer data.
One of the focuses through the early part of TOGA was the assessment of the quality of various wind stress products. It was known that VOS winds would be useful but likely inadequate, but it was not immediately clear whether improved analysis techniques and improved numerical weather prediction schemes would make up for some of these inadequacies [e.g., Reynolds et al., 1989a]. Harrison et al. [1989] used a tropical ocean general circulation model to diagnose the impact of differences in various wind stress products. They compared simulations of the 1982-1983 El Niño forced by the Sadler and Kilonsky [1985] wind analysis (produced from VOS wind data and cloud drift winds), the FSU wind analysis [Goldenberg and O'Brien, 1981], and three analyses based on numerical weather prediction models (ECMWF, National Meteorological Center (NMC), and Fleet Numerical Oceanography Center (FNOC)). Overall, the research analyses [Goldenberg and O'Brien, 1981; Sadler and Kilonsky, 1985] produced more realistic dynamic responses but less convincing SST results for the equatorial waveguide. Simulations of the mean seasonal cycle and the 1982-1983 El Niño using linear dynamical ocean models [McPhaden et al., 1988b; Busalacchi et al., 1990] yielded similar results with regard to ocean dynamical responses, namely that the research products led to more realistic results. Details aside, one of the most important conclusions of these studies as far as TOGA was concerned was that improved knowledge of the surface wind stress was essential.
Operational atmospheric weather analysis and forecast models routinely merge observations of different parameters (e.g., temperature, winds, etc.) made at different levels in the atmosphere using different instruments. These analysis and forecast systems produce a dynamically consistent model atmosphere with high temporal and spatial resolution. For this reason the surface wind fields from such systems are often used to force ocean models like that run at NCEP for near-real-time tropical ocean analyses. Improving the quality of operational atmospheric model-based wind analyses is therefore an issue of some importance to climate modelers.
Operational centers now routinely use either wind speeds from the DMSP SSM/I instrument and/or vector winds from the ERS-1 and recently launched ERS-2 scatterometers. For example, the U.S. Navy [Phoebus and Goerss, 1991] and NCEP [Yu and Deaven, 1991] use the SSM/I wind speeds, while ECMWF [Gaffard and Roquet, 1995] and NCEP [Peters et al., 1994] use the ERS-1 and ERS-2 vector winds. The SSM/I winds are converted to vector winds using directions assigned from either the model forecast or a combination of the forecast and available data. Phoebus et al. [1994] reported that the greatest impact of the SSM/I was in the tropics and at higher latitudes along the meteorological storm tracks. Gaffard and Roquet [1995] found that the ERS-1 and ERS-2 vector winds improved the analyses in the southern hemisphere and had some positive impact in the short-range forecast.
TAO data are also used in operational weather forecast systems. Impact studies done at ECMWF, as reported by Anderson [1994], showed that differences between ECMWF analyses with and without TAO winds could exceed 3 m s-1, although typical differences were less. In addition, the impact of TAO observations tended to weaken significantly if the model was not reinforced with new TAO observations every 6 hours. Anderson [1994] pointed out that, in general, single level surface data like those from TAO buoys can be expected to have a relatively low impact on the atmospheric weather analyses. Reynolds et al. [1989a] reached a similar conclusion in a comparison of surface winds from the buoys with the winds from several different operational analyses. They found that the analyses looked more like each other than like the data. However, the models themselves have problems, as pointed out in a study by Williams et al. [1992]. They compared wind profile data at Christmas Island with the ECMWF forecast model and found that the model and the data were consistent above 1.5 km but not below this level. The model winds at these lower elevations were too weak and did not properly turn with height. This result suggests that there are problems in the model tropical boundary layer and that model and analysis systems need to be improved to optimize assimilation of tropical surface winds.
Recently, TAO and other TOGA-related data sets have been incorporated into atmosphere reanalyses at NCEP, ECMWF, and NASA Goddard Space Flight Center. These decade-long, internally consistent model analyses are produced using state-of-the-art numerical models, assimilation systems, and the most complete data sets available from historical archives [e.g., Schubert et al., 1993; Kalnay et al., 1996]. These analyses are valuable for providing initialization and validation fields for coupled model predictability studies, for determining the sensitivity of atmospheric models to slow variations in the surface boundary conditions, and for diagnostic studies of atmospheric variability. Evaluations of these reanalyses products are currently underway [e.g., Saha et al., 1995; Smull and McPhaden, 1996].
Availability of TAO data has led to efforts to develop improved surface wind analyses for ocean modeling through blending of buoy data with ship winds, satellite winds, and/or model output. Two studies illustrate this approach and the impact that TAO data make on such analyses. Menkes and Busalacchi [1995] performed a series of linear ocean model hindcasts for the equatorial Pacific using two baseline forcing functions over the period 1982–1993. The first, denoted CMP9, was based on winds derived from the NCEP medium-range forecast model as forced by observed SST but without incorporating any surface wind data or other meteorological data via an assimilation/analysis cycle. The other baseline wind product was the FSU winds. Beginning in November 1992, the FSU analyses incorporated TAO observations in increasing numbers (see Appendix B, section B1), but it is difficult to quantify the weight they were given in the subjective FSU analysis. Two combined data sets, CMP9 plus TAO and FSU plus TAO, were constructed by optimally interpolating the monthly TAO wind observations to each baseline forcing. Wind observations at each TAO location were converted to wind stress using the stability dependent parameterization of Liu et al. [1979]. Four sea level simulations were then performed and evaluated against tide gauge sea level measurements, gridded fields of TOPEX/POSEIDON sea level, and TOGA-TAO dynamic height anomalies across the equatorial Pacific Ocean.
The impact of TAO winds was characterized as a function of the increasing number of TAO observations with time. It was shown that the incorporation of a few TAO observations into the CMP9 wind product from 1987 onward compensated for the erroneously weak winds in the central and eastern equatorial Pacific and subsequently led to improved simulations (Figure 17). Similarly, the TAO observations also had a positive impact on the FSU simulation, both in terms of phase and amplitude, suggesting that the TAO observations be given greater weight in the FSU analysis. The impact of TAO observations in the 1990s, when the TAO array was reaching full deployment, was such that the improved simulations forced by FSU plus TAO and CMP9 plus TAO winds were quite similar, in contrast to earlier periods in the 1980s when the FSU and CMP9 simulations were very different.
Figure 17: Modeled sea level anomaly (SLA) versus observation at Santa Cruz, Galapagos Islands. (top left) CMP9 (dotted line) simulation versus observations (solid line). (top right) Same as Figure 17 (top left), but for CMP9 plus TAO (dashed line). (middle left) Same as Figure 17 (top left), with FSU (thin line). (middle right) Same as Figure 17 (top left), with FSU plus TAO (dot-dash line). (bottom) The correlation coefficient between the modeled and observed sea level anomalies as the time over which the correlation is computed progressively reduced by 1 year from its starting date (labeled on abscissa) to 1993. For example, the point labeled 1987 represents the cross correlation from 1987 through 1993.
A similar study was done by Reynolds et al. [1995] for the period April 1992 to April 1994. However, in this study they used the FSU product as well as two different monthly products: the lowest sigma level winds (roughly 40 m in height) from the NCEP operational medium-range forecast model with atmospheric data assimilation and ERS-1 wind stresses computed at a height of 10 m using the algorithm of Freilich and Dunbar [1993]. An objective analysis procedure [see Lorenc, 1981] was used to correct each of the wind fields with TAO data. Comparison of the corrections showed that all analyses tended to have zonal wind stresses that were too weak relative to TAO in the eastern tropical Pacific (Figure 18). Of the three wind products, however, the FSU analysis was in best agreement with TAO. NCEP stresses were too weak (i.e., consistently negative differences with TAO) during roughly the first half of the comparison period, although there appeared to be some improvement in the NCEP winds over the second half of the record. Conversely, the ERS-1 stresses were consistently too weak relative to TAO for the entire period.
Figure 18: Zonal wind stress differences relative to TOGA-TAO for three products: NCEP, FSU, and ERS-1. The differences are averaged over 10°N to 10°S and 180° to 100°W. After Ji and Leetmaa [1997].
Reynolds et al. [1995] also used an ocean model to evaluate the impact of these different wind products. However, in contrast to Menkes and Busalacchi [1995], they used the general circulation model reported by Ji et al. [1995] both with and without the assimilation of thermal data. Results showed that assimilation was able to compensate for wind stress differences. Without assimilation, though, the ocean model was more affected by the different wind stress forcing. In particular, it was possible to clearly determine that ERS-1 zonal wind stresses were too weak in the eastern equatorial Pacific. However, the differences in the model fields compared to observations could not clearly identify which of the remaining three products (NCEP, FSU, and NCEP corrected by TAO) was superior. The Menkes and Busalacchi [1995] and Reynolds et al. [1995] studies differ because different wind stress fields and different models were used. However, in combination these studies indicate that TAO data have the strongest positive impact on the wind stress fields that are most independent of the mooring data.
Implementation of the TOGA observing system provided unprecedented opportunity for studying large-scale, low-frequency climate variability through the application of data assimilation techniques in combination with simple and complex tropical ocean models. Keys to achieving this were the vastly improved data coverage from the TOGA observing system, more effective data management strategies allowing rapid access to observations, order-of-magnitude improvements in computing capacity and resources, and improvements in ocean models.
Prior to TOGA, most oceanic observations were obtained from VOS lines, a handful of moorings and circulation drifters, and occasional research cruises. With the exception of SST, which could also be retrieved from satellite, it was essentially impossible to produce basin-scale ocean analyses from observations alone. With increased data coverage during TOGA, including a greatly enhanced volunteer observing ship network and the TAO array in the equatorial Pacific, regular and routine subsurface ocean analyses became possible. Several centers, including the El Niño Monitoring Center of the Japan Meteorological Agency (JMA), NCEP, the Joint Environmental Data Analysis Center in the United States, and the Bureau of Meteorology Research Center (BMRC) in Australia, began routinely producing monthly subsurface maps, particularly for the tropical Pacific.
All the data analysis and assimilation systems depend on knowledge of the amplitude and spatial and temporal scales of variability. Scale analyses, such as those of Meyers et al. [1991], Festa and Molinari [1992], and Kessler et al. [1996], provided estimates of signal levels versus unresolvable noise as well as estimates of the spatial and temporal covariance of the resolvable signal (which allow realistic scales for interpolation to be set). While the practical application of such information is not always straightforward, particularly when the first guess is provided by a dynamical model, it does nevertheless represent the fundamental basis for most of the applications described below.
One example is the subsurface ocean analysis system developed at BMRC of Australia [Smith et al., 1991; Smith, 1995a]. This system uses optimal interpolation and a simple statistical forecast model to produce global upper ocean temperature analyses at periods from 10 days to 2 months, utilizing data from XBTs and TOGA-TAO. All quality control is objective [Smith, 1991] on the basis of information derived from the statistical interpolation. The shorter-period analyses were shown to retain all the important low-frequency, large-scale information of the bimonthly analyses (the analysis period upon which much of the TOGA observations were planned) as well as much of the interesting high-frequency fluctuations [Smith, 1995b]. Over monthly periods for the last half of TOGA, the estimated root-mean-square (rms) error variance in the 20°C isotherm analysis was typically 4–6 m (equivalent to around 0.3°C). Achieving such accuracy was a remarkable accomplishment, considering the low expectations for the measurement of subsurface thermal structure during TOGA as reflected in Table 4.
Dynamic ocean models have been used to simulate basin-scale ocean circulations long before TOGA. While such simulations did not usually ingest ocean information, they did represent an alternative route to ocean analyses, whereby information in the applied surface boundary forcing (principally the wind stress) was used to indirectly infer the state of the ocean. The main problems with model simulations were the poor quality of surface forcing, because of a lack of wind observations over the open ocean, and errors in the ocean model physical parameterizations. Limited in situ observations were primarily used for validation of model results. Although the quality of surface winds has improved steadily, especially since the TOGA observing system increased surface wind observations in the tropical Pacific, errors in the winds and in ocean models still significantly limit the accuracy of the simulations [Ji and Smith, 1995]. One way to compensate for errors in wind stress forcing and ocean model physics is to use data assimilation techniques to combine observations and model fields to yield the best possible estimate of the ocean state.
Data assimilation has been an active area of research from well before TOGA, although most practical applications were in the field of meteorology. Advances in ocean data collection, communication, and modeling in the late 1970s and early 1980s made ocean data assimilation a feasible option. Several studies have examined the problem of ingesting ocean subsurface data into simpler, linear, shallow water models of the tropical ocean [e.g., Moore, 1989, 1990, 1992; Moore et al., 1987; Moore and Anderson, 1989; Sheinbaum and Anderson, 1990a, b; Hao and Ghil, 1994; see also Busalacchi, 1996; Stockdale et al., this issue]. All these studies showed that subsurface sampling as practiced during TOGA could be used to correct model and wind-forcing errors and that the time taken for correction was only a month or so, owing to the rapid communication of information by equatorial waves.
An early attempt to produce routine ocean analyses utilizing an ocean data assimilation technique was a system developed by Leetmaa and Ji [1989] for the tropical Pacific. This system used wind-forced ocean model simulation as a first guess and combined the observations collected during a period of 1 month with the model field using the optimal interpolation. The data assimilation procedure was done monthly.
The main advantage to the model-based analyses is that large areas of data void are filled in by model dynamics. The main drawback to the sequential initialization method is that the data assimilation can introduce a strong shock when corrections are applied to the model fields, as discussed by Moore [1990]. Also, for models integrated forward in time until the next data assimilation cycle without continuous constraint by observations, model fields will drift toward the model's own equilibrium state. Hence a "sawtooth" pattern in the time history of the analyses is sometimes obvious [e.g., Hayes et al., 1989a].
A data assimilation system developed by Derber and Rosati [1989] was a significant improvement over earlier ocean analyses. This system is based on a variational method in which assimilation is done continuously during the model integration. Corrections to the model are spread over a long period of time; thus change to the model temperature field during each model time step is incremental. This significantly reduces the impact to the dynamical balances of the model fields and also keeps model fields from drifting toward their own climate. Further, an observation is retained in the model for a long period of time (2–4 weeks), weighted by the difference between the model time and the observation time during each assimilation time step. This procedure significantly increases the influence of observations to compensate for the lack of spatial and temporal data coverage in many areas. The drawback in doing this is that it tends to limit the analyses to resolving only large spatial scales and low-frequency phenomena [Halpern and Ji, 1993].
An operational model-based ocean analysis system based on the data assimilation system of Derber and Rosati [1989] has been implemented at the NCEP [Ji et al., 1995]. Real-time observations from satellite, VOS ships, and drifting and moored buoys are assimilated into an ocean general circulation model to produce near-real-time (weekly mean) Pacific and Atlantic analyses. The near-real-time NCEP ocean analysis system is forced with weekly averaged surface winds produced by the NCEP operational atmospheric analyses. Retrospective monthly Pacific Ocean reanalyses have also been generated at NCEP by forcing the ocean model with historical monthly wind-stress analyses produced at Florida State University [Stricherz et al., 1992] and incorporating additional delayed mode data not available in real time [Ji and Smith, 1995].
Shown in Figure 19 is the time history of the depth of 20°C isotherm anomalies along the equator in the Pacific for 1982–1995. The thermocline anomalies produced by the ocean analysis system (Figure 19, middle) showed variability in the central and western Pacific stronger than that produced by a model forced with the FSU winds without data assimilation (Figure 19, right). Comparisons with in situ observations of moorings and tide gauges suggest that the model-based analyses are of higher accuracy than the wind-forced simulation [Ji and Smith, 1995]. These studies show that even when using a high-quality wind stress forcing and a state-of-the-art ocean general circulation model, ocean data assimilation can still further improve the quality of analyses by compensating for errors in the forcing and model.
Figure 19: Anomalous depth of the 20° isotherm along the equator for the Pacific produced (left) by BMRC, (middle) by the NCEP ocean analysis system, and (right) by an ocean model simulation forced with monthly surface wind analyses from FSU. The contour interval is 10 m. Anomalies greater (less) than 20 m (-20 m) are indicated by dark (light) shading. From Ji and Leetmaa [1997].
Also shown in Figure 19 (left) are the 20°C isotherm depth anomalies from the BMRC subsurface analysis system, which is based on statistical analyses rather than dynamical model analyses [Smith, 1995b]. It should be noted that the NCEP and BMRC systems have quite different approaches to quality control (subjective versus objective) and to assimilation/inter- polation (continual insertion with variational con-straints versus sequential single-period optimal interpolation). The analyzed peaks and depressions of the thermocline depth from the NCEP and BMRC systems are generally similar (e.g., the peak anomalies of the 1982–1983 and 1991–1992 warm and 1984 cool events), as should be expected since they are essentially based on the same data sets. There are, however, some significant differences; the NCEP analysis of the 1984 cooling is characterized by a coherent west-to-east evolution, whereas the BMRC analysis shows essentially in-place cooling. Such differences reflect the different modes of interpolation; the dynamic system has theoretical advantages for transferring information within the equatorial waveguide but at the same time may be hampered by errors in the wind and/or the model.
A promising way of improving tropical ocean model-based analyses is through the assimilation of altimetry data [see, e.g., Arnault and Perigaud, 1992]. This requires projection of sea level variability onto baroclinic ocean thermal structure, which can be readily done by developing empirical relationships between the two variables [e.g., Rebert et al., 1985; Carton et al., 1996]. Advanced techniques such as the Kalman filter and the adjoint method have been used to assimilate Geosat and TOPEX/POSEIDON altimetry data into simple reduced-gravity models [e.g., Gourdeau et al., 1997; Greiner and Perigaud, 1994, 1996; Fu et al., 1993; Fukumori, 1995]. Impact studies of altimetry assimilation on ocean general circulation model-based analyses have also been performed Carton et al. [1996], and Fischer et al., 1997].
Assimilation of observations obtained from the TOGA observing system not only provides means to produce much improved ocean analyses, it also provides a great opportunity for improving the definition of the initial ocean fields for prediction of ENSO using coupled models. This is discussed in section 4.4. Analyses such as those described above have also found a wide range of other applications. For example, Lukas et al. [1995] studied the large-scale variations of the Pacific Ocean during TOGA COARE using the NCEP subsurface analyses, providing a context for the analysis of observations of air-sea interaction in the intensive flux array. The use of model-based analyses for process studies is now quite common in meteorology, and the advances in ocean analysis and assimilation during TOGA will assist in making such applications more common in climate studies.
Finally, analysis systems have been used to examine the design of the TOGA subsurface observing system. Miller [1990] investigated the impact that ocean thermal data (processed to estimates of dynamic height) might have in hindcasts of sea level in the equatorial Pacific. His results suggested that the TAO array would positively impact on hindcasts of monthly mean sea level. Smith and Meyers [1996] have examined the relative impact of XBT and TOGA-TAO data for monitoring tropical Pacific Ocean thermal variability. They concluded that for the last half of the TOGA period, over the region 20°S–20°N, the net information content of the systems were comparable in magnitude, each contributing the equivalent of around 300 independent subsurface samples per month.
ENSO prediction depends strongly on the accuracy of the ocean initial conditions. Three different methods are presently used for initialization of the ocean for ENSO predictions using coupled ocean-atmosphere models. The first method, used by Cane et al. [1986], is to spin up the ocean using the observed surface wind history prior to the initiation of a forecast. A second method uses assimilation of subsurface temperature data together with surface wind forcing to achieve better defined subsurface ocean states. This is done at the NCEP [Ji et al., 1994] and at the Geophysical Fluid Dynamics Laboratory (GFDL) [Rosati et al., 1997]. A third method developed at BMRC utilizes both wind and subsurface data jointly to initialize a coupled model through an adjoint data assimilation method [Kleeman et al., 1995].
Assimilation experiments described in the previous section illustrated the need to assimilate data in such a way that initialization "shock" is minimized. On the other hand, these studies demonstrated the potential impact of data assimilation on the forecast of eastern equatorial Pacific SSTs several seasons into the future. Ji and Leetmaa [1997], for example, compared results from forecast experiments initiated from ocean initial conditions produced with data assimilation and produced with wind forcing alone, using the NCEP coupled ocean-atmosphere forecast model [Ji et al., 1994]. Shown in Figure 20 are temporal anomaly correlation coefficients (ACC) and root-mean-square (rms) errors as a function of forecast lead times for area-averaged SST anomalies between forecasts and observations for an eastern equatorial Pacific region (120°–170°W, 5°S–5°N). The forecasts were initiated monthly for the period of 1983–1993. This comparison demonstrates convincingly that data assimilation has a significant positive impact on improving ENSO forecast skill. Ji and Leetmaa [1997] also showed forecast skills using ocean initial conditions produced with assimilation of XBT data alone and with assimilation of both XBT and TAO buoy data. The results indicate significant positive impact of the TAO buoy data, largely due to the vastly improved spatial and temporal data coverage by the TAO array in the tropical Pacific.
Figure 20: (left) Anomaly correlation coefficients and (right) rms errors between forecasts and observations for area-averaged SST anomalies in the eastern equatorial Pacific region between 170°–120°W and 5°S–5°N. Solid (dash-dot) lines are for forecasts initiated from ocean initial conditions produced with (without) subsurface data assimilation.
Kleeman et al. [1995] also demonstrated how enhanced forecast skill could be achieved in an intermediate coupled model by improving the initial conditions for upper ocean heat content. In this study the adjoint for the ocean component of the coupled model was used to improve the ocean initial conditions by finding a condition that was consistent with both the wind forcing and the subsurface ocean thermal data. Two sets of experiments were performed for the period January 1982 through October 1991. In the first experiment the ocean initial conditions were obtained by forcing the ocean model with the FSU winds. This initialization procedure was consistent with that of Cane et al. [1986], and similar forecast skill scores were obtained. In the second experiment improved initial conditions were obtained by using analyzed subsurface temperature anomalies averaged over the upper 400 m of the water column [Smith, 1995b] for the 12 months prior to initiating a coupled forecast. The use of the ocean data assimilation in this case led to notable increases in forecast skill.
Altimetry data, in addition to upper ocean thermal data, likewise have the potential for improving the skill of short-term climate predictions. [Fischer et al., 1997; M. Ji, R. W. Reynolds, and D. W. Behringer, Use of TOPEX/POSEIDON sea level data of ocean analyses and ENSO prediction: Some early results, submitted to the Journal of Climate, 1998]. In one set of experiments, for example, sea level data from TOPEX/POSEIDON were added to the XBT and TAO ocean model assimilation system of Ji et al. [1995]. The sea level data improved the agreement of the model sea level with independent tide gauge data and led to a more realistic forecast of tropical Pacific SSTs. On the other hand, predictability experiments using the Zebiak and Cane [1987] coupled model indicated that forecast errors were not reduced by using altimetry data for ocean model initialization [Cassou et al., 1996]. Thus, the utility of altimetry for initialization is model dependent, so that more research will be required to fully exploit altimetry for ENSO prediction.
In the previous initialization studies the oceanic component was first forced by observed wind stress and adjusted by assimilating subsurface thermal observations. Subsequently, the model-simulated SST was used to force the atmospheric component. However, a potential problem with this common approach is that since there are no interactions allowed between the oceanic and atmospheric components during initialization, the coupled system is not well balanced initially and may experience a shock when the forecast starts. Further, the imbalances between the mean states of the oceanic initial conditions and the coupled model contribute to systematic error of the forecast fields [Leetmaa and Ji, 1996]. In the study by Chen et al. [1995], initial conditions for the Cane and Zebiak [1985] model are generated in a self-consistent manner using a coupled data assimilation procedure. Initial conditions for each forecast are obtained by running the coupled model for the period from January 1964 up to the forecast starting time. At each time step prior to the forecast a simple data assimilation procedure is used whereby the coupled model wind stress anomalies are nudged toward the FSU wind stress observations. In this manner the coupled model itself is used to dynamically filter the initial conditions. Initialization shocks are reduced by providing a better balanced set of ocean-atmosphere initial conditions for the coupled forecast. Previously, the ocean initial conditions contained considerable high-frequency energy when forced by the FSU wind stress anomalies. The influence of the coupled model in the new initialization preferentially selects the low-frequency, interannual variability. This approach also results in a shallower thermocline in the western equatorial Pacific during most ENSO warm events with important implications for improved forecasts of warm event termination. Moreover, the coupled approach to initialization eliminates the springtime barrier to prediction that characterizes most coupled forecast schemes.
Recently, decadal-scale variability in the forecast skill has been noted in coupled models. Chen et al. [1995], for example, found that for the period 1982–1992, forecast skill was generally high for lead times of 12–24 months. Conversely, for the period 1972–1981, forecast skill was generally low for lead times longer than a few months. Balmaseda et al. [1995] also found generally higher predictability in the 1980s compared to the 1970s, and Goddard and Graham [1997] described reduced predictability associated with the 1993 and 1994–1995 El Niños relative to El Niños during 1982–1992. ENSO variations in the 1980s were generally stronger than those during the 1970s or during 1993–1995, suggesting that stronger ENSO events may be easier to predict than weaker events. It is also likely that the present generation of prediction models does not adequately represent the full range of physical processes responsible for the ENSO cycle or the interaction of ENSO with decadal time scale variations. These limitations could contribute to decadal fluctuations in predictability as well.
Although most data assimilation efforts in support of coupled models have focused on improving initial conditions, data assimilation techniques such as the Kalman filter have also been used as a means of parameter estimation in simple coupled models. In idealized versions of intermediate coupled models, there exist key parameters that govern the coupling strength between SST and the surface winds and the relation between the depth of the thermocline and the temperature of the water entrained into the ocean mixed layer. The particular values of these coefficients tend to determine the behavior of the coupled mode characteristic of the system. Similar to the way in which assimilation techniques have been used to estimate parameters such as the phase speed in shallow water models, the work of Hao and Ghil [1994] demonstrated how subsurface thermal data from the TAO array could be assimilated into coupled models to guide the proper estimation of key model parameters.
The preceding sections have described the evolution of the TOGA observing system and how it has contributed to scientific progress in studies of short-term climate variability during the TOGA decade. Development of this observing system was a major technological achievement, which revolutionized climate monitoring programs by stimulating increased demand for real-time ocean data delivery. The data from this observing system were essential to fostering advances in many aspects of TOGA research, including the following: (1) documentation of the ENSO cycle and related phenomena, such as the mean seasonal cycle and intraseasonal variability, with unparalleled resolution and accuracy; (2) testing of ENSO theories, such as the delayed oscillator; (3) development of new theoretical concepts relating to ocean-atmosphere interactions on seasonal-to-interannual timescales; (4) development of oceanic, atmospheric, and coupled ocean-atmosphere models; and (5) development of ocean data assimilation systems for improved climate analyses and for initializing climate prediction models. In short, measured against the goals of TOGA stated in section 1, the TOGA observing system was a tremendous success.
It is fortuitous that TOGA spanned a decade in which there was both a large swing from El Niño to La Niña conditions (1986–1989) and a period of prolonged anomalous warming (1991–1995). The dramatic change from El Niño to La Niña during the first half of TOGA heightened awareness about the importance of the cold phase of the ENSO cycle [e.g., Trenberth and Branstator, 1992; Halpert and Ropelewski, 1992] and afforded the opportunity to examine sharp contrasts between extreme climatic conditions in the Pacific and their impacts worldwide [e.g., Palmer et al., 1992]. On the other hand, the period 1991–1995 was unprecedented when viewed in the context of modern instrumental records dating back to the last century. The warm conditions evident during 1991–1995 have been interpreted as a single warm phase ENSO event, in which case it would be the longest in the past 100 years [Trenberth and Hoar, 1996]. An alternative interpretation is that 1991–1995 was characterized by three distinct warm events [Goddard and Graham, 1997], implying a recurrence rate significantly higher than the average 3-4 years expected from historical records. Either interpretation identifies 1991–1995 as unique in the modern record.
It is interesting to compare the evolution of warm events in Plate 1 with the Rasmusson and Carpenter [1982] composite, which was based on El Niño events from the 1950s to the 1970s. Rasmusson and Carpenter [1982] suggested that anomalous surface warming occurs first off the South American coast, peaking in March–May, then progresses westward along the equator into the interior basin, reaching a "mature phase" in December–February. Subsequently, warm SST anomalies and associated westerly wind anomalies weaken and eventually disappear by the following May. There were features common among the El Niño events observed during TOGA, such as anomalous warming in the equatorial cold tongue and large-scale weakening of the trade winds in the central and western Pacific. However, like the 1982–1983 El Niño prior to TOGA, none of these warm events evolved strictly according to the canonical Rasmusson and Carpenter [1982] composite.
Significant differences in duration, phasing, and spatial warming patterns observed during events of the 1980s and early 1990s defy easy categorization. Most pronounced warmings in the eastern and central Pacific in the 1990s, for example, occurred in boreal winter 1991–1992, boreal spring 1993, and boreal fall 1994. This disparate timing of maximum warm anomalies raises questions about the dynamical links between the seasonal cycle and the evolution of El Niño. Moreover, South American coastal warming did not generally precede maximum SST anomalies in the equatorial cold tongue, as in the Rasmusson and Carpenter [1982] composite. Deser and Wallace [1987] had earlier found that coastal warmings appear to be only loosely coupled to the broader basin-scale manifestations of El Niño, a result that appears also to apply to warm events observed during the TOGA decade. Also, considering the 1993 and 1994–1995 warmings as separate events, their duration was significantly shorter than the norm of 12–18 months for El Niños of the past.
Consistent with the complexity of the observed interannual variability, tests of ENSO theories using data prior to and during the TOGA decade suggest that more than one set of mechanisms can give rise to ENSO timescale warm and cold events in the tropical Pacific. The delayed oscillator theory, for example, can often, but not always, be invoked to explain the termination of ENSO warm events. On the other hand, delayed oscillator physics cannot generally account for the onset of warm ENSO events. New physical hypotheses are being formulated regarding the ENSO cycle, based on the failure of existing theories to explain the full range of observed variability.
The unusual warm conditions prevailing near the date line in the equatorial Pacific during 1991–1995 raise questions about the relationship between the ENSO cycle and decadal timescale variability. The persistent warm anomalies are the reflection of a decadal timescale variation that has higher latitude manifestations in North and South Pacific SSTs [e.g., Latif et al., 1997; Wallace et al., this issue; Zhang et al., 1997]. This decadal mode may result from decadal modulations in the intensity and/or frequency of ENSO events, or it may be a mode of coupled ocean-atmosphere variability with dynamics distinctly different from those of ENSO. In either case the decadal timescale of this variation and its manifestations at higher latitudes suggest a link to decadal timescale processes that maintain the equatorial thermocline [Fine et al., 1987; McPhaden and Fine, 1988]. These processes involve the ocean thermohaline circulation which couples the tropical ocean to the subtropical and higher-latitude North and South Pacific Ocean [e.g., McCreary and Lu, 1994; Lu and McCreary, 1995]. Decadal timescale variations in the overlying atmospheric circulation at midlatitudes [Trenberth and Hurrell, 1994; Latif and Barnett, 1995; Zhang et al., 1997] alter patterns of air-sea heat exchange, providing a mechanism by which the formation of thermocline water masses can be affected in density surface outcrop regions [Miller et al., 1994]. A theory for self-sustaining decadal time scale oscillations involving ocean-atmosphere interactions and heat transports between the tropical and extra-tropical oceans has been proposed recently by Gu and Philander [1997].
Observed variability during TOGA also suggests a possible connection between El Niño and global warming. Average SSTs in the tropical Pacific were unusually high during the 1980s and 1990s, at the same time that there was a trend for warmer global surface air temperature. The tropical Pacific SSTs were warmer because of a greater intensity, frequency, and/or duration of warm ENSO events. Two recent studies [Kumar et al., 1994; Graham, 1995] based on atmospheric model simulations forced with observed SSTs for the 1980s and 1990s suggested that the warming of global surface air temperature for this period may have been induced by the warming of SST in the tropical Pacific. Tropical Pacific SSTs in these simulations were prescribed from observations, however. It is possible that the character of ENSO changed and that SSTs were warmer because of anthropogenic greenhouse gas warming [Trenberth and Hoar, 1996]. There is no consensus on this issue, and recently, Cane et al. [1997] argued that global warming should lead to a cooling of the tropical Pacific. Clearly, resolution of the questions concerning ENSO, decadal variability, and anthropogenic greenhouse gas warming will require considerably more research.
TOGA demonstrated the synergy that can emerge from the combined use of data and dynamical models. As a measure of progress, prior to TOGA, there was no system of routine data assimilation for tropical ocean climate analyses and no routine short-term climate prediction efforts. However, during TOGA, models were used to help design the observing system, and data from the observing system were then used to foster model development and to initialize models for short-term climate prediction. Now many ENSO prediction modeling groups have been established [National Weather Service, 1997], and prediction models, initialized with TOGA data sets, show significant skill for lead times of up to 1 year. The skill of these predictions is likely to improve as we learn more about the underlying dynamical processes involved in ENSO and as models and assimilation systems improve.
TOGA also demonstrated the synergy that can emerge from the combined analysis of satellite and in situ measurements. In situ measurement systems provide high-accuracy information on both surface and subsurface ocean variability, the latter of which is not directly accessible to satellites. In situ measurement systems also provide necessary data for ongoing calibration and validation of satellite retrievals. The strength of the satellite data, on the other hand, is their near-global coverage and uniform time-space sampling characteristics. Unfortunately, the full potential for satellite missions for climate research during TOGA was not realized in part because most of the satellite missions were sponsored for reasons other than climate research and some (like TOPEX/POSEIDON) were originally intended as one-time experimental missions. Similarly, the launch of NSCAT was so often delayed that eventually it fell outside the TOGA time frame. Coordination between agencies and countries sponsoring satellite missions did not always succeed because of uncertainties in funding, payload development, and launch dates. This lack of coordination led to a 2-year gap in altimeter measurements between the U.S. Navy Geosat mission and the ERS-1 mission. Nonetheless, the tremendous value of those satellite data that were acquired during TOGA bodes well for the future application of satellite measurements to ocean climate studies.
As a result of TOGA, we are now entering a new era of climate research and forecasting. The World Climate Research Program (WCRP) has embarked on a 15-year (1995–2010) study of Climate Variability and Predictability (CLIVAR), one element of which, the Global Ocean-Atmosphere-Land Studies (GOALS) program focuses on seasonal-to-interannual variability [National Research Council, 1994b; World Climate Research Program, 1995b]. Also, a newly instituted International Research Institute for Climate Prediction (IRICP) will begin to issue routine short-term ENSO forecasts, conduct research on ways to improve those forecasts, and help to coordinate the use of the forecast products for various socioeconomic applications [International Research Institute for Climate Prediction Task Group, 1992]. Likewise, some national meteorological centers are already routinely issuing climate forecasts [e.g., National Centers for Environmental Prediction, 1996], and others intend to do so in the near future.
The success of these research and forecasting activities requires that essential elements of the TOGA observing system be continued for the foreseeable future. Explicit guidance on the development of post-TOGA climate observing systems is contained in the reports of various planning committees that have considered the observational needs of future climate programs [e.g., National Research Council, 1994b; Ocean Observing System Development Panel, 1995]. These reports are unanimous in their recommendations to continue the observing system developed under TOGA in support of short-term climate prediction. For some components of the observing system this may require transfer of the responsibility for long-term, systematic measurements from the research community to the operational oceanographic and/or meteorological communities. Effecting this transition will be challenging because there is no precedent for institutionalizing an observing system built entirely within the framework of a climate research program.
The need for long-term support of critical climate measurements has motivated planning for the Global Climate Observing System (GCOS) as well as the climate module of the Global Ocean Observing System (GOOS). These emerging international programs, modeled loosely on the World Weather Watch for weather forecasting, are intended to foster and coordinate measurements for a wide range of climate applications. As national commitments were essential in developing the TOGA observing system, so will they be essential in maintaining the observing system after TOGA. GOOS and GCOS are at different stages of evolution in different countries involved in supporting climate observations, complicating coordination at the international level. However, CLIVAR and GCOS/GOOS have recognized the merits of collaboration to ensure that an effective post-TOGA observing system is maintained. Therefore, in the near term, it is almost inevitable that the post-TOGA observing system will be maintained under a mix of research and operational support.
In the meantime it is of paramount importance that the existing data stream not be interrupted. Tremendous effort was expended in developing an adequate infrastructure to support the collection of critical data sets during TOGA. This infrastructure, involving cooperative relationships between research institutions and government agencies in several countries, was established through painstaking evaluation and oversight by the international scientific community over the course of 10 years. This infrastructure is fragile; premature curtailment or disruption of observational efforts could have disastrous and long-lived effects on the development of future climate observing systems. Thus a conservative approach must be adopted in recommending changes to either observational strategies or to the organizational framework in which the observations are supported. Conservatism does not imply that the observing systems for post-TOGA climate studies should be static in their design, though. On the contrary, the observing system should be flexible enough to take advantage of new advances in technology. Likewise, it is essential that there be ongoing assessments of the observing system design and that these assessments be guided by scientific priorities.
Much of this paper has dealt with the TOGA observing system in the tropical Pacific, where TOGA focused its effort as a first priority. Clearly, adequately observing the tropical Pacific was a sine qua non for making progress on understanding and predicting ENSO. In contrast, scientific questions relating to the climatic impacts of ocean-atmosphere interactions were not as thoroughly explored in the other two ocean basins, and resources were too limited to allow for uniform development of observing system components throughout the global tropics during the TOGA decade. Nonetheless, as a consequence of TOGA, our understanding of ocean-atmosphere interactions in the Indian and Atlantic Oceans has significantly improved. New hypotheses have emerged, such as the role of the Indian and east Asian monsoons in ENSO [e.g., Webster and Yang, 1992] and the role of both Pacific and Atlantic SST variations in affecting climate in the Atlantic basin [e.g., Servain, 1991; Zebiak, 1993; Delecluse et al., 1994]. Also, while there is ongoing debate about the origin of ENSO-related SST anomalies in the North Pacific and their effects on climate variability over North America [e.g., Lau and Nath, 1994], even stronger decadal timescale variations in North Pacific SSTs have recently been documented [e.g., Zhang et al., 1997]. The relationship of these decadal variations to ENSO and to global climate variability, in general, needs to be better understood. Thus geographic expansion of in situ observational efforts should be carefully considered as part of the post-TOGA climate research agenda.
The need for an improved climate observing system was underscored during the planning stages of TOGA in the early 1980s, when the scientific community was caught completely off guard by the 1982–1983 El Niño, the strongest in over a hundred years. This El Niño was neither predicted nor even detected until several months after it had started. At the time, most in situ oceanographic data were available for analysis only months, or in some cases years, after they had been collected. So only a handful of scattered reports from islands and volunteer observing ships were available to track conditions in the equatorial Pacific in real time (delay of less than a day) or near-real time (delay of less than a month). Some SST reports were extraordinarily high and suggestive that an El Niño event might be underway. However, they were discounted as erroneous for several reasons. One reason was that there had been no "buildup" of sea level in the western Pacific by stronger than normal trade winds prior to 1982, presumed to be a necessary precursor of El Niño [Wyrtki, 1975]. Also, there had been no warming off the west coast of South America in early 1982, considered to be part of the normal sequence of events characterizing the evolution of El Niño [Rasmusson and Carpenter, 1982].
To complicate matters, in situ data were rejected from blended satellite/in situ SST analyses produced operationally by the U.S. National Centers for Environmental Prediction (NCEP), then known as the National Meteorological Center (NMC). These analyses indicated that the equatorial Pacific SSTs were near normal, or even slightly colder than normal, during much of 1982. However, the effect of the March–April 1982 eruptions of the Mexican volcano El Chichon on satellite SST retrievals was not fully appreciated at the time. These eruptions injected a cloud of aerosols into the lower stratosphere, where prevailing winds spread it around the globe at low latitudes within 3 weeks. The aerosols, whose effects were not included in algorithms to convert observed satellite radiances to SSTs, led to cold biases of several degrees centigrade in the satellite SST retrievals. Cloud detection algorithms interpreted these retrievals as cloud contaminated and replaced them with climatological mean SSTs. In situ data were then rejected because they differed so greatly from the satellite analyses, which were strongly biased toward climatology. It was only after reports from the R/V Conrad in September–October 1982 that the thermocline in the eastern equatorial Pacific was 50–100 m deeper than normal [Toole and Borges, 1984] that the scientific community realized to what extent existing data sources had misinformed and misled them and likewise how misguided was the notion of a "canonical" El Niño with a fixed pattern of stages from event to event.
The history of moored measurements for climate studies in the equatorial Pacific dates back to the 1970s, when surface current meter moorings were first deployed along the equator as part of the EPOCS program [Halpern, 1987b] and the NORPAX Hawaii-Tahiti Shuttle [Wyrtki et al., 1981; Knox and Halpern, 1982]. Based in part on these early successes, original plans in TOGA called for a small number of moorings to be deployed near the equator and in gaps between widely spaced XBT lines [U.S. TOGA Office, 1988].
However, the 1982–1983 El Niño highlighted the inadequacy of existing ocean observational networks for climate studies, in part because of the lack of high-quality real-time data by which to monitor evolving conditions in the tropical Pacific Ocean. This realization spurred attempts to develop telemetry systems for deep ocean moorings at NOAA's Pacific Marine Environmental Laboratory. The most notable development in this regard was the Autonomous Temperature Line Acquisition System (ATLAS) mooring [Milburn and McLain, 1986; Hayes et al., 1991a], which incorporated many proven design concepts from taut-line current meter moorings used in earlier equatorial ocean studies [Halpern, 1996]. However, significant cost savings were achieved by eliminating current meters from the suite of instrumentation and by targeting temperature rather than velocity as the primary oceanographic variable. Elimination of current meters, whose moving parts (rotors, vanes, or propellers) were sensitive to mechanical wear and biofouling in the energetic and biologically productive upper layers of the equatorial Pacific, also extended the expected lifetime of the mooring from 6 months to 12 months. Equally significant, the ATLAS mooring was designed to telemeter air temperature, SST, and subsurface temperature data to shore in real time via Service Argos. In 1986, real-time winds were added to the ATLAS system, adapting earlier design concepts developed for real-time wind measurements from current meter moorings [Halpern et al., 1984]. Relative humidity sensors were added to ATLAS moorings in 1989.
ATLAS sampling and data transmission schemes have evolved with time. The current generation ATLAS telemeters all data as daily averages and, in addition, as hourly values for SST and surface meteorology coincident with three to four satellite overpasses per day. Data are also internally recorded and available upon recovery of the mooring system. A recent assessment of instrumental accuracies indicates errors of about 0.03°C for SST, 0.2°C for air temperature, < 0.1°C for subsurface temperature, 0.2 m s-1 for wind speed, and 4% for relative humidity [Mangum et al., 1994; Freitag et al., 1995]. The estimate of wind speed error (unlike the other estimates) does not take into account possible calibration drift for instruments deployed at sea for up to one year. An assessment of this drift is presently underway, and preliminary results suggest that including it may lead to an overall accuracy of about 0.5 m s-1 for wind speed.
The early technical successes of the ATLAS mooring program and the recognized value of the data for short-term climate studies led to multinational plans for a basin-scale expansion of the array during the second half of TOGA [National Research Council, 1990]. This expansion was feasible because the relatively low cost of the ATLAS mooring allowed for its deployment in large numbers and because the 1-year ATLAS design lifetime made for manageable long-term maintenance costs and ship time requirements. The array, dubbed TOGA-TAO [Hayes et al., 1991a], far exceeded in scope what had been originally anticipated as a moored buoy component of the TOGA observing system [U.S. TOGA Office, 1988].
Coordinated with the early ATLAS mooring program, but separate from it, was a parallel effort to develop a long-term array of current meter moorings for TOGA studies in the Pacific [World Climate Research Program, 1990a]. These moorings were concentrated on the equator where direct measurements would be most valuable in view of the limited applicability of the geostrophic approximation. Siting was based in part on historical precedent (i.e., where long records already existed) and the need to sample different hydrodynamic regimes (e.g., cold tongue, warm pool). It became apparent, however, as the ATLAS program expanded, that the current meter mooring and ATLAS mooring programs should be integrated more fully for a variety of technical, logistic, and scientific reasons. Thus, during the second half of TOGA, TAO was configured to include both ATLAS and current meter moorings in a single unified mooring program [McPhaden, 1993a]. Details of current meter mooring design, sampling characteristics, and instrumental accuracies can be found in work by Halpern [1987a, c], McPhaden et al. [1990b], McCarty and McPhaden [1993], Lien et al. [1994], Freitag et al. [1995], Plimpton et al. [1995], and Weisberg and Hayes [1995].
Design criteria for the TAO array were based on general circulation model simulations of wind-forced oceanic variability and on empirical studies of space-time correlation scales as described in section 2. The array was built up over time and maintained through a series of research cruises at roughly 6-month intervals. These cruises were necessary to deploy new mooring systems and recover old mooring systems that were close to or past their design lifetimes. The array was completed at the very end of TOGA in December 1994, with deployment of an ATLAS mooring at 8°N, 156°E [McPhaden, 1995].
A subset of the real-time TAO data stream, formatted by Service Argos into World Meteorological Organization (WMO) code, is retransmitted on the GTS. The data are then available to operational meteorological and oceanographic centers around the world. The availability of TAO data on the GTS increased significantly in November 1992 after long-standing problems with the Argos-GTS link were finally resolved; data throughput increased at that time from 10–30% to 80–90% [McPhaden, 1993b].
The rapid growth of the TAO array during the second half of TOGA has led to improvements in the quality of several important operational climate analysis and prediction products. For example, at present approximately half the wind observations used in FSU monthly Pacific wind analyses in the band 10°N–10°S are from TAO buoys (Figure B1). TAO data are also included in the weekly NCEP SST analysis (see section C1). The Comprehensive Ocean Atmosphere Data Set (COADS) [Woodruff et al., 1987], a global compilation of marine observations since 1854, also incorporates TAO data. As of this writing, only those TAO data available from the GTS have been included in COADS. A COADS reanalysis of data collected after 1980, including a more comprehensive set of delayed-mode TAO data, is planned for the near future (S. Worley, personal communication, 1996).
Figure B1: GTS ship (small solid dot) and buoy (open circles) wind reports used in the Florida State University Pacific surface wind analysis for the month of December 1994. In the latitude band 10°N–10°S a total of 6970 observations were reported; 3809 of these reports (55%) were from TAO buoys (data courtesy of D. Legler, 1997).
Development of the TAO array required an extraordinary effort from individuals and institutions in several countries, at the core of which was sustained support provided by the United States, Japan, France, Taiwan, and Korea. As one measure of effort, accumulated over the 10 years between 1985 and 1994, more than 400 TAO moorings were deployed on 83 research cruises involving 17 ships from six different countries, requiring a total of 5.7 years of shiptime. At present, nearly 1 year of dedicated shiptime per calendar year is required to maintain the fully implemented array of nearly 70 moorings. Overall, data return has been > 80%, with many sites providing over 90% data return. Regions of data return < 80% are found in the far eastern and western Pacific, where vandalism by fishing fleets has been an ongoing problem [e.g., Koehn et al., 1995, 1996]. Scientific use of TAO data has been encouraged by the development of sophisticated data management, display, and dissemination capabilities. These include the TAO workstation and access to the data via anonymous file transfer protocols and the World Wide Web [Soreide et al., 1996].
In the early 1970s the Argos Doppler ranging system became operational on National Oceanic and Atmospheric Administration (NOAA) polar orbiting weather satellites, and a cost-effective technique of listening to and locating radio transmitters on the global ocean surface was made available to oceanographers. This spawned the design and construction of a large number of ocean surface drifters, both for measuring ocean circulation as well as for use as platforms for deploying a variety of meteorological sensors. Throughout the 1970s, typical drifter configurations consisted of a 100–200-kg aluminum surface float and a World War II surplus parachute or 2- × 6-m rectangular window-shade drogue attached with rope and chain to a depth of 10–30 m. Over 150 of these drifters were released into the Gulf Stream system [Richardson, 1983], and the largest array deployment was in the Antarctic Circumpolar Current, where about 180 drifters were operational during the intensive observation phase of the Global Atmospheric Research Program (GARP) First Global GARP Experiment (FGGE) in 1979–1980 [Hofmann, 1985]. Small arrays of FGGE drifters with drogues were also deployed in the tropical Pacific as part of the EPOCS program between 1979 and 1987, with the main purpose of understanding eastern tropical circulation.
During the planning phase of TOGA it became clear that accurate global fields of SST, atmospheric pressure and ocean basin-wide patterns of surface circulation were required [World Climate Research Program, 1985] (see also Table 1). A potentially valuable tool was the Argos-tracked drifter, but several serious questions arose regarding the feasibility of designing an affordable instrument that could be deployed in global arrays. The drifters used during FGGE were too heavy to be routinely deployed from merchant ships or by air; they were very costly to build and did not retain their drogues longer than several months. No mechanical design improvements had been made to them since 1975. There were no engineering standards or field-verified hydrodynamic models by which to design a Lagrangian drifter in order that its water-following capability could be determined to the accuracy required by TOGA. Finally, the tariffs charged by Service Argos, the firm which had the exclusive right to decode Argos location data, would severely limit the extent of a global, long-term deployment. To meet TOGA objectives, a two-pronged program of drifter deployments was developed, as described below.
In 1982 a group of oceanographers and engineers met at the National Center for Atmospheric Research to consider the challenges presented by the WCRP requirements for global ocean and atmosphere monitoring and to determine how a variety of newly designed ocean Lagrangian tools could be used to meet these needs. It was decided that a low-cost, lightweight surface drifter should be developed. Funding for the new drifter development came first from the Office of Naval Research and then from NOAA and the National Science Foundation.
By 1985, competing drifter designs had emerged from the Draper Laboratory, NOAA/Atlantic Oceanographic and Meteorological Laboratory (AOML), and Scripps Institution of Oceanography. The field measurements of the water-following capability of the drifters, with vector-measuring current meters attached to the top and bottom of the drogue, were done over the period of 1985–1989 [Niiler et al., 1987, 1995]. Several modeling studies of drifter behavior in steady upper layer shear and linear gravity wave fields were also done [Chabbra et al., 1987; Chereskin et al., 1989]. These studies provided a rational basis for the interpretation of the drogue slip measurements in the field. A TOGA/WOCE Surface Velocity Program (SVP) was organized to seek broad international support for drifter acquisitions and deployments.
By 1986 several SVP drifter designs had emerged and were being used in research programs in the Atlantic and Pacific. In 1988 a Pacific basin-wide TOGA process study, the Pan-Pacific Surface Current Study [World Climate Research Program, 1988], became operational. Its technical objectives were to use VOS ships to maintain an array of 120 drifters for a 3-year period and to select from the competing SVP drifter designs the most robust elements. Its scientific objectives were to obtain a tropical Pacific basin-wide field of surface currents and SST for the purpose of studying a variety of processes that determine SST evolution. Barometers were added to the SVP drifters in 1991, and in 1992, salinity sensors became an operational system on drifters in TOGA COARE. SVP drifters were deployed for WOCE in significant numbers in the Pacific by 1992, in the Atlantic as part of the Atlantic Climate Change Program in 1992, and in the Southern and Indian Oceans in 1994. By the end of TOGA, over 700 drifters were operational, and SVP emerged as the Global Drifter Program, maintained by resources from 16 countries.
The evolution of the SVP drifter to the Global Lagrangian Drifter took nearly 5 years of design and evaluation. It now consists of a spherical surface float that carries the electronics, SST, barometer, and drogue-on sensors. This float is tethered with plastic-coated wire to a holey sock drogue centered at 15-m depth [Sybrandy and Niiler, 1991; Sybrandy et al., 1995]. In the subtropical oceans the mean lifetime of a buoy (defined in terms of drogue retention) is 440 days; in the Southern Ocean the mean lifetime is 280 days. The accuracy of the water-following capability is dependent upon the winds and the "drag area ratio," the ratio of the frontal drag areas of the drogue relative to the surface float and tether [Niiler et al., 1995]. These drifters were designed to slip < 1 cm s-1 in 10-m s-1 winds and have a drag area ratio about 5 times larger than was used in FGGE drifters [Niiler and Paduan, 1995]. At the time of deployment the calibrated accuracy of the SST sensor is 0.1°C, and the accuracy of the barometer is 1 mbar. Location data provided by Service Argos have a minimum error of 300 m. To reduce Service Argos fees, these drifters transmit one third of the time in a 24- or 72-hour period.
Service Argos processes these data for location, SST, and sea level pressure and places it on GTS within 2 hours of reception. The GTS data are quality controlled and used on an operational basis by the meteorological agencies for weather and climate prediction and in a variety of data products that assess the nature of the variability of the oceans and lower atmosphere. For example, NCEP uses the raw drifter barometer data in real time off the west coast of the United States to aid in marine weather broadcasts and forecasts. Scientific quality data are processed at the Global Drifter Center at NOAA/AOML, and on a 6-month interval, they are deposited at Marine Environmental Data Service (MEDS), Canada, for release to the scientific and operational communities.
In TOGA the SVP drifters were deployed from research vessels, VOS, and airplanes. The average failure rate upon ship deployment was 5% and from airplanes 15%. In the tropical Pacific most of the drifters were released near the equator. The objective was to maintain drifter arrays with enough samples in 2° latitude × 8° longitude areas to define the 15-m circulation. The sample size (Figure B2) depends more on the nature of the deformation field of the circulation than upon where drifters were released. For example, there were many more deployments in the eastern Pacific equatorial waveguide than in the North Equatorial Countercurrent, although the data density was much larger in the latter because of the nature of the surface flow and its variability.
Figure B2: Number of 5-day observations of velocity observed in 2° latitude × 8° longitude areas from surface drifters between January 1, 1979, and December 31, 1995, in the tropical Pacific. The total number of 5-day observations is 81,589. The maximum number of 5-day observations possible in any given box is 1098.
While the SVP drifter was being developed, the second part of the two-pronged program for drifter deployment was getting underway. The U.S. TOGA Scientific Steering Group in 1983 authorized a program to begin deployment of FGGE-type drifters in the Southern Oceans, managed by NOAA's National Ocean Service and National Data Buoy Center. These drifters carried barometers and SST sensors inside the metal hulls, and the data were reported routinely via Argos through the GTS as an operational system. Some drifters had a long rope or cable attached to the base, while others drifted freely in the wind and waves. In 1984, about 40 FGGE-type drifters were deployed, but escalating costs, inflation, a noncompetitive environment for industrial construction, and fixed budgets reduced the array to 20 drifters by 1994. Several operational meteorological agencies contributed drifters to this Southern Ocean FGGE drifter program through the Drifting Buoy Cooperation Panel (which later became the Data Buoy Cooperation Panel). The data reported on GTS is stored in MEDS, Canada.
TOGA inherited a substantial Pacific tide gauge network that was largely installed during NORPAX. Recognition of the importance of the El Niño phenomenon and many of the early diagnostic studies of it may not have been possible without the sea level data. For example, the sea level changes associated with the El Niño events of 1972, 1976, and 1982–1983 were described prior to the beginning of TOGA in a series of papers by Wyrtki [1975, 1977, 1979, 1984, 1985b].
Efforts in the Pacific during TOGA were focused on expanding and refining this network. As the network was expanded, new gauges were generally placed at least 500 km from existing ones. In the Indian and Atlantic Oceans, however, few gauges existed or were reporting data regularly at the start of TOGA. Hence significant effort was undertaken to remedy this situation. At present the Indian Ocean network is nearly complete, in the sense that most of the available sites have been instrumented. The network in the Atlantic Ocean, on the other hand, remains limited by the scarcity of islands suitable for gauges. Early in TOGA, it was determined that the problem in the Atlantic was basically one of collecting available data, rather than attempting to place new instruments. This data collection effort was also largely successful, with 21 sites reporting data by the end of 1994 (Table 3).
The University of Hawaii Sea Level Center was responsible for coordinating, maintaining, and expanding the tide gauge network in the tropical regions for TOGA purposes. Instrumentation used in the network consists of a heterogenous blend of instruments ranging from bubbler-type pressure gauges to state-of-the-art acoustic gauges, as described by Carter et al. [1987]. The majority of the sites, however, have traditional float gauges in stilling wells. Some general information on the instrumentation available for sea level measurements is given by Pugh [1987], and more specific information about the equipment used by the University of Hawaii Sea Level Center can be found in work by Kilonsky and Caldwell [1991] and Mitchum et al. [1994].
The heterogeneity of the instrumentation is due in part to the logistics involved in maintaining gauges over a wide geographical area. Simple bubbler gauges are favored at very remote locations, whereas sophisticated acoustic gauges have been installed at several readily accessible sites. At most sites, however, the float-type gauge is favored because of its relatively low cost, which allows the placement of redundant systems at each site. This philosophy has been proven successful, in that the University of Hawaii Sea Level Center network typically has a data return exceeding 97%, even with maintenance trips spaced at 2–3-year intervals.
The redundant nature of the University of Hawaii Sea Level Center installations allows an estimate of the instrumental accuracy of the float-type gauges. There are typically two independent stilling wells with completely separate instrumentation at each site, and these wells are within 1–2 m of one another. Differences between the time series are taken to be an estimate of the instrumental accuracy. These intercomparisons show that for timescales longer than 2 days the redundant float-type gauges agree to ~0.5 cm. Bubbler gauges are typically noisier, with differences of the order of 2 cm. Frequency spectra of the differences show that the noise is approximately white and will thus be negligible on monthly mean timescales.
A more significant concern is possible contamination of the tide gauge time series by local island effects distorting the large-scale open ocean pressure field. This type of error is more difficult to estimate, but recent intercomparisons with sea surface heights from satellite altimeters suggest that it is not a very significant error source at low frequencies. Mitchum [1994] and Cheney et al. [1994] have shown that the sea levels from the tide gauges agree with the heights from the TOPEX altimeter to ~4 cm for timescales longer than 20 days and to 2 cm for timescales longer than 2 months. These estimates are comparable to what is expected from the error budget for the altimeter alone, which implies that the tide gauges cannot be contributing a large amount of variance to the differences.
For the stations in that portion of the TOGA tide gauge network maintained directly by the University of Hawaii Sea Level Center, data are returned for many stations via the data channels on the geostationary satellites, and this real-time delivery is backed up by delayed transmission of tapes from the stations to the Sea Level Center on a monthly basis. For stations using only the delayed mode data delivery, data are processed and available to the community within several months of collection. Many of the TOGA tide gauges contribute to the operational data flow handled by the IGOSS Sea Level Project in the Pacific and to the near-real-time data set provided by the WOCE "Fast Delivery" Sea Level Center, both of which are also operated by the University of Hawaii Sea Level Center.
The international system of voluntary observation ships, initiated in the last century [Maury, 1859], is still a critical element of modern meteorological and oceanographic observation networks. This section treats different components of the VOS program separately. Surface marine meteorological data are reviewed first (section B4.1), followed by a discussion of the VOS XBT program, which was one of the major observational initiatives of TOGA (section B4.2). For completeness we also provide a brief discussion of the VOS sea surface salinity effort in the Pacific (section B4.3).
There are currently around 7000 VOS worldwide, operated by about 50 countries. They collect observations on sea surface pressure, wind velocity, sea state, humidity, and SST, as part of the World Weather Watch (WWW). Each month, typically, 100,000 or more surface observations are collected and transmitted in real time to national meteorological centers via satellite communication systems or via coastal radio stations. The meteorological centers are responsible for entering the data on the GTS for general use. VOS coverage is excellent in the vicinity of the well-traveled shipping routes (e.g., the North Pacific and North Atlantic) but has serious gaps in the southern oceans and in parts of the tropical oceans [Weller and Taylor, 1993].
Prior to the establishment of TAO and other dedicated TOGA observing systems, data from VOS marine reports and from island weather stations constituted the bulk of the available information on seasonal and interannual variability in tropical surface marine meteorological fields. The TOGA data requirements for surface fields and fluxes (Table 1) were based almost entirely on knowledge derived from analyses of VOS data [e.g., Taylor, 1984]. The International TOGA Project Office [1992] made several suggestions for improving the quality and density of VOS observations, but by and large, these were not implemented. Nonetheless, analyses of VOS data were extremely valuable for TOGA.
The creation of COADS [Woodruff et al., 1987] was a development based largely on VOS surface data that had a significant impact on climate research during TOGA. Prior to 1985, scientists who wished to work with the conventional surface marine data set often had to go through a laborious process of data extraction from the archives, followed by extensive quality control and analysis. COADS substantially reduced this impediment by creating a single data set of all available archived marine observations. The data were quality controlled and made widely available. This compilation was the basis for the Oberhuber [1988] and da Silva et al. [1994] climatologies and has been the basis for many recent studies of longer-term variability [e.g., Shriver and O'Brien, 1995].
Perhaps the most significant development in terms of the TOGA scientific history was the application of surface marine wind observations to produce time-varying winds. Wyrtki and Meyers [1975, 1976] produced the first such maps of wind and wind stress over the tropical Pacific Ocean, though on a coarse 2° latitude × 10° longitude grid. Esbensen and Kushnir [1981], Han and Lee [1983], and Hellerman and Rosenstein [1983] also exploited the marine data set to produce global analyses of wind stress and marine fields, but only for the seasonal and annual means. The Mesoscale Air-Sea Interaction Group at Florida State University (FSU), motivated by the need to produce a wind field data set suitable for forcing tropical ocean models, reanalyzed the Wyrtki and Meyers wind data [Goldenberg and O'Brien, 1981]. These analyses were for pseudostress (the product of the wind velocity times wind speed) and were originally restricted to the tropical Pacific Ocean (30°S–30°N) on a 2° × 2° grid. Focusing on pseudostress allowed Goldenberg and O'Brien [1981] to avoid complications due to uncertainties in specification of drag coefficients while at the same time including at least some of the nonlinearity of the wind stress formulation, which is quadratic in wind speed.
The FSU wind analysis evolved considerably through the period of TOGA [Legler and O'Brien, 1984; Legler, 1991; Stricherz et al., 1992]. Monthly analyses are now performed routinely in near-real time for the Pacific Ocean using data available from the GTS. The fact that these analyses have been made available in near-real time allowed the development of timely and useful prediction systems like that of Cane et al. [1986]. Recently, full development of the TAO array during the second half of TOGA has approximately doubled the number of wind estimates used in the FSU analyses between 10°N and 10°S in the equatorial Pacific (Figure B1). Yearly reanalyses are performed augmenting GTS data with delayed mode data from National Climate Data Center (NCDC) archives and COADS.
Legler et al. [1989] extended the FSU analysis system to the Indian Ocean using techniques that allow information from various platforms, including satellites, to be merged. This technique has been extended to include surface fluxes over the Indian Ocean for the period 1960–1989 [Jones et al., 1995]. Rao et al. [1991] also analyzed the COADS data for the tropical Indian Ocean region to produce a consistent set of heat flux fields. These fields have been used in various numerical models of the Indian Ocean [e.g., McCreary et al., 1993].
In the tropical Atlantic Ocean one of the first time-varying analyses of surface marine data was produced by the Institut Français de Recherche Scientifique pour le Développement en Coopération (ORSTOM) group at Brest, France, following the methodology developed by the FSU [Servain et al., 1984, 1985]. Also, Reverdin et al. [1991a] analyzed the wind stress between 20°S and 30°N in the tropical Atlantic, using merchant ship wind observations. These analyses have been used in several numerical modeling studies, including Blanke and Delecluse [1993] and Braconnot and Frankignoul [1994].
The accuracy of surface analyses based on merchant ship marine data is dependent on the quality and sampling density of the input data. For example, Weare [1989] cataloged a number of different systematic errors in surface marine observations, including conversion of Beaufort wind force observations to wind speeds and spurious warming in SSTs from engine intake temperatures. Systematic errors like these are significant and cannot be removed by increased sampling density, as can random errors. As an example of the magnitude of these effects, Weare [1989] also concluded that uncertainties in latent heat flux computed from VOS data exceeded 30 W m-2 everywhere. Cardone et al. [1990] also cautioned that differing interpretations of Beaufort wind observations in the historical data set can lead to artificial trends in surface analyses, such as that of Legler and O'Brien [1984].
Major events in the evolution of XBT sampling since the instrument was invented were discussed by Meyers et al. [1991]. The XBT is a temperature profiler commonly dropped from VOS recruited from the merchant shipping, fishing, and military fleets [e.g., Baker, 1981; Sy, 1991]. The most commonly used models (T4 and T7) measure to a depth of 460 and 760 m. The instrument was developed during the 1960s and over the years has perhaps been more extensively used than any other single oceanographic instrument. Among its advantages are that the measurements can be carried out quickly, while the ship is underway, without in most cases having to reduce speed; operation of the instrument is easily learned by a new observer.
According to the manufacturer's specifications the temperature accuracy of the XBT is ±0.15°C. Some studies have shown that probe-to-probe thermistor temperature variability can be <±0.06°C at the 95% confidence level [Sy, 1991]. The measurement of relative, vertical temperature differences is also more accurate than the specifications [Roemmich and Cornuelle, 1987] so that small inversions and finestructure are detectable in the profile. The depth is estimated from a drop-rate equation using the time elapsed after the probe enters the water. It has been demonstrated, however, that temperature profiles made using the T4, T6, and T7 probes exhibit a systematic error with depth that is associated with an inadequate drop-rate equation supplied by the manufacturer [Hanawa et al., 1995]. After correction for the systematic error the depth accuracy is within the manufacturer's specifications (±2% of depth or ±5 m) in ~82% of XBT drops. Quality control of XBT data is a major task because the instrument malfunctions before reaching 250 m in about 15% of the probe launches. The modes of instrument failure have been carefully documented [Bailey et al., 1994] and distinguished from real temperature inversions and other structure so that a data quality expert can recognize and flag most faulty data in postcruise processing.
Design of the VOS XBT array for TOGA recognized the need to map large-scale variations in thermal structure to a known accuracy on a grid that would barely detect the smallest scales of interest. A strategy of low-density sampling was devised to provide broad-scale, widely dispersed coverage in areas that have routine merchant shipping on a monthly-to-quarterly cycle. Sampling error due to unresolved small-scale variability such as eddies, tropical instability waves, and internal waves is a source of geophysical noise. Many studies since the late 1970s have shown that the noise variance is about equal to the variance of the large-scale signals [Meyers et al., 1991; White, 1995; Kessler et al., 1996]. Maps of large-scale signals are produced using optimal interpolation (OI) as a filter to remove (or reduce) the smaller-scale variability. The mapping error variance after OI is typically 0.3 to 0.5 times the signal variance, in the areas that are best sampled. In dimensional units this translates to mapping errors of about 4–6 m in the depth of isotherms [Smith and Meyers, 1996].
Using the method of OI to design a sampling strategy required a prior knowledge of the statistical structure of the subsurface temperature field. Of particular importance are the so-called "decorrelation scales of variability," which represent the typical spatial and temporal extent in latitude, longitude, and time of the most energetic features. The scales for the tropical oceans were estimated [Meyers et al., 1991; Meyers and Phillips, 1992] by fitting a Gaussian curve to the covariance function of temperature variability estimated from observations. Recognizing that the scales show considerable regional differences as well as differences in depth and time, a uniform set of e-folding scales was recommended for application throughout the tropical oceans, 2° latitude × 15° longitude × 2 months. Maps of the temperature field were found to be rather insensitive to the exact value of the decorrelation scales in regions with good data coverage; however, mapping errors changed considerably with changes in the assumed scales.
On the basis of the above considerations the recommended low-density sampling strategy was prescribed as one XBT drop per 1.5° latitude × 7.5° longitude per month. Experience has shown that the recommended low-density sampling can be achieved in regions with good VOS coverage by dropping an XBT every 6 hours along the regular shipping tracks. A shortcoming of the VOS XBT network is that merchant shipping does not cover all areas of the global ocean, so that XBT sampling must be combined with other observations from in situ instruments or altimetric data to achieve global coverage.
In addition to the description of large-scale signals and initialization of ocean models the design of VOS XBT sampling for TOGA also recognized a need to observe seasonal-to-interannual variations of major geostrophic currents in the tropical oceans. A strategy of frequently repeated sampling was devised for a few transequatorial VOS lines in each ocean, with a recommended sample rate of three observations per decorrelation scale in latitude and time [Meyers et al., 1991]. The frequently repeated sampling rate can usually be achieved with 4-hour sampling on 18 voyages per year. Some noise due to spatial aliasing may be introduced into analyses of repeat transect data, if the ship tracks are spread out in a swath, but are treated as having been exactly repeated [McPhaden et al., 1988c]. In most cases this error is much smaller than the signals of interest along frequently traversed lines in the tropical Pacific. On some routes, XCTD data are also collected [Roemmich et al., 1994].
Since the 1980s most shipboard XBT systems have recorded data on a personal (desktop or laptop) computer. Real-time delivery is achieved for most installations by sending data to the GTS via Argos or geostationary satellites. Some data still are sent to the GTS by coastal radio stations. Upper Ocean Thermal Data Assembly Centers provide expert quality control of delayed mode data which are archived at the WOCE/TOGA Subsurface Data Center in Brest, France. Based in part on VOS XBT data collected during TOGA and WOCE, the annual and seasonal mean upper ocean thermal structure of the global ocean has been documented with the most comprehensive data set available in the World Ocean Atlas 1994 [Levitus and Boyer, 1994].
Salinity data collected as part of VOS programs have provided valuable insights into near-surface water mass variability and its relation to atmospheric forcing in the tropics. Though not among the highest-priority measurements during TOGA, surface salinity nonetheless exhibits strong seasonal-to-interannual timescale variations that are important to understand in the context of coupled ocean-atmosphere interactions associated with ENSO. For this reason and to present a complete picture of the overall VOS effort in TOGA we briefly discuss SSS measurements in this section.
The history of SSS measurements based on VOS networks dates at least back to the early 1950s in the Gulf of Guinea [Berrit, 1961]. On the basis of this early effort, VOS SSS networks were initiated by ORSTOM in the Pacific in 1969 and in the Atlantic and Indian Oceans in 1977 [see Donguy, 1994, and references therein]. SSS measurements are obtained from water samples bottled by ship officers about every 60 nautical miles and later analyzed on shore by laboratory salinometers. As compared with CTD measurements, the accuracy of bucket measurements is estimated to be of the order of 0.1–0.2 psu.
TOGA inherited a decade-long VOS SSS network in 1985, but because of various obstacles the bucket sampling rate decreased dramatically in 1994 to about 25% of the 1985 rate. From the second half of TOGA and during the COARE Enhanced Monitoring Period, efforts were focused on complementary arrays of thermosalinographs installed on board merchant ships [Henin and Grelet, 1996], on TAO moorings [McPhaden et al., 1990c; Koehn et al., 1996], and on drifting buoys [Swenson et al., 1991]. When deployed, the accuracy of temperature and conductivity sensors on these platforms results in an accuracy of about 0.02 psu in salinity. Owing to the disproportionate availability of surface to subsurface salinity measurements, most TOGA-related salinity studies concern SSS only.
Errors in the 1982 sea surface temperature (SST) analyses discussed in Appendix A led to improved analyses at the NCEP, formerly NMC (Figure C1). These analyses used both in situ and satellite data. The satellite observations are infrared measurements from the AVHRR on the NOAA polar orbiting satellites. These data were processes operationally by NOAA's Environmental Satellite, Data, and Information Service (NESDIS) until 1993, when the responbility for operational processing was transferred to the Naval Oceanographic Office of the U.S. Navy [May et al., 1998]. The satellite SST retrieval algorithms are "tuned" by regression against quality-controlled drifting buoy data using the multichannel SST technique of McClain et al. [1985] and Walton [1988]. This procedure converts the satellite measurement of the "skin" SST (roughly a millimeter in depth) to a buoy "bulk" SST (roughly at 0.5 m depth). The tuning is done when a new satellite becomes operational or when verification with the buoy data shows increasing errors. The algorithms are computed globally and are not a function of position or time. Although the AVHRR cannot retrieve SSTs in cloud-covered regions, the spatial coverage of satellite data is much more uniform than the coverage for in situ data. As an example, the distribution of AVHRR retrievals for the last week of TOGA is shown in Figure C1, where the number of daytime and nighttime observations has been averaged onto a 1° spatial grid. Day and night have been separated because the cloud detection algorithms are different for day and night.
Figure C1: Number of SST observations for the week of December 25–31. (top) Regions on a 1° grid where the number of daytime or nighttime AVHRR retrievals is three or more. (bottom) The distribution of ship, buoy, and simulated ice SSTs. In Figure C1 (bottom right) the moored buoys are indicated by a circle, the drifting buoys by a dot, and the ice by a plus.
In situ SST data used in the NCEP analyses are obtained from two different sources. The data source from 1990 to present consists of all ship and buoy observations available to NCEP on the GTS within 10 hours of observation time. Prior to 1990, the data were obtained from the COADS [Woodruff et al., 1987]. COADS adds additional delayed data to the GTS data. After a wait of several years the procedure can roughly double the number of in situ observations. The distribution of real-time in situ data for the last week of TOGA is shown in Figure C1. Figure C1 (top) shows the distribution of observations from ships. These observations are surface marine observations, which are roughly 20 times more frequent than XBT observations. This distribution depends on ship traffic and is most dense in the midlatitude northern hemisphere. Figure C1 (bottom) shows the in situ observations from drifting and moored buoys. The deployment of the buoys has partially been designed to fill in some areas with little ship data. This process has been most successful in the tropical Pacific and southern hemisphere. However, it should be noted that there are areas, such as the tropical Atlantic, that have almost no buoy SST observations.
In situ and satellite observations are sparse near the ice edge. To supplement these data, sea ice information is used on a 2° grid. If a grid box is ice covered (concentration of 50% or greater), an SST value is generated with a value of -1.8°C, which is the freezing point of seawater with a salinity of 33–34 psu. This range of salinity is typical near the ice edge in the open ocean.
The superior coverage and greater density of satellite SST data would tend to overwhelm the in situ data in most conventional analyses. This would only be a problem if the satellite data have biases on large timescales and space scales. These biases have occurred in the operational satellite data set. The most severe cases occurred following the March–April 1982 eruptions of El Chichon [Reynolds et al., 1989b] and the June 1991 eruptions of Mount Pinatubo [Reynolds, 1993]. The stratospheric aerosols from these eruptions resulted in strong negative biases in the satellite algorithms.
To illustrate the effect of one of these events, the average weekly anomaly from in situ, daytime, and nighttime satellite observations was computed between 20°S and 20°N during the period with strong stratospheric aerosols from Mount Pinatubo [see Reynolds, 1993]. The results (Figure C2) show that the SST anomalies were all tightly grouped during May and June 1991. After this period the in situ anomaly remained relatively constant while the day and night satellite anomalies became more negative. The nighttime anomalies reached a minimum during September; the daytime retrievals reached a minimum during August. The difference between the in situ and satellite anomalies shows that the satellite observations had average negative biases with magnitudes > 1°C in the tropics in August and September 1991. An attempt was made on October 3, 1991, to correct the nighttime algorithm. However, as shown in Figure C2, this correction was only partially effective. As discussed by Reynolds [1993], this correction led to other satellite biases in the southern hemisphere midlatitudes. The aerosols and the associated tropical biases gradually became weaker until the biases became negligible in April 1992.
Figure C2: SST anomalies obtained from weekly in situ, daytime, and nighttime satellite observations. The anomalies are averaged between 20°S and 20°N from May 1981 to May 1992 [from Reynolds, 1993].
The NCEP analysis of Reynolds [1988] and Reynolds and Marsico [1993] used Poisson's equation to remove any satellite biases relative to the in situ data before combining the two types of data. This analysis, henceforth called the blend, was produced monthly from January 1982 to December 1994 on a 2° grid with an effective spatial resolution of 6°. In this procedure the analysis resolution was degraded to a resolution that could be supported by the in situ data.
To improve this resolution, an optimum interpolation (OI) analysis was developed [Reynolds and Smith, 1994]. The OI is done weekly on a 1° grid and uses the same data that were used by the blend. To correct for satellite biases, a preliminary step using the blended method provides a smooth correction with 12° resolution for each week. The satellite data are adjusted by this correction and used in the OI along with the in situ data. In the next step, OI error statistics are assigned to each type of data (ship, buoy, etc.). The random in situ and satellite data errors are comparable. Hence, because the satellite distribution is so much better than the in situ distribution, the satellite data overwhelm the in situ data in the OI. The OI also weights the nighttime temperatures more since the diurnal cycle is not fully resolved and the daytime temperatures tend to be noisier.
The OI has now been computed from November 1981 to the present. As an example, the analysis corresponding to the data coverages shown in Figure C1 was presented earlier in Figure 4. November 1981 was selected as the starting point of the OI analysis because that is the date the AVHRR data first became operational. For comparison the OI has also been computed without the preliminary satellite bias correction. This analysis will be referred to as OI-UC, where UC stands for uncorrected.
To verify the accuracy of the differences among the blend and the two versions of the OI, monthly SST anomalies from the analyses are compared with independent data. These data are the monthly averaged SST anomalies from TOGA-TAO equatorial current moorings [McPhaden, 1993a]. Three locations have been selected with the longest records: 110°W, 140°W, and 165°E. The monthly root-mean-square (rms) difference between buoys and each of the three analyses (blend, OI, and OI-UC) are computed for the period January 1982 to January 1993 and for each month. The results are summarized in Table C1 for a high aerosol year, 1991, and for the entire period. In all cases the OI is superior to both the OI-UC and the blend. The OI is superior to the blend because of its better resolution. The spatial gradients are greater in the eastern than in the western Pacific, so analysis differences between the blend and the OI are greater at 110°W and 140°W than at 165°E. In years without strong satellite biases the OI and OI-UC analyses behave similarly. However, the large biases during periods such as 1991 cause the degradation of OI-UC analysis relative to both the OI and the blend.
Table C1. Monthly rms Differences Between SSTs From Current Meter Moorings and From NCEP Analyses
The OI analysis with the satellite bias correction yields high-quality global SST fields. These SST fields are widely used for climate monitoring, prediction, and research as well as specifying the surface boundary condition for numerical weather prediction. They appear in many publications, e.g., the NCEP Climate Prediction Center's Climate Diagnostic Bulletin, and are freely available to any user. The SST fields have also been used in atmospheric reanalyses at NCEP, ECMWF, and the U.S. Navy.
In addition, the OI fields have also been used to improve SST analyses from 1950 to 1981 when satellite data were not available. In this method, spatial patterns from empirical orthogonal functions (EOFs) are obtained from the OI fields. The dominant EOF modes (which correspond to the largest variance) are used as basis functions and are fit in a least squares sense to the in situ data to determine the time dependence of each mode. A complete field of SST is then reconstructed from these spatial and temporal modes as described by Smith et al. [1996].
At the beginning of the TOGA project in 1985 it seemed unlikely that satellite altimetry would play much of a role in the ocean observing system. No altimeters had flown since Seasat 7 years earlier. The proposed Seasat-like Navy Remote Ocean Sensing System (NROSS) collapsed under the weight of its enormous budget. NASA had struggled for years, without success, to obtain approval for its dedicated ocean topography altimeter TOPEX, and the French were having similar problems with their counterpart, known as POSEIDON. The U.S. Navy was preparing for the launch of Geosat in March 1985, but this was to be a classified geodetic mission, and it was doubtful that any of the data would be available to the scientific community. On a positive note the European Space Agency (ESA) had just begun building ERS-1 with its altimeter, but the mission was several years behind its original 1987 launch schedule. Given this background, it is easy to understand why TOGA planned to rely so heavily on in situ observations rather than remote sensing.
Despite these inauspicious beginnings, satellite altimetry ultimately provided global observations during 8 of the 10 TOGA years, the gap occurring during 1989–1991 between Geosat and ERS-1. Some of the Geosat data were initially classified, but today they are available in their entirety, spanning the first 4 years of the TOGA project. The Geosat era turned out to be one of the more interesting times in the tropical Pacific cycle because it included a normal period (1985 through mid-1986) followed by distinct ENSO warm and cold events in 1986–1987 and 1988–1989, respectively. ERS-1 became operational in 1991 just as another warm event was beginning, and the TOPEX/POSEIDON observations began in 1992. With the successful launch of ERS-2 in 1995, three altimeters were collecting data simultaneously by middecade, with excellent prospects for a continuous series of altimeters to be in place for the foreseeable future. As shown in Figure C3, it has been possible to connect the various altimeter missions to generate a consistent, long-term record of sea level variations throughout the tropics.
Figure C3: Sea level time series computed from Geosat, ERS-1, and TOPEX/POSEIDON altimeter data (solid line) near the Honiara tide gauge (dashed line) in the western tropical Pacific (taken from Lillibridge et al. [1994]).
The spatial and temporal sampling patterns have varied among these missions as summarized by Koblinsky et al. [1992], but of more fundamental importance is their relative accuracies. It is useful to begin with TOPEX/POSEIDON, as this highly accurate altimeter system has set the standard by which all others are being measured. Primarily because of advances in orbit determination, TOPEX/POSEIDON is able to measure sea level with an absolute accuracy of 4 cm for 1-s averages [Fu et al., 1994; Tapley et al., 1996]. For monthly means in 2° squares the figure is closer to 2 cm [Cheney et al., 1994], and global sea level is being monitored at the level of a few millimeters [Nerem et al., 1997]. Geosat and ERS-1, even after recent orbit improvements [Scharoo et al., 1994; Williamson and Nerem, 1994] are only accurate to 10–15 cm in an absolute sense for the 1-s data. But simple adjustments [Lillibridge et al., 1994] and other sophisticated processing techniques [Tai and Kuhn, 1995] have increased the net accuracy to 5 cm or less for determination of monthly mean sea level variations. Furthermore, much of the ERS-1 error can be removed by adjusting the profiles relative to concurrent TOPEX/POSEIDON data [Le Traon et al., 1995]. For most tropical ocean applications the result is a nearly continuous altimetric record of sea level variability, which can be assimilated in ocean models to improve initial conditions for climate forecasting [Fu and Cheney, 1995].
Special altimeter validation efforts were undertaken during TOGA in recognition of the fact that accuracy requirements might be higher for sea level near the equator than elsewhere in the world ocean. The primary goal of satellite altimetry missions is the study of large-scale ocean circulation, through estimation of the surface geostrophic currents. Geostrophic estimates of surface flow will be very sensitive to small sea level errors near the equator, however, because of the vanishing of the horizontal component of the Coriolis force [e.g., Picaut et al., 1989]. A rigorous open-ocean validation experiment was therefore conducted in the western equatorial Pacific Ocean during the verification phase of the TOPEX/POSEIDON mission to examine the accuracy of the altimetry measurements in the TOGA domain. Two TAO moorings were outfitted with additional temperature, salinity, and pressure sensors to measure within 1 cm the dynamic height from the surface to the bottom at 5-min intervals directly beneath two TOPEX/POSEIDON crossovers; bottom pressure sensors and inverted echo sounders were deployed as well [Katz et al., 1995a; Picaut et al., 1995]. Instantaneous comparisons with the 1-s TOPEX/POSEIDON altimeter retrievals and the 5-min dynamic height resulted in a root-mean-square difference as low as 3.3 cm at 2°S–164°E and 3.7 cm at 2°S–156°E. After the use of a 30-day low-pass filter, in situ and satellite data were found to be highly correlated, with rms differences of < 2 cm.
The applicability of satellite altimeter data for estimating zonal surface current variability at the equator was also assessed using the meridionally differenced form of the geostrophic momentum balance [Picaut et al., 1990; Delcroix et al., 1991, 1992; Menkes et al., 1995]. These studies indicated that altimetry-derived geostrophic zonal current estimates agreed well with near-surface zonal currents observed from TAO moorings along the equator. Given the sensitivity of the geostrophic approximation to small sea level variations near the equator, these results represent the most stringent test of using altimetry observations to estimate sea level and surface currents anywhere in the world ocean.
For several years before the beginning of TOGA, there was optimism that the 1978 success of Seasat, which, for the first time, recorded surface wind velocity over the global ocean [Chelton et al., 1989], would be followed by another satellite wind velocity measuring system. In 1986, cancellation of the NROSS mission, which was to have carried a NSCAT to measure surface wind velocity, created a requirement to implement an in situ surface wind velocity measurement system throughout the equatorial Pacific. This requirement was in part met by development of the TOGA-TAO array [Hayes et al., 1991a; McPhaden, 1993a] using moored wind measurement technology developed in earlier Pacific climate studies [Halpern, 1988b].
The inability during TOGA to launch NSCAT, which was intended to provide global coverage of 25-km-resolution surface wind velocity every 3 days, was partially mitigated with the July 1991 launch of ERS-1. Monthly mean ERS-1 wind speed and direction are accurate to about 1 m s-1 and 35°. However, at wind speeds below 2–3 m s-1, accuracy is poor because the intensity of Bragg scattering has little variation with wind speed. However, ERS-1 data yielded the first opportunity to learn about the detailed space-time structures of intraseasonal surface westerly wind bursts along the Pacific equator [Liu et al., 1996].
In the interim from the beginning of TOGA to the launch of ERS-1, special sensor microwave imager (SSM/I) surface wind speed measurements, which have been recorded since July 1987, have been combined with wind directions [Atlas et al., 1991]. The Atlas et al. [1991] SSM/I surface wind velocity data product, which Busalacchi et al. [1993] demonstrated to be an alternate source of wind vector information, yielded sea surface temperatures, simulated from an ocean general circulation model, that were more representative than those created with a numerical weather prediction surface wind data product [Liu et al., 1996].
The ERS-1 scatterometer and the SSM/I represent active and passive microwave wind-measuring tech- niques, respectively. Another active microwave method is produced with the radar altimeter, which is of secondary importance for studies of large-scale ocean circulation because of the very small coverage in the cross-track direction. SSM/I and ERS-1 wind data are determined over distances > 500 km perpendicular to the ground track, with an areal coverage nearly 100 times greater than that of an altimeter.
One of the objectives of TOGA was to resolve the three-dimensional structure of planetary-scale disturbances along the equator so that daily wind profiles taken at a sufficiently dense horizontal scale were required. The distribution of existing WWW sites was of particular concern in the equatorial Pacific, having gaps which needed attention. Owing to the lack of suitable island sites and considering the logistic difficulty and expense of some of the candidate islands, only some of these gaps could be filled.
During the first few years of TOGA the International TOGA Project Office, with the assistance of many countries, concentrated on setting up observing capability at a number of sites: Kanton Island (Republic of Kiribati) and San Cristobal in the Galapagos, Gan in the Maldive Islands, and Penrhyn Islands. In addition, wind profilers were planned for a number of Pacific Islands (see section D2). These plans were set out in the first edition of the "TOGA International Implementation Plan" and were revised in later editions as circumstances changed. The final list of upper-air sites labeled as Key Stations for TOGA is given in the fourth and final edition of the "Implementation Plan" [International TOGA Project Office, 1992].
Two data sets were produced as a result of the data management of TOGA observations. Upper air reports transmitted on the GTS of the WWW were incorporated in the synoptic-time analyses and forecasts made by the operational forecast centers. The official TOGA archive of these data and the resulting analyses are those produced by the ECMWF. Another data set now exists at NCDC in Asheville, North Carolina, as a result of the Comprehensive Aerological Reference Data Set (CARDS) Program. This data set consists of all soundings made by the WWW and supplemental sites as forwarded by GTS and delayed mode to NCDC. Unfortunately, the CARDS rawinsonde data are spotty and concentrated in the last years of the TOGA experiment. The CARDS archive is available for use in research programs and, in particular, for current and future reanalysis efforts.
In 1985 the NOAA Aeronomy Laboratory in Boulder, Colorado, began to apply newly developed wind profiler technology to the TOGA program to support studies of the tropical atmosphere and climate system [Gage et al., 1990, 1991a]. The first step was taken at Christmas Island in the central Pacific Ocean island republic of Kiribati. A 50-MHz VHF wind profiler was constructed on Christmas Island in 1985 and has been operated nearly continuously since April 1986 [Gage et al., 1994a]. The VHF wind profiler observes horizontal and vertical velocities in the altitude range 1.8–18 km.
Christmas Island is located just north of the equator in the Line Islands south of Hawaii, as shown in Figure 5. The weather on Christmas Island is influenced by its location in the equatorial dry zone associated with the cold tongue of equatorial waters extending from the eastern Pacific across the central Pacific. Substantial rain occurs at Christmas Island only during ENSO warm events when the trade wind circulation relaxes and the cold tongue disappears. Some rain occurs in most years during March–May, when the Intertropical Convergence Zone (ITCZ) makes its closest approach to the equator. The wind profiler was placed at Christmas Island to determine the climatology of tropical wind fields and to observe the natural variability of winds over the central Pacific on the ENSO timescale.
Wind-profiling radars observe weak backscatter from turbulent irregularities in the atmospheric radio refractive index [see, e.g., Gage et al., 1990]. Wind velocity is inferred from the Doppler shift of the backscattered power in the direction of the radar beam. Most wind profilers operate with several fixed beams. Vertically directed beams are utilized for the measurement of vertical motions. Oblique beams (typically directed 15° off-zenith in orthogonal vertical planes) are utilized for the measurement of horizontal motions, since vertical motions are typically very small. In routine operation, orthogonal wind components are sampled every few minutes and processed to yield a consensus mean hourly wind. Typical precision expected for individual wind profiler measurements of horizontal velocities is close to 1 m s-1 [Strauch et al., 1987]. Four times per day, hourly averaged Christmas Island wind data are telemetered via geostationary satellite and incorporated onto the GTS for worldwide distribution.
The Christmas Island wind profiler has served as a prototype for a complementary array of VHF wind profilers that was designed to span the Pacific basin from Indonesia to Peru. This Trans-Pacific Profiler Network was constructed with support from the National Science Foundation. It is comprised of VHF wind profilers at Pohnpei, Federated States of Micronesia; Biak, Indonesia; and Piura, Peru.
Island-based profilers are subject to local influences that may affect their ability to measure representative samples of the large-scale wind field. The magnitude of the local effects generally can be expected to decrease with height and depend on the location of the profiler and the size and topography of the island. For example, Balsley and Carter [1989] found lee waves in the vertical velocities that were pronounced at Pohnpei, an island with substantial topography, but absent at Christmas Island, which is very flat. Additional research is needed to quantify island influences on island-based profiler observations.
In order to observe the winds in the tropical lower troposphere the Aeronomy Laboratory developed an UHF boundary layer wind profiler to complement the VHF wind profiler [Ecklund et al., 1988, 1990]. The new UHF profiler operates at 915 MHz and observes winds in the lower troposphere up to 5–6 km with good vertical resolution. The 915-MHz profiler was installed at Christmas Island in 1990. Together the two profilers observe the entire tropical troposphere. UHF wind profilers are much more sensitive to hydrometeors than are VHF wind profilers; it is necessary to account for the fall speed of hydrometeors with UHF profilers to obtain accurate wind velocities when hydrometeors dominate the radar returns. Since the UHF profilers are very sensitive to hydrometeors [Gage et al., 1994b, 1996a; Ecklund et al., 1995], they are increasingly being used for precipitation studies in the tropics [Williams et al., 1995].
Technical aspects of the development of the 915-MHz UHF profiler are reviewed by Carter et al. [1995]. The profiler was adapted to shipboard operation [Carter et al., 1992] and integrated with a balloon sounding system and a suite of surface instruments to create an integrated sounding system (ISS), which formed a major part of the upper air sounding system used for TOGA COARE [Webster and Lukas, 1992; Parsons, 1994]. ISSs were operated for COARE on Kavieng and Manus Islands in Papua New Guinea, on Kapingamarangi in the Federated States of Micronesia, and on the Island Republic of Nauru in the central Pacific. Intercomparisons of UHF profiler wind and temperature measurements with balloon soundings at ISS sites show very good agreement during COARE [Riddle et al., 1996].
Acknowledgments. The authors would like to thank three anonymous reviewers for their helpful comments on an earlier version of this manuscript. Also, Todd Mitchell of the Joint Institute for the Study of the Atmosphere and Ocean, University of Washington, provided many valuable suggestions on improving the readability of the paper. Scientific oversight for development of the TOGA Observing System was provided by the International TOGA Scientific Steering Group, and implementation was coordinated by International TOGA Project Office (ITPO). We would like to acknowledge John Marsh, director of the ITPO, for his dedicated and enthusiastic service in support of the TOGA program and in particular for his unflagging efforts on behalf of the many individuals and institutions involved in implementing the TOGA Observing System. Financial and other national contributions to TOGA were coordinated through the International TOGA Board. Sponsors for the TOGA Observing System included, in the United States, the National Oceanic and Atmospheric Administration (Office of Global Programs and Office of Oceanic and Atmospheric Research), the National Aeronautics and Space Administration, and the National Science Foundation; in France, L'Institut Français de Recherche pour le Développement en Coopération (ORSTOM), the Programme National de Dynamique du Climat, the Ministère de la Recherche et de l'Enseignement Supérieur, and the Institut Français de Recherche pour l'Exploitation des Océans; in Japan, the Science and Technology Agency and the Japan Marine Science and Technology Center; in Korea, the Ministry of Science and Technology; in Taiwan, the National Science Council; in Australia, the Commonwealth Scientific and Industrial Research Organization, the Royal Australian Navy, and the Bureau of Meteorology; and organizations too numerous to list in many other countries that participated in the 10-year TOGA program. This is PMEL contribution 1720.
Aceituno, P., El Niño, Southern Oscillation and ENSO: Confusing names for a complex ocean-atmosphere interaction, Bull. Am. Meteorol. Soc., 73, 483–485, 1992.
Alexander, M. A., Mid-latitude ocean-atmosphere interaction during El Niño, 1, The North Pacific Ocean, J. Clim., 5, 944–958, 1992.
Allen, M. R., S. P. Lawrence, M. J. Murray, C. T. Mutlow, T. N. Stockdale, D. T. Llewellyn-Jones, and D. L. T. Anderson, Control of tropical instability waves in the Pacific, Geophys. Res. Lett., 22, 2581–2584, 1995.
Anderson, D., TAO data assimilation at ECMWF, in Proceedings of the Second Workshop of the TOGA-TAO Implementation Panel, M. J. McPhaden (Ed.), Bali, Indonesia, October 18–20, 1993, ITPO Publication No. 10, Pac. Mar. Environ. Lab., Seattle, Wash., p. 20–21, 1994.
Anderson, S. P., R. A. Weller, and R. B. Lukas, Surface buoyancy forcing and the mixed layer of the western Pacific warm pool: Observations and 1D model results, J. Clim., 9, 3056–3085, 1996.
Ando, K., and M. J. McPhaden, Variability of the surface layer hydrography in the tropical Pacific Ocean, J. Geophys. Res., 102, 23,063–23,078, 1997.
Angevine, W. M., S. K. Avery, W. L. Ecklund, and D. A. Carter, Fluxes of heat and momentum measured with a boundary layer wind profiler radar/RASS, J. Appl. Meteorol., 32, 73–80, 1993.
Angevine, W. M., A. B. White, and S. K. Avery, Boundary layer depth and entrainment zone characterization with a boundary layer profiler, Boundary Layer Meteorol., 68, 375–385, 1994.
Arnault, S., and C. Perigaud, Altimetry and models in the tropical oceans: A review, Oceanol. Acta, 15, 411–430, 1992.
Atlas, R., S. C. Bloom, R. N. Hoffman, J. V. Ardizzone, and G. Brin, Space-based surface wind vectors to aid understanding of air-sea interactions, Eos Trans. AGU, 72, 201–208, 1991.
Atlas, R., R. N. Hoffman, S. C. Bloom, J. C. Jusem, and J. Ardizzone, A multi-year global surface wind velocity data set using SSM/I wind observations, Bull. Am. Meteorol. Soc., 77, 869–882, 1996.
Bailey, R., A. Gronell, H. Phillips, E. Tanner, and G. Meyers, Quality control cookbook for XBT data, Rep. 221, Mar. Lab., Div. of Oceanogr., Commonw. Sci. and Ind. Res. Organ., Hobart, Tasmania, Australia, 1994.
Baker, D. J., Ocean instruments and experiment design, in Evolution of Physical Oceanography, edited by B. A. Warren and C. Wunsch, pp. 396–433, MIT Press, Cambridge, Mass., 1981.
Balmaseda, M. A., M. K. Davey, and D. L. T. Anderson, Decadal and seasonal dependence of ENSO prediction skill, J. Clim., 8, 2705–2715, 1995.
Balsley, B. B., and D. A. Carter, Mountain waves in the tropical Pacific atmosphere: A comparison of vertical wind fluctuations over Pohnpei and Christmas Island using VHF wind profilers, J. Atmos. Sci., 46, 2698–2715, 1989.
Balsley, B. B., W. L. Ecklund, D. A. Carter, A. C. Riddle, and K. S. Gage, Average vertical motions in the tropical atmosphere observed by a radar wind profiler on Pohnpei (7°N latitude, 157°E longitude), J. Atmos. Sci., 45, 396–405, 1988.
Barber, R. T., and F. P. Chavez, Biological consequences of El Niño, Science, 222, 1203–1210, 1983.
Barnett, T. P., Interaction of the monsoon and Pacific trade wind system on interannual time scales, I, The equatorial zone, Mon. Weather Rev., 111, 756–773, 1983.
Bates, J., High-frequency variability of special sensor microwave/imager derived wind speed and moisture during an intraseasonal oscillation, J. Geophys. Res., 96, 3411–3423, 1991.
Battisti, D. S., Dynamics and thermodynamics of a warming event in a coupled atmosphere-ocean model, J. Atmos. Sci., 45, 2889–2919, 1988.
Battisti, D. S., and A. C. Hirst, Interannual variability in a tropical atmosphere-ocean model: Influence of the basic state, ocean geometry and nonlinearity, J. Atmos. Sci., 46, 1687–1712, 1989.
Bentamy, A., Y. Quilfen, F. Gohin, N. Grima, M. Lenaour, and J. Servain, Determination and validation of average wind fields from ERS-1 scatterometer measurements, J. Global Atmos. Ocean Syst., 4, 1–29, 1996.
Berrit, G., Contribution à la connaissance des variations saisonnières dans le golf de Guinée, Observations de surface le long des lignes de navigation, 1, generalités, Cah. Oceanogr., 13, 715–727, 1961.
Bjerknes, J., A possible response of the atmospheric Hadley circulation to equatorial anomalies of ocean temperature, Tellus, 18, 820–829, 1966.
Bjerknes, J., Atmospheric teleconnections from the equatorial Pacific, Mon. Weather Rev., 97, 163–172, 1969.
Blanke, B., and P. Delecluse, Variability of the tropical Atlantic Ocean simulated by a general circulation model with two different mixed layer physics, J. Phys. Oceanogr., 23, 1363–1388, 1993.
Bond, N. A., and M. J. McPhaden, An indirect estimate of the diurnal cycle in upper ocean turbulent heat fluxes at the equator, 140°W, J. Geophys. Res., 100, 18,369–18,378, 1995.
Boulanger, J.-P., and L.-L. Fu, Evidence of boundary reflection of Kelvin and first-mode Rossby waves from TOPEX/POSEIDON sea level data, J. Geophys. Res., 101, 16,361–16,371, 1996.
Boulanger, J.-P., and C. Menkes, Propagation and reflection of long equatorial waves in the Pacific Ocean during the 1992–1993 El Niño, J. Geophys. Res., 100, 25,041–24,059, 1995.
Boutin, J., and J. Etcheto, Consistency of Geosat, SSM/I and ERS1 global surface wind speeds: Comparison with in-situ data, J. Atmos. Oceanic Technol., 13, 183–187, 1996.
Braconnot, P., and C. Frankignoul, On the ability of the LODYC GCM to simulate the thermocline depth in the equatorial Atlantic, Clim. Dyn., 9, 221–234, 1994.
Brady, E. C., and P. R. Gent, The seasonal cycle of meridional heat transport in a numerical model of the Pacific equatorial upwelling zone, J. Phys. Oceanogr., 24, 2658–2673, 1994.
Bryden, H. L., and E. C. Brady, Diagnostic model of the three-dimensional circulation in the upper equatorial Pacific Ocean, J. Phys. Oceanogr., 15, 1255–1273, 1985.
Bryden, H. L., and E. L. Brady, Eddy momentum and heat fluxes and their effects on the circulation of the equatorial Pacific Ocean, J. Mar. Res., 47, 55–79, 1989.
Busalacchi, A. J., Data assimilation in support of tropical ocean circulation studies, in Modern Approaches to Data Assimilation in Ocean Modeling, pp. 235–270, Elsevier Sci., New York, 1996.
Busalacchi, A. J., and M. A. Cane, Hindcasts of sea level variations during the 1982–83 El Niño, J. Phys. Oceanogr., 15, 213–221, 1985.
Busalacchi, A. J., and J. J. O'Brien, Seasonal variability in a model of the tropical Pacific, J. Phys. Oceanogr., 10, 1929–1952, 1980.
Busalacchi, A. J., and J. J. O'Brien, Interannual variability of the equatorial Pacific in the 1960s, J. Geophys. Res., 86, 10,901–10,907, 1981.
Busalacchi, A. J., K. Takeuchi, and J. J. O'Brien, Interannual variability of the equatorial Pacific-Revisited, J. Geophys. Res., 88, 7551–7562, 1983.
Busalacchi, A. J., M. J. McPhaden, J. Picaut, and S. Springer, Sensitivity of wind-driven tropical Pacific Ocean on seasonal and interannual time-scales, J. Mar. Syst., 1, 119–154, 1990.
Busalacchi, A. J., R. M. Atlas, and E. C. Hackert, Comparison of SSM/I vector wind stress with model-derived and subjective products for the tropical Pacific, J. Geophys. Res., 98, 6961–6977, 1993.
Busalacchi, A. J., M. J. McPhaden, and J. Picaut, Variability in equatorial Pacific sea surface topography during the verification phase of the TOPEX/POSEIDON mission, J. Geophys. Res., 99, 24,725–24,738, 1994.
Cane, M. A., Oceanographic events during El Niño, Science, 222, 1189–1195, 1984.
Cane, M. A., and S. E. Zebiak, A theory for El Niño and the Southern Oscillation, Science, 228, 1085–1087, 1985.
Cane, M. A., S. C. Dolan, and S. E. Zebiak, Experimental forecasts of the 1982/83 El Niño, Nature, 321, 827–832, 1986.
Cane, M. A., A. Clement, A. Kaplan, Y. Kushnir, D. Pozdnyakov, R. Seager, S. Zebiak, and R. Murtugudde, 20th century sea surface temperature trends, Science, 275, 957–960, 1997.
Cardone, V. J., J. G. Greenwood, and M. A. Cane, On trends in historical marine wind data, J. Clim., 3, 113–127, 1990.
Carter, D. A., W. L. Ecklund, K. S. Gage, M. Spowart, H. L. Cole, E. F. Chamberlain, W. F. Dabberdt, and J. Wilson, First test of a shipboard wind profiler, Bull. Am. Meteorol. Soc., 73, 1587–1592, 1992.
Carter, D. A., K. S. Gage, W. L. Ecklund, W. M. Angevine, P. E. Johnston, A. C. Riddle, J. Wilson, and C. R. Williams, Developments in lower tropospheric wind profiling at NOAA's Aeronomy Laboratory, Radio Sci., 30, 977–1001, 1995.
Carter, W., W. Scherer, and J. Diamante, Measuring absolute sea level, Sea Technol., 28, 52–54, 1987.
Carton, J. A., and B. Huang, Warm events in the tropical Atlantic, J. Phys. Oceanogr., 24, 888–903, 1994.
Carton, J. A., and E. J. Katz, Estimates of the zonal slope and the seasonal transport of the Atlantic North Equatorial Countercurrent, J. Geophys. Res., 95, 3091–3100, 1990.
Carton, J. A., B. S. Giese, X. Cao, and L. Miller, Impact of altimeter, thermistor, and expendable bathythermograph data on retrospective analyses of the tropical Pacific Ocean, J. Geophys. Res., 101, 14,147–14,159, 1996.
Cassou, C., C. Perigaud, L. L. Fu, and J. P. Boulanger, El Niño events over 1980–1995 simulated and forecasted with a simple coupled ocean-atmosphere model, Eos Trans. AGU, 77(46), Fall Meet. Suppl., F385, 1996.
Chabbra, N. K., J. M. Dahlen, J. R. Scholten, Calibration of the Draper Laboratory low cost drifter (LCD), Rep. CSDL-R-1906, 137 pp., Charles Stark Draper Lab., Inc., Cambridge, Mass., 1987.
Chang, P., Seasonal cycle of sea surface temperature and mixed layer heat budget in the tropical Pacific Ocean, Geophys. Res. Lett., 20, 2079–2082, 1993.
Chang, P., A study of the seasonal cycle of sea surface temperature in the tropical Pacific Ocean using reduced gravity models, J. Geophys. Res., 99, 7725–7741, 1994.
Chang, P., L. Ji, B. Wang, and T. Li, Interactions between the seasonal cycle and El Niño-Southern Oscillation in an intermediate coupled ocean atmosphere model, J. Atmos. Sci., 52, 2353–2372, 1995.
Chao, Y., and S. G. H. Philander, On the contrast between the seasonal cycles of the equatorial Atlantic and Pacific Oceans, J. Phys. Oceanogr., 21, 1399–1406, 1991.
Chelton, D., and R. Davis, Monthly mean sea level variability along the west coast of North America, J. Phys. Oceanogr., 12, 757–784, 1982.
Chelton, D., M. Freilich, and J. Johnson, Evaluation of unambiguous vector winds from the Seasat scatterometer, J. Atmos. Oceanic Technol., 6, 1024–1039, 1989.
Chen, D., A. J. Busalacchi, and L. M. Rothstein, The roles of vertical mixing, solar radiation, and wind stress in a model simulation of the sea surface temperature seasonal cycle in the tropical Pacific Ocean, J. Geophys. Res., 99, 20,345–20,359, 1994a.
Chen, D., L. W. Rothstein, and A. J. Busalacchi, A hybrid vertical mixing scheme and its application to tropical ocean models, J. Phys. Oceanogr., 24, 2156–2179, 1994b.
Chen, D., S. E. Zebiak, A. J. Busalacchi, and M. A. Cane, An improved procedure for El Niño forecasting, Science, 269, 1699–1702, 1995.
Cheney, R. E., L. Miller, B. C. Douglas, and R. W. Agreen, Monitoring equatorial Pacific sea level with Geosat, Johns Hopkins APL Tech. Dig., 8, 245–250, 1987.
Cheney, R. E., B. C. Douglas, and L. Miller, Evaluation of Geosat data with application to tropical Pacific sea level variability, J. Geophys. Res., 94, 4737–4747, 1989.
Cheney, R. E., L. Miller, R. W. Agreen, N. S. Doyle, and J. L. Lillibridge, TOPEX/POSEIDON: The 2-cm solution, J. Geophys. Res., 99, 24,555–24,563, 1994.
Chereskin, T., P. P. Niiler, and P. Poulain, A numerical study of the effects of upper ocean shear on flexible drogue drifters, J. Atmos. Oceanic Technol., 6, 243–253, 1989.
Clarke, A., On the reflection and transmission of low-frequency energy at the irregular western Pacific Ocean boundary, J. Geophys. Res., 96, 3289–3305, 1991.
Clarke, A., Low-frequency reflection from a nonmeridional eastern ocean boundary and the use of coastal sea level to monitor eastern Pacific equatorial Kelvin waves, J. Phys. Oceanogr., 22, 163–183, 1992.
Clarke, A., and X. Liu, Observations and dynamics of semiannual and annual sea levels near the eastern equatorial Indian Ocean boundary, J. Phys. Oceanogr., 23, 386–399, 1993.
Clarke, A. J., and X. Liu, Interannual sea level in the northern and eastern Indian Ocean, J. Phys. Oceanogr., 24, 1224–1235, 1994.
Clarke, A. J., and S. Van Gorder, On ENSO coastal currents and sea levels, J. Phys. Oceanogr., 24, 661–680, 1994.
Climate Analysis Center, Near real-time analyses, December 1994, U.S. Clim. Diagnostics Bull., 80 pp., U.S. Dep. of Comm., Washington, D.C., 1994.
Cox, M. D., Generation and propagation of 30-day waves in a numerical model of the Pacific, J. Phys. Oceanogr., 10, 1168–1186, 1980.
Cronin, M., and M. J. McPhaden, The upper ocean heat balance in the western equatorial Pacific warm pool during September–December 1992, J. Geophys. Res., 102, 8533–8553, 1997.
Currier, P. E., S. K. Avery, B. B. Balsley, and K. S. Gage, Use of two wind profilers for precipitation studies, Geophys. Res. Lett., 19, 1017–1020, 1992.
da Silva, A. M., C. C. Young, and S. Levitus, Atlas of surface marine data 1994, vol. 1: Algorithms and procedures, NOAA Atlas NESDIS 6, U.S. Dept. of Commerce, Washington, D.C., 83 pp., 1994.
Delcroix, T., and C. Gautier, Estimate of heat content variations from sea level measurements in the central and western tropical Pacific from 1979 to 1985, J. Phys. Oceanogr., 17, 725–734, 1987.
Delcroix, T., and C. Henin, Mechanisms of subsurface thermal structure and sea surface thermohaline variabilities in the southwest Pacific during 1975–85, J. Mar. Res., 47, 777–812, 1989.
Delcroix, T., and C. Henin, Seasonal and interannual variations of sea surface salinity in the tropical Pacific Ocean, J. Geophys. Res., 96, 22,135–22,150, 1991.
Delcroix, T., and J. Picaut, Zonal displacement of the western equatorial Pacific "fresh pool," J. Geophys. Res., 103, 1087–1098, 1998.
Delcroix, T., J. Picaut, and G. Eldin, Equatorial Kelvin and Rossby waves evidenced in the Pacific Ocean through sea level and surface current anomalies, J. Geophys. Res., 96, suppl., 3249–3262, 1991.
Delcroix, T., G. Eldin, M. H. Radenac, J. Toole, and E. Firing, Variations of the western equatorial Pacific Ocean, 1986–1988, J. Geophys. Res., 97, 5423–5445, 1992.
Delcroix, T., G. Eldin, M. J. McPhaden, and A. Morliere, Effects of westerly wind bursts upon the western equatorial Pacific Ocean, February–April 1991, J. Geophys. Res., 98, 16,379–16,386, 1993.
Delcroix, T., J.-P. Boulanger, F. Masia, and C. Menkes, Geosat-derived sea level and surface current anomalies in the equatorial Pacific during the 1986–1989 El Niño and La Niña, J. Geophys. Res., 99, 25,093–25,107, 1994.
Delcroix, T., C. Henin, V. Porte, and P. Arkin, Precipitation and sea-surface salinity in the tropical Pacific, Deep Sea Res., Part I, 43, 1123–1141, 1996.
Delecluse, P., J. Servain, C. Levy, K. Arpe, and L. Bengsston, On the connection between the 1984 Atlantic warm event and the 1982–83 ENSO, Tellus, Ser. A, 46, 448–464, 1994.
Derber, J. D., and A. Rosati, A global oceanic data assimilation system, J. Phys. Oceanogr., 19, 1333–1347, 1989.
Deser, C., Daily surface wind variations over the equatorial Pacific Ocean, J. Geophys. Res., 99, 23,071–23,078, 1994.
Deser, C., and J. M. Wallace, El Niño events and their relation to the Southern Oscillation: 1925–1986, J. Geophys. Res., 92, 14,189–14,196, 1987.
Deser, C., J. J. Bates, and S. Wahl, The influence of sea surface temperature gradients on stratiform cloudiness along the equatorial front in the Pacific Ocean, J. Clim., 6, 1172–1180, 1993.
Dessier, A., and J. R. Donguy, Response to El Niño signals of the epiplanktonic copepod populations in the eastern tropical Pacific, J. Geophys. Res., 92, 14,393–14,403, 1987.
Dessier, A., and J. R. Donguy, The sea surface salinity in the tropical Atlantic between 10°S and 30°N-seasonal and interannual variations (1977–1989), Deep Sea Res., Part I, 41, 81–100, 1994.
Donguy, J. R., Recent advances in the knowledge of the climatic variations in the tropical Pacific Ocean, Prog. Oceanogr., 19, 49–85, 1987.
Donguy, J. R., Surface and subsurface salinity in the tropical Pacific Ocean: Relations with climate, Prog. Oceanogr., 34, 45–78, 1994.
Donguy, J. R., and G. Meyers, Observations of geostrophic transport variability in the western tropical Indian Ocean, Deep Sea Res., Part I, 42, 1007–1028, 1995.
Donguy, J. R., and G. Meyers, Mean annual variation of transport of major currents in the tropical Pacific Ocean, Deep Sea Res., Part I, 43, 1105–1122, 1996a.
Donguy, J. R., and G. Meyers, Seasonal variations of sea-surface salinity and temperature in the tropical Indian Ocean, Deep Sea Res., Part I, 43, 117–138, 1996b.
Donguy, J. R., A. Dessier, and Y. du Penhoat, Heat content displacement in the Pacific during the 1982–83 El Niño event, Oceanol. Acta, 12, 149–157, 1989.
du Penhoat, Y., and M. A. Cane, Effect of low-latitude western boundary gaps on the reflection of equatorial motions, J. Geophys. Res., 96, suppl., 3307–3322, 1991.
du Penhoat, Y., T. Delcroix, and J. Picaut, Interpretation of Kelvin/Rossby waves in the equatorial Pacific from model-Geosat data intercomparison during the 1986–1987 El Niño, Oceanol. Acta, 15, 545–554, 1992.
Ecklund, W. L., D. A. Carter, and B. B. Balsley, A UHF wind profiler for the boundary layer: Brief description and initial results, J. Atmos. Oceanic Technol., 5, 432–441, 1988.
Ecklund, W. L., D. A. Carter, B. B. Balsley, P. E. Currier, J. L. Green, B. L. Weber, and K. S. Gage, Field tests of a lower tropospheric wind profiler, Radio Sci., 25, 899–906, 1990.
Ecklund, W. L., K. S. Gage, and C. R. Williams, Tropical precipitation studies using 915-MHz wind profiler, Radio Sci., 30, 1055–1064, 1995.
Enfield, D. B., Zonal and seasonal variations in the near-surface heat balance of the equatorial ocean, J. Phys. Oceanogr., 16, 1038–1054, 1986.
Enfield, D. B., The intraseasonal oscillation in eastern Pacific sea levels: How is it forced?, J. Phys. Oceanogr., 17, 1860–1876, 1987.
Enfield, D. B., El Niño, past and present, Rev. Geophys., 27, 159–187, 1989.
Enfield, D., and J. Allen, On the structure and dynamics of monthly mean sea level anomalies along the Pacific coast of North and South America, J. Phys. Oceanogr., 10, 557–578, 1980.
Enfield, D. B., and D. A. Mayer, Tropical Atlantic sea surface temperature variability and its relation to El Niño-Southern Oscillation, J. Geophys. Res., 102, 929–945, 1997.
Eriksen, C. C., The Tropic Heat Program: An overview, Eos Trans. AGU, 66, 50, 1985.
Eriksen, C., A review of PEQUOD, in Further Progress in Equatorial Oceanography, edited by E. J. Katz and J. M. Witte, pp. 29–46, Nova Univ. Press, Fort Lauderdale, Fla., 1987.
Eriksen, C. C., M. B. Blumenthal, S. P. Hayes, and P. Ripa, Wind-generated equatorial Kelvin waves observed across the Pacific Ocean, J. Phys. Oceanogr., 13, 1622–1640, 1983.
Esbensen, S. K., and Y. Kushnir, The heat budget of the global ocean: An atlas based on estimates from surface marine observations, Rep. 29, Clim. Res. Inst., Oreg. State Univ., Corvallis, 1981.
Esbensen, S. K., and M. J. McPhaden, Enhancement of tropical ocean evaporation and sensible heat flux by atmospheric mesoscale systems, J. Clim., 9, 2307–2325, 1996.
Feely, R. A., R. Wanninkhof, C. E. Cosca, M. J. McPhaden, R. H. Byrne, F. J. Millero, F. P. Chavez, T. Clayton, D. M. Campbell, and P. P. Murphy, The effect of tropical instability waves on CO2 species distributions along the equator in the eastern equatorial Pacific during the 1992 ENSO event, Geophys. Res. Lett., 21, 277–280, 1994.
Festa, J. F., and R. L. Molinari, An evaluation of the WOCE volunteer observing ship XBT network in the Atlantic, J. Atmos. Oceanic Technol., 9, 305–317, 1992.
Fine, R. A., W. H. Peterson, and H. G. Ostlund, The penetration of tritium into the tropical Pacific, J. Phys. Oceanogr., 17, 553–564, 1987.
Firing, E., R. Lukas, J. Sadler, and K. Wyrtki, Equatorial undercurrent disappears during 1982–83 El Niño, Science, 222, 1121–1122, 1983.
Fischer, M., M. Latif, M. Flügel, and M. Ji, The impact of data assimilation on ENSO simulations and predictions, Mon. Weather Rev., 125, 819–829, 1997.
Flament, P., S. Kennan, R. Knox, P. Niiler, and R. Bernstein, Observations of the three-dimensional structure of tropical instability, Nature, 383, 610–613, 1996.
Flatau, M., P. J. Flatau, P. Phoebus, and P. P. Niiler, The feedback between equatorial convection and local radiative and evaporative processes: The implications for intraseasonal oscillations, J. Atmos. Sci., 54, 2373–2386, 1997.
Foley, D. G., T. D. Dickey, M. J. McPhaden, R. R. Bidigare, M. R. Lewis, R. T. Batber, S. T. Lindley, C. Garside, and D. V. Manov, Time series of physical, bio-optical, and geochemical properties in the central equatorial Pacific Ocean at 0°, 140°W, February 1992–March 1993, Deep Sea Res., in press, 1998.
Frankignoul, C., F. Bonjean, and G. Reverdin, Interannual variability of surface currents in the tropical Pacific during 1987–1993, J. Geophys. Res., 101, 3629–3647, 1996.
Freilich, M., and R. Dunbar, A preliminary C-band scatterometer model function for the ERS-1 AMI instrument, in Proceedings of the First ERS-1 Symposium, Eur. Space Agency Spec. Publ., ESA SP-359, 79–84, 1993.
Freitag, H. P., Y. Feng, L. J. Mangum, M. P. McPhaden, J. Neander, and L. D. Stratton, Calibration procedures and instrumental accuracy estimates of TAO temperature, relative humidity and radiation measurements, Tech. Memo. ERL PMEL-104, 32 pp., Natl. Oceanic and Atmos. Admin., Silver Spring, Md., 1995.
Fu, L.-L., and R. E. Cheney, Application of satellite altimetry to ocean circulation studies: 1987–1994, U.S. Natl. Rep. Int. Union Geod. Geophys. 1991–1994, Rev. Geophys., 33, 213–223, 1995.
Fu, L.-L., I. Fukumori, and R. N. Miller, Fitting dynamic models to the Geosat sea level observations in the tropical Pacific Ocean, II, A linear, wind-driven model, J. Phys. Oceanogr., 23, 2162–2181, 1993.
Fu, L.-L., E. J. Christensen, and C. A. Yamarone, TOPEX/POSEIDON mission overview, J. Geophys. Res., 99, 24,369–24,381, 1994.
Fukumori, I., Assimilation of TOPEX sea level measurements with a reduced-gravity, shallow water model of the tropical Pacific Ocean, J. Geophys. Res., 100, 25,027–25,039, 1995.
Gaffard, C., and H. Roquet, Impact of the ERS-1 scatterometer wind data on the ECMWF 3D-Var assimilation system, Tech. Memo. 217, 21 pp., Eur. Cent. for Medium-Range Weather Forecasts, Reading, England, 1995.
Gage, K.S., Radar observation of the free atmosphere: Structure and dynamics, in Radar in Meteorology, edited by D. Atlas, pp. 534–565, American Meteorological Society, Boston, Mass., 1990.
Gage, K. S., and G. C. Reid, Longitudinal variations in tropical tropopause properties in relation to tropical convection and El Niño-Southern Oscillation events, J. Geophys. Res., 92, 14,197–14,203, 1987.
Gage, K. S., B. B. Balsley, W. L. Ecklund, R. F. Woodman, and S. K. Avery, Wind-profiling Doppler radars for tropical atmospheric research, Eos Trans. AGU, 71, 1851–1854, 1990.
Gage, K. S., B. B. Balsley, W. L. Ecklund, D. A. Carter, and J. R. McAfee, Wind profiler related research in the tropical Pacific, J. Geophys. Res., 96, 3209–3220, 1991a.
Gage, K. S., J. R. McAfee, D. A. Carter, A. C. Riddle, G. C. Reid, and B. B. Balsley, Direct measurements of long-term mean vertical motions over the tropical Pacific using wind-profiling Doppler radar, Science, 254, 1771–1773, 1991b.
Gage, K. S., J. R. McAfee, D. A. Carter, W. L. Ecklund, G. C. Reid, A. C. Riddle, P. E. Johnston, and B. B. Balsley, Wind profiler yields observations of ENSO signal, Eos Trans. AGU, 74, 137, 142, 1993.
Gage, K. S., J. R. McAfee, W. L. Ecklund, D. A. Carter, C. Williams, P. E. Johnston, and A. C. Riddle, The Christmas Island wind profiler: A prototype VHF wind-profiling Doppler radar for the tropics, J. Atmos. Oceanic Technol., 11, 22–31, 1994a.
Gage, K. S., C. R. Williams, and W. L. Ecklund, UHF wind profilers: A new tool for diagnosing tropical convective cloud systems, Bull. Am. Meteorol. Soc., 75, 2289–2294, 1994b.
Gage, K. S., C. R. Williams, and W. L. Ecklund, Application of the 915 MHz profiler for diagnosing and classifying tropical precipitating cloud systems, Meteorol. Atmos. Phys., 59, 141–151, 1996a.
Gage, K. S., J. R. McAfee, and C. R. Williams, On the annual variation of tropospheric zonal winds observed above Christmas Island in the central equatorial Pacific, J. Geophys. Res., 101, 15,061–15,070, 1996b.
Geisler, J. E., M. L. Blackmon, G. T. Bates, and S. Munoz, Sensitivity of January climate response to the magnitude and position of equatorial Pacific sea surface temperature anomalies, J. Atmos. Sci., 42, 1037–1149, 1985. Giese, B. S., and D. E. Harrison, Aspects of Kelvin wave response to episodic wind forcing, J. Geophys. Res., 95, 7289–7312, 1990.
Giese, B. S., and D. E. Harrison, Eastern equatorial Pacific response to three composite westerly wind types, J. Geophys. Res., 96, suppl., 3239–3248, 1991.
Giese, B. S., J. A. Carton, and L. J. Holl, Sea level variability in the eastern tropical Pacific as observed by TOPEX and Tropical Ocean-Global Atmosphere Tropical Atmosphere-Ocean Experiment, J. Geophys. Res., 99, 24,739–24,748, 1994.
Gill, A. E., An estimation of sea-level and surface-current anomalies during the 1972 El Niño and consequent thermal effects, J. Phys. Oceanogr., 13, 586–606, 1983.
Gill, A. E., and P. P. Niiler, A theory of the seasonal variability in the ocean, Deep Sea Res. Oceanogr. Abstr., 20, 141–177, 1973.
Gill, A. E., and E. M. Rasmusson, The 1982–83 climate anomaly in the equatorial Pacific, Nature, 305, 229–234, 1983.
Glantz, M. H. (Ed.), Usable Science: Food Security, Early Warning, and El Niño, Proceedings of the Workshop on ENSO/FEWS, Budapest, Hungary, October 25–28, 1993, Nat. Cent. for Atmos. Res., Boulder, Colo., 1994.
Goddard, L., and N. E. Graham, El Niño in the 1990s, J. Geophys. Res., 102, 10,423–10,436, 1997.
Godfrey, J. S., R. A. Houze Jr., R. H. Johnson, R. Lukas, J.-L. Redelsperger, A. Sumi, and R. Weller, Coupled Ocean-Atmosphere Response Experiment (COARE): An interim report, J. Geophys. Res., this issue.
Goldenberg, S. B., and J. J. O'Brien, Time and space variability of tropical Pacific wind stress, Mon. Weather Rev., 109, 1190–1207, 1981.
Gossard, E. E., Measuring drop-size distributions in clouds with clear-air-sensing Doppler radar, J. Atmos. Oceanic Technol., 5, 640–649, 1988.
Gourdeau, L., J. F. Minster, and M. C. Gennero, Sea level anomalies in the tropical Atlantic from Geosat data assimilated in a linear model, 1986–1988, J. Geophys. Res., 102, 5583–5594, 1997.
Graham, N. E., Simulation of recent global temperature trends, Science, 267, 666–671, 1995.
Graham, N. E., and T. P. Barnett, Sea surface temperature, surface wind divergence, and convection over tropical oceans, Science, 238, 657–659, 1987.
Graham, N. E., and W. B. White, The El Niño cycle: A natural oscillator of the Pacific ocean-atmosphere system, Science, 240, 1293–1302, 1988.
Gray, W. M., C. W. Landsea, P. Mielke, and K. Berry, Predicting Atlantic seasonal hurricane activity 6–11 months in advance, Weather Forecasting, 7, 440–455, 1993.
Greiner, E., and C. Perigaud, Assimilation of Geosat altimetric data in a nonlinear reduced-gravity model of the Indian Ocean, I, Adjoint approach and model-data consistency, J. Phys. Oceanogr., 24, 1783–1804, 1994.
Greiner, E., and C. Perigaud, Assimilation of Geosat altimetric data in a nonlinear shallow-water model of the Indian Ocean, II, Validation and interpretation of assimilated results, J. Phys. Oceanogr., 26, 1735–1746, 1996.
Gu, D., and S. G. H. Philander, Secular changes of annual and interannual variability in the tropics during the past century, J. Clim., 8, 864–876, 1995.
Gu, D., and S. G. H. Philander, Interdecadal climate fluctuations that depend on exchanges between the tropics and extratropics, Science, 275, 805–807, 1997.
Gu, D., S. G. H. Philander, and M. J. McPhaden, The seasonal cycle and its modulation in the eastern Pacific, J. Phys. Oceanogr., in press, 1998.
Gutzler, D. S., and L. M. Hartten, Daily variability of lower tropospheric winds over the tropical western Pacific, J. Geophys. Res., 100, 22,999–23,008, 1995.
Gutzler, D. S., G. N. Kiladis, G. A. Meehl, K. M. Weickmann, and M. Wheeler, The global climate of December 1992–February 1993, II, Large-scale variability across the tropical western Pacific during TOGA COARE, J. Clim., 7, 1606–1622, 1994.
Halpern, D., A Pacific equatorial temperature section from 172°E to 110°W during winter-spring 1979, Deep Sea Res., Part A, 27, 931–940, 1980.
Halpern, D., Comparison of upper ocean VACM and VMCM observations in the equatorial Pacific, J. Atmos. Oceanic Technol., 4, 84–93, 1987a.
Halpern, D., Observations of annual and El Niño thermal and flow variations at 0°, 110°W and 0°, 95°W during 1980–1985, J. Geophys. Res., 92, 8197–8212, 1987b.
Halpern, D., Comparison of moored wind measurements from a spar and toroidal buoy in the eastern equatorial Pacific during February–March 1981, J. Geophys. Res., 92, 8303–8306, 1987c.
Halpern, D., On the accuracy of monthly mean wind speeds over the equatorial Pacific, J. Atmos. Oceanic Technol., 5, 362–367, 1988a.
Halpern, D., Moored surface wind observations at four sites along the Pacific equator between 140°W and 95°W, J. Clim., 1, 1251–1260, 1988b.
Halpern, D., Validation of special sensor microwave imager monthly-mean wind speed from July 1987 to December 1989, IEEE Trans. Geosci. Remote Sens., 31, 692–699, 1993.
Halpern, D., Visiting TOGA's past, Bull. Am. Meteorol. Soc., 77, 233–242, 1996.
Halpern, D., and M. Ji, An evaluation of the National Meteorological Center weekly hindcast of upper-ocean temperature along the eastern Pacific equator in January 1992, J. Clim., 6, 1221–1226, 1993.
Halpern, D., H. P. Freitag, and A. Shepherd, Applications of ARGOS and RAMS measurements in equatorial Pacific ocean-atmosphere interaction studies, in Proceedings of Oceans `84, pp. 736–740, Mar. Technol. Soc., Washington, D.C., 1984.
Halpern, D., R. A. Knox, and D. S. Luther, Observations of 20-day period meridional current oscillations in the upper ocean along the Pacific equator, J. Phys. Oceanogr., 18, 1514–1534, 1988.
Halpern, D., Y. Chao, C.-C. Ma, and C. R. Mechoso, Comparison of tropical Pacific temperature and current simulations with two vertical mixing schemes embedded in an ocean general circulation model and reference to observations, J. Geophys. Res., 100, 2515–2522, 1995.
Halpert, M. S., and C. F. Ropelewski, Surface temperature patterns associated with the Southern Oscillation, J. Clim., 5, 577–593, 1992.
Han, Y.-J., and S.-W. Lee, An analysis of monthly mean wind stress over the global ocean, Mon. Weather Rev., 111, 1554–1566, 1983.
Hanawa, K., P. Rual, R. Bailey, A. Sy, and M. Szabados, A new depth-time equation for Sippican or TSK T-7, T-6, and T-4 expendable bathythermographs (XBT), Deep Sea Res., Part I, 42, 1423–1451, 1995.
Hansen, D. V., and A. Herman, Temporal sampling requirements for surface drifting buoys in the tropical Pacific, J. Atmos. Ocean Technol., 6, 599–607, 1989.
Hansen, D. V., and C. A. Paul, Genesis and effects of long waves in the equatorial Pacific, J. Geophys. Res., 89, 10,431–10,440, 1984.
Hao, Z., and M. Ghil, Data assimilation in a simple tropical ocean model with wind stress errors, J. Phys. Oceanogr., 24, 2111–2128, 1994.
Harrison, D. E., Local and remote forcing of ENSO ocean waveguide response, J. Phys. Oceanogr., 19, 691–695, 1989.
Harrison, D. E., and B. S. Giese, Episodes of westerly winds as observed from islands in the western tropical Pacific, J. Geophys. Res., 96, suppl., 3221–3237, 1991.
Harrison, D. E., and D. S. Luther, Surface winds from tropical Pacific islands: Climatological statistics, J. Clim., 3, 251–271, 1990.
Harrison, D. E., and P. S. Schopf, Kelvin wave induced advection and the onset of SST warming in El Niño events, Mon. Weather Rev., 112, 923–933, 1984.
Harrison, D. E., W. S. Kessler, and B. Giese, Hindcasts of the 1982–83 El Niño: Thermal and dynamic variability along the ship of opportunity XBT tracks, J. Phys. Oceanogr., 19, 397–418, 1989.
Harrison, D. E., B. S. Giese, and E. S. Sarachik, Mechanisms of SST change in the equatorial waveguide during the 1982–83 ENSO, J. Clim., 3, 173–188, 1990.
Hartmann, D. L., H. H. Hendon, and R. A. Houze Jr., Some implications of the mesoscale circulations in tropical cloud clusters for large-scale dynamics and climate, J. Atmos. Sci., 41, 113–121, 1984.
Hayes, S. P., and M. J. McPhaden, Temporal sampling requirements for low frequency temperature variability in the eastern equatorial Pacific Ocean, Tech. Memo. ERL PMEL-96, 17 pp., Natl. Oceanic and Atmos. Admin., Silver Spring, Md., 1992.
Hayes, S. P., et al., The Equatorial Pacific Ocean Climate Studies (EPOCS) Plans: 1986–1988, Eos Trans. AGU, 67, 442–444, 1986.
Hayes, S. P., M. J. McPhaden, and A. Leetmaa, Observational verification of a quasi real-time simulation of the tropical Pacific Ocean, J. Geophys. Res., 94, 2147–2157, 1989a.
Hayes, S. P., M. J. McPhaden, and J. M. Wallace, The influence of sea surface temperature on surface wind in the eastern equatorial Pacific: Weekly to monthly variability, J. Clim., 2, 1500–1506, 1989b.
Hayes, S. P., L. J. Mangum, J. Picaut, A. Sumi, and K. Takeuchi, TOGA TAO: A moored array for real-time measurements in the tropical Pacific Ocean, Bull. Am. Meteorol. Soc., 72, 339–347, 1991a.
Hayes, S. P., P. Chang, and M. J. McPhaden, Variability of the sea surface temperature in the eastern equatorial Pacific during 1986–1988, J. Geophys. Res., 96, 10,553–10,566, 1991b.
Hayes, S. P., L. J. Mangum, and K. E. McTaggart, Repeat CTD measurements along PR16, I, WOCE Notes 3, Tex. A&M Univ., College Station, 1991c.
Hebert, D., J. N. Moum, C. A. Paulson, D. R. Caldwell, T. K. Chereskin, and M. J. McPhaden, Detailed structure of the upper ocean in the central equatorial Pacific during April 1987, J. Geophys. Res., 96, 7127–7136, 1991.
Hellerman, S., and M. Rosenstein, Normal monthly wind stress over the world ocean with error estimates, J. Phys. Oceanogr., 13, 1093–1104, 1983.
Henin, C., and J. Grelet, A merchant ship thermo-salino- graph network in the Pacific Ocean, Deep Sea Res., Part I, 43, 1833–1855, 1996.
Henin, C., Y. du Penhoat, and M. Ioualalen, Observations of sea surface salinity in the western Pacific fresh pool: Large-scale changes in 1992–1995, J. Geophys. Res., in press, 1998.
Hofmann, E. E., The large-scale horizontal structure of the Antarctic Circumpolar Current from FGGE drifters, J. Geophys. Res., 90, 14,004–14,012, 1985.
Horel, J. D., On the annual cycle in the tropical Pacific atmosphere and ocean, Mon. Weather Rev., 110, 1863–1878, 1981.
Horel, J. D., and J. M. Wallace, Planetary scale atmospheric phenomena associated with the Southern Oscillation, Mon. Weather Rev., 109, 813–829, 1981.
Horel, J. D., V. E. Kousky, and M. T. Kagano, Atmospheric conditions in the Atlantic sector, Nature, 322, 248–251, 1986.
Hoskins, B. J., and D. Karoly, The linear steady response of a spherical atmosphere to thermal and orographic forcing, J. Atmos. Sci., 38, 1179–1196, 1981.
Houghton, R. W., The relationship of sea surface temperature to thermocline depth at annual and interannual timescales in the tropical Atlantic Ocean, J. Geophys. Res., 96, 15,173–15,185, 1991.
Houghton, R. W., and Y. Tourre, Characteristics of low-frequency sea surface temperature fluctuations in the tropical Atlantic, J. Clim., 5, 765–771, 1992.
Houze, R. A., Jr., Observed structure of mesoscale convective systems and implications for large-scale heating, Q. J. R. Meteorol. Soc., 115, 425–461, 1989.
Hurlburt, H. E., J. C. Kindle, and J. J. O'Brien, A numerical simulation of the onset of El Niño, J. Phys. Oceanogr., 6, 621–631, 1976.
Integrated Global Ocean Services System (IGOSS), Products bulletin, October–December 1992, report, Bundesampt für Seeschiffahrt und Hydrogr., Hamburg, Germany, 28 pp., 1992.
International Research Institute for Climate Prediction Task Group, International Research Institute for Climate Prediction: A Proposal, 51 pp., Off. of Global Programs, Natl. Oceanic and Atmos. Admin., Silver Spring, Md., 1992.
International TOGA Project Office, Tropical Ocean Global Atmosphere (TOGA) International Implementation Plan, ITPO Rep. 1, World Clim. Res. Programme, World Meteorol. Organ., Geneva, 1992.
Jacobs, G., H. Hurlburt, J. Kindle, E. Metzger, J. Mitchell, W. Teague, and A. Wallcraft, Decade-scale trans-Pacific propagation and warming effects of an El Niño anomaly, Nature, 370, 360–363, 1994.
Ji, M., and A. Leetmaa, Impact of data assimilation on ocean initialization and El Niño prediction, Mon. Weather Rev., 125, 742–753, 1997.
Ji, M., and T. M. Smith, Ocean model responses to temperature data assimilation and varying surface wind stress: Intercomparisons and implications for climate forecast, Mon. Weather Rev., 123, 1811–1821, 1995.
Ji, M., A. Kumar, and A. Leetmaa, An experimental coupled forecast system at the national meteorological center: Some early results, Tellus, Ser. A, 46, 398–418, 1994.
Ji, M., A. Leetmaa, and J. Derber, An ocean analysis system for seasonal to interannual climate studies, Mon. Weather Rev., 123, 460–481, 1995.
Jin, F.-F., J. D. Neelin, and M. Ghil, El Niño on the devil's staircase: Annual subharmonic steps to chaos, Science, 264, 70–72, 1994.
Johnson, E. S., and M. J. McPhaden, On the structure of intraseasonal Kelvin waves in the equatorial Pacific Ocean, J. Phys. Oceanogr., 23, 608–625, 1993a.
Johnson, E. S., and M. J. McPhaden, Effects of a three-dimensional mean flow on intraseasonal Kelvin waves in the equatorial Pacific Ocean, J. Geophys. Res., 98, 10,185–10,194, 1993b.
Jones, C., and C. Gautier, Coupled modes of air-sea interaction and the Madden and Julian Oscillation, paper presented at the TOGA95 Symposium, World Meteorol. Organ., Melbourne, Victoria, Australia, April 2–7, 1995.
Jones, C. S., D. M. Legler, and J. J. O'Brien, Variability of surface fluxes over the Indian Ocean: 1960–1989, Global Atmos. Ocean Syst., 3, 249–272, 1995.
Kalnay, E., et al., The NCEP/NCAR 40-year reanalysis project, Bull. Am. Meteorol. Soc., 77, 437–471, 1996.
Katz, E. J., A. J. Busalacchi, M. Bushnell, F. Gonzalez, L. Gourdeau, M. J. McPhaden, and J. Picaut, A comparison of coincidental time series of the ocean surface height by satellite altimeter, mooring, and inverted echo sounder, J. Geophys. Res., 100, 25,101–25,108, 1995a.
Katz, E. J., J. A. Carton, and A. Chakraborty, Dynamics of the equatorial Atlantic from altimetry, J. Geophys. Res., 100, 25,061–25,068, 1995b.
Keen, R. A., The role of cross-equatorial tropical cyclone pairs in the Southern Oscillation, Mon. Weather Rev., 110, 1405–1416, 1982.
Kessler, W. S., Observations of long Rossby waves in the northern tropical Pacific, J. Geophys. Res., 95, 5183–5218, 1990.
Kessler, W. S., Can reflected extra-equatorial Rossby waves drive ENSO?, J. Phys. Oceanogr., 21, 444–452, 1991.
Kessler, W. S., and J. P. McCreary Jr., The annual wind-driven Rossby wave in the subthermocline equatorial Pacific, J. Phys. Oceanogr., 23, 1192–1207, 1993.
Kessler, W. S., and M. J. McPhaden, The 1991–93 El Niño in the central Pacific, Deep Sea Res., Part II, 42, 295–334, 1995a.
Kessler, W. S., and M. J. McPhaden, Oceanic equatorial waves and the 1991–93 El Niño, J. Clim., 8, 1757–1774, 1995b.
Kessler, W. S., and B. A. Taft, Dynamic heights and zonal geostrophic transports in the central equatorial Pacific during 1979–84, J. Phys. Oceanogr., 17, 97–122, 1987.
Kessler, W. S., M. J. McPhaden, and K. M. Weickmann, Forcing of intraseasonal Kelvin waves in the equatorial Pacific, J. Geophys. Res., 100, 10,613–10,631, 1995.
Kessler, W. S., M. C. Spillane, M. J. McPhaden, and D. E. Harrison, Scales of variability in the equatorial Pacific inferred from the Tropical Atmosphere-Ocean (TAO) array, J. Clim., 9, 2999–3204, 1996.
Kilonsky, B., and P. Caldwell, In the pursuit of high-quality sea level data, IEEE Oceans Proc., 2, 669–675, 1991.
Kindle, J. C., and P. A. Phoebus, The ocean response to operational westerly wind bursts during the 1991–1992 El Niño, J. Geophys. Res., 100, 4893–4920, 1995.
Kleeman, R., A. M. Moore, and N. R. Smith, Assimilation of subsurface thermal data into a simple ocean model for initialization of an intermediate tropical coupled ocean-atmosphere forecast model, Mon. Weather Rev., 123, 3103–3113, 1995.
Knox, R. A., Equatorial response to impulsive wind, in Further Progress in Equatorial Oceanography, edited by E. J. Katz and J. M. Witte, pp. 323–334, Nova Univ. Press, Fort Lauderdale, Fla., 1987.
Knox, R. A., and D. L. T. Anderson, Recent advances in the study of the low-latitude circulation, Prog. Oceanogr., 14, 259–317, 1985.
Knox, R., and D. Halpern, Long range Kelvin wave propagation of transport variations in Pacific Ocean equatorial currents, J. Mar. Res., 40, suppl., 329–339, 1982.
Köberle, C., and S. G. H. Philander, On the processes that control seasonal variations of sea surface temperatures in the tropical Pacific Ocean, Tellus, Ser. A, 46, 481–496, 1994.
Koblinsky, C. J., P. Gaspar, and G. Lagerloef (Eds.), The Future of Spaceborne Altimetry: Oceans and Climate Change, 75 pp., Joint Oceanogr. Inst. Inc., Washington, D.C., 1992.
Koehn, M., L. Mangum, and M. McPhaden (Eds.), Proceedings of the Third Meeting of the TOGA-TAO Implementation Panel, Seoul, Oct. 18–20, 1994, International TOGA Project Office Rep. 12, 61 pp., Pac. Mar. Environ. Lab., Seattle, Wash., 1995.
Koehn, M. P., L. J. Mangum, and M. J. McPhaden (Eds.), Proceedings of the Fourth Workshop of the TAO Implementation Panel, Fortaleza, Brazil, Sept. 12–14, 1995, WCRP Informal Rep. 1/1996, 61 pp., Pac. Mar. Environ. Lab., Seattle, Wash., 1996.
Kumar, A., A. Leetmaa, and M. Ji, Simulations of atmospheric variability induced by sea surface temperatures and implications for global warming, Science, 266, 632–634, 1994.
Kuroda, Y., and M. J. McPhaden, Variability in the western equatorial Pacific Ocean during JAPACS cruises in 1989 and 1990, J. Geophys. Res., 98, 4747–4759, 1993.
Kutsuwada, K., and H. Inaba, Long-range measurement of surface oceanic current in the western equatorial Pacific by acoustic doppler current profiler, J. Meteorol. Soc. Jpn., 73(1), 1–11, 1995.
Latif, M., and T. P. Barnett, Interactions of the tropical oceans, J. Clim., 8, 952–964, 1995.
Latif, M., and N. E. Graham, How much predictive skill is contained in the thermal structure of an oceanic GCM?, J. Phys. Oceanogr., 22, 951–962, 1992.
Latif, M., J. Biercamp, and H. von Storch, The response of a coupled ocean-atmosphere general circulation model to wind bursts, J. Atmos. Sci., 45, 964–979, 1988.
Latif, M., T. P. Barnett, M. A. Cane, M. Fluegel, N. E. Graham, H. von Storch, J.-S. Xu, and S. E. Zebiak, A review of ENSO prediction studies, Clim. Dyn., 9, 167–179, 1994.
Latif, M., R. Kleeman, and C. Eckert, Greenhouse warming, decadal variability, or El Niño: An attempt to understand the anomalous 1990s, J. Clim., 10, 2221–2239, 1997.
Latif, M., D. Anderson, T. Barnett, M. Cane, R. Kleeman, A. Leetmaa, J. O'Brien, A. Rosati, and E. Schneider, A review of the predictability and prediction of ENSO, J. Geophys. Res., this issue.
Lau, K.-M., and A. J. Busalacchi, El Niño Southern Oscillation: A view from space, in Atlas of Satellite Observations Related to Global Change, edited by R. J. Gurney, J. L. Foster, and C. L. Parkinson, pp. 281–294, Cambridge Univ. Press, New York, 1993.
Lau, K.-M., and P. H. Chan, The 40–50 day oscillation and the El Niño/Southern Oscillation: A new perspective, Bull. Am. Meteorol. Soc., 67, 533–534, 1986.
Lau, N.-C., and N. J. Nath, A modeling study of the relative roles of tropical and extratropical SST anomalies in the variability of the global atmosphere-ocean system, J. Clim., 7, 1184–1207, 1994.
Leetmaa, A., and M. Ji, Operational hindcasting of the tropical Pacific, Dyn. Atmos. Oceans, 13, 465–490, 1989.
Leetmaa, A., and M. Ji, Ocean data assimilation as a component of a climate forecast system, in Modern Approaches to Data Assimilation in Ocean Modeling, edited by P. Malanotte-Rizzoli, pp. 271–293, Elsevier, New York, 1996.
Legeckis, R., Long waves in the eastern equatorial Pacific Ocean: A view from a geostationary satellite, Science, 197, 1179–1181, 1977.
Legler, D. M., Producing surface wind products for oceanographers, paper presented at the IGOSS/IOC Ocean Products Workshop, International Oceanographic Commission, Tokyo, April 1991.
Legler, D. M., and J. J. O'Brien, Atlas of Tropical Pacific Wind Stress Climatology 1971–1980, 182 pp., Dep. of Meteorol., Fl. State Univ., Tallahassee, 1984.
Legler, D. M., I. M. Navon, and J. J. O'Brien, Objective analysis of pseudo-stress over the Indian Ocean using a direct-minimisation approach, Mon. Weather Rev., 117, 709–720, 1989.
Lehodey, P., M. Bertignac, J. Hampton, A. Lewis, and J. Picaut, El Niño Southern Oscillation and tuna in the western Pacific, Nature, 389, 715–718, 1997.
Le Traon, P. Y., P. Gaspar, F. Bouyssel, and H. Makhmara, Using TOPEX/POSEIDON data to enhance ERS-1 orbit, J. Atmos. Oceanic Technol., 12, 161–170, 1995.
Levitus, S., and T. P. Boyer, World Ocean Atlas 1994, vol. 4, Temperature, NOAA Atlas NESDIS 4, Washington D.C., 117 pp., Natl. Oceanic and Atmos. Admin., 1994.
Levitus, S., R. Burgett, and T. P. Boyer, World Ocean Atlas 1994, vol. 3, Salinity, NOAA Atlas NESDIS 3, 99 pp., Natl. Oceanic and Atmos. Admin., Washington, D.C., 1994a.
Levitus, S., T. P. Boyer, and J. Antonov, World Ocean Atlas 1994, vol. 5, Interannual Variability of Upper Ocean Thermal Structure, NOAA Atlas NESDIS 5, 176 pp., Natl. Oceanic and Atmos. Admin., Washington, D.C., 1994b.
Li, B., and A. J. Clarke, An examination of some ENSO mechanisms using interannual sea level at the eastern and western equatorial boundaries and the zonally averaged equatorial wind, J. Phys. Oceanogr., 24, 681–690, 1994.
Li, T., and S. G. H. Philander, On the annual cycle of the eastern equatorial Pacific, J. Clim., 9, 2986–2998, 1996.
Lien, R.-C., M. J. McPhaden, and D. Hebert, Intercomparison of ADCP measurements at 0°, 140°W, J. Atmos. Oceanic Technol., 11, 1334–1349, 1994.
Lien, R.-C., D. R. Caldwell, M. C. Gregg, and J. N. Moum, Turbulence variability at the equator in the central Pacific at the beginning of the 1991–1993 El Niño, J. Geophys. Res., 100, 6881–6898, 1995.
Lien, R.-C., M. J. McPhaden, and M. C. Gregg, High-frequency internal waves in the upper central equatorial Pacific and their possible relationship to deep-cycle turbulence, J. Phys. Oceanogr., 26, 581–600, 1996.
Lillibridge, J. L., R. E. Cheney, and N. S. Doyle, The 1991–93 Los Niños from ERS-1 altimetry, in Proceedings of the Second ERS-1 Symposium, Eur. Space Agency Spec. Publ., ESA SP-361, 495–499, 1994.
Lindstrom, E., R. Lukas, R. Fine, E. Firing, S. Godfrey, G. Meyers, and M. Tsuchiya, The Western Equatorial Pacific Ocean Circulation Study, Nature, 330, 533–537, 1987.
Lindzen, R. S., and S. Nigam, On the role of sea surface temperature gradients in forcing low-level winds and convergence in the tropics, J. Atmos. Sci., 44, 2418–2436, 1987.
Liu, W. T., Moisture and latent heat flux variabilities in the tropical Pacific derived from satellite data, J. Geophys. Res., 93, 6749–6760, 1988.
Liu, W. T., and C. Gautier, Thermal forcing of the tropical Pacific from satellite data, J. Geophys. Res., 95, 13,209–13,217, 1990.
Liu, W. T., K. B. Katsaros, and J. A. Businger, Bulk parameterization of air-sea exchanges of heat and water vapor including molecular constraints at the interface, J. Atmos. Sci., 36, 1722–1735, 1979.
Liu, W. T., W. Tang, and R. Atlas, Responses of the tropical Pacific to wind forcing as observed by spaceborne sensors and simulated by an ocean general circulation model, J. Geophys. Res., 101, 16,345–16,359, 1996.
Lorenc, A. C., A global three-dimensional multivariate statistical interpolation scheme, Mon. Weather Rev., 109, 701–721, 1981.
Lu, P., and J. P. McCreary Jr., Influence of the ITCZ on the flow of thermocline water from the subtropical to the equatorial Pacific Ocean, J. Phys. Oceanogr., 25, 3076–3088, 1995.
Lukas, R., and E. Firing, The annual Rossby wave in the central equatorial Pacific Ocean, J. Phys. Oceanogr., 15, 55–67, 1985.
Lukas, R., and E. Lindstrom, The mixed layer in the western equatorial Pacific Ocean, J. Geophys. Res., 96, 3343–3357, 1991.
Lukas, R., P. J. Webster, M. Ji, and A. Leetmaa, The large-scale context for the TOGA Coupled Ocean-Atmosphere Response Experiment, Meteorol. Atmos. Phys., 56, 3–16, 1995.
Luther, D. S., and E. S. Johnson, Eddy energetics in the upper equatorial Pacific during the Hawaii-to-Tahiti Shuttle Experiment, J. Phys. Oceanogr., 20, 913–944, 1990.
Luther, D. S., D. E. Harrison, and R. A. Knox, Zonal winds in the central equatorial Pacific and El Niño, Science, 222, 327–330, 1983.
Madden, R. A., and P. R. Julian, Detection of a 40–50 day oscillation in the zonal wind in the tropical Pacific, J. Atmos. Sci., 28, 702–708, 1971.
Madden, R. A., and P. R. Julian, Description of global-scale circulation cells in the tropics with a 40–50 day period, J. Atmos. Sci., 29, 1109–1123, 1972.
Mangum, L. J., S. P. Hayes, J. M. Toole, Z. Wang, S. Pu, and D. Hu, Thermohaline structure and zonal pressure gradient in the western equatorial Pacific, J. Geophys. Res., 95, 7279–7288, 1990.
Mangum, L. J., S. P. Hayes, and L. D. Stratton, Sampling requirements for the surface wind field over the tropical Pacific Ocean, J. Clim., 9, 668–679, 1992.
Mangum, L. J., H. P. Freitag, and M. J. McPhaden, TOGA-TAO array sampling schemes and sensor evaluations, paper presented at OCEANS 94 OSATES, Institute of Electrical and Electronics Engineers/Ocean Engineering Society, Parc de Penfeld, Brest, France, Sept. 13–16, 1994.
Mantua, N. J., and D. S. Battisti, Evidence for the delayed oscillator mechanism for ENSO: the "observed" oceanic Kelvin mode in the far western Pacific, J. Phys. Oceanogr., 24, 691–699, 1994.
Mapes, B. E., and R. A. Houze Jr., Diabatic divergence profiles in western Pacific mesoscale convective systems, J. Atmos. Sci., 52, 1807–1828, 1995.
Maury, M. F., The Physical Geography of the Sea, Harper Collins, New York, 1859.
May, D. A., M. M. Parmeter, D. S. Olszewski, and B. D. McKenzie, Operational processing of satellite sea surface temperature retrievals at the Naval Oceanographic Office, Bull. Am. Meteorol. Soc., 79, 397–407, 1998.
McCarty, M. E., and M. J. McPhaden, Mean seasonal cycles and interannual variations at 0°, 165°E during 1986–1992, Tech. Memo. ERL PMEL-98, 64 pp., Natl. Oceanic and Atmos. Admin., Silver Spring, Md., 1993.
McClain, E. P., W. G. Pichel, and C. C. Walton, Comparative performance of AVHRR-based multichannel sea surface temperatures, J. Geophys. Res., 90, 11,587–11,601, 1985.
McCreary, J., Eastern tropical ocean response to changing wind systems, with application to El Niño, J. Phys. Oceanogr., 6, 632–645, 1976.
McCreary, J. P., Jr., A linear stratified ocean model of the equatorial undercurrent, Philos. Trans. R. Soc. London A, 298, 603–635, 1980.
McCreary, J. P., Jr., A model of tropical ocean-atmosphere interaction, Mon. Weather Rev., 111, 370–387, 1983.
McCreary, J. P., Jr., and D. L. T. Anderson, An overview of coupled ocean-atmosphere models of El Niño and the Southern Oscillation, J. Geophys. Res., 96, suppl., 3125–3150, 1991.
McCreary, J. P., Jr., and P. Lu, On the interaction between the subtropical and the equatorial oceans: The subtropical cell, J. Phys. Oceanogr., 24, 466–497, 1994.
McCreary, J. P., P. K. Kundu, and R. L. Molinari, A numerical investigation of dynamics, thermodynamics and mixed-layer processes in the Indian Ocean, Prog. Oceanogr., 31, 181–244, 1993.
McPhaden, M. J., Continuously stratified models of the steady-state equatorial ocean, J. Phys. Oceanogr., 11, 337–354, 1981.
McPhaden, M. J., TOGA-TAO and the 1991–93 El Niño-Southern Oscillation event, Oceanography, 6, 36–44, 1993a.
McPhaden, M. J. (Ed.), Proceedings of the First Workshop of the TOGA-TAO Implementation Panel, Joint Institute for Marine and Atmospheric Research, East-West Center, University of Hawaii, Honolulu, Nov. 9–10, 1992, technical report, 26 pp., Joint Institute for Marine and Atmospheric Research, Honolulu, Hawaii, 1993b.
McPhaden, M. J. (Ed.), Proceedings of the Second Workshop of the TOGA-TAO Implementation Panel, Bali, Indonesia, October 18–20, 1993, ITPO Publ. 10, 53 pp., Pac. Mar. Environ. Lab., Seattle, Wash., 1994.
McPhaden, M. J., The Tropical Atmosphere-Ocean array is completed, Bull. Am. Meteorol. Soc., 76, 739–741, 1995.
McPhaden, M. J., Monthly period oscillations in the Pacific North Equatorial Countercurrent, J. Geophys. Res., 101, 6337–6359, 1996.
McPhaden, M. J., and R. A. Fine, A dynamical interpretation of the tritium maximum in the central equatorial Pacific, J. Phys. Oceanogr., 18, 1454–1457, 1988.
McPhaden, M. J., and S. P. Hayes, Moored velocity, temperature and wind measurements in the equatorial Pacific Ocean: A review of scientific results, 1985–1990, paper presented at the International TOGA Scientific Conference, World Clim. Res. Program, Honolulu, Hawaii, July 16–20, 1990a.
McPhaden, M. J., and S. P. Hayes, Variability in the eastern equatorial Pacific during 1986–1988, J. Geophys. Res., 95, 13,195–13,208, 1990b.
McPhaden, M. J., and S. P. Hayes, On the variability of winds, sea surface temperature, and surface layer heat content in the western equatorial Pacific, J. Geophys. Res., 96, suppl., 3331–3342, 1991.
McPhaden, M. J., and M. E. McCarty, Mean seasonal cycles and interannual variations at 0°, 110°W and 0°, 140°W during 1980–1991, Tech. Memo. ERL PMEL-95, 118 pp., Natl. Oceanic and Atmos. Admin., Silver Spring, Md., 1992.
McPhaden, M. J., and H. Peters, Diurnal cycle of internal wave variability in the equatorial Pacific Ocean: Results from moored observations, J. Phys. Oceanogr., 22, 1317–1329, 1992.
McPhaden, M. J., and J. Picaut, El Niño-Southern Oscillation displacements of the western equatorial Pacific warm pool, Science, 250, 1385–1388, 1990.
McPhaden, M. J., and B. A. Taft, Proceedings of the First International TOGA Workshop on Thermal Sampling, Rep. USTOGA-3, 53 pp., Univ. Corp. for Atmos. Res., Boulder, Colo., 1984.
McPhaden, M. J., and B. A. Taft, On the dynamics of seasonal and intraseasonal variability in the eastern equatorial Pacific, J. Phys. Oceanogr., 18, 1713–1732, 1988.
McPhaden, M. J., H. P. Freitag, S. P. Hayes, B. A. Taft, Z. Chen, and K. Wyrtki, The response of the equatorial Pacific Ocean to a westerly wind burst in May 1986, J. Geophys. Res., 93, 10,589–10,603, 1988a.
McPhaden, M. J., A. J. Busalacchi, and J. Picaut, Observations and wind-forced model simulations of the mean seasonal cycle in tropical Pacific sea surface topography, J. Geophys. Res., 93, 8131–8146, 1988b.
McPhaden, M. J., A. J. Busalacchi, and J. Picaut, A model study of potential sampling errors due to data scatter around expendable bathythermograph transects in the tropical Pacific Ocean, J. Geophys. Res., 93, 8119–8130, 1988c.
McPhaden, M. J., S. P. Hayes, L. J. Mangum, and J. M. Toole, Variability in the western equatorial Pacific during the 1986–87 El Niño-Southern Oscillation event, J. Phys. Oceanogr., 20, 190–208, 1990a.
McPhaden, M. J., H. B. Milburn, A. I. Nakamura, and A. J. Shepherd, PROTEUS-Profile Telemetry of Upper Ocean Currents, in Proceedings of the Marine Technology Society Conference, Sept. 25–28, 1990, pp. 353–357, Mar. Technol. Soc., Washington, D.C., 1990b.
McPhaden, M., H. P. Freitag, and A. Shepherd, Moored salinity time series measurements at 0°–140°W, J. Atmos. Oceanic Technol., 7, 568–575, 1990c.
McPhaden, M. J., D. V. Hansen, and P. L. Richardson, A comparison of ship drift, drifting buoy, and current meter mooring velocities in the Pacific South Equatorial Current, J. Geophys. Res., 96, 775–782, 1991.
McPhaden, M. J., F. Bahr, Y. du Penhoat, E. Firing, S. P. Hayes, P. P. Niiler, P. L. Richardson, and J. M. Toole, The response of the western equatorial Pacific Ocean to westerly wind bursts during November 1989 to January 1990, J. Geophys. Res., 97, 14,289–14,303, 1992.
Mechoso, C. R., et al., The seasonal cycle over the tropical Pacific in coupled ocean-atmosphere general circulation models, Mon. Weather Rev., 123, 2825–2838, 1995.
Menkes, C., and A. J. Busalacchi, The impact of TOGA-TAO wind observations on tropical Pacific Ocean simulations, paper presented at the TOGA95 Symposium, World Meteorol. Organ., Melbourne, Victoria, Australia, April 2–7, 1995.
Menkes, C., J.-P. Boulanger, and A. J. Busalacchi, Evaluation of TOPEX and basin-wide Tropical Ocean and Global Atmosphere-Tropical Atmosphere Ocean sea surface topographies and derived geostrophic currents, J. Geophys. Res., 100, 25,087–25,100, 1995.
Meyers, G., Variation of Indonesian throughflow and the El Niño-Southern Oscillation, J. Geophys. Res., 101, 12,255–12,263, 1996.
Meyers, G., and H. Phillips, TOGA XBT sampling strategy, TOGA Notes 7, Oceanogr. Cent., Nova Southeastern Univ., Dania, Fla., 1992.
Meyers, G., J. R. Donguy, and D. Cutchin, Tropical Pacific thermocline topography during 1979–1983, in Papers From 1982/83 El Niño Southern Oscillation Workshop, pp. 33–52, Atl. Oceanogr. and Meteorol. Lab., Miami, Fla., 1983.
Meyers, G., J. R. Donguy, and R. K. Reed, Evaporative cooling of the western equatorial Pacific Ocean by anomalous winds, Nature, 323, 523–526, 1986.
Meyers, G., H. Phillips, N. Smith, and J. Sprintall, Space and time scales for optimal interpolation of temperature-Tropical Pacific Ocean, Prog. Oceanogr., 28, 189–218, 1991.
Meyers, G., R. J. Bailey, and A. P. Worby, Geostrophic transport of Indonesian throughflow, Deep Sea Res., Part I, 42, 1163–1174, 1995.
Milburn, H. B., and P. D. McLain, ATLAS-A low cost satellite data telemetry mooring developed for NOAA's Climate Research Mission, paper presented at the Marine Data Systems International Symposium, Institute of Electrical and Electronics Engineers/Marine Technology Society, New Orleans, La., April 30 to May 2, 1986.
Miller, A. J., R. C. Daniel, T. P. Barnett, N. E. Graham, and J. M. Oberhuber, Interdecadal variability of the Pacific Ocean: Model response to observed heat flux and wind stress anomalies, Clim. Dyn., 9, 287–302, 1994.
Miller, L., and R. E. Cheney, Large-scale meridional transport in the tropical Pacific Ocean during the 1986–1987 El Niño, J. Geophys. Res., 95, 17,905–17,920, 1990.
Miller, L., R. E. Cheney, and B. C. Douglas, Geosat altimeter observations of Kelvin waves and the 1986–87 El Niño, Science, 239, 52–54, 1988.
Miller, R. N., Tropical data assimilation experiments with simulated data: The impact of the Tropical Ocean and Global Atmosphere Thermal Array for the Ocean, J. Geophys. Res., 95, 11,461–11,482, 1990.
Minobe, S., and K. Takeuchi, Annual period equatorial waves in the Pacific Ocean, J. Geophys. Res., 100, 18,379–18,392, 1995.
Mitchum, G., Comparison of TOPEX sea surface heights and tide gauge sea levels, J. Geophys. Res., 99, 24,541–24,554, 1994.
Mitchum, G., and R. Lukas, Westward propagation of annual sea level and wind signals in the western Pacific Ocean, J. Clim., 10, 1102–1110, 1990.
Mitchum, G., B. Kilonsky, and B. Miyamoto, Methods for maintaining a stable datum in a sea level monitoring system, paper presented at OCEANS 94 OSATES, Institute of Electrical and Electronics Engineers/Oceanic Engineering Society, Parc de Penfeld, Brest, France, Sept. 13–16, 1994.
Mizuno, K., B. N. Peter, and T. Watanabe, Observation on subsurface temperature by voluntary ships, in Jpn. Exp. on Asian Monsoon (JEXAM) Annu. Rep., pp. 41–59, Res. and Dev. Bur., Sci. and Technol. Agency, Tokyo, 1995.
Molinari, R. L., and E. Johns, Upper layer temperature structure of the western tropical Atlantic, J. Geophys. Res., 99, 18,225–18,233, 1994.
Molinari, R. L., D. Olson, and G. Reverdin, Surface current distributions in the tropical Indian Ocean derived from compilations of surface buoy trajectories, J. Geophys. Res., 95, 7217–7238, 1990.
Moore, A. M., Aspects of geostrophic adjustment during tropical ocean data assimilation, J. Phys. Oceanogr., 19, 435–461, 1989.
Moore, A. M., Linear equatorial wave mode initialisation in a model of the tropical Pacific Ocean: An initialisation scheme for tropical ocean models, J. Phys. Oceanogr., 20, 423–445, 1990.
Moore, A. M., The role of dynamic adjustment during tropical ocean data assimilation, in Trends in Physical Oceanography, Res. Trends Ser., vol. 1, pp. 1–14, Counc. of Sci. Res. Integration, Trivandrum, India, 1992.
Moore, A. M., and D. L. T. Anderson, The assimilation of XBT data into a layer model of the tropical Pacific Ocean, Dyn. Atmos. Oceans., 13, 441–464, 1989.
Moore, A. M., N. S. Cooper, and D. L. T. Anderson, Initialisation and data assimilation in models of the Indian Ocean, J. Phys. Oceanogr., 17, 1965–1977, 1987.
Moum, J. N., M. J. McPhaden, D. Hebert, H. Peters, C. A. Paulson, and D. R. Caldwell, Internal waves, dynamic instabilities and turbulence in the equatorial thermocline, J. Phys. Oceanogr., 22, 1357–1359, 1992.
Moura, A., and J. Shukla, On the dynamics of droughts in northeast Brazil: Observations, theory, and numerical experiments with a general circulation model, J. Atmos. Sci., 38, 2653–2675, 1981.
Murray, J. W., R. T. Barber, M. R. Roman, M. P. Bacon, and R. A. Feely, Physical and biological controls on carbon cycling in the equatorial Pacific, Science, 266, 58–65, 1994.
Musman, S., Geosat altimeter observations of long waves in the equatorial Atlantic, J. Geophys. Res., 97, 3573–3580, 1992.
Nastrom, G. D., and T. E. VanZandt, Mean vertical motions seen by radar wind profilers, J. Appl. Meteorol., 33, 984–995, 1994.
National Centers for Environmental Prediction, Experimental Long Lead Forecast Bulletin, vol. 5, 54 pp., Nat. Oceanic and Atmos. Admin., Washington, D.C., 1996.
National Research Council, El Niño and the Southern Oscillation: A Scientific Plan, 72 pp., Nat. Acad. of Sci., Washington, D.C., 1983.
National Research Council, U.S. Participation in the TOGA Program: A Research Strategy, 24 pp., Nat. Acad. of Sci., Washington, D.C., 1986.
National Research Council, TOGA: A Review of Progress and Future Opportunities, 51 pp., Nat. Acad. of Sci., Washington, D.C., 1990.
National Research Council, Ocean-Atmosphere Observations for Short-term Climate Predictions, 51 pp., Nat. Acad. of Sci., Washington, D.C., 1994a.
National Research Council, GOALS (Global Ocean-Atmosphere-Land System) for Predicting Seasonal to Interannual Climate, 103 pp., Nat. Acad. of Sci., Washington, D.C., 1994b.
National Research Council, Learning to Predict Climate Variations Associated with El Niño and the Southern Oscillation, 171 pp., Nat. Acad. Sci., Washington, D.C., 1996.
National Weather Service, Experimental Long Lead Forecast Bulletin, 63 pp., Washington, D.C., September 1997.
Nerem, R. S., B. J. Haines, J. Hendricks, J. F. Minster, G. T. Mitchum, and W. B. White, Improved determination of global mean sea level variations using TOPEX/POSEIDON altimeter data, Geophys. Res. Lett., 24, 1331–1334, 1997.
Nicholls, N., Sea surface temperatures and Australian winter rainfall, J. Clim., 2, 965–973, 1989.
Nigam, S., and Y. Chao, Evolution dynamics of tropical ocean-atmosphere annual cycle variability, J. Clim., 9, 3187–3205, 1996.
Niiler, P. P., and J. Paduan, Wind-driven motions in the northeast Pacific as measured by Lagrangian drifters, J. Phys. Oceanogr., 25, 2819–2830, 1995.
Niiler, P. P., R. E. Davis, and H. J. White, Water-following characteristics of a mixed layer drifter, Deep Sea Res., Part A, 34, 1867–1881, 1987.
Niiler, P. P., A. Sybrandy, K. Bi, P. Poulain, and D. Bitterman, Measurements of the water-following capability of Holey-sock and TRISTAR drifters, Deep Sea Res., Part I, 42, 1951–1964, 1995.
Nova University, U.S. TOGA Observing System Mid-Life Progress Review and Recommendations for Continuation, 102 pp., Ft. Lauderdale, Fla., 1989.
Oberhuber, J. M., An atlas based on the COADS data set: The budget of heat, buoyancy and turbulent kinetic energy at the surface of the global ocean, Rep. 15, Max Planck Inst. for Meteorol., Hamburg, Germany, 1988.
Ocean Observing System Development Panel, Scientific Design for the Common Module of the Global Ocean Observing System and the Global Climate Observing System: An Ocean Observing System for Climate, 265 pp., Dep. of Oceanogr., Tex. A&M Univ., College Station, 1995.
Palmer, T. N., C. Brankovic, P. Viterbo, and M. J. Miller, Modeling interannual variations of summer monsoons, J. Clim., 5, 399–407, 1992.
Parsons, D., The integrated sounding system: Description and preliminary observations from TOGA COARE, Bull. Am. Meteorol. Soc., 75, 553–567, 1994.
Pearcy, W. G., and A. Schoener, Changes in the marine biota coincident with the 1982–1983 El Niño in the northeastern subarctic Pacific Ocean, J. Geophys. Res., 92, 14,417–14,248, 1987.
Perigaud, C., Sea level oscillations observed with Geosat along the two shear fronts of the Pacific North Equatorial Countercurrent, J. Geophys. Res., 95, 7239–7248, 1990.
Perigaud, C., and P. Delecluse, Annual sea level variations in the southern tropical Indian Ocean from Geosat and shallow-water simulations, J. Geophys. Res., 97, 20,169–20,178, 1992.
Perigaud, C., and P. Delecluse, Interannual sea level variations in the tropical Indian Ocean from Geosat and shallow-water simulations, J. Phys. Oceanogr., 23, 1916–1934, 1993.
Peters, C. A., V. M. Gerald, P. Woiceshyn, and W. H. Gemmill, Operational processing of ERS-1 scatterometer winds, A documentation, NMC/OPC Tech. Rep. 96, 12 pp., Camp Springs, Md., 1994.
Philander, S. G. H., Equatorial Undercurrent: Measurements and theories, Rev. Geophys., 11, 513–570, 1973.
Philander, S. G. H., Instabilities of zonal equatorial currents, 2, J. Geophys. Res., 83, 3679–3682, 1978.
Philander, S. G. H., Unusual conditions in the tropical Atlantic Ocean in 1984, Nature, 322, 236–238, 1986.
Philander, S. G. H., El Niño, La Niña, and the Southern Oscillation, 293 pp., Academic, San Diego, Calif., 1990.
Philander, S. G. H., and R. C. Pacanowski, The generation of equatorial currents, J. Geophys. Res., 85, 1123–1136, 1980.
Philander, S. G. H., and A. D. Seigel, Simulation of the El Niño of 1982–83, in Coupled Ocean-Atmosphere Models, Elsevier Oceanogr. Ser., vol. 40, edited by J. C. J. Nihoul, pp. 517–542, Elsevier, New York, 1985.
Philander, S. G. H., T. Yamagata, and R. C. Pacanowski, Unstable air-sea interactions in the tropics, J. Atmos. Sci., 41, 604–613, 1984.
Philander, S. G. H., D. Halpern, D. Hansen, R. Legeckis, L. Miller, C. Paul, R. Watts, R. Weisberg, and M. Wimbush, Long waves in the equatorial Pacific Ocean, Eos Trans. AGU, 66, 154, 1985.
Philander, S. G. H., W. J. Hurlin, and R. C. Pacanowski, Properties of long equatorial waves in models of the seasonal cycle in the tropical Atlantic and Pacific Oceans, J. Geophys. Res., 91, 14,207–14,211, 1986.
Philander, S., W. Hurlin, and A. Seigel, A model of the seasonal cycle in the tropical Pacific Ocean, J. Phys. Oceanogr., 17, 1986–2002, 1987.
Phoebus, P. A., and J. S. Goerss, The operational assimilation of SSM/I wind speed data, paper presented at the Ninth Conference on Numerical Weather Prediction, Am. Meteorol. Soc., Denver, Colo., Oct. 14–18, 1991.
Phoebus, P. A., P. A. Wittmann, and J. S. Goerss, Model comparisons depicting the influence of SSM/I wind observations, paper presented at the Seventh Conference on Satellite Meteorology and Oceanography, Am. Meteorol. Soc., Monterey, Calif., June 6–10, 1994.
Picaut, J., and T. Delcroix, Equatorial wave sequence associated with warm pool displacements during the 1986–1989 El Niño-La Niña, J. Geophys. Res., 100, 18,393–18,408, 1995.
Picaut, J., and R. Tournier, Monitoring the 1979–1985 Equatorial Pacific current transports with expendable bathythermography data, J. Geophys. Res., 96, suppl., 3263–3277, 1991.
Picaut, J., S. P. Hayes, and M. J. McPhaden, Use of the geostrophic approximation to estimate time-varying zonal currents at the equator, J. Geophys. Res., 94, 3228–3236, 1989.
Picaut, J., A. J. Busalacchi, M. J. McPhaden, and B. Camusat, Validation of the geostrophic method for estimating zonal currents at the equator from Geosat altimeter data, J. Geophys. Res., 95, 3015–3024, 1990.
Picaut, J., A. J. Busalacchi, M. J. McPhaden, L. Gourdeau, F. I. Gonzalez, and E. Hackert, Open-ocean validation of TOPEX/POSEIDON sea level in the western equatorial Pacific, J. Geophys. Res., 100, 25,109–25,127, 1995.
Picaut, J., M. Ioualalen, C. Menkes, T. Delcroix, and M. J. McPhaden, Mechanisms of the zonal displacements of the Pacific warm pool, Science, 274, 1486–1489, 1996.
Picaut, J., F. Masia, and Y. du Penhoat, An advective-reflective conceptual model for the oscillatory nature of ENSO, Science, 277, 663–666, 1997.
Plimpton, P. E., H. P. Freitag, and M. J. McPhaden, Correcting moored ADCP data for fish-bias errors at 0°, 110°W and 0°, 140°W from 1990 to 1993, NOAA Tech. Memo. ERL PMEL-107, 49 pp., Pac. Mar. Environ. Lab., Seattle, Wash., 1995.
Pugh, D., Tides, Surges, and Mean Sea Level, John Wiley, New York, 1987.
Pullen, P. E., R. L. Bernstein, and D. Halpern, Equatorial long-wave characteristics determined from satellite sea surface temperature and in situ data, J. Geophys. Res., 92, 742–748, 1987.
Puls, C., Oberflächentemperaturen und Strömungsverhältmisse des Aquatorialgürtels des Stillen Ozeans, Dtsch. Arch. Seewarte, 18, 1–38, 1895.
Qiao, L., and R. H. Weisberg, Tropical instability wave kinematics: Observations from the Tropical Instability Wave Experiment (TIWE), J. Geophys. Res., 100, 8677–8694, 1995.
Quinn, W. H., V. T. Neal, and S. E. Antunez de Mayolo, El Niño occurrences over the past four and a half centuries, J. Geophys. Res., 92, 14,449–14,461, 1987.
Ralph, E. A., K. Bi, P. P. Niiler, and Y. du Penhoat, A Lagrangian description of the western equatorial Pacific response to the wind burst of December 1992, J. Clim., 10, 1706–1721, 1997.
Ramanathan, V., and W. Collins, Thermodynamic regulation of ocean warming by cirrus clouds deduced from observations of the 1987 El Niño, Nature, 351, 27–32, 1991.
Ramanathan, V., B. Subasilar, G. J. Zhang, W. Conant, R. D. Cess, J. T. Kiehl, H. Grassl, and L. Shi, Warm pool heat budget and shortwave cloud forcing: A missing physics? Science, 267, 499–503, 1995.
Ramp, S. R., J. L. McClean, C. A. Collins, A. J. Semtner, and K. A. S. Hayes, Observations and modeling of the 1991–1992 El Niño signal off central California, J. Geophys. Res., 102, 5553–5582, 1997.
Rao, R. R., R. L. Molinari, and J. F. Festa, Evolution of the climatological near-surface thermal structure of the tropical Indian Ocean, I, Description of mean monthly mixed layer depth, and sea surface temperature, surface current, and surface meteorological fields, J. Geophys. Res., 94, 10,801–10,815, 1989.
Rao, R. R., R. L. Molinari, and J. F. Festa, Surface meteorological and near surface oceanographic atlas of the tropical Indian Ocean, NOAA Tech. Memo. ERL AOML-69, 59 pp., Atl. Oceanogr. and Meteorol. Lab., Miami, Fla., 1991.
Rasmusson, E. M., and T. H. Carpenter, Variations in tropical sea surface temperature and surface wind fields associated with the Southern Oscillation/El Niño, Mon. Weather Rev., 110, 354–384, 1982.
Rasmusson, E. M., and J. M. Wallace, Meteorological aspects of the El Niño/Southern Oscillation, Science, 222, 1195–1202, 1983.
Rebert, J., J. Donguy, G. Eldin, and K. Wyrtki, Relations between sea level, thermocline depth, heat content, and dynamic height in the tropical Pacific Ocean, J. Geophys. Res., 90, 11,719–11,725, 1985.
Reid, G. C., K. S. Gage, and J. R. McAfee, The thermal response of the tropical atmosphere to variations in equatorial Pacific sea surface temperature, J. Geophys. Res., 94, 14,705–14,716, 1989.
Reverdin, G., P. Delecluse, C. Levi, A. Morliere, and J. M. Verstraete, The near surface tropical Atlantic in 1982–84. Results from a numerical simulation and data analysis, Prog. Oceanogr., 27, 273–340, 1991a.
Reverdin, G., P. Rual, Y. du Penhoat, and Y. Gouriou, Vertical structure of the seasonal cycle in the central equatorial Atlantic Ocean, J. Phys. Oceanogr., 21, 277–291, 1991b.
Reverdin, G., C. Frankignoul, E. Kestenare, and M. J. McPhaden, Seasonal variability in the surface currents of the equatorial Pacific, J. Geophys. Res., 99, 20,323–20,344, 1994.
Reynolds, R. W., A real-time global sea surface temperature analysis, J. Clim., 1, 75–86, 1988.
Reynolds, R. W., Impact of Mount Pinatubo aerosols on satellite-derived sea surface temperatures, J. Clim., 6, 768–774, 1993.
Reynolds, R. W., and D. C. Marsico, An improved real-time global sea surface temperature analysis, J. Clim., 6, 114–119, 1993.
Reynolds, R. W., and T. M. Smith, Improved global sea surface temperature analysis using optimum interpolation, J. Clim., 7, 929–948, 1994.
Reynolds, R. W., and T. M. Smith, A high resolution global sea surface temperature climatology, J. Clim., 8, 1572–1583, 1995.
Reynolds, R. W., K. Arpe, C. Gordon, S. P. Hayes, A. Leetmaa, and M. J. McPhaden, A comparison of tropical Pacific surface wind analyses, J. Clim., 2, 105–111, 1989a.
Reynolds, R. W., C. K. Folland, and D. E. Parker, Biases in satellite derived sea-surface-temperatures, Nature, 341, 728–731, 1989b.
Reynolds, R. R., M. Ji, A. Leetmaa, and D. Halpern, Comparison of effects of different wind stress analyses on tropical Pacific model sea level, paper presented at the TOGA95 International Scientific Symposium, World Meteorol. Organ., Melbourne, Victoria, Australia, April 2–7, 1995.
Richardson, P. L., Eddy kinetic energy in the North Atlantic from surface drifters, J. Geophys. Res., 88, 4355–4367, 1983.
Riddle, A. C., W. M. Angevine, W. L. Ecklund, E. R. Miller, D. B. Parsons, D. A. Carter, and K. S. Gage, In situ and remotely sensed horizontal winds and temperature intercomparisons using integrated sounding systems during TOGA COARE, Contrib. Atmos. Phys., 69, 49–61, 1996.
Roach, D., G. Mitchum, and K. Wyrtki, Length scales of interannual sea level variations along the Pacific margin, J. Phys. Oceanogr., 19, 122–128, 1989.
Roemmich, D., and B. Cornuelle, Digitization and calibration of the expendable bathythermograph, Deep Sea Res., Part A, 34, 299–307, 1987.
Roemmich, D., M. Morris, W. R. Young, and J. R. Donguy, Fresh equatorial jets, J. Phys. Oceanogr., 24, 540–558, 1994.
Rogers, R. R., W. L. Ecklund, D. A. Carter, K. S. Gage, and S. A. Ethier, Research applications of a boundary-layer wind profiler, Bull. Am. Meteorol. Soc., 74, 567–580, 1993.
Ropelewski, C. F., and M. S. Halpert, North American precipitation and temperature patterns associated with the El Niño/Southern Oscillation (ENSO), Mon. Weather Rev., 114, 2352–2362, 1986.
Ropelewski, C. F., and M. Halpert, Global and regional scale precipitation patterns associated with the El Niño/Southern Oscillation, Mon. Weather Rev., 115, 1606–1626, 1987.
Rosati, A., K. Miyakoda, and R. Gudgel, The impact of ocean initial conditions on ENSO forecasting with a coupled model, Mon. Weather Rev., 125, 754–772, 1997.
Rufenach, C., A new relationship between radar cross-section and ocean surface wind speed using ERS-1 scatterometer and buoy measurements, Int. J. Remote Sens., 16, 3629–3647, 1995.
Sadler, J., and B. J. Kilonsky, Deriving surface winds from satellite observations of low-level cloud motions, J. Clim. Appl. Meteorol., 24, 758–769, 1985.
Saha, S., G. White, and R. Reynolds, An evaluation of the surface fluxes in the NMC/NCAR re-analysis, paper presented at the 20th Annual NOAA Climate Diagnostics and Prediction Workshop, Natl. Oceanic and Atmos. Admin., Seattle, Wash., Oct. 23–27, 1995.
Scharoo, R., K. F. Wakker, and G. J. Mets, The orbit determination accuracy of the ERS-1 mission, in Proceedings of the Second ERS-1 Symposium, Eur. Space Agency Spec. Publ., ESA SP-361, 735–740, 1994.
Schopf, P. S., and M. A. Cane, On equatorial dynamics, mixed layer physics, and sea surface temperature, J. Phys. Oceanogr., 13, 917–935, 1983.
Schopf, P. S., and M. J. Suarez, Vacillations in a coupled ocean-atmosphere model, J. Atmos. Sci., 45, 549–566, 1988.
Schubert, S. D., R. B. Rood, and J. Pfaendtner, An assimilated dataset for earth science applications, Bull. Am. Meteorol. Soc., 74, 2331–2342, 1993.
Scientific Committee on Ocean Research (SCOR), Prediction of El Niño, in Proc. 19, pp. 47–51, Sci. Comm. on Ocean Res. Working Group, Paris, 1983.
Servain, J., Simple climatic indices for the tropical Atlantic Ocean and some applications, J. Geophys. Res., 96, 15,137–15,146, 1991.
Servain, J., J. Picaut, P. Lecomte, and M. Seva, A 16-year series of observations of sea surface temperature and wind stress field in the tropical Atlantic, in Time Series of Ocean Measurements, Intergovernmental Oceanogr. Comm. Tech. Ser., vol. 2, pp. 29–32, Intergovernmental Oceanographic Commission, Paris, France, 1984.
Servain, J., J. Picaut, and A. J. Busalacchi, Interannual and seasonal variability of the tropical Atlantic Ocean depicted by sixteen years of sea surface temperature and wind stress, in Coupled Ocean-Atmosphere Models, Elsevier Oceanogr. Ser., vol. 40, edited by J. C. J. Nihoul, pp. 211–237, Elsevier, New York, 1985.
Shaffer, G., O. Pizarro, L. Djurfeldt, S. Salinas, and J. Rutllant, Circulation and low-frequency variability near the Chilean coast: Remotely-forced fluctuations during the 1991–1992 El Niño, J. Phys. Oceanogr., 27, 217–235, 1997.
Sheinbaum, J., and D. L. T. Anderson, Variational assimilation of XBT data, I, J. Phys. Oceanogr., 20, 672–688, 1990a.
Sheinbaum, J., and D. L. T. Anderson, Variational assimilation of XBT data, II, J. Phys. Oceanogr., 20, 689–704, 1990b.
Shriver, J. F., and J. J. O'Brien, Low-frequency variability of the equatorial Pacific Ocean using a new pseudostress dataset: 1930–1989, J. Clim., 8, 2762–2786, 1995.
Shuto, K., Interannual variations of water temperature and salinity along the 137°E meridian, J. Oceanogr., 52, 575–595, 1996.
Smith, N. R., Objective quality controls in an oceanic subsurface thermal analysis scheme, J. Geophys. Res., 96, suppl., 3279–3287, 1991.
Smith, N. R., The BMRC ocean thermal analysis system, Aust. Meteorol. Mag., 44, 93–110, 1995a.
Smith, N. R., An improved system for tropical ocean sub-surface temperature analyses, J. Atmos. Oceanic Technol., 12, 850–870, 1995b.
Smith, N. R., and G. Meyers, An evaluation of expendable bathythermograph and Tropical Atmosphere-Ocean Array data for monitoring tropical ocean variability, J. Geophys. Res., 101, 28,489–28,501, 1996.
Smith, N. R., J. E. Blomley, and G. Meyers, A univariate statistical interpolation scheme for subsurface thermal analyses in the tropical oceans, Prog. Oceanogr., 28, 219–256, 1991.
Smith, T. M., R. W. Reynolds, R. E. Livezey, and D. C. Stokes, Reconstruction of historical sea surface temperatures using empirical orthogonal functions, J. Clim., 9, 1403–1420, 1996.
Smull, B. F., and M. J. McPhaden, Comparison of NCEP/NCAR reanalyzed fields and surface observations over the TOGA-TAO Array, paper presented at the 21st Annual NOAA Climate Diagnostics and Prediction Workshop, Natl. Oceanic and Atmos. Admin., Huntsville, Alabama, October 28 to November 1, 1996.
Soreide, N. N., D. C. McClurg, W. H. Zhu, M. J. McPhaden, D. W. Denbo, and M. W. Renton, World Wide Web access to real-time and historical data from the TAO array of moored buoys in the tropical Pacific Ocean: Updates for 1996, paper presented at OCEANS 96, Mar. Technol. Soc., Fort Lauderdale, Fla., Sept. 23–26, 1996.
Spillane, M., J. Allen, and D. Enfield, Intraseasonal oscillations in sea level along the west coast of the Americas, J. Phys. Oceanogr., 17, 313–325, 1987.
Springer, S. R., M. J. McPhaden, and A. J. Busalacchi, Oceanic heat content variability in the tropical Pacific during the 1982–1983 El Niño, J. Geophys. Res., 95, 22,089–22,101, 1990.
Sprintall, J., and M. J. McPhaden, Surface layer variations observed in multiyear time series measurements from the western equatorial Pacific, J. Geophys. Res., 99, 963–979, 1994.
Sprintall, J., and M. Tomczak, Evidence of the barrier layer in the surface layer of the tropics, J. Geophys. Res., 97, 7305–7316, 1992.
Stockdale, T., D. Anderson, M. Davey, P. Delecluse, A. Kattenberg, Y. Kitamura, M. Latif, and T. Yamagata, Intercomparison of tropical models, Rep. WCRP-79, 37 pp., World Clim. Res. Program, Geneva, 1993.
Stockdale, T. N., A. J. Busalacchi, D. E. Harrison, and R. Seager, Ocean modeling for ENSO, J. Geophys. Res., this issue.
Strauch, R. G., B. L. Weber, A. S. Frisch, C. G. Little, D. A. Merritt, K. P. Moran, and D. C. Welsh, The precision and relative accuracy of profiler wind measurements, J. Atmos. Oceanic Technol., 4, 563–571, 1987.
Stricherz, J., J. J. O'Brien, and D. M. Legler, Atlas of Florida State University Tropical Pacific Winds for TOGA 1966–1985, 275 pp., Fla. State Univ., Tallahassee, 1992.
Stroup, E. D., The thermostad of 13°C water in the equatorial Pacific Ocean, Ph.D. dissertation, 202 pp., Johns Hopkins Univ., Baltimore, Md., 1969.
Sui, C.-H., and K.-M. Lau, Multi-scale phenomena in the tropical atmosphere over the western Pacific, Mon. Weather Rev., 120, 407–430, 1992.
Swenson, M., P. P. Niiler, A. L. Sybrandy, and L. Sombardier, Feasibility of attaching Seacats to TOGA drifter, Ref. Ser. 91–30, Scripps Inst. of Oceanogr., La Jolla, Calif., 1991.
Sy, A., XBT measurements, in WOCE Operations Manual, WHP Operations and Methods, vol. 3.1.3., WOCE Rep. 68/91, pp. 1–19, WOCE Hydrographic Office, Woods Hole, Mass., 1991.
Sybrandy, A. L., and P. P. Niiler, The WOCE/TOGA Lagrangian drifter construction manual, WOCE Rep. 63, Scripps Inst. of Oceanogr., La Jolla, Calif., 1991.
Sybrandy, A., C. Martin, P. Niiler, E. Charpentier, and D. T. Meldrum, WOCE Surface Velocity Programme Barometer Drifter Construction Manual, WOCE Rep. 134/95, Scripps Inst. of Oceanogr., La Jolla, Calif., 1995.
Taft, B. A., and W. S. Kessler, Variations of zonal currents in the central tropical Pacific during 1970 to 1987: Sea level and dynamic height measurements, J. Geophys. Res., 96, 12,599–12,618, 1991.
Tai, C.-K., and J. Kuhn, Orbit and tide error reduction for the first 2 years of TOPEX/POSEIDON data, J. Geophys. Res., 100, 25,353–25,363, 1995.
Tapley, B. D., et al., The Joint Gravity Model 3, J. Geophys. Res, 101, 28,029–28,049, 1996.
Taylor, P. K., The determination of surface fluxes of heat and water by satellite microwave radiometry and in situ measurements, in Large-Scale Oceanography Experiments and Satellites, edited by C. Gautier and M. Fieux, pp. 223–246, D. Reidel, Norwell, Mass., 1984.
Toole, J. M., and M. D. Borges, Observations of horizontal velocities and vertical displacements in the equatorial Pacific Ocean associated with the early stages of the 1982/83 El Niño, J. Phys. Oceanogr., 14, 948–959, 1984.
Tourre, Y. M., and W. B. White, ENSO signals in global upper ocean temperature, J. Phys. Oceanogr., 25, 1317–1332, 1995.
Trenberth, K. E., The definition of El Niño, Bull. Am. Meteor. Soc., 78, 2771–2777, 1997.
Trenberth, K. E., and G. W. Branstator, Issues in establishing causes of the 1988 drought over North America, J. Clim., 5, 159–172, 1992.
Trenberth, K. E., and T. J. Hoar, The 1990–95 El Niño-Southern Oscillation event: Longest on record, Geophys. Res. Lett., 23, 57–60, 1996.
Trenberth, K. E., and J. W. Hurrell, Decadal atmosphere-ocean variations in the Pacific, Clim. Dyn., 9, 303–319, 1994.
Trenberth, K. E., G. W. Branstator, D. Karoly, A. Kumar, N.-C. Lau, and C. Ropelewski, Progress during TOGA in understanding and modeling global teleconnections associated with tropical sea surface temperatures, J. Geophys. Res., this issue.
Tziperman, E., L. Stone, H. Jarosh, and M. A. Cane, El Niño chaos: Overlapping of resonances between the seasonal cycle and the Pacific ocean-atmosphere oscillator, Science, 264, 72–74, 1994.
U.S. TOGA Office, Report of a drafting workshop on elements of a ten-year monitoring component for El Niño and the Southern Oscillation (ENSO), May 11–18, 1983, AOML, Miami, Rep. USTOGA-1, 42 pp., Univ. Corp. for Atmos. Res., Boulder, Colo., 1988.
Waliser, D. E., B. Blanke, J. D. Neelin, and C. Gautier, Shortwave feedbacks and El Niño-Southern Oscillation: Forced ocean and coupled ocean-atmosphere experiments, J. Geophys. Res., 99, 25,109–25,125, 1994.
Walker, G. T., Correlation in seasonal variations of weather IX: A further study of world weather, Mem. Indian Meteorol. Dep., 24, 275–332, 1924.
Wallace, J. M., T. P. Mitchell and C. Deser, The influence of sea-surface temperature on surface wind in the eastern equatorial Pacific: Seasonal and interannual variability, J. Clim., 2, 1492–1499, 1989.
Wallace, J. M., E. M. Rasmusson, T. P. Mitchell, V. E. Kousky, E. S. Sarachik, and H. von Storch, On the structure and evolution of ENSO-related climate variability in the tropical Pacific: Lessons from TOGA, J. Geophys. Res., this issue.
Walton, C. C., Nonlinear multichannel algorithms for estimating sea surface temperature with AVHRR satellite data, J. Appl. Meteorol., 27, 115–124, 1988.
Weare, B. C., Uncertainties in estimates of surface heat fluxes derived from marine reports over the tropical and subtropical oceans, Tellus, Ser. A, 41, 357–370, 1989.
Webster, P. J., and R. Lukas, TOGA COARE: The Coupled-Ocean Atmosphere Response Experiment, Bull. Am. Meteorol. Soc., 73, 1377–1416, 1992.
Webster, P. J., and S. Yang, Monsoon and ENSO: Selectively interactive systems, Q. J. R. Meteorol. Soc., 118, 877–926, 1992.
Webster, P. J., T. N. Palmer, V. O. Magaña, J. Shukla, R. A. Tomas, T. M. Yanai, and A. Yasunari, Monsoon: Processes, predictability, and the prospects for prediction, J. Geophys. Res., this issue.
Weisberg, R. H., and S. P. Hayes, Upper ocean variability on the equator in the Pacific at 170°W, J. Geophys. Res., 100, 20,485–20,498, 1995.
Weisberg, R. H., and C. Wang, Slow variability in the equatorial west-central Pacific in relation to ENSO, J. Climate, 10, 1998–2017, 1997.
Weisberg, R. H., and T. J. Weingartner, Instability waves in the equatorial Atlantic Ocean, J. Phys. Oceanogr., 18, 1641–1657, 1988.
Weller, R. A., and S. P. Anderson, Surface meteorology and air-sea fluxes in the western equatorial Pacific warm pool during TOGA COARE, J. Clim., 9, 1959–1990, 1996.
Weller, R. A., and P. K. Taylor, Surface conditions and surface fluxes OOSDP background, Rep. 3, Tex. A&M Univ., College Station, 1993.
White, W. B., Design of a global observing system for gyre-scale upper ocean temperature variability, Prog. Oceanogr., 36, 169–217, 1995.
White, W. B., and R. G. Peterson, An antarctic circumpolar wave in surface pressure, wind, temperature and sea ice extent, Nature, 380, 699–702, 1996.
White, W. B., and C.-K. Tai, Reflection of interannual Rossby waves at the maritime western boundary of the tropical Pacific, J. Geophys. Res., 97, 14,305–14,322, 1992.
White, W. B., G. Meyers, J. R. Donguy, and S. E. Pazan, Short term climate variability in the thermal structure of the Pacific Ocean during 1979–1982, J. Phys. Oceanogr., 15, 917–935, 1985.
White, W. B., S. E. Pazan, and M. Inoue, Hindcast-forecast of ENSO based upon the redistribution of observed and modeled heat content in the western tropical Pacific, J. Phys. Oceanogr., 17, 264–280, 1987.
Williams, C. R., K. S. Gage, and A. Hollingsworth, A diagnostic study of planetary boundary layer winds observed by the 915 MHz lower tropospheric wind profiler at Christmas Island, in Proceedings of the Seventeenth Climate Diagnostics Workshop, Rep. NTIS-PB94-183895/XAB, pp. 210–215, Natl. Tech. Inf. Serv., Springfield, Va., 1992.
Williams, C. R., W. L. Ecklund, and K. S. Gage, Classification of precipitating clouds in the tropics using 915 MHz wind profilers, J. Atmos. Oceanic Technol., 12, 996–1012, 1995.
Williamson, R. G., and R. S. Nerem, Improved orbit computations for the Geosat mission: Benefits for oceanographic and geodynamic studies (abstract), Eos Trans. AGU, 75(44), Fall Meet. Suppl., 155, 1994.
Woodruff, S. D., R. J. Slutz, R. L. Jenne, and P. Steurer, A comprehensive ocean-atmosphere data set, Bull. Am. Meteorol. Soc., 68, 1239–1250, 1987.
World Climate Research Program, Scientific plan for the Tropical Ocean and Global Atmosphere Program, Tech. Doc. WMO/TD-64, 146 pp., World Meteorol. Organ., Geneva, 1985.
World Climate Research Program, Surface Velocity Programme Planning Committee report of the first meeting, SVP-1, Tech. Doc. WMO/TD-323, World Meteorol. Organ., Geneva, 1988.
World Climate Research Program, JSC/CCCO TOGA Scientific Steering Group, Report of the Ninth Meeting, Kona, Hawaii, 23–25 July, 1990, Tech. Doc. WMO/TD-387, 23 pp., World Meteorol. Organ., Geneva, 1990a.
World Climate Research Program, International TOGA Scientific Conference Proceedings, Honolulu, Hawaii, July 16–20, 1990, Tech. Doc. WMO/TD-379, 239 pp., World Meteorol. Organ., Geneva, 1990b.
World Climate Research Program, TOGA Numerical Experimentation Group, Report of the Seventh Session, La Jolla, Calif., 1–2 November 1994, 8 pp., World Meteorol. Organ., Geneva, 1995a.
World Climate Research Program, CLIVAR, A Study of Climate Variability and Predictability, Tech. Doc. WMO/TD-690, 157 pp., World Meteorol. Organ., Geneva, 1995b.
Wyrtki, K., El Niño-The dynamic response of the equatorial Pacific Ocean to atmospheric forcing, J. Phys. Oceanogr., 5, 572–584, 1975.
Wyrtki, K., Sea level during the 1972 El Niño, J. Phys. Oceanogr., 7, 779–787, 1977.
Wyrtki, K., The response of sea surface topography to the 1976 El Niño, J. Phys. Oceanogr., 9, 1223–1231, 1979.
Wyrtki, K., An estimate of equatorial upwelling in the Pacific, J. Phys. Oceanogr., 11, 1205–1214, 1981.
Wyrtki, K., The slope of sea level along the equator during the 1982/1983 El Niño, J. Geophys. Res., 89, 10,419–10,424, 1984.
Wyrtki, K., Water displacements in the Pacific and the genesis of El Niño cycles, J. Geophys. Res., 90, 7129–7132, 1985a.
Wyrtki, K., Sea level fluctuations in the Pacific during the 1982–83 El Niño, Geophys. Res. Lett., 12, 125–128, 1985b.
Wyrtki, K., Indonesian through flow and the associated pressure gradient, J. Geophys. Res., 92, 12,941–12,946, 1987.
Wyrtki, K., and G. Meyers, The trade wind field over the Pacific Ocean, I, The mean field and the mean annual variation, Rep. HIG-75-1, 26 pp., Univ. of Hawaii, 1975.
Wyrtki, K., and G. Meyers, The trade wind field over the Pacific Ocean, J. Appl. Meteorol., 15, 698–704, 1976.
Wyrtki, K., E. Firing, D. Halpern, R. Knox, G. J. McNally, W. C. Patzert, E. D. Stroup, B. A. Taft, and R. Williams, The Hawaii-to-Tahiti shuttle Experiment, Science, 211, 22–28, 1981.
Xie, S.-P., On the genesis of the equatorial annual cycle, J. Clim., 7, 2008–2013, 1994.
Yu, T. W., and D. G. Deaven, Use of SSM/I wind speed data in NMC's GDAS, paper presented at the Ninth Conference on Numerical Weather Prediction, Am. Meteorol. Soc., Denver, Colo., October 14–18, 1991.
Yu, Z., J. P. McCreary Jr., and J. A. Proehl, Meridional asymmetry and energetics of tropical instability waves, J. Phys. Oceanogr., 25, 2997–3007, 1995.
Yu, Z., P. S. Schopf, and J. P. McCreary Jr., On the annual cycle in the eastern Pacific Ocean, J. Phys. Oceanogr., 27, 309–324, 1997.
Zebiak, S., On the 30–60 day oscillation and the prediction of El Niño, J. Clim., 2, 1381–1387, 1989.
Zebiak, S., Air-sea interaction in the equatorial Atlantic region, J. Clim., 6, 1567–1586, 1993.
Zebiak, S. E., and M. A. Cane, A model of El Niño-Southern Oscillation, Mon. Weather Rev., 115, 2262–2278, 1987.
Zhang, C., Atmospheric intraseasonal variability at the surface in the tropical western Pacific Ocean, J. Atmos. Sci., 53, 739–758, 1996.
Zhang, G. J., On the use of monthly mean data to compute surface turbulent fluxes in the tropical Pacific, J. Clim., 8, 3084–3090, 1995.
Zhang, G. J., and M. J. McPhaden, On the relationship between sea surface temperature and latent heat flux in the equatorial Pacific, J. Clim., 8, 589–605, 1995.
Zhang, G. J., V. Ramanathan, and M. J. McPhaden, Convection evaporation feedback in the equatorial Pacific, J. Clim., 8, 3040–3051, 1995.
Zhang, Y., J. M. Wallace, and D. S. Battisti, ENSO-like interdecadal variability: 1900–1993, J. Clim., 10, 1004–1020, 1997.
Go back to abstract