U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
Variability in the Eastern Equatorial Pacific Ocean During 1986-1988
Michael J. McPhaden and Stanley P. Hayes
NOAA/Pacific Marine Environmental Laboratory, Seattle, Washington
Journal of Geophysical Research, 95(C8), 13,195-13,208 (1990)
Not subject to U.S. copyright. Published in 1990 by the American Geophysical Union.
Appendix A: Data Gaps and Gridding
The depths at which moored velocity and temperature measurements have been
made at 0°, 110°W and 0°, 140°W have changed periodically due to shifting scientific
priorities in EPOCS. Also, although VACM/VMCM temperature and velocity data
return has been high (>90%), occasional instrument failures and the loss
of a mooring at 0°, 110°W between April and October 1982 have led to data gaps.
We have filled these data gaps where appropriate and gridded the time series
to a set of standard levels (Plate 2) to facilitate
the computation of mean seasonal cycles (Appendix B), and the comparison of
the 1982-1983 and 1986-1987 ENSO events (section 6). For example, at 0°, 110°W
we substituted SST as well as temperature and velocity data at 15 m, 50 m, and
100 m from from a backup mooring at 0°, 108°W during April-October 1982; and
we substituted velocity at 80 m from the backup mooring during July-November
1986. We also used linear interpolation between vertically adjacent instruments
and, where this was not possible or advisable, linear extrapolation and/or interpolation
by least squares regression. Some specific examples of these procedures and
how they affect subsequent analyses are presented in this appendix. In each
case the examples are in terms of daily or weekly averaged data; results (quoted
in terms of cross correlations and rms differences) improve with further temporal
averaging. Additional examples are given by McPhaden
et al. [1988]; similarly, Halpern
[1987a] discusses the representativeness of 108°W data as a substitute
for 110°W data for variations with periods longer than 1 week.
At 45 m at 110°W we used a regression fill for zonal velocity during October
1987 to December 1988, because mean zonal velocity curvature precludes linear
interpolation (Figure 4). The regression equation
was based on 3 years (November 1983 to November 1986) of simultaneous measurements
at 25 m and 45 m. The correlation between weekly averaged data and simulated
data derived from this regression fill was 0.95 with a mean (rms) difference
of 0 cm s (15 cm s
(15 cm s ).
We likewise used regression fills for 10-m data based on 25-m or 45-m data at
140°W for March-June 1986, March-May 1987, and May-November 1988. The correlation
of simulated daily 10-m data based on the regression formula with actual daily
data at 10 m for a 4½ year period (April 1983 to October 1987) was 0.94 with
a mean (rms) difference of 0 cm s
).
We likewise used regression fills for 10-m data based on 25-m or 45-m data at
140°W for March-June 1986, March-May 1987, and May-November 1988. The correlation
of simulated daily 10-m data based on the regression formula with actual daily
data at 10 m for a 4½ year period (April 1983 to October 1987) was 0.94 with
a mean (rms) difference of 0 cm s (14 cm
s
(14 cm
s ). Zonal velocity data prior to November
1983 at 110°W were linearly extrapolated based on the underlying vertical shear
from 15 m or 20 m depth to 10 m depth for consistency with the more recent 10-m
time series.
). Zonal velocity data prior to November
1983 at 110°W were linearly extrapolated based on the underlying vertical shear
from 15 m or 20 m depth to 10 m depth for consistency with the more recent 10-m
time series.
The SST time series at 140°W was very gappy, so we have substituted 10-m temperatures
in Figures 2b and B1.
The correlation between 576 contemporaneous daily averaged SST and 10-m temperatures
spanning April 1984 to June 1986 was 0.99 with a mean difference of 0.02°C (10
m colder) and an rms difference of 0.14°C. Thus, for our purposes, 10-m temperatures
are equivalent to SST at 140°W. At 110°W the correspondence between SST and
10- to 20-m temperatures is less perfect because of greater near-surface stratification.
Thus SST data gaps were filled with regression formulae at 110°W using the closest
near-surface temperature record. For instance, several months of missing SST
data between July 1981 and April 1983 were filled with a regression formula
based on 15-m temperatures. The correlation between 233 days of regression-derived
SST data and actual SST data during this period was 0.99 with a mean (rms) difference
of 0.00°C (0.30°C).
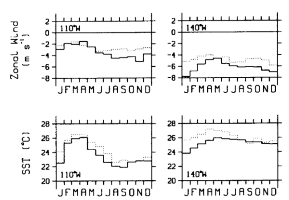
Figure B1. Monthly mean climatologies of sea surface temperature and zonal
winds at 0°, 110°W and 0°, 140°W (solid lines). Superimposed are monthly means
from the Reynolds
[1988] sea surface temperature climatology and Wyrtki
and Meyers [1975] wind climatology (dotted lines).
Temperature time series data were sometimes missing below 200 m (e.g., June-November
1988 at 140°W and February-October 1988 at 110°W). For dynamic height calculations
relative to 250 dbar at these times, we appended the mean temperature gradient
below 200 m to the 200-m temperature record to create an artificial time series
at 250 m. This method, discussed by Kessler
et al. [1985] and McPhaden
et al. [1990a], assumes that temperature changes at depth are
due to vertical displacements of the mean thermal structure. Sensitivity experiments
in which we substituted a mean gradient estimate for existing moored temperature
data at 250 m indicate that the method leads to daily averaged 0-/250-dbar dynamic
height errors of O(0.1 dyn. cm).
Go back to previous section or
forward to next section
PMEL Outstanding Papers
PMEL Publications Search
PMEL Homepage
 (15 cm s
(15 cm s ).
We likewise used regression fills for 10-m data based on 25-m or 45-m data at
140°W for March-June 1986, March-May 1987, and May-November 1988. The correlation
of simulated daily 10-m data based on the regression formula with actual daily
data at 10 m for a 4½ year period (April 1983 to October 1987) was 0.94 with
a mean (rms) difference of 0 cm s
).
We likewise used regression fills for 10-m data based on 25-m or 45-m data at
140°W for March-June 1986, March-May 1987, and May-November 1988. The correlation
of simulated daily 10-m data based on the regression formula with actual daily
data at 10 m for a 4½ year period (April 1983 to October 1987) was 0.94 with
a mean (rms) difference of 0 cm s (14 cm
s
(14 cm
s ). Zonal velocity data prior to November
1983 at 110°W were linearly extrapolated based on the underlying vertical shear
from 15 m or 20 m depth to 10 m depth for consistency with the more recent 10-m
time series.
). Zonal velocity data prior to November
1983 at 110°W were linearly extrapolated based on the underlying vertical shear
from 15 m or 20 m depth to 10 m depth for consistency with the more recent 10-m
time series.