and 55 × 10 N m
at the 110° and 140°W mooring locations, respectively. Sverdrup's
(1947) linear theory of the mean circulation predicts that along the equator,
U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
Time series measurements from surface moored buoys in the eastern equatorial Pacific are analyzed for the period 1983-86. The data, collected as part of the EPOCS and TROPIC HEAT programs, consist of currents, temperatures, and winds on the equator at 110°, 124.5° and 140°W. The purpose is to examine the dynamics of seasonal and intraseasonal variability in the upper 250 m from a diagnosis of the depth integrated zonal momentum (i.e., transport) equation. The principal conclusions of this paper are that 1) there is an approximate balance between mean zonal wind stress and depth integrated pressure gradient; nonlinear advection is significantly nonzero however and leads to an enhancement of eastward transport along the equator; 2) there is an interannual change in zonal wind stress and pressure gradient in which both approximately double over the record length; 3) at the annual cycle, zonal wind stress and depth integrated pressure gradient tend to balance, though the uncertainties are large and other physical processes (e.g., lateral diffusion) are likely to be important; and 4) there exists a very energetic intraseasonal eastward propagating Kelvin-like wave in zonal current, temperature, and dynamic height at periods of 60-90 days which is poorly correlated with the local winds. These waves have amplitudes that are large enough at times to obscure the annual cycle.
The purpose of this paper is to examine the dynamics of seasonal and intraseasonal variability along the equator in the eastern Pacific using time series measurements of wind, current, and temperature from surface moored buoys. We use the term seasonal to include the semi-annual and annual cycles (i.e., periods of 6 to 12 months) and intraseasonal to include frequencies higher than 2 but lower than 12 cycles per year (cpy) (i.e., periods from 1 up to 6 months). The specific questions that we address are: 1) on what time scales is the near surface equatorial Pacific in equilibrium with the local wind stress? and 2) what is the importance of nonlinearity in the dynamics of equatorial current variability? The data were collected from surface moorings at 110°, 124.5°, and 140°W on the equator from October 1983 to May 1986 as part of the TROPIC HEAT Program (Eriksen 1985) and the Equatorial Pacific Ocean Climate Studies (EPOCS) Program (Hayes et al. 1986). The advantages of these data are that 1) they are synoptic, 2) they are finely resolved in time to allow for filtering (rather than aliasing) of high frequency variability in monthly estimates, 3) they span a period of over two years to allow examination of seasonal variations, and 4) they provide direct measurements of currents so that local accelerations and nonlinear advective effects can be estimated.
The paper is organized as follows. Section 2 provides scientific background on the seasonal dynamics of the eastern equatorial Pacific. Section 3 discusses the mooring data and its processing. Section 4 presents time series plots of winds, currents, temperatures, and dynamic heights. Section 5 describes a diagnosis of the depth integrated zonal momentum (i.e., transport) equation. Section 6 is a summary and discussion of the results.
Zonal wind stress in the equatorial Pacific is on average strongest between
about 120° and 160°W (Fig. 1a). This representation
of the wind field, based on 23 years of ship data (Goldenberg
and O'Brien 1981), indicates stress values of 25 × 10
and 55 × 10 N m
at the 110° and 140°W mooring locations, respectively. Sverdrup's
(1947) linear theory of the mean circulation predicts that along the equator,
where P
is depth integrated
pressure gradient and 
is zonal wind stress. For the winds in
Fig. 1a, this leads to a rise in depth integrated pressure
of about 1.5 × 10
N m
between 110° to 140°W (Fig. 1b). The theory also predicts
that zonal transport per unit width (hereafter referred to as transport) should be about
10 m
s along the
equator (Fig. 1c). One would not expect the Sverdrup
balance to be valid at all times and locations however because of the importance of
nonlinearity and planetary scale wave processes.
Figure 1. (a) Mean zonal wind stress (in 10
N m) from 1961-83 from ship wind analyses
(Goldenberg
and O'Brien 1981) using a drag coefficient of 1.2 × 10
and air density of 1.2 kg m; (b) depth integrated
pressure (in 10 N m)
from the Sverdrup
(1947) balance. Values are relative to an arbitrary integration constant
chosen as 5 × 10 N m;
(c) Zonal transport per unit width (in m s)
from the Sverdrup relation. Dashed lines in (c) indicate negative values. Positions
of the current meter moorings are shown by the solid dots at 110°, 124.5° and
140°W.
Philander and Pacanowski (1980) have shown in nonlinear numerical simulations of the Equatorial Undercurrent (EUC) that meridional advection in the thermocline concentrates eastward momentum on the equator, where it is upwelled towards the surface. Similarly, westward momentum put in at the surface by the easterlies is carried poleward in a shallow Ekman layer. This produces a narrower, shallower EUC with larger eastward mass transports relative to linear models (e.g., McPhaden 1981; McCreary 1981). Nonlinear enhancement of eastward transport along the equator can alternately be inferred from the tendency of the flow to conserve absolute vorticity in the presence of an eastward pressure gradient force (e.g., Fofonoff and Montgomery 1955; Cane 1980; Pedlosky 1987).
Nonlinearity in the Pacific EUC has also been examined empirically from velocity section data (Knauss 1966) and several months of moored current meter data (Halpern 1980). These studies indicate that advective terms in the zonal momentum balance may be comparable in magnitude to the zonal pressure gradient. The representativeness of these results is unclear, though, because of the limited data on which they were based.
Ocean current and temperature fields near the equator adjust to wind stress
variations on monthly time scales primarily through the excitation of equatorial
baroclinic Kelvin and long Rossby waves. Adjustment can occur very rapidly relative
to midlatitudes because these waves have O(1 m s)
zonal phase and group speeds. Theory and modeling studies suggest that in a
basin the width of the equatorial Atlantic, wave processes can adjust to ocean
to equilibrium on time scales less than a year (Cane
and Sarachik 1981; Philander
and Pacanowski 1981). This probably accounts for the observational result
that zonal wind stress and pressure gradient nearly balance at the annual period
in the equatorial Atlantic (Katz
et al. 1977, 1986).
There is less agreement on whether the equatorial Pacific should be in equilibrium with winds at the annual cycle. Cane and Sarachik (1981) argued that if the wind forcing were uniform across the basin, the eastern two-thirds of the Pacific should respond in a manner similar to the Atlantic at the annual cycle. Philander (1979) on the other hand suggested that the Pacific would be further from equilibrium than the Atlantic because of its larger zonal extent. Philander and Pacanowski (1981) showed that if significant trade wind variability were confined to a band of meridians--as it is in the equatorial Pacific (e.g., Meyers 1979; Lukas and Firing 1985)--then in the directly forced region the ocean should respond in a succession of steady states at the annual cycle.
Attempts to directly estimate the dynamical response of the equatorial Pacific to fluctuating winds have primarily relied on ship wind and hydrographic data. Mangum and Hayes (1984) and Bryden and Brady (1985) used NORPAX and EPOCS CTD data from 1979-81 to show that in the mean there is a balance between zonal wind stress and pressure gradient along the equator between 110° and 150°W. However, Mangum and Hayes (1984) found near zero correlation between time varying zonal winds and pressure gradients from eight quasi-synoptic pairs of CTD casts at 110° and 150°W. Tsuchiya (1979), on the other hand, used data from the EASTROPAC Expedition in 1967-68 to show that between 95° and 120°W, both easterly wind stress and zonal pressure gradients of comparable magnitude were weak from March to May and strong in June and July. Meyers (1979) computed a mean seasonal cycle of 14°C isotherm depths using mechanical and expendable bathythermograph data and compared variability in isotherm slopes with that seen in climatological winds (Wyrtki and Meyers 1975). In contrast to Tsuchiya (1979), he found that in the eastern and central equatorial Pacific the slope (which was used as a proxy measure of zonal pressure gradient) was weakest in May-June and strongest in October-November, whereas the wind stress was weakest in March-April and strongest in July and December.
The lack of agreement between these studies may be related to aliasing of high frequency energy in both wind and oceanic data. Monthly or quarterly hydrographic measurements along the equator, for example, are not capable of resolving tides (Weisberg et al. 1987), high frequency inertia-gravity waves (Hayes 1981), 20-30 day instability waves (Legeckis et al. 1983), O(10 day) Kelvin wave pulses generated in the western Pacific (Knox and Halpern 1982; Eriksen et al. 1983; McPhaden et al. 1988), or energetic intraseasonal variations at periods of 40-60 days (Enfield 1987). Similarly, infrequent ship wind measurements are subject to large uncertainties due to the presence of pronounced synoptic scale variability in the atmosphere (Luther and Harrison 1984; Halpern 1987d). Better definition of seasonal dynamics thus requires more finely resolved time series measurements that may be filtered to remove high frequency energy.
The data used in this study were collected from taut-wire surface moorings anchored in water 3.7-4.9 km deep (Halpern 1987a). Mooring deployments and recoveries were made approximately every six months for two and a half years (November 1983 to June 1986) on the equator at 108°, 110°, 124.5° and 140°W as part of the TROPIC HEAT and EPOCS programs. Fifteen-minute average currents and temperatures were internally recorded in EG&G; Model 610 Vector Averaging Current Meters (VACM) located at seven depths (10, 25, 45, 80, 120, 160, 250 m) in the upper 250 m at 110°, 124.5° and 140°W. Also, at selected depths between 35 and 200 m, shorter records of temperature sampled every 15 minutes were available. The 108°W mooring was instrumented with three VACMs (at 25, 45 and 80 m) as a backup to the 110°W mooring. Fifteen-minute average vector wind components were also recorded at 110°, 124.5° and 140°W from an inverted VACM equipped with a Climet cup anemometer and vane mounted on the buoy tower 4 m above mean water line. Sea surface temperature (SST) was measured from a thermistor attached to the buoy bridle 1 m below the surface.
Start and end dates of time series used in this study, number of days of data, and ocean depths are summarized in Table 1 for the moorings at 110°, 124.5° and 140°W. Figure 2 shows the mooring array in relation to the thermal structure and dynamic height field along the equator. The moorings span a range of longitudes where the thermocline slopes downward, dynamic height slopes upward, and SST increases from east to west.
Figure 2. Zonal section of temperature and dynamic height (0/250 m dashed and 0/450 m solid) from XBT casts in October 1985 showing mooring positions and VACM depths.
| Longitude | Duration | Ocean depth | ||
|---|---|---|---|---|
| (°W) | Start date | End date | (days) | (m) |
| 100 | 02 Nov 1983 | 30 May 1986 | 941 | 3750 |
| 124.5 | 29 Oct 1983 | 04 Oct 1985 | 707 | 4870 |
| 140 | 20 Oct 1983 | 13 June 1986 | 968 | 4300 |
Overall data return for currents was 97%. The 80 m current record at 110°W
was replaced by the record at 108°W from October 1984-April 1985 due to a failure
of the recorder at 110°W. Coherence is greater than 0.6-0.7 (significant at
the 95% level of confidence) between these two longitudes at periods longer
than 6-7 days (Halpern
1987a), so it is appropriate to make the substitution when examining month-to-month
variability. Data return for subsurface VACM temperatures at each depth was
generally equal to or higher than that for currents. The data return for SST
and winds was lower, being 70% and 79%, respectively. Instrumental errors for
currents, wind, and temperature are O(1 cm s),
O(0.1 m s), and O(0.01°C) (Halpern
1987b, 1987c;
Freitag
et al. 1987) and are not expected to adversely affect our results.
The 15-minute data were block averaged to daily values, examples of which are shown in Fig. 3 for velocity and temperature at selected depths from the 140°W mooring. (Examples of daily time series from 110°W can be found in Halpern 1987a). Also shown are low-pass versions of the time series smoothed with a 51-day Hanning filter (Bendat and Pierson 1971) which effectively eliminates energy at periods shorter than 25 days. The half-amplitude frequency of this filter is 51 days, so that lower frequencies, which are of primary interest in this study, are relatively unattenuated.
Figure 3. Daily averages of (a) zonal velocity (b) meridional velocity, and (c) temperature at 0°N, 140°W at depths of 25 m, 80 m and 160 m. Smooth curves are for daily data smoothed with a 51-day Hanning filter.
Variance preserving spectra of zonal velocity and temperature at 25 m and 80 m (Fig. 4) show increasing energy at periods longer than about 100 days associated with the seasonal cycle. Temperature shows peaks between 60-90 days at all three depths (25, 80 and 160 m) and zonal velocity shows a similar peak at 160 m. There is as much or more zonal velocity variance at periods of 60-90 days in the 25 and 80 m spectra, though it does not appear in the form of a sharp spectral peak as at 160 m. Meridional velocity is dominated by periods shorter than 60 days, e.g., 20-30 day fluctuations associated with instabilities of the large scale zonal currents (e.g., Philander et al. 1985; Halpern 1987a). Unlike zonal velocity and temperature, there are no significant seasonal or 60-90 day oscillations in this variable.
Figure 4. Variance preserving spectra for zonal velocity and temperature shown in Fig. 3 at 0°N, 140°W for daily data. Spectral estimates are based on averages over five adjacent frequency bands. Note that the ordinates are scaled differently at each depth.
Time averaging eliminates high frequency variations that would otherwise be aliased in monthly estimates of zonal velocity and temperature. It will also reduce spatial aliasing in an array of widely spaced moorings to the extent that short period fluctuations are associated with short spatial scales. For example, zonal variability on scales shorter than the mooring separations is evident in Fig. 2. A portion of that variability is associated with 1000 km long instability waves with periods of 20-30 days. Averaging over the period of these waves will simultaneously reduce the energy in the associated wavenumber band.
Results derived from linear least squares analysis of the smoothed data are quoted throughout the text. Data are fit to a six-parameter regression model similar to that presented in McPhaden (1982) for the mean, linear trend, and 1 and 2 cpy harmonics. Error variances are estimated from the residuals about the regression and assume N-M degrees of freedom where M = 6 is the number of regression model parameters and N is the number of months of data. This choice of N is based on the integral time scale (Davis 1976) which is typically about 30 days for residuals. Confidence limits are derived from standard formulae for means, trends, harmonic, sine and cosine functions (Draper and Smith 1966). Confidence limits for harmonic amplitude and phase are based on formulae presented in Jenkins and Watts (1968). As discussed below, errors in stress (due to uncertain drag coefficient), in pressure gradient (due to reference level of 250 m and use of a mean T- S), and in zonal averages of terms in Eq. (3) may be comparable to sampling errors derived from the regression analysis.
Figure 5 shows time series of low passed zonal wind stress at 110°, 124.5° and 140°W from the mooring data. The dashed lines show where data gaps have been filled by an interpolation procedure described in the next section. Meridional winds are not presented since they are generally weaker (e.g., Halpern 1987a), relatively ineffective at exciting low-frequency variability (e.g., Gent et al. 1983), and do not enter into the zonal momentum balance which will be diagnosed in the next section.
Figure 5. Zonal wind stress data at the mooring sites smoothed with a 51-day Hanning filter. Dashed lines are data interpolated according to a procedure outlined in section 5.
Wind stress has been calculated from daily averaged data using a methodology
outlined in Large
and Pond (1982), then smoothed with a 51-day Hanning filter. A constant
stress, neutrally stable boundary layer has been assumed and the 4 m winds extrapolated
to 10 m for incorporation into the bulk formula. The drag coefficient and air
density are set at 1.2 × 10 and 1.2 kg m,
respectively. Uncertainty in the wind stress is mainly due to imprecise knowledge
of the drag coefficient, which can lead to bias errors of 20%. For typical trade-wind
speeds, this is equivalent to an error of O(10
N m).
Concentrating on uninterpolated data (solid curves) in Fig.
5, one notes a clearly defined seasonal minimum in boreal spring at all
three longitudes. At 140°W, seasonal maxima occur from November to January consistent
with Meyers'
(1979) climatological analysis. At 110°W in 1985, a strong August-September
maximum occurs but no maximum in the subsequent fall-winter. Wind stress generally
increases from east to west, with a mean of about 25 × 10
N m at 110°W to 70 × 10
N m at 140°W, values which are comparable
to the climatological means (Fig. 1). Variability
also increases westward and is dominated by the 1 cycle per year harmonic which
has an amplitude of about 15 × 10 N m
at 110°W and 25 × 10 N m
at 140°W. We also note in Fig. 5 that there is
a tendency for easterly stress to be stronger in 1985-86 relative to 1983-84.
Figure 6 displays times series of smoothed zonal velocity at 110° and 140°W for the period November 1983-May 1986. Data from 124.5°W are not shown, since they are not greatly different in character.
Figure 6. Equatorial current and transport time series smoothed with a 51-day
Hanning filter at (a) 110°W and (b) 140°W. Dashed contours indicate westward flow; cross
hatching indicates eastward flow >100 cm s. Means
calculated from a six-parameter regression analysis (see section 3) are shown on the
right. Total (eastward) transport per unit width in the upper 250 m is indicated by the
solid (dashed) line.
Figures 2 and 6 show that
the Equatorial Undercurrent is found in the upper thermocline which shoals from west to
east. Maximum mean speeds are 107 cm s at 120 m
(140°W) and 88 cm s at 80 m (110°W). Mean westward
speeds in the South Equatorial Current (SEC) at 10 m are 12 cm s (140°W) and 4 cm s
(110°W).
The EUC core undergoes an annual migration in depth at both longitudes. At 110°W the core migrates from about 50 m in the boreal spring when EUC speeds are largest, to 80 m in the fall when speeds are weakest (Fig. 6a); at 140°W, similar vertical excursions occur between about 80 and 120 m (Fig. 6b). Variability above the core is dominated by the annual cycle which diminishes rapidly below 100 m (see also Halpern 1987a). Eastward flow near the surface occurs in boreal spring, a phenomenon documented nearly a century ago from analysis of ship-drift data (Puls 1895). Strong westward flow in the South Equatorial Current (SEC) and weak eastward flow in the EUC occur in boreal summer and fall.
Currents in Fig. 6 also show a pronounced oscillation at
periods of 60-90 days below the EUC core at both longitudes, with typical peak-to-peak
amplitudes of about 20 cm s . There is energy at 60-90
day periods above the EUC core as well (q.v., the spectra in Fig.
4), though in the time series it is obscured by the more energetic annual cycle. No
similar fluctuation is obvious in either the winds (Fig. 5)
or meridional velocity (Fig. 3b).
Figure 7 shows in general significantly nonzero correlation with 90% or greater confidence for zonal currents between 110° and 140°W. At 25 m where the annual cycle is prominent, currents at 110°W are most highly correlated with those at 140°W 14 days later, suggesting westward phase propagation. The uncertainty in the magnitude of this phase lag is large however, as it is for the more closely spaced station pairs 110°/124°W and 124°/140°W. On the other hand, the westward direction of phase propagation may be significant since all the correlation functions at 25 m are skewed toward positive lags.
Figure 7. Cross-correlation analyses for zonal currents at 25 and 160 m depth between 110°-124.5°W, 110°-140°W and 124.5°-140°W. Data have been demeaned and detrended. Maximum correlation (r) and corresponding lag in days is shown in upper left of each panel. Positive (negative) lag means that the second time series lags (leads) the first. Heavy tick marks indicate 90% confidence limits for the null hypothesis calculated using the integral time scale to estimate degrees of freedom (Davis 1976). Integral time scale is based on correlation calculations for lags up to ±2 years and is about 5-6 months at 25 m and 1-2 months at 160 m; only lags to ±180 days are plotted for brevity.
Figure 7 shows eastward progression of the 60-90
day velocity signal at 160 m (representative of the depth range 120-250 m) in
contrast to the apparent westward progression of the annual cycle above the
EUC core. The 160 m currents at 110°W lag those at 124° and 140°W by 11 and
18 days respectively, and currents at 124.5°W lag those at 140°W by 9 days.
Thus, the signal propagates eastward at an average speed of 214 cm s
between 140° and 110°W, with slightly higher speeds between 140° and 124.5°W
(221 cm s) and lower speeds between 124°
and 110°W (169 cm s). The uncertainty in
these phase speed estimates is about 20% based on a series of calculations taking
three one-year overlapping segments of data at each of the three zonal separations
and computing lags at maximum cross-correlation. Thus, these phase speeds cannot
be statistically distinguished from those of first baroclinic mode Kelvin waves,
which would have speeds of 246 cm s at 150°W
(Rothstein
1984) and 210 cm s at 110°W (Hayes
and Halpern 1984), respectively. However, they are generally higher than
the corresponding second mode speeds of 146 cm s
(150°W) and 130 cm s (110°W). The zonal
wavelength, estimated by assuming a period of 75 days and a phase speed of 210
cm s , is approximately 120 degrees of longitude,
which is comparable to the width of the equatorial Pacific!
Zonal transport per unit width in the upper 250 m, shown in the upper panels of Fig. 6a and 6b, is on average
105 m s at 110°W and
138 m s at 140°W.
Total transport is nearly identical to the eastward transport of the EUC because the
surface SEC, when present, is generally weaker than 50 cm s and shallower than 50 m. The total transport is also an
order of magnitude larger than the 10 m s predicted by the Sverdrup calculation (Fig. 1c). Part of the discrepancy is due to the shallow depth
range of the mooring data, although as will be shown in section 5, most of the Sverdrup
pressure signal, and presumably therefore transport signal, is found in the upper 250 m.
Zonal transport exhibits an annual variation which is consistent with the current
variations in the upper 100 m. Like the winds, it has increasing amplitude towards the
west (31 m s at
110°W versus 44 m s
at 140°W). Phase also increases towards the west with 110°W leading 140°W by 19 days,
which though highly uncertain, is comparable to the 14-day lead inferred from the 25-m
cross-correlation analysis.
Figure 8 shows isotherm depths and sea surface temperature (SST) at 110° and 140°W. Temperature at 10 m has also been plotted to provide an indicator of SST variability across gaps in the SST record. Mean SST is warmer by 1.9°C at 140°W (25.0°C) than at 110°W (23.1°C). At both locations a well-defined annual cycle is seen which is consistent in amplitude and phase with Horel's (1982) analysis of historical data. The mean position of the upper thermocline, roughly delineated by the 15°-20°C isotherms, is deeper by about 50 m at 140°W compared to 110°W. Annual variations in thermocline depth at both locations are weak and tend to be obscured by O(10 m) depth coherent fluctuations at periods of 60-90 days. These intraseasonal fluctuations are generally more pronounced at 140°W than at 110°W, especially in late 1984 and early 1985. Cross-correlation analysis in the thermocline at 110°, 124.5° and 140°W indicates that the oscillations propagate eastward with phase speeds similar to those inferred from the velocity cross-correlation at 160 m. Moreover, zonal currents and temperature variations are nearly in phase at periods of 60-90 days as indicated by the velocity and temperature cross-correlation at 160 m (Fig. 9). This phase relationship is consistent with an equatorial Kelvin wave origin for the observed variability.
Figure 8. Time series of isotherm depths and SST smoothed with a 51-day Hanning filter at (a) 110°W and (b) 140°W. Means calculated from a six-parameter regression analysis (see section 3) are shown on the right.
Figure 9. Cross-correlation analyses of currents and temperature at 110°, 124.5° and 140°W from a depth of 160 m. Positive (negative) lags imply that temperature leads (lags) zonal velocity. Format is otherwise as in Fig. 7.
Figure 8b shows an interannual deepening of the thermocline at 140°W by 30-40 m from late 1983 to late 1985. Interannual changes in SST and 10 m temperatures are also evident; both were cooler in late 1983 compared to late 1985 by about 1°C at 140°W and by about 2°C at 110°W. Our regression fit to these temperature data indicates linear trends significantly nonzero with 95% or greater confidence. This is consistent with the analysis of Wyrtki (1984) and Kessler and Taft (1987) who found that the eastern and central equatorial Pacific were unusually cool after the 1982-83 El Niño.
Dynamic height has been calculated from observed temperatures and a mean T-S relationship for each of the mooring sites. The T-S curves are derived from an ensemble of about ten EPOCS CTD casts. With the exception of El Niño periods, when low surface salinities can lead to large positive biases, the error involved in estimating dynamic height in this manner is random and about 2 dyn cm in magnitude (Kessler and Taft 1987).
Our temperature measurements to 250 m should capture much of the signal in near surface dynamic height along the equator. For example, zonal dynamic height gradients at the surface relative to 250 m are visually indistinguishable from those relative to 450 m for the October 1984 XBT section shown in Fig. 2. Moreover, Mangum and Hayes (1984) observed that below 200 m, the mean dynamic height difference relative to 1000 db between 110° and 150°W was about 1 dyn cm, which was not statistically different from zero at the 95% level of confidence. However, they noted that the time variability in dynamic height has a deep signature which could be due to low baroclinic mode waves. Kessler et al. (1985) showed that 0/200 m dynamic height estimates contain about 52% of the variance (i.e., 72% of the amplitude) of 0/1000 m dynamic height estimates as determined from Hawaii-Tahiti Shuttle CTD data. Thus, we expect that our 250 m reference level will lead to relatively small errors in estimates of mean dynamic height gradients; however, the amplitude of dynamic height fluctuations calculated relative to 250 m may be too low by as much as 25%-30%.
Figure 10 shows dynamic heights relative to 250 m at
110° and 140°W. In the mean, surface dynamic height is 17 dyn cm higher at 140°W than
at 110°W. For comparison with Sverdrup pressure, depth integrated dynamic height
increases by about 1.4 × 10 N m from 110° to 140°W, comparable to values in Fig. 1b. Variability is greater at 140°W than at 110°W at
all depths above 250 m, and, as expected from the temperature data in Fig. 8, the annual cycle is relatively weak, e.g., 1.5 dyn cm
at 110°W and 2.5 dyn cm at 140°W for 1 cpy surface height amplitudes. The trend at
140°W towards higher dynamic heights is associated with the deepening thermocline (Fig. 8b) and is significant at the 99% level of confidence.
Figure 10. Dynamic height variations relative to 250 m smoothed with a 51-day Hanning filter at (a) 110°W and (b) 140°W. Means calculated from a six-parameter regression analysis are shown on the right.
As with temperature, the 60-90 day periodicity is very prominent in the dynamic height time series. At the surface this oscillation has peak-to-peak amplitudes of about 10 dyn cm at 140°W, as compared with about 4 dyn cm at 110°W. It is most pronounced and regular at 140°W during the second half of 1984 and early 1985, and least well developed over the first 6 months of record. Like temperature, variability in dynamic height propagates eastward nearly in phase with zonal velocity at periods of 60-90 days.
In this section we examine the dynamics of month-to-month variations described above through a diagnosis of the zonal momentum equation.
We can write the zonal momentum equation as
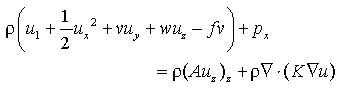(1)
where u, v and w are zonal, meridional and vertical velocity
components, p is pressure, 
(= 10
kg m) is density, f is the Coriolis
parameter, A is vertical eddy viscosity and K is horizontal eddy
viscosity. Subscripts denote differentiation and the operator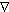 
is a horizontal gradient operator. We can neglect the Coriolis term on the equator
since f = 0 there. Horizontal diffusion will also be neglected because
even though it may be important (e.g., Hansen and Paul 1984; Bryden et al. 1986),
it cannot be estimated from only equatorial data.
Theory indicates that meridional advection of momentum is likely to be important
in the dynamics of the Undercurrent (see section 2 and Philander
and Pacanowski 1980). We would expect therefore that the term vu
will be significantly nonzero in the latitudinally sheared zone of the EUC north
and south of the equator. This term can also be large near the surface where
meridional winds can produce significant cross-equatorial flows (e.g., Cane
1979). However, at the depth of the EUC on the equator, vu
will be locally small relative to the pressure gradient since on seasonal time
scales meridional velocity variations are typically only O(1 cm s)
(e.g., Fig. 3) and u
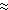0 by symmetry (Lukas
and Firing 1984). Hence, we neglect vu
in (1).
The vertical diffusion term is not easily estimated from our data because 1) the eddy viscosity is highly variable with depth and precisely known (e.g., Peters et al. 1988) and 2) second derivatives of u would be very noisy computed from data at only seven depths. However, integrating from 0 m to 250 m, we get
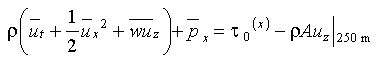(2)
where the overbar denotes depth integral, e.g.,
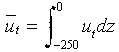
and
is the zonal wind stress. For consistency with pressure and stress integrals,
10 m velocity data are first linearly extrapolated to the surface. Differences
between velocity integrals to 0 m and to 10 m are only a few percent, however,
so our results are insensitive to the choice of upper bound. Equation (2), which
governs zonal transport variability, now requires an estimate of A at
only one depth (250 m) and an estimate of zonal velocity shear instead of curvature.
We have data from discrete times and depths at the mooring locations from which to calculate terms in (2). We therefore use finite differences in time to estimate acceleration and in depth to estimate vertical shear. We also use finite differences in the zonal direction to estimate the zonal pressure gradient and the zonal advection. To compare two-point zonal gradient estimates of velocity and pressure with other terms in (2), we average zonally to get
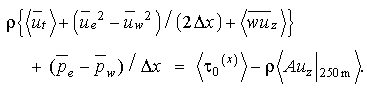(3)
The angle brackets denote zonal average, e.g.,
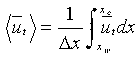
where x
and x
are eastern and western longitudes and 
x
= x - x.
For convenience, we will designate the three intervals of 110°-124.5°W, 124.5°-140°W
and 110°-140°W as 117°, 132° and 125°W, respectively.
Averaging zonal velocity across 15° and 30° of longitude is reasonable given
the high correlations noted for between 110° and 140°W in the previous section.
However, there is an error involved in estimating averages in (3) across an
interval (x, x)
using data from just the end points (Bryden
1977). As an extreme example of how this can affect our results, consider
the 60-90 day wave for which one quarter wavelength fits between 110°and 140°W.
Using Bryden's formulae for a pure progressive sine wave, averages in the angle
brackets would be too low by about 20% relative to the true average. For less
extreme variations across the array, as for example 1/10 to 1/20 of a cycle
in transport at 1 cpy, estimates of average amplitude would be reduced by 10%
or less. Average gradients, i.e. (
- )/(2
x), are exact.
Zonally averaging zonal wind stress for use in (3) poses a problem because of the large data gaps in the records at each longitude. However, one can see from the solid curves in Fig. 5 that there is a high correlation between records at adjacent mooring sites. Between 110° and 124°W this correlation is 0.96 for 14 monthly mean pairs; and between 124° and 140°W it is 0.94 for 8 monthly mean pairs. Hence, we can use regression analysis based on adjacent locations to fill record gaps for improved zonal averages. These regression fills are shown in Fig. 5 by the dashed lines. Fills were made only for "nearest neighbor" sites since the very tight regression weakens over 30 degrees of longitude to 0.63 between 100° and 140°W.
The nonlinear term ½u
has been calculated by first forming products of daily data, then smoothing
with the 51-day Hanning filter. Vertical velocity is too weak to measure directly
and we have no reliable way of estimating it from our data. We attempt calculation
of time mean vertical advection in (3) though, using an estimate of w
from Bryden
and Brady's (1985) diagnostic model of the steady equatorial circulation
in the region 110° to 150°W. This mean velocity (their Fig.
7) has a maximum upwelling of about 3 × 10
cm s at 60 m, crosses zero at about 180
m and shows downwelling at a rate of 1 × 10
cm s at 250 m. Vertical velocity profiles
similar in magnitude and structure have been estimated from mooring data in
the equatorial Pacific at 110°W (Halpern
and Freitag 1987) and between 110°-150°W (Bryden
et al. 1986).
Figure 11 shows examples of pressure gradient, local acceleration, and zonal advection before integration over depth for the interval centered at 125°W. Also shown in Fig. 11c is our estimated profile of time mean vertical advection. It is interesting to note that the mean profiles in Figs. 11a and 11c are quantitatively and qualitatively similar to profiles from Bryden and Brady's (1985) diagnostic model of the mean circulation between 110° and 150°W. Their results were based solely on hydrographic data in contrast to ours which are based principally on time series measurements.
Figure 11. Time series estimates of (a) zonal pressure gradient, p,
relative to 250 m, (b) local acceleration, u
,
and (c) zonal advection, ½u
for the interval centered at 125°W. Contour interval is 1.0 × 10
N m, though the ±0.5 × 10
N m contour is also drawn. Means are estimated
from a 6-parameter regression fit. Dashed line in the mean panel of (c) is the
vertical advection term WU
.
Zonal pressure gradient fluctuations (Fig. 11a)
are vertically coherent with largest amplitudes of O(10
N m) in the upper 100 m, decreasing to zero
at the 250 m reference level. The gradient is always negative with seasonal
minima in boreal spring of each year. However, 60-90 day waves tend to obscure
seasonal variations, especially in the latter part of 1984. A distinct interannual
increase in the gradient is seen between 1983-84 and 1985-86.
Fluctuations in local acceleration of O(10
N m) (Fig. 11b)
are comparable to those of the pressure gradient. The 60-90 day periodicity
is dominant and tends to be vertically coherent as for the pressure gradient.
There is no obvious evidence of a seasonal variation in U;
nor are there trends in velocity over the record length as indicated by the
near zero mean of acceleration.
Zonal advection changes sign at the approximate depth of the EUC core and is
comparable to or larger than the pressure gradient below about 100 m (Fig.
11c). It exhibits an annual cycle between 50-100 m which reflects vertical
movement of the EUC core across these depths (Fig.
6). Also evident is variability at 60-90 day periods of O(10
N m) in the upper 250 m, as for zonal pressure
gradient and local acceleration.
Mean zonal and vertical advection tend to oppose one another above and below the EUC core (Fig. 11c), consistent with the fact that the EUC shoals towards the east. The tendency for the two terms to cancel suggests that nonlinearity on the zonal plane is important in redistributing momentum in the upper 250 m. However, the cancellation is not complete since near the surface there is a large mean upward advection of eastward momentum from the depth of the EUC core. This leads to a reduction of westward flow at the surface and a large zonal transport along the equator relative to that expected from linear theory (q.v., Philander and Pacanowski 1980).
Figure 12 shows estimates of the terms in the depth integrated momentum balance (3) for the intervals centered at 117°, 125° and 132°W. For convenience we write (3) in a simplified notation given by
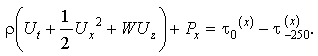(3')
Record gaps in the wind stress time series indicate when zonally averaged stress could not be calculated with at least 50% observed data based on the solid curves in Fig. 5. Thus for example, we did not estimate averaged stress in late 1984 and early 1985 across the intervals centered at 117° or 125°W. Overplotted smooth lines are reconstituted time series based on the mean, trend, and 1 cpy harmonics from the regression analyses (Tables 2, 3). The 2 cpy was not included because, except for the zonal winds, this harmonic was generally insignificant.
Figure 12. Estimates (in N m) of terms
in (3) for the intervals centered at (a) 117°, (b) 125° and (c) 132°W. Shown
in the uppermost panel at each location is ten times the vertical shear stress
at 250 m. Also shown as dotted and long dashed lines are time series reconstituted
from the least squares determined trend, mean, and 1 cpy variations.
| Longitude | ||||||
|---|---|---|---|---|---|---|
| (°W) | Dates | |
P |
U |
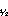U |
WU |
| 117 | Nov 83–Nov 84 | –24.1 ± 1.8 | –21.9 ± 3.9 | X | X | X |
| 117 | May 84–Sep 85 | X | –27.2 ± 3.4 | (–0.3 ± 7.0) | –5.7 ± 0.9 | –13.2 |
| 125 | Nov 83–Nov 84 | –29.5 ± 2.1 | –28.7 ± 3.1 | (–2.3 ± 6.7) | –7.8 ± 2.6 | –16.1 |
| 125 | June 85–May 86 | –55.5 ± 3.6 | –49.1 ± 4.3 | (0.7 ± 9.8) | –4.9 ± 2.0 | –17.8 |
| 132 | Nov 83–Nov 84 | –34.4 ± 2.5 | –34.3 ± 3.9 | X | X | X |
| 132 | May 84–Sep 85 | –64.3 ± 2.1 | –52.8 ± 4.8 | (0.5 ± 6.5) | –3.2 ± 1.1 | –22.5 |
| Longitude | Dates | |
P |
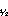U |
U |
|---|---|---|---|---|---|
| 117 | Nov 83–Nov 84 | ||||
| Amplitude | 12.0 ± 3.5 | 14.0 ± 9.9 | X | X | |
| Phase | 113 ± 29 | 97 ± 47 | X | X | |
| 117 | May 84–Sep 85 | ||||
| Amplitude | X | 8.8 ± 5.1 | (7.8 ± 9.7) | (1.1 ± 1.4) | |
| Phase | X | 99 ± 31 | (41 ± 80) | (251 ± 72) | |
| 125 | Nov 83–Nov 84 | ||||
| Amplitude | 13.7 ± 3.8 | 13.2 ± 8.6 | (6.9 ± 23.7) | (2.6 ± 5.9) | |
| Phase | 115 ± 29 | 89 ± 36 | (45 ± 85) | (289 ± 178) | |
| 125 | June 85–May 86 | ||||
| Amplitude | 19.9 ± 9.7 | 11.6 ± 11.2 | (13.9 ± 37.5) | (3.2 ± 6.5) | |
| Phase | 98 ± 34 | 100 ± 71 | (50 ± 62) | (262 ± 89) | |
| 132 | Nov 83–Nov 84 | ||||
| Amplitude | 15.1 ± 4.7 | 14.4 ± 11.9 | X | X | |
| Phase | 120 ± 33 | 76 ± 37 | X | X | |
| 132 | May 84–Sep 85 | ||||
| Amplitude | 24.2 ± 3.0 | (5.0 ± 7.2) | (8.5 ± 9.1) | 1.6 ± 1.5 | |
| Phase | 149 ± 7 | (133 ± 79) | (44 ± 67) | 36 ± 60 | |
Shown in the uppermost frame at each location is ten times the averaged zonal
shear stress at 250 m calculated using an eddy viscosity of A = 10
m s. This
choice of A is based on recent microstructure measurements in the thermocline
of the eastern equatorial Pacific (Peters
et al. 1988). Though subject to considerable uncertainty and derived from
data no deeper than 140 m, this value of A leads to estimates of stress
at 250 m that are 100 times smaller than at the surface. Thus, we will neglect
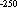in subsequent discussion since it is unlikely to affect our conclusions.
To examine the relationship between zonal wind stress and pressure gradient,
we first subsampled the time series every 31 days, then generated scatter diagrams
and linear regression fits for the intervals centered at 117°, 125° and 132°W
(Fig. 13). The correlation between stress and
gradient is positive in all three intervals and is >0.80 at 132° and 125°W.
The slope of the regression lines in these latter two intervals indicates that
on a month-to-month basis,
is 10%-20% larger than P.
The inequality could be due to a combination of the shallow 250 m reference
level for P , uncertainty
in the wind stress drag coefficient, and the importance of nonlinearity. The
lower correlation between P
and
in the interval centered at 117°W vis-a-vis 132°W may reflect the fact that
the zonal wind stress weakens towards the east (e.g., Fig.
5) so that remote effects take on a larger significance there.
Figure 13. Regression analysis of P
and
at (a) 117°W from November 1983 to August 1985; (b) 125°W from November 1983
to April 1986; and (c) 132°W from November 1983 to September 1985. Correlation
coefficients (r) and number of monthly data (n) are shown.
Harmonic analyses for simultaneous records centered at 117°, 125° and 132°W are summarized in Tables 2 and 3. Two separate analyses were done at 125°W for approximately year long records bracketing the wind data gap in 1984-85. Similarly, two analyses were done for the intervals centered at 117°W and 132°W, one for November 1983 to November 1984, and one for May 1984 to September 1985.
In the mean,
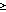P
with a maximum difference of 20%; in general, though, these two terms are not
different from one another to within one standard error (Table
2). Both the mean wind stress and the pressure gradient are significantly
stronger in the interval centered at 132°W as compared to 117°W (consistent
with Fig. 1). The nonlinear terms are smaller
than either P or
with zonal (vertical) advection being
10%-30% (35%-60%) of the pressure gradient. The sign of the nonlinear terms
is always negative implying acceleration of flow to the east, which is consistent
with the observation that the mean eastward transports along the equator are
larger than expected from linear theory. Together ½U
and WU
tend to overcompensate for the difference between wind stress and pressure gradient
by about -10 × 10 to -20 × 10
N m. This imbalance could be due to the
cumulative error involved in estimating terms in (3). However, it could also
be due to the neglect of lateral turbulent diffusion due to instability waves
which lead to an effective zonal stress of about O(-10 × 10
N m) in the upper 200-300 m of the eastern
tropical Pacific (Hansen
and Paul 1984; Bryden
et al. 1986).
Table 2 also indicates an interannual change in both the zonal wind stress and pressure gradient which nearly double between 110° and 140°W from 1983-84 to 1985-86. Thus the increase in thermocline depth and dynamic height over the record length (Figs. 8b, 10b) can be dynamically related to the increasing strength of the trades. The warmer SSTs in the latter half of the temperature record in the eastern Pacific (q.v., Fig. 8) may be related to the large scale pressure field adjustment to increased winds, since increasing the slope of the thermocline would remove the cold water reservoir further from the surface. This could reduce the efficiency of upwelling, leading to a rise in SST in spite of an expected cooling tendency due to stronger meridional Ekman divergence and zonal advection.
Table 3 presents
data on the annual harmonic in each of the three intervals centered at 117°,
125° and 132°W. We note that zonal wind stress and pressure gradient are generally
comparable in magnitude and phase if one takes into account the uncertainty
of our estimates due to sampling errors. Strongest (weakest) easterlies and
zonal pressure gradients occur from September to November (March to May) depending
on location and specific time period. However, the zonal pressure gradient in
the interval centered at 132°W does not exceed one standard error for the period
May 1984 to September 1985. At this time and location, the 60-90 day waves are
most strongly developed in pressure gradient and are of sufficient amplitude
to obscure the annual cycle. In contrast, there is an approximate balance between
P and
over the first year of data at 132°W when the waves are weaker.
The local acceleration term, U,
may be comparable at times to the zonal pressure gradient at 1 cpy, e.g., from
June 1985 to May 1986 in the interval centered at 125°W. However, estimates
of local acceleration are highly uncertain and, unlike zonal pressure gradient,
never exceed one standard error. Also, the zonal advection term does not appear
to be significant at 1 cpy. These results suggest an equilibrium balance between
zonal wind stress and pressure gradient at the annual period.
Harmonic analysis indicates that variations at 2 cpy are generally smaller than at 1 cpy and with few exceptions (notably in wind stress) statistically insignificant. Thus, while it is likely that wind-driven 2 cpy variations occur in the eastern equatorial Pacific based on previous historical data analyses and modeling studies (e.g., Meyers 1979; Kindle 1979; Busalacchi and O'Brien 1980), we cannot critically examine the dynamics at this frequency with our data. Conversely, the residuals about our six-parameter regression equation show a consistent pattern. This is illustrated for the interval centered at 132°W during May 1984-September 1985 when 60-90 day wave variability was especially pronounced (Fig. 14); similar results apply to the intervals centered at 125° and 117°W.
Figure 14. Residuals about the mean, trend, 1 and 2 cpy regression for terms
in the dynamical balance (3) at 132°W. Numbers adjacent to the time series are
root-mean-square variations in N m; maximum
cross correlation with U
is shown in parentheses. Maxima generally occur at nonzero lag, with U
leading P,
, and ½U
by 12, -3, an -1 days, respectively.
Figure 14 shows that residuals around the six-parameter
regression fit are dominated by the 60-90 day period, with the largest amplitude
fluctuations in P and U.
The maximum correlation between residuals of P
and U
is -0.66, which is significant at the 95% level of confidence. Residual U
leads P by 12 days, which
could be due to a phase shift introduced by averaging U
across longitude in (3). The zonal pressure gradient is weaker than the local
acceleration as would be expected if the residual variability were due to low
baroclinic model Kelvin waves, since the 250 m reference level is too shallow
to capture deep modal pressure variations. Indeed, referencing U
to 250 m brings the magnitude of these two terms into closer agreement. Zonal
wind stress variations are typically weaker than variations in either P
or U,
and maximum correlation between residual
and
U is only 0.42 (not significant
at the 95% level). Thus, it appears that the residual variance is remotely forced
rather than locally forced. The amplitude of the nonlinear term is only about
15% the amplitude of the local acceleration term, but significantly negatively
correlated (-0.66) with U.
Hence, nonlinearity is significant, though of secondary importance on this time
scale.
Time series measurements from surface moored buoys in the eastern and central equatorial Pacific have been analyzed for the period 1983-86. The data consist of currents, temperatures, and winds on the equator at 110°, 124.5° and 140°W. The purpose has been to examine the dynamics of upper ocean variability on seasonal and intraseasonal time scales. We have worked primarily with the depth integrated zonal momentum equation to avoid problems with poorly known vertical eddy viscosities and coarse vertical resolution of currents.
We have found that in the mean, a balance exists between depth integrated zonal pressure gradient and zonal wind stress to within 20%, in approximate agreement with linear Sverdrup theory. Conversely, we found significant mean vertical and zonal advection of momentum on the equatorial plane. This advection in part is related to the rise of the EUC towards the east in the thermocline as indicated by the tendency for the two terms to cancel one another. However, the cancellation is incomplete and the net effect of nonlinearity is to reduce the surface westward flow via upward advection of eastward momentum from the EUC. This results in larger upper-ocean eastward transports along the equator than expected from linear theory, consistent with the transport calculations shown in Fig. 6. For comparison, linear theory (e.g., McPhaden 1981; McCreary 1981) would predict nearly equal and opposite transports in the SEC and EUC, with much smaller net transport than we observed.
We found that SST was warmer by about 1°C, the thermocline was deeper by 30-40 m and dynamic height was higher by about 10 dyn cm at 140°W in 1985-86 compared to 1983-84. Likewise an interannual increase in SST was noted at 110°W beginning in 1983. These observations are consistent with those of Wyrtki (1984) and Kessler and Taft (1987) who found that the eastern and central equatorial Pacific were unusually cool in the aftermath of the 1982-83 El Niño. The interannual changes in SST we have observed between 1983 and 1986 may be related to a doubling of the zonal wind stress and a concomitant doubling of the depth integrated zonal pressure gradient. Increased easterly winds, in more strongly tilting the thermocline down towards the west, would remove the cold water reservoir to great depths and thus might reduce the efficiency of upwelling to cool the surface. This effect seems to have dominated the tendency for enhanced cooling by stronger meridional Ekman divergence and stronger advection of cool water from the east that one would expect to be associated with intensified easterlies.
Near surface zonal currents and transport appear to propagate westward along the equator at the annual period between 110° and 140°W. Although from our data we cannot determine with accuracy the magnitude of the phase speed, the inferred direction of propagation is not unexpected. Both Meyers (1979) and Lukas and Firing (1985) show from climatological ship wind data that zonal wind stress propagates westward at 1 cpy in the eastern Pacific. Also, Lukas and Firing (1985) found evidence in central Pacific temperature data for an annual, westward propagating Rossby wave which presumably has a signature in surface currents at the equator. In contrast Hayes and Halpern (1984) inferred eastward propagation of transport between 110° and 91°W (Galápagos Islands) from 16 months of current and sea level data in 1980-1981. Their data were dominated by two large eventlike features which they interpreted as first baroclinic mode Kelvin waves generated by westerly winds in the western Pacific. These events, though they happened to occur in boreal spring of each year, were probably not part of the seasonal cycle. From longer sea level and wind records, Eriksen et al. (1983) found that similar events occur at other times of the year. The greater prominence of remotely forced, eastward propagating Kelvin waves to the east of 110°W may be related to a decrease in amplitude of the annual (i.e., 12 month) period in local zonal wind stress forcing east of 110°W compared to west of 110°W.
Diagnosis of the zonal momentum equation at 1 cpy indicates that between 110°
and 140°W, local acceleration is always negligible and that the zonal pressure
gradient and wind stress tend to balance to within the errors of our analysis.
Thus, the eastern equatorial Pacific appears to be responding in a succession
of steady states to wind stress forcing at the annual period. In modeling the
annual period, Philander
and Pacanowski (1981) indicate that eastward current transport in the upper
250 m should be strongest when the zonal pressure gradient and wind stress are
most negative, i.e., in boreal fall. The exact opposite is observed in our data:
eastward current transport is largest in the spring when the pressure gradient
and easterly winds are weakest. The discrepancy may be due to lateral eddy momentum
fluxes associated with instability waves which were not evident in Philander
and Pacanowski's (1981) simulations. These instabilities lead to an effective
stress along the equator of O(-10 × 10 n
m) (Hansen
and Paul 1984; Bryden
et al. 1986). Moreover, the amplitude of the instability is largest in boreal
summer and fall and weakest in boreal spring (q.v. Fig.
3 and Philander
et al. 1985). This suggests an annual variation in lateral eddy stress which
should retard the eastward flow of the EUC more strongly in the summer and fall
than in the spring.
No consistent patterns emerged from the analysis of 2 cpy variability because of the general weakness of the signal in our records. However, at higher frequencies we found evidence for eastward propagating waves in currents, temperature, and dynamic height with periods of 60-90 days. These waves have no signature in meridional velocity and are poorly correlated with local wind forcing. Velocity, temperature, and dynamic height variations are nearly in phase and tend to be vertically coherent in the upper 250 m. Eastward phase speeds are indistinguishable from those of first baroclinic mode Kelvin waves. Analysis of the momentum balance suggests that these waves are Kelvin-like, though they may be affected by nonlinearity. Their amplitudes are large enough at times to completely obscure the annual cycle as occurred, for example, in late 1984 and early 1985.
Enfield (1987) has documented 40-60 day fluctuations in sea level propagating eastward across the equatorial Pacific and poleward along the coasts of North and South America. He interprets these as first baroclinic mode Kelvin waves excited by atmospheric 40-50 day waves (e.g., Madden and Julian 1971) which in the Pacific are most energetic west of the dateline. The period of the 60-90 day Kelvin-like waves documented in this study is longer than observed in Enfield's study. However there is reason to believe that we are observing essentially the same wave phenomenon. The data in our study overlap with Enfield's, which encompasses the period 1979-85. For this time period Enfield finds that the wind forcing and the waves are nonstationary in time and in frequency. Shortly after then 1982-83 El Niño, for example, intraseasonal fluctuations of zonal winds in the western Pacific and sea level across the Pacific weakened (q.v. his Fig. 4). Subsequently, in the latter half of 1984, zonal winds and sea level fluctuations reestablished themselves. This same pattern can be seen in currents, temperature, dynamic height, and zonal pressure gradients computed from the mooring data (e.g. Figs. 3, 8b, 10b). In addition, sea level spectra presented in Enfield (his Fig. 6) suggest that after the 1982-83 El Niño, the period of the waves increased to about 70 days. To verify this, we calculated the periodogram and energy spectrum of Christmas Island sea level data from 1983-85 and found a large peak between 60 and 90 days with maximum periodogram estimate at a period of 73 days. Thus we conclude that the 60-90 day waves observed in the mooring data are essentially the same phenomenon that Enfield documented in sea level, but shifted to lower frequency during the time period of our analysis.
Acknowledgments. The authors would like to thank P. Freitag and M. McCarty for processing the mooring and XBT data used in this analysis. We are also indebted to A. Shepherd for his careful preparation and calibration of the VACMs and wind recorders for each deployment; and to D. Fenton of SeaMarTec, Inc., who oversaw mooring assembly, deployment, and recovery procedures. We would also like to thank W. Kessler, E. Johnson, D. Enfield, and S. Hayes for comments on an earlier version of this manuscript. K. Wyrtki kindly provided the sea level data from Christmas Island. This research was conducted as part of NOAA's Equatorial Pacific Ocean Climate Studies (EPOCS) Program.
Bendat, J.S., and A.G. Pierson, 1971: Random Data: Analysis and Measurement Procedures. Wiley-Interscience, 407 pp.
Bryden, H.L., 1977: Geostrophic comparisons of moored measurements of current and temperature during the Mid-Ocean Dynamics Experiment. Deep-Sea Res., 24, 677-681.
Bryden, H.L., and E.C. Brady, 1985: Diagnostic model of the three-dimensional circulation in the upper equatorial Pacific Ocean. J. Phys. Oceanogr., 15, 1255-1273.
Bryden, H.L., E.C. Brady, and D. Halpern, 1986: Lateral mixing in the equatorial Pacific Ocean. Further Progress in Equatorial Oceanography. E. Katz and J. Witte, Eds., Nova University Press, 121-132.
Busalacchi, A.J., and J.J. O'Brien, 1980: The seasonal variability in a model of the tropical Pacific. J. Phys. Oceanogr., 10, 1929-1950.
Cane, M.E., 1979: The response of an equatorial ocean to simple wind stress patterns, II: Numerical results. J. Mar. Res., 37, 233-252.
Cane, M.E., 1980: On the dynamics of equatorial currents, with application to the Indian Ocean. Deep-Sea Res., 27A, 525-544.
Cane, M.E., and E.S. Sarachik, 1981: The response of a linear baroclinic equatorial ocean to periodic forcing. J. Mar. Res., 39, 651-693.
Davis, R.E., 1976: Predictability of sea surface temperature and sea level pressure anomalies over the North Pacific Ocean. J. Phys. Oceanogr., 6, 249-266.
Draper, N.R., and H. Smith, 1966: Applied Regression Analysis. J. Wiley and Sons, 407 pp.
Enfield, D., 1987: The intraseasonal oscillation in eastern Pacific sea levels: How is it forced? J. Phys. Oceanogr., 17, 1860-1876.
Eriksen, C.E., 1985: The Tropic Heat Program: An overview. Eos, Trans. Amer. Geophys. Union, 66, 50-54.
Eriksen, C.E., M.B. Blumenthal, S.P. Hayes, and P. Ripa, 1983: Wind generated equatorial Kelvin waves observed across the Pacific Ocean. J. Phys. Oceanogr., 13, 1622-1640.
Fofonoff, N.P., and R.B. Montgomery, 1955: The equatorial undercurrent in the light of the vorticity balance. Tellus, 7, 518-521.
Freitag, H.P., M.J. McPhaden, and A.J. Shepherd, 1987: Equatorial current and temperature data: 108°W to 110°W: October 1979 to November 1983. NOAA Data Rep. ERL PMEL-17, 99 pp.
Gent, P.R., K. O'Neill, and M.A. Cane, 1983: A model of the semiannual oscillation in the equatorial Indian Ocean. J. Phys. Oceanogr., 13, 2148-2160.
Goldenberg, S.P., and J.J. O'Brien, 1981: Time and space variability of tropical Pacific wind stress. Mon. Wea. Rev., 109, 1190-1207.
Halpern, D., 1980: A Pacific equatorial temperature section from 172°E to 110°W during winter and spring 1979. Deep-Sea Res., 27, 931-940.
Halpern, D., 1987a: Observations of annual El Niño thermal and flow variations at 0°, 110°W and 0°, 95°W during 1980-85. J. Geophys. Res., 92, 8197-8212.
Halpern, D., 1987b: Comparison of upper ocean VACM and VMCM observations in the equatorial Pacific. J. Atmos. Oceanic Technol., 4, 84-93.
Halpern, D., 1987c: Comparison of moored wind measurements from a spar and toroidal buoy in the eastern equatorial Pacific during February-March 1981. J. Geophys. Res., 92, 8303-8306.
Halpern, D., 1987d: On the monthly sampling of mean wind speeds over the equatorial Pacific. Eos, Trans. Amer. Geophys. Union, 68, 1321-1322.
Halpern, D., and P. Freitag, 1987: Vertical motion in the upper ocean of the equatorial eastern Pacific. Oceanologica Acta, Proc. Int. Symp. on Equatorial Vertical Motion, 19-26 pp.
Hansen, D.V., and C.A. Paul, 1984: Genesis and effects of long waves in the equatorial Pacific. J. Geophys. Res., 89, 10,431-10,440.
Hayes, S.P., 1981: Vertical finestructure observations in the eastern equatorial Pacific. J. Geophys. Res., 86, 10,983-10,999.
Hayes, S.P., and D. Halpern, 1984: Correlation of current and sea level in the eastern equatorial Pacific. J. Phys. Oceanogr., 14, 811-824.
Hayes, S.P., D.W. Behringer, M. Blackmon, D.V. Hansen, N.-C. Lau, A. Leetmaa, S.G.H. Philander, E.J. Pitcher, C.S. Ramage, E.M. Rasmussen, and others, 1986: The Equatorial Pacific Ocean Climate Studies (EPOCS) plans: 1986-1988. Eos, Trans. Amer. Geophys. Union, 67, 442-444.
Horel, J.D., 1982: On the annual cycle of the tropical Pacific atmosphere and ocean. Mon. Wea. Rev., 110, 1863-1878.
Jenkins, G.M., and D.G. Watts, 1968: Spectral Analysis and Its Applications. Holden-Day, 525 pp.
Katz, E.J., R. Belevich, J. Bruce, J. Cochrane, W. Duing, P. Hisard, H.U. Lass, J. Meinke, A. de Mesquita, L. Miller, and A. Rybnikov, 1977: Zonal pressure gradient along the equatorial Atlantic. J. Mar. Res., 35, 293-307.
Katz, E.J., P. Hisard, J.-M. Verstraete, and S.L. Garzoli, 1986: Annual change of sea surface slope along the equator of the Atlantic Ocean in 1983 and 1984. Nature, 322, 245-247.
Kessler, W.S., and B.A. Taft, 1987: Dynamic heights and zonal transports in the central tropical Pacific during 1979-1984. J. Phys. Oceanogr., 17, 97-112.
Kessler, W.S., B.A. Taft, and M.J. McPhaden, 1985: An assessment of the XBT sampling network in the central Pacific. University Corporation for Atmospheric Research, Tech. Rep. USTOGA No. 4, 62 pp.
Kindle, J.C., 1979: Equatorial Pacific Ocean variability--seasonal and El Niño time scales. Ph.D. dissertation, Florida State University, 134 pp.
Knauss, J.A., 1966: Further measurements and observations of the Cromwell Current. J. Mar. Res., 24, 205-240.
Knox, R.A., and D. Halpern, 1982: Long range Kelvin wave propagation of transport variations in Pacific Ocean equatorial currents. J. Mar. Res., 40 (Suppl.), 329-339.
Large, W.G., and S. Pond, 1982: Sensible and latent heat flux measurements over the ocean. J. Phys. Oceanogr., 12, 464-482.
Legeckis, R., W. Pichel, and G. Nesterczuk, 1983: Equatorial long waves in geostationary satellite observations and in multichannel sea surface temperature analysis. Bull. Amer. Meteor. Soc., 64, 113-139.
Lukas, R., and E. Firing, 1984: The geostrophic balance of the Pacific Equatorial Undercurrent. Deep-Sea Res., 31, 61-66.
Lukas, R., and E. Firing, 1985: The annual Rossby wave in the central equatorial Pacific. J. Phys. Oceanogr., 15, 55-67.
Luther, D.S., and D.E. Harrison, 1984: Observing long-period fluctuations of surface winds in the tropical Pacific: Initial results from island data. Mon. Wea. Rev., 112, 285-302.
McCreary, J.P., Jr., 1981: A linear, stratified model of the Equatorial Undercurrent. Phil. Trans. Roy. Soc. London, A298, 603-635.
McPhaden, M.J., 1981: Continuously stratified models of the steady state equatorial ocean. J. Phys. Oceanogr., 11, 337-354.
McPhaden, M.J., 1982: Variability in the central equatorial Indian Ocean, Part I: Ocean dynamics. J. Mar. Res., 40, 157-176.
McPhaden, M.J., H.P. Freitag, S.P. Hayes, B.A. Taft, Z. Chen, and K. Wyrtki, 1988: The response of the equatorial Pacific to a westerly wind burst in May 1986. J. Geophys. Res., 93, 10,589-10,603.
Madden, R.A., and P.R. Julian, 1971: Detection of a 40-50 day oscillation in the zonal wind in the tropical Pacific. J. Atmos. Sci., 28, 702-708.
Mangum, L.J., and S.P. Hayes, 1984: The vertical structure of the zonal pressure gradient in the eastern equatorial Pacific. J. Geophys. Res., 89, 10,441-10,449.
Meyers, G., 1979: Annual variation in the slope of the 14°C isotherm along the equator in the Pacific Ocean. J. Phys. Oceanogr., 9, 885-891.
Pedlosky, J., 1987: An inertial theory of the Equatorial Undercurrent. J. Phys. Oceanogr., 17, 1978-1985.
Peters, H., M.C. Gregg, and J.M. Toole, 1988: On the parameterization of equatorial turbulence. J. Geophys. Res., 93, 1119-1218.
Philander, S.G.H., 1979: Variability of the tropical oceans. Dyn. Atmos. Oceans, 3, 191-208.
Philander, S.G.H., and R.C. Pacanowski, 1980: The generation of equatorial currents. J. Geophys. Res., 85, 1123-1136.
Philander, S.G.H., and R.C. Pacanowski, 1981: Response of equatorial oceans to periodic forcing. J. Geophys. Res., 86, 1903-1916.
Philander, S.G.H., D. Halpern, D. Hansen, R. Legeckis, L. Miller, C. Paul, R. Watts, R. Weisberg, and M. Wimbush, 1985: Long waves in the equatorial Pacific Ocean. Eos, Trans. Amer. Geophys. Union, 66, 154-155.
Puls, C., 1895: Oberfl„chentemperaturen und Str”mungsverh„ltmisse des Aquatorialgrtels des Stillen Ozeans. Dtsch. Arch. Seewarte, 18, 1-38.
Rothstein, L.M., 1984: A model of the equatorial sea surface temperature field and associated circulation dynamics. J. Phys. Oceanogr., 14, 1875-1892.
Sverdrup, S.U., 1947: Wind-driven currents in a baroclinic ocean with application to the equatorial currents of the eastern Pacific. Proc. Natl. Acad. Sci., 33, 318-326.
Tsuchiya, M., 1979: Seasonal variations of the equatorial zonal geopotential gradient in the eastern Pacific Ocean. J. Mar. Res., 37, 399-407.
Weisberg, R.H., D. Halpern, T.Y. Tang, and S.M. Hwang, 1987: M
tidal currents in the eastern equatorial Pacific
Ocean. J. Geophys. Res., 92, 3821-3826.
Wyrtki, K., 1984: The slope of sea level along the equator during the 1982/1983 El Niño. J. Geophys. Res., 89, 10,419-10,424.
Wyrtki, K., and G. Meyers, 1975: The trade wind field over the Pacific Ocean, I: The mean field and the mean annual variation. Tech. Rep. HIG-75-1, Hawaii Institute of Geophysics, University of Hawaii, 26 pp. Figures and Tables.
Return to Abstract