U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
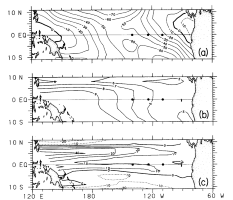
Figure 1. (a) Mean zonal wind stress (in 10
N m
) from 1961-83 from ship wind analyses
(Goldenberg
and O'Brien 1981) using a drag coefficient of 1.2 × 10
and air density of 1.2 kg m; (b) depth integrated
pressure (in 10
N m
)
from the Sverdrup
(1947) balance. Values are relative to an arbitrary integration constant
chosen as 5 × 10 N m;
(c) Zonal transport per unit width (in m
s)
from the Sverdrup relation. Dashed lines in (c) indicate negative values. Positions
of the current meter moorings are shown by the solid dots at 110°, 124.5° and
140°W.
Figure 2. Zonal section of temperature and dynamic height (0/250 m dashed and 0/450 m solid) from XBT casts in October 1985 showing mooring positions and VACM depths.
Figure 3. Daily averages of (a) zonal velocity (b) meridional velocity, and (c) temperature at 0°N, 140°W at depths of 25 m, 80 m and 160 m. Smooth curves are for daily data smoothed with a 51-day Hanning filter.
Figure 4. Variance preserving spectra for zonal velocity and temperature shown in Fig. 3 at 0°N, 140°W for daily data. Spectral estimates are based on averages over five adjacent frequency bands. Note that the ordinates are scaled differently at each depth.
Figure 5. Zonal wind stress data at the mooring sites smoothed with a 51-day Hanning filter. Dashed lines are data interpolated according to a procedure outlined in section 5.
Figure 6. Equatorial current and transport time series smoothed with a 51-day
Hanning filter at (a) 110°W and (b) 140°W. Dashed contours indicate westward flow; cross
hatching indicates eastward flow >100 cm s. Means
calculated from a six-parameter regression analysis (see section 3) are shown on the
right. Total (eastward) transport per unit width in the upper 250 m is indicated by the
solid (dashed) line.
Figure 7. Cross-correlation analyses for zonal currents at 25 and 160 m depth between 110°-124.5°W, 110°-140°W and 124.5°-140°W. Data have been demeaned and detrended. Maximum correlation (r) and corresponding lag in days is shown in upper left of each panel. Positive (negative) lag means that the second time series lags (leads) the first. Heavy tick marks indicate 90% confidence limits for the null hypothesis calculated using the integral time scale to estimate degrees of freedom (Davis 1976). Integral time scale is based on correlation calculations for lags up to ±2 years and is about 5-6 months at 25 m and 1-2 months at 160 m; only lags to ±180 days are plotted for brevity.
Figure 8. Time series of isotherm depths and SST smoothed with a 51-day Hanning filter at (a) 110°W and (b) 140°W. Means calculated from a six-parameter regression analysis (see section 3) are shown on the right.
Figure 9. Cross-correlation analyses of currents and temperature at 110°, 124.5° and 140°W from a depth of 160 m. Positive (negative) lags imply that temperature leads (lags) zonal velocity. Format is otherwise as in Fig. 7.
Figure 10. Dynamic height variations relative to 250 m smoothed with a 51-day Hanning filter at (a) 110°W and (b) 140°W. Means calculated from a six-parameter regression analysis are shown on the right.
Figure 11. Time series estimates of (a) zonal pressure gradient, p
, relative to 250 m, (b) local acceleration, 
u
, and (c)
zonal advection, ½u for the
interval centered at 125°W. Contour interval is 1.0 × 10
N m, though the ±0.5
× 10 N m contour
is also drawn. Means are estimated from a 6-parameter regression fit. Dashed line in the
mean panel of (c) is the vertical advection term WU
.
Figure 12. Estimates (in N m) of terms in (3)
for the intervals centered at (a) 117°, (b) 125° and (c) 132°W. Shown in the uppermost
panel at each location is ten times the vertical shear stress at 250 m. Also shown as
dotted and long dashed lines are time series reconstituted from the least squares
determined trend, mean, and 1 cpy variations.
Figure 13. Regression analysis of P and 
at (a) 117°W from November 1983 to
August 1985; (b) 125°W from November 1983 to April 1986; and (c) 132°W from November
1983 to September 1985. Correlation coefficients (r) and number of monthly data (n)
are shown.
Figure 14. Residuals about the mean, trend, 1 and 2 cpy regression for terms in the
dynamical balance (3) at 132°W. Numbers adjacent to the time series are root-mean-square
variations in N m; maximum cross correlation with U is shown
in parentheses. Maxima generally occur at nonzero lag, with U
leading P, , and ½U by 12, -3, an
-1 days, respectively.
Table 1. Locations, dates, durations and depths of moorings along the equator.
Table 2. Means (in 10 N m) in terms in (3) derived by a least squares regression
analysis of overlapping time series for intervals centered at 117°, 125° and 132°W. The
(X) indicates that no calculation was performed because the record was shorter than one
year. One standard error is indicated for each estimate except for WU which
is based on a mean W from Bryden and Brady (1985) rather than time series data (see
text for discussion). Estimates that do not exceed one standard error are shown in
parentheses.
Table 3. Amplitudes (in 10 N m) and phases (in days since January 1) of the annual (i.e.,
1 cpy) harmonic derived from least squares regression analysis for the intervals centered
at 117°, 125° and 132°W. The (X) indicates that no calculation was performed because
the record was shorter than one year. One standard error is indicated for each estimate;
amplitude estimates that do not exceed one standard error are shown in parentheses, as are
accompanying phase estimates.
Go back to References
Return to Abstract
