U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
Buoyancy-driven plumes in rotating, stratified cross flows: Plume dependence on
rotation, turbulent mixing, and cross-flow strength
J. W. Lavelle
National Oceanic and Atmospheric Administration/Pacific Marine Environmental
Laboratory, Seattle, Washington
Journal of Geophysical Research, 102(C2), 3405-3420 (1997)
Not subject to U.S. copyright. Published in 1997 by the American Geophysical Union.
Abstract
A three-dimensional time-dependent convection model is used to describe circulation
and property fields in rotating, stratified, and moving fluids near a point
source of heat. The study context and, consequently, model scales are those
of chronically discharging hydrothermal vent fields found at submarine ridge
crests. Hydrothermal plumes having distinctive thermal and chemical anomalies
have been observed to rise several hundreds of meters above the deep-sea floor
before being advected away by background cross flows typically of magnitude
1-4 cm s . The model is used to study effects
of rotation and indicate differences in plumes with respect to variation of
subgrid-scale turbulence intensity and cross-flow strength. Counterrotating
vorticity (
. The model is used to study effects
of rotation and indicate differences in plumes with respect to variation of
subgrid-scale turbulence intensity and cross-flow strength. Counterrotating
vorticity ( ) couplets in all three coordinate
directions develop in the lower plume stem at startup and follow the plume to
the level of neutral buoyancy; for a nonrotational case (
) couplets in all three coordinate
directions develop in the lower plume stem at startup and follow the plume to
the level of neutral buoyancy; for a nonrotational case ( = 0),
= 0),  patterns resemble those previously found
for jets injected into homogenous cross flow. Ambient fluid entrainment into
the convecting column is primarily from the upstream side, but deflection of
background flow around both sides of the rising column is the root of the relative
vorticity (
patterns resemble those previously found
for jets injected into homogenous cross flow. Ambient fluid entrainment into
the convecting column is primarily from the upstream side, but deflection of
background flow around both sides of the rising column is the root of the relative
vorticity ( z) couplet in the
lower plume. Turbulence intensity within the buoyant region of the plume and/or
globally controls smoothness and temporal variability of distal nonbuoyant plume
distributions, allowing or preventing oscillations of potential temperature,
z) couplet in the
lower plume. Turbulence intensity within the buoyant region of the plume and/or
globally controls smoothness and temporal variability of distal nonbuoyant plume
distributions, allowing or preventing oscillations of potential temperature,
 , for example, at background buoyancy frequency,
N. Over the range of turbulent mixing studied, rise height of plumes
did not change appreciably, but breadth of plumes, counterintuitively, increased
for decreasing turbulent mixing strength. Increasing cross-flow strength, U
, for example, at background buoyancy frequency,
N. Over the range of turbulent mixing studied, rise height of plumes
did not change appreciably, but breadth of plumes, counterintuitively, increased
for decreasing turbulent mixing strength. Increasing cross-flow strength, U ,
bends model plumes such that rise height
,
bends model plumes such that rise height 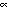 U
U -0.4.
For the two largest values of cross flow, for which R, the ratio of maximum
vertical velocity to U
-0.4.
For the two largest values of cross flow, for which R, the ratio of maximum
vertical velocity to U , took
values of 2.8 and 1.0, plumes showed evidence of bifurcation.
, took
values of 2.8 and 1.0, plumes showed evidence of bifurcation.
Introduction
Convection from near-point sources of buoyancy occurs at the deep-sea floor
where hot hydrothermal fluids are steadily vented. All along ridge crest spreading
centers, buoyant plumes rich in chemicals and particles ascend several hundred
meters into the water column while being bent over and advected away by ambient
currents [Baker
et al., 1995]. In those benthic environments, cross-flow strength,
fluid turbulence, planetary rotation, background stratification, and source
buoyancy flux all combine to determine dispersion patterns of heat and other
constituents emanating from hydrothermal vents. In this paper, a model of buoyant
plumes in rotating, stratified cross flows appropriate to conditions of ridge
crest hydrothermal plumes is described. The focus of results is on rotation,
intensity of turbulent mixing, and cross-flow strength as factors that determine
downstream plume attributes.
Hydrothermal plumes are one of many examples in the natural environment where
a localized source of buoyancy causes materials to rise into an overlying fluid
and forced circulation to develop. In all cases, turbulence and, in many cases,
rotation and cross flow are important to the dynamics of ensuing plumes. Plumes
from industrial stacks, terrestrial volcanoes, forest fires, and oceanic thermal
and waste water discharges provide instances of buoyant plumes or buoyant jets
occurring in a cross flow. A related problem in the industrial realm involves
injection of one fluid as a jet into another as occurs, for example, with fuel
injection into jet engines [e.g.,
Claus and Vanka, 1992]. Numerical model results for jets entering
unstratified, nonrotating cross flows [Sykes
et al., 1986] provide useful points of comparison for results
here. Jets and buoyant jets are different from buoyant plumes in that jets have
momentum at source points independent of forces of buoyancy caused by density
anomalies. Buoyant plumes, which lack initial upward momentum, are reasonable
idealizations for many hydrothermal discharges; initial upward momentum found
at a typical hydrothermal vent orifice must give way to buoyancy forces within
vertical distances very much smaller than plume rise height.
Model approaches to plumes of this kind are generally classified as integral
or numerical. The seminal paper for the integral method is that of Morton
et al. [1956], who closed one-dimensional vertical mass, momentum,
and heat conservation equations by making fluid entrainment into the rising
plume stem at each level proportional to plume upward velocity. The resulting
set of ordinary differential equations can be readily solved to address maximum
rise height and dilutions within the plume stem. On the other hand, integral
models provide no information on distributions in the plume cap region or in
regions exterior to the plume where recirculations develop. The integral approach
has since been extended and heavily used to describe a variety of jets and plumes,
including those rising into cross flows [e.g.,
Slawson and Csanady, 1967; Middleton
and Thomson, 1986; Davidson,
1989]. The literature on jets, buoyant jets, and plumes in cross
flows is extensive; reviews by List
[1982], Hanna
et al. [1982], and Weil
[1988] are good sources of information on fundamentals of integral
models.
Unlike integral models, more computationally taxing numerical models allow
plume cap distributions and induced circulation surrounding the plume to be
computed. No uniform entrainment coefficient need be assumed, though as in all
fluid dynamical models a turbulent mixing closure assumption of some kind is
required. Numerical models of plumes have tended to be two-dimensional [e.g.,
Lilly, 1962] or quasi-three-dimensional (3-D) [Golay,
1982; Zhang
and Ghoniem, 1994] because of computational demands. On the other
hand, models of thunderstorms [e.g.,
Klemp, 1987] and cumulus cloud formation [e.g.,
Smolarkiewicz and Clark, 1985] have shown the benefits of
full 3-D approaches for some time, and those convection problems bear some commonality
with point source plume problems. In some sense the oceanic convection problem
is easier: source point is stationary, initial conditions are more easily prescribed,
and fluid can be assumed to be incompressible.
Hydrothermal plumes result from episodic and chronic discharges of chemically
anomalous, heated water at the seafloor along crustal spreading centers. Plumes
are of two main types. Megaplumes appear to be the result of short-lived discharge
events [Lavelle,
1995]. These plumes are kilometers in diameter and hundreds of meters
in thickness and rise many hundreds to a thousand or more meters above the seafloor
[e.g.,
Baker et al., 1995]. The plumes are characterized by thermal
anomalies as large as ~0.3°C [e.g.,
Baker et al., 1995] and by their distinctive chemical signatures
[e.g.,
Massoth et al., 1995]. The few observed have been associated
with linear crustal ruptures brought on by episodic magmatic intrusions that
rise from depth to the seafloor leaving telltale lava flows [Embley
et al., 1995; Fox
et al., 1995]. More commonly observed are hydrothermal plumes
that result from the continuous release of heat and chemicals stripped from
the underlying rock by the hot fluids. Fluxes from chronic sources individually
are many orders of magnitude less than those that result in megaplumes, but
in aggregate over a ridge crest segment and over a year's time, flux is comparable.
Chronic discharge can emanate from sulfide chimneys, e.g., black and white smoker
chimneys, more diffusely from sulfide mounds typically meters on a side [e.g.,
Delaney et al., 1992], or it can percolate from seafloor fissures.
Heat release from single vents is estimated to range from several to tens of
megawatts [e.g.,
Schultz et al., 1992] and from vent fields from several hundreds
to several thousand megawatts [Baker
et al., 1996]. Because heat release is continuous in these cases,
background current flows play a major role in plume development.
Observations of effects on the thermal, chemical, and particulate environments
resulting from chronic discharges at ridge crests are numerous and are summarized
by Baker
et al. [1995]. Plumes from chronic sources rise several hundred
meters into the water column before reaching density equilibrium. Measured temperature
anomalies in the nonbuoyant plume region are typically <0.05 °C [Baker
et al., 1995]. Such plumes are also made distinctive by their
particle [e.g.,
Feely et al., 1992], metal [e.g.,
Massoth et al., 1994], and gas content [e.g.,
Lupton and Craig, 1977; Mottl
et al., 1995]. Transects made along the strike of ridge crests
show that plumes from chronic sources can extend longitudinally for many tens
of kilometers, as plumes from separate sources coalesce in background currents,
which are often along ridge [Cannon
et al., 1991]. The model in this paper is intended to address
features of a plume from a single, somewhat broad chronic discharge site, e.g.,
a sulfide mound.
Until now, there have been no models for chronic discharge of hydrothermal
fluids that could address the three-dimensional distributions of plume properties
in the nonbuoyant region and connect them with source discharge. The challenge
of dealing with open boundary conditions when background flows are superimposed
on the convection has been one reason for this absence. But the need for a plume
model incorporating background flow is clear. Observations typically show that
background currents advect hydrothermal plumes away from their source points.
Furthermore, without lateral advection, thermal equilibrium cannot be achieved
in any fixed volume enclosing a chronically discharging hydrothermal vent.
The plan of the paper is to set out the design of the numerical model, show
results for a reference case, and then look at variations in results for changes
in single model parameters. The reference case is calculated for source buoyancy
flux, cross flow, and background stratification like those expected for hydrothermal
discharges on the Juan de Fuca Ridge (JDFR) in the northeast Pacific. The reference
case is then compared with a nonrotational case, with results of two experiments
in which turbulent mixing is reduced, and with results of two experiments where
cross flow is doubled and quadrupled. The emphasis of this initial report is
on the general character of model plumes rather than on specific details of
their dynamics.
Model Formulation
Governing Equations
The model describes a thermal plume rising into a temperature- and salinity-stratified
background environment marked by steady, vertically sheared cross flow. The
fluid is incompressible and the response to the localized buoyancy source nonhydrostatic.
Together with the equation of state for seawater [Fofonoff
and Millard, 1983], the underlying model equations in the Boussinesq
approximation are
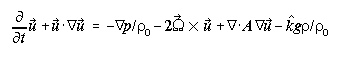 |
(1) |
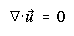 |
(2) |
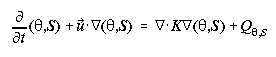 |
(3) |
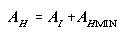 |
(4) |
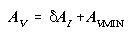 |
(5) |
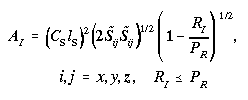 |
(6) |
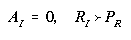 |
(7) |
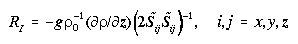 |
(8) |
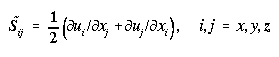 |
(9) |
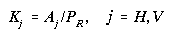 |
(10) |
where t is time; 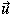 consists of u, v, and vertical w (positive upward) components;
p is pressure;
consists of u, v, and vertical w (positive upward) components;
p is pressure;  is density;
is density; 
 (1028.11 kg m
(1028.11 kg m ) is a reference density; g
(9.81 m
) is a reference density; g
(9.81 m s
s )
is acceleration of gravity;
)
is acceleration of gravity;  is the rotation
vector; and
is the rotation
vector; and 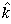 is the unit vector in the vertical direction. Potential temperature,
is the unit vector in the vertical direction. Potential temperature,  ,
and salinity, S, depend on rates of discharge of heat QH,
via Q
,
and salinity, S, depend on rates of discharge of heat QH,
via Q = QH
/(
= QH
/(
 CP),
and salt QS, where CP (4200 J kg
CP),
and salt QS, where CP (4200 J kg °C
°C ) is the specific heat of seawater. Equations
(1)-(3) are statements of conservation for momentum, mass (given fluid incompressibility),
and heat (or salt). Chemical tracers have conservation equations analogous to
(3). Retention of all terms in the vertical force balance in (1) makes the model
nonhydrostatic. The viscosity tensor A and diffusivity tensor K
are time- and space-dependent; diffusive transport is down gradient.
) is the specific heat of seawater. Equations
(1)-(3) are statements of conservation for momentum, mass (given fluid incompressibility),
and heat (or salt). Chemical tracers have conservation equations analogous to
(3). Retention of all terms in the vertical force balance in (1) makes the model
nonhydrostatic. The viscosity tensor A and diffusivity tensor K
are time- and space-dependent; diffusive transport is down gradient.
Equations (4)-(10) constitute the turbulent mixing submodel. Horizontal and
vertical components of mixing tensors AH or V (and
KH or V via (10)) are each composed of two parts: an
isotropic (AI) mixing coefficient and either horizontal (AHMIN)
or vertical (AVMIN) background terms (equations (4)-(5)).
The isotropic mixing coefficient AI (equation (6)) is made
to depend on fluid shear (Sij, here given in Cartesian form,
(9)), on shear Richardson number (RI (8)), on Prandtl number
(PR (10)), and on the turbulence length scale (lS)
and Smagorinsky (CS) constants (equation (6)). If RI
were zero, (6) would reduce to a form originating with Smagorinsky
[1963]; it stems from an assumed local balance between shear production
and turbulence dissipation in the turbulence kinetic energy (TKE) equation.
When buoyancy production or dissipation is added to the local TKE balance, the
RI dependent factor becomes part of the formulation [Lilly,
1962]. Advection and diffusion of TKE are generally found to represent
small contributions to the TKE equation balance when explicitly evaluated, and
they are here implicitly set to zero. Mixing terms have no explicit dependence
on rotation. The reason is that in forming TKE, terms involving  sum to zero.
sum to zero.
Smagorinsky-Lilly mixing, with or without the RI dependent
factor, is in widespread use in atmospheric calculations [e.g.,
Clark and Farley, 1984; Mason,
1989]. Subgrid-scale mixing of this type is frequently used in
large eddy simulations (LES) of both engineering and geophysical natures [e.g.,
Reynolds, 1990; Galperin
and Orszag; 1993; Smagorinsky,
1993; Mason,
1994]. Following the nomenclature of Reynolds
[1990], Wyngaard
[1990] notes that models using this kind of turbulence closure should
actually be typed very large eddy simulation (VLES). VLES implies that, although
resolved scales include much of the eddy energy, model resolution is not high
enough that smallest resolved scales fall within the subinertial range of turbulence
where details of dissipation ought not to matter.
Background mixing terms (equations (4)-(5)), presumed to be small, have here
been added to AI to ensure a modest amount of mixing in regions
without shear, e.g., away from the plume region, where AI
will be zero. Other closure models are in current use as well. Sykes
et al. [1986] used a full TKE equation to determine q,
the square root of twice TKE; turbulent mixing was then made proportional to
the product of q and lS. In both the present, Sykes
et al.'s, and many other approaches, lS has a size that is
imposed rather than calculated. The model summarized by (1)-(10), but without
cross flow, has been studied in the context of laboratory convection experiments
as a way of investigating the value of the subgrid turbulence closure subcomponent
[Lavelle
and Smith, 1996].
For hydrothermal venting, convective flow is forced by a source of heat at
interior points along the lower boundary of the region of interest. Steady background
cross flow is forced by a constant horizontal pressure gradient, 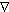 P
P .
Without point source heating, the steady background velocity profile uBKG
= (uBKG, vBKG) results from an Ekman horizontal
force balance (equation (1)):
.
Without point source heating, the steady background velocity profile uBKG
= (uBKG, vBKG) results from an Ekman horizontal
force balance (equation (1)):
- 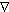 P P / /  - 2
- 2  × uBKG + d/dz
[Az d(uBKG)/dz] =
0 × uBKG + d/dz
[Az d(uBKG)/dz] =
0 |
(11) |
and boundary conditions uBKG = 0 (z = 0, bottom) and
duBKG/dz = 0 (z = h, top). With
uniform 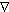 P
P in the y direction, nonzero
in the y direction, nonzero  , and Az
profiles that increase toward the seafloor as described later, flow is oriented
in the x direction except near the bed. Profiles uBKG
and vBKG (e.g., Figure 1a)
were used to initialize velocity fields and maintain upstream velocity boundary
conditions thereafter. Without source heat (and/or salt), uBKG and
vBKG are maintained numerically over time as solutions to
(1)-(10) as they must be. In reference experiment 21 (Table 1), outside the
boundary layer, uBKG was 1.5 cm s
, and Az
profiles that increase toward the seafloor as described later, flow is oriented
in the x direction except near the bed. Profiles uBKG
and vBKG (e.g., Figure 1a)
were used to initialize velocity fields and maintain upstream velocity boundary
conditions thereafter. Without source heat (and/or salt), uBKG and
vBKG are maintained numerically over time as solutions to
(1)-(10) as they must be. In reference experiment 21 (Table 1), outside the
boundary layer, uBKG was 1.5 cm s ,
while vBKG was nonzero only within that layer (Figure
1a). Mean currents of that magnitude are typical at ridge crest depths on
the JDFR [e.g.,
Cannon et al., 1991].
,
while vBKG was nonzero only within that layer (Figure
1a). Mean currents of that magnitude are typical at ridge crest depths on
the JDFR [e.g.,
Cannon et al., 1991].
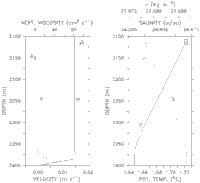
Figure 1. Idealized environmental profiles for u, v,
AZ,  , S, and
, S, and 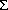 .
Profile shapes and magnitudes nominally represent conditions in the lowest 300
m of water column above the seafloor spreading center of the Juan de Fuca Ridge,
northeast Pacific. The AZ profile controlling the boundary
layer thickness is hypothetical, but the shape and magnitude are generally consistent
with AZ values deduced from benthic ocean measurements at
other sites.
.
Profile shapes and magnitudes nominally represent conditions in the lowest 300
m of water column above the seafloor spreading center of the Juan de Fuca Ridge,
northeast Pacific. The AZ profile controlling the boundary
layer thickness is hypothetical, but the shape and magnitude are generally consistent
with AZ values deduced from benthic ocean measurements at
other sites.
If your browser cannot view the following table correctly,
click this link for a GIF image of Table
1
Table 1. Parameter Values for the Convective Plume Experiments
|
| Exp. No. |
2 Z, Z,
s |
CS |
AH
MIN,
cm s s |
U , ,
m s |
h,
m |
|
| 21 |
1.03 × 10 |
0.2 |
100 |
0.015 |
300 |
| 22 |
0 |
0.2 |
100 |
0.015 |
300 |
| 23 |
1.03 × 10 |
0 |
100 |
0.015 |
300 |
| 26 |
1.03 × 10 |
0.2 |
10 |
0.015 |
300 |
| 24 |
1.03 × 10 |
0.2 |
100 |
0.03 |
200 |
| 25 |
1.03 × 10 |
0.2 |
100 |
0.06 |
150 |
|
The vertical force balance without heating is hydrostatic: dP /dz
= g
/dz
= g BKG, where
BKG, where  BKG
is background density; wBKG = 0. The variable p in (1)
thus represents the sum of P
BKG
is background density; wBKG = 0. The variable p in (1)
thus represents the sum of P (z),
P
(z),
P (x,y), and
a perturbation pressure p
(x,y), and
a perturbation pressure p (x,y,z)
caused by heating. In actual practice, hydrostatic terms are first subtracted
from (1), with the consequence that in resulting equations, p represents
the sum of P
(x,y,z)
caused by heating. In actual practice, hydrostatic terms are first subtracted
from (1), with the consequence that in resulting equations, p represents
the sum of P and p
and p and
and  becomes
becomes 
 = (
= ( -
-  BKG
).
BKG
).
Background profiles (Figures 1a-1b) hinge on
the form given Az. To simplify the initialization process
and make background profiles independent of boundary layer shear,  of (4) was set to zero. Vertical turbulent mixing coefficients are thus fixed
from the start of calculations. Because vertical mixing rates in the ocean are
small in the interior (AZMIN) and increase (to AZMAX)
as z
of (4) was set to zero. Vertical turbulent mixing coefficients are thus fixed
from the start of calculations. Because vertical mixing rates in the ocean are
small in the interior (AZMIN) and increase (to AZMAX)
as z  0 [e.g.,
Garrett, 1979], the profile for A
0 [e.g.,
Garrett, 1979], the profile for A (Figure 1a) was given the form
(Figure 1a) was given the form
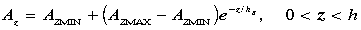 |
(12) |
where hB determines the boundary layer thickness. The value
of Az declines to within 1% of AZMIN by
a distance of 5 hB of the seafloor (z = 0). Values
of AZMIN = 1 cm s
s ,
AZMAX = 100 cm
,
AZMAX = 100 cm s
s ,
and a viscosity height scale length hB = 10 m were taken as
nominally representative of benthic ocean conditions.
,
and a viscosity height scale length hB = 10 m were taken as
nominally representative of benthic ocean conditions.
Without heating, background profiles  BKG
and SBKG must be time-invariant and laterally uniform. Since
wBKG = 0, (3) in that case leads to
BKG
and SBKG must be time-invariant and laterally uniform. Since
wBKG = 0, (3) in that case leads to
d/dz [K (d
(d BKG/dz)]
= 0 BKG/dz)]
= 0 |
(13) |
or once integrated over depth interval [z,h],
where F0 is a constant the
value of which is set by conditions at z = h. Over depth interval
[0,h], profiles of Kz and
is a constant the
value of which is set by conditions at z = h. Over depth interval
[0,h], profiles of Kz and  BKG
are thus linked; where K
BKG
are thus linked; where K grows
large near the seafloor, d
grows
large near the seafloor, d BKG/dz
must adjust appropriately. Equations (13)-(14) imply that to maintain a steady
BKG/dz
must adjust appropriately. Equations (13)-(14) imply that to maintain a steady
 BKG profile, the gradient flux of
BKG profile, the gradient flux of
 BKG must be balanced by a vertical
flux of opposite sign. Otherwise, background profiles would continually change,
making more difficult the resolution of small temperature anomalies caused only
by hydrothermal heating. Analogous arguments apply to SBKG.
BKG must be balanced by a vertical
flux of opposite sign. Otherwise, background profiles would continually change,
making more difficult the resolution of small temperature anomalies caused only
by hydrothermal heating. Analogous arguments apply to SBKG.
Above a boundary layer, background profiles of  and S were taken to be linear:
and S were taken to be linear:  =
= 
 (1 +
(1 + 

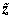 )
and S = S0 (1 +
)
and S = S0 (1 + 

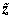 )
, where
)
, where 
 ,
S
,
S ,
, 
 ,
and
,
and 
 were given the values 1.6339°C, 34.616
were given the values 1.6339°C, 34.616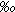 , 1.8925
× 10
, 1.8925
× 10 m
m ,
and -1.5751 × 10
,
and -1.5751 × 10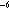 m
m and where
and where 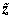 is height above the sea floor. These values are taken from linear least squares
fits of hydrographic profile data from the JDFR over the 2100-2400 m depth range,
profiles judged least affected by hydrothermal influences. Given those profiles
and (14), F0
is height above the sea floor. These values are taken from linear least squares
fits of hydrographic profile data from the JDFR over the 2100-2400 m depth range,
profiles judged least affected by hydrothermal influences. Given those profiles
and (14), F0 =
= 

 0K
0K (z = h) and F0S =
(z = h) and F0S =  2S
2S K
K (z = h). Since A
(z = h). Since A (z
= h) = 10
(z
= h) = 10 m
m s
s (equation (12)) and PR
= 1.0 (equation (10)), F0
(equation (12)) and PR
= 1.0 (equation (10)), F0 = 3.1 × 10
= 3.1 × 10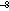 °C m
°C m s
s and F0S = 5.5
× 10
and F0S = 5.5
× 10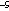
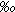 m
m s
s .
.
Integrating (4) with the A profile of (12) for PR = 1.0 results in the background profile
profile of (12) for PR = 1.0 results in the background profile
 BKG for 0 < z < h:
BKG for 0 < z < h:
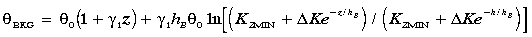 |
(15) |
having a well-mixed boundary layer (Figure 1b),
the height (~50 m) of which is determined by hB. In (15),
 K represents (KZMAX
- KZMIN). A like equation can be written for SBKG.
For z >> hB, the second term of (15) is negligible.
As with velocity,
K represents (KZMAX
- KZMIN). A like equation can be written for SBKG.
For z >> hB, the second term of (15) is negligible.
As with velocity,  BKG and SBKG
profiles (Figure 1b) are used to initialize fields
and provide upstream boundary profiles. Note in Figure
1 that where gradients of
BKG and SBKG
profiles (Figure 1b) are used to initialize fields
and provide upstream boundary profiles. Note in Figure
1 that where gradients of  and S
are large, velocity shear is small, and vice versa. This situation suppresses
shear instabilities that might otherwise develop. It follows that
and S
are large, velocity shear is small, and vice versa. This situation suppresses
shear instabilities that might otherwise develop. It follows that 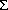 =
=  - 1000 has a similarly well-mixed boundary
layer (Figure 1b). Buoyancy frequency, N,
over depths 2100-2350 m is 7.9 × 10
- 1000 has a similarly well-mixed boundary
layer (Figure 1b). Buoyancy frequency, N,
over depths 2100-2350 m is 7.9 × 10 s
s .
.
A resolved Ekman boundary layer serves these purposes. It allows for directional
shear of flow that can influence plume dispersion. It reduces flow speed in
the boundary layer, flow that can affect entrainment of fluid into the plume
stem, particularly on the downstream side. Finally, a resolved boundary layer
is particularly important for plumes the B of which is not great enough to cause the plumes to rise distinctly above the
seafloor. Diffuse low-temperature sources of hydrothermal heat are instances
of that situation [Trivett
and Williams, 1994].
of which is not great enough to cause the plumes to rise distinctly above the
seafloor. Diffuse low-temperature sources of hydrothermal heat are instances
of that situation [Trivett
and Williams, 1994].
Boundary Conditions
Equations (1)-(10) were integrated over a rectangular domain with boundaries
open in x, cyclic in y, and fixed in z. Specifically, conditions
were
Lateral inflow boundary, x = X1
u = uBKG
v = vBKG
w = 0
 =
=  BKG BKG
S = SBKG.
|
(16) |
Lateral outflow boundary, x = X
uXXX = vXX
= wXX =  X
= SX = 0. X
= SX = 0. |
(17) |
Lower boundary, z = 0
u = v = w = 0
Kz [  / / z]
= F0 z]
= F0
Kz
[ S/ S/ z]
= F0S. z]
= F0S. |
(18) |
Upper boundary, z = h
 u/ u/ z
= z
=  v/ v/ z
= w = 0 z
= w = 0
Kz [  / / z]
= F0 z]
= F0
Kz
[ S/ S/ z]
= F0S. z]
= F0S. |
(19) |
Front and back boundaries, y = Y and y = Y
and y = Y
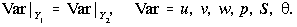 |
(20) |
Boundary conditions on p in the x and z directions were
taken in the manner of Harlow
and Welch [1965]. Cyclic conditions were used in the y
direction for all variables (u, v, w,  ,
S, and p) for two reasons: so the Ekman boundary layer of the
background flow would be uniform across the region of calculation and so plumes
could pass though y boundaries as if transparent. Cross-flow strength
and width of the solution domain were always large enough that the downstream
plume never filled the domain side to side, though in some cases the plume passed
through y boundaries. Boundary openness in the x direction was
essential to allow passage of heat and tracers out of the domain, which if prevented
would disallow any thermal equilibrium state from being reached. X direction
boundary conditions are those suggested by Johansson
[1993]. In these experiments, no absorbing layers [e.g.,
Clark and Farley, 1984] were used to damp waves.
,
S, and p) for two reasons: so the Ekman boundary layer of the
background flow would be uniform across the region of calculation and so plumes
could pass though y boundaries as if transparent. Cross-flow strength
and width of the solution domain were always large enough that the downstream
plume never filled the domain side to side, though in some cases the plume passed
through y boundaries. Boundary openness in the x direction was
essential to allow passage of heat and tracers out of the domain, which if prevented
would disallow any thermal equilibrium state from being reached. X direction
boundary conditions are those suggested by Johansson
[1993]. In these experiments, no absorbing layers [e.g.,
Clark and Farley, 1984] were used to damp waves.
Configuration and Parameter Values
As with background profiles, length scales, B ,
and background
,
and background  were chosen with regard to
conditions for chronic hydrothermal plumes at the JDFR. Equations were solved
in a Cartesian domain 640 × 320 × 300 m when U
were chosen with regard to
conditions for chronic hydrothermal plumes at the JDFR. Equations were solved
in a Cartesian domain 640 × 320 × 300 m when U was 1.5 cm s
was 1.5 cm s , but domain height was reduced
to 200 and then 150 m for increasingly larger U0 (Table 1).
Domain depth h was chosen for each U
, but domain height was reduced
to 200 and then 150 m for increasingly larger U0 (Table 1).
Domain depth h was chosen for each U so that plumes penetrated to ~ 0.5 h.
so that plumes penetrated to ~ 0.5 h.  x,
x,
 y,
y,  z,
z,
 t were 5, 5, and 9.4 (6.2 or 4.7) m,
and 15 s, respectively. N
t were 5, 5, and 9.4 (6.2 or 4.7) m,
and 15 s, respectively. N ,
Ny, Nz, and N
,
Ny, Nz, and N were 128, 64, 32, and 2000 (or 5760).
were 128, 64, 32, and 2000 (or 5760).
The source region was 10 × 10 m and was centered at the horizontal location
(x,y) = (-105, 0) m; source lateral dimension will hereafter be
represented by D. Individual hydrothermal vents have smaller surface
cross sections, but separate vents can be clustered in fields [Ginster
et al., 1994], or the hydrothermal source may be diffuse, like
the sulfide mounds described by Schultz
et al. [1992]. The intention here was to model plumes not from
a single vent, but from a small composite venting source or vent field. Resolving
a single small vent and its regional plume is beyond present computational resources.
Model source area was thus chosen to be representative of typical vent field
and sulfide mound surface areas. Despite having an extended area, the source
is nonetheless point-like in that rise height, hRISE, is very
much greater than D.
Source heat flux, Q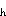 , was
set at 1.3 × 10
, was
set at 1.3 × 10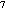 J s
J s (13 MW), a value chosen to cause maximum plume rise of ~200 m under reference
experiment conditions. Since buoyancy flux B
(13 MW), a value chosen to cause maximum plume rise of ~200 m under reference
experiment conditions. Since buoyancy flux B = g
= g Q
Q /
/
 /CP,
where
/CP,
where  is the thermal expansion coefficient
(7.3 × 10
is the thermal expansion coefficient
(7.3 × 10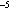 °C
°C ),
B
),
B was fixed at 2.1 × 10
was fixed at 2.1 × 10 m
m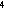 s
s . Buoyancy
flux density was consequently 2.1 × 10
. Buoyancy
flux density was consequently 2.1 × 10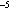 m
m s
s .
.
The value assigned QH is consistent with the wide range of
heat fluxes measured for single vents when extrapolated to a small vent field.
For 18 vents on the southern Juan de Fuca Ridge, Bemis
et al. [1993] estimated an average heat flux of 0.1-3.1 MW per
vent. Ginster
et al. [1994] indicated an average heat output of 3.1 MW for
single high-temperature vents on the southern JDFR and higher values on the
ridge's northerly Endeavor segment, where hydrothermal plumes can reach 300
m above the seafloor. There their estimated heat flux density of 0.139 MW m would, over a source area of 10 × 10 m, give a Q
would, over a source area of 10 × 10 m, give a Q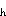 very much like the 13 MW heat flux value used in these calculations. Schultz
et al. [1992] estimated a heat flux of 58 MW from a 4 × 5 m sulfide
mound at Endeavor.
very much like the 13 MW heat flux value used in these calculations. Schultz
et al. [1992] estimated a heat flux of 58 MW from a 4 × 5 m sulfide
mound at Endeavor.
Calculations were made for a site latitude of 45°N. With the nonvertical component
of rotation set to zero, the rotation vector (
 ,
,

 ,
,

 )
was (0, 0, 5.14 × 10
)
was (0, 0, 5.14 × 10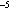 s
s );
an example of the effect of nonzero
);
an example of the effect of nonzero 
 [Garwood
et al., 1985] on a hydrothermal plume is given by Lavelle
[1995]. Mixing parameters were typically AHMIN
= 10
[Garwood
et al., 1985] on a hydrothermal plume is given by Lavelle
[1995]. Mixing parameters were typically AHMIN
= 10 m
m s
s and AVMIN = 10-4
m
and AVMIN = 10-4
m s
s .
CS was set to 0.2, and PR, the ratio of
turbulent viscosity to diffusivity, was given the value 1. Mixing length,
ls, was made equal to (
.
CS was set to 0.2, and PR, the ratio of
turbulent viscosity to diffusivity, was given the value 1. Mixing length,
ls, was made equal to ( x
x y
y z)1/3
[e.g.,
Reynolds, 1990]. Values for lS, CS,
and PR are not uniquely assignable, but values here are in
ranges commonly used. Sensitivity of results to these parameters can be found,
in part, in studies of axisymmetric plumes by Lavelle
and Baker [1994] and of plumes from line segment sources by Lavelle
[1995].
z)1/3
[e.g.,
Reynolds, 1990]. Values for lS, CS,
and PR are not uniquely assignable, but values here are in
ranges commonly used. Sensitivity of results to these parameters can be found,
in part, in studies of axisymmetric plumes by Lavelle
and Baker [1994] and of plumes from line segment sources by Lavelle
[1995].
Time and length scales pertinent to the development of convective plumes from
point and extended sources in rotating but otherwise quiescent background environments
may be found in the recent work of Jones
and Marshall [1993], Maxworthy
and Narimousa [1994], and Speer
and Marshall [1995]. For point sources and under stratified and
depth-unlimited conditions, the external set of three variables, B ,
f, and N, allows two length scales to be derived. The first, well
known from nonrotating conditions, is lN = (B
,
f, and N, allows two length scales to be derived. The first, well
known from nonrotating conditions, is lN = (B /N
/N )1/4
[e.g.,
Turner, 1973]. By replacing N by f, a second
length scale is uncovered: lf = (B
)1/4
[e.g.,
Turner, 1973]. By replacing N by f, a second
length scale is uncovered: lf = (B /f
3)1/4 [e.g.,
Speer and Marshall, 1995] or lROT = (B
/f
3)1/4 [e.g.,
Speer and Marshall, 1995] or lROT = (B /f
3)½, where B
/f
3)½, where B in the last equation is buoyancy flux density rather than total buoyancy flux
[Maxworthy
and Narimousa, 1994]. Atmospheric and laboratory observations
for plumes rising in nonrotating environments without cross flow have established
that maximum rise height, hRISE, scales like lN:
hRISE ~ 3.75 lN [e.g.,
Hanna et al., 1982]. An example in which lROT
was found to be relevant comes from rotating tank studies of Maxworthy
and Narimousa [1994] on brine convection. They found that once
a brine from a distributed (i.e., nonpoint) source reached a fluid depth of
the order of 12.7 lROT, convection transitioned from a three-dimensional
turbulent condition to one dominated by descending vortical columns. Length
scales such as l
in the last equation is buoyancy flux density rather than total buoyancy flux
[Maxworthy
and Narimousa, 1994]. Atmospheric and laboratory observations
for plumes rising in nonrotating environments without cross flow have established
that maximum rise height, hRISE, scales like lN:
hRISE ~ 3.75 lN [e.g.,
Hanna et al., 1982]. An example in which lROT
was found to be relevant comes from rotating tank studies of Maxworthy
and Narimousa [1994] on brine convection. They found that once
a brine from a distributed (i.e., nonpoint) source reached a fluid depth of
the order of 12.7 lROT, convection transitioned from a three-dimensional
turbulent condition to one dominated by descending vortical columns. Length
scales such as l and lROT
help organize experimental, observational, and occasionally numerical [e.g.,
Speer and Marshall, 1995; Lavelle
and Smith, 1996] results, but in all cases the coefficient of
scaling must be determined from data.
and lROT
help organize experimental, observational, and occasionally numerical [e.g.,
Speer and Marshall, 1995; Lavelle
and Smith, 1996] results, but in all cases the coefficient of
scaling must be determined from data.
Previous modeling work on hydrothermal megaplumes, which are caused by short-lived
thermal releases associated with episodic tectonic events [e.g.,
Embley et al., 1995], have confirmed the utility of those
scales in such cases. Speer
and Marshall [1995] used lf and the timescale
for Coriolis effects to be important, f -1, to scale rotational
velocities in the counterrotating vortices that should develop during megaplume
formation. Lavelle
and Baker [1994] and Speer
and Marshall [1995] found that l scales rise height as it does in the nonrotating case under typical benthic
ocean conditions, and Lavelle
[1995] has shown that the timescale for megaplumes reaching hRISE
is ~ 4N
scales rise height as it does in the nonrotating case under typical benthic
ocean conditions, and Lavelle
[1995] has shown that the timescale for megaplumes reaching hRISE
is ~ 4N . The fact that megaplumes
form quickly permits the modeling assumption of a quiescent background.
. The fact that megaplumes
form quickly permits the modeling assumption of a quiescent background.
In the case of chronically discharging hydrothermal plumes, the assumption
of a quiescent background environment is no longer tenable. Furthermore, these
more typical hydrothermal plumes are not products of ephemeral sources of heat.
They do not produce bottom-detached lenses of water, the geostrophic adjustment
of which Gill
[1981] and McWilliams
[1988] have studied. Consequently, one must not expect that such
plumes are associated with a Burger number ~1 nor expect that the description
of bent-over plumes should involve length scales l and lf, as is made clear below.
and lf, as is made clear below.
In the case of continuous discharging plumes in a cross flow, the set of external
variables from which length scales can be constructed is increased from three
to four: the variable U must
be added to the previous set. Generalized length scales that result from the
expanded set are B
must
be added to the previous set. Generalized length scales that result from the
expanded set are B (1+
(1+ )
N
)
N U
U (-3-4
(-3-4 ) and B
) and B (1+
(1+ )
f
)
f  U
U (-3-4
(-3-4 ).
When
).
When  = -1, advective length scales LNADV
= U
= -1, advective length scales LNADV
= U /N and LfADV
= U
/N and LfADV
= U /f emerge. When
/f emerge. When
 = -3/4, lN and lf
are recovered. But
= -3/4, lN and lf
are recovered. But  can take other values. Atmospheric
and laboratory observations of plume in a cross flow show that lN
(i.e.,
can take other values. Atmospheric
and laboratory observations of plume in a cross flow show that lN
(i.e.,  = -1) is not an appropriate scaling
for plume rise height, for example. Those data (and entrainment theory, e.g.,
Middleton
[1986]) point to a value for
= -1) is not an appropriate scaling
for plume rise height, for example. Those data (and entrainment theory, e.g.,
Middleton
[1986]) point to a value for  that
is more nearly -2/3, so that rise heights of plumes in cross flows scale like
lCROSS = [B
that
is more nearly -2/3, so that rise heights of plumes in cross flows scale like
lCROSS = [B /(U
/(U N
N )]1/3
[e.g,
Hanna et al., 1982], not like [B
)]1/3
[e.g,
Hanna et al., 1982], not like [B N
N ]1/4
as in cases without background flow. For plumes in a cross flow, it is only
through observations that the coefficient of scaling and indeed even the value
of
]1/4
as in cases without background flow. For plumes in a cross flow, it is only
through observations that the coefficient of scaling and indeed even the value
of  can be found. Neither l
can be found. Neither l or lf have demonstrated roles in the scaling of cross-flow
plume results.
or lf have demonstrated roles in the scaling of cross-flow
plume results.
Transverse width of the plume is an important measure of the likelihood of
counterrotating vortex pair development seen in studies of plume formation in
quiescent backgrounds [e.g.,
Speer, 1989]. But it is clear that the width of a plume transverse
to the cross-flow direction cannot scale like LNADV, LfADV,
l or lf,
except in the limit U
or lf,
except in the limit U
 0: plumes having the same source B
0: plumes having the same source B grow narrower with increasing U
grow narrower with increasing U ,
but none of those four scales permit plumes with that U0 dependence.
The width must be inversely proportional to some power of cross-flow velocity,
perhaps scaling as lCROSS. The same arguments can be made
that l
,
but none of those four scales permit plumes with that U0 dependence.
The width must be inversely proportional to some power of cross-flow velocity,
perhaps scaling as lCROSS. The same arguments can be made
that l and lf
play no role in setting plume height. For the cross-flow magnitudes studied
in this paper, plume width above the source is always much less than lf,
the size at which one might expect the Coriolis force to cause counterrotating
vortices in the manner previously predicted for plumes without background flow
[Lavelle
and Baker, 1994; Speer
and Marshall, 1995]. Balancing vertical and horizontal mass flux
at the top of the plume stem in simple calculations leads to that conclusion
too. For the smallest U0 studied in the paper, cross flow
overwhelms upstream density-driven flow in the plume cap above the source. With
U
and lf
play no role in setting plume height. For the cross-flow magnitudes studied
in this paper, plume width above the source is always much less than lf,
the size at which one might expect the Coriolis force to cause counterrotating
vortices in the manner previously predicted for plumes without background flow
[Lavelle
and Baker, 1994; Speer
and Marshall, 1995]. Balancing vertical and horizontal mass flux
at the top of the plume stem in simple calculations leads to that conclusion
too. For the smallest U0 studied in the paper, cross flow
overwhelms upstream density-driven flow in the plume cap above the source. With
U larger than the density-driven
upstream velocity in the plume cap, the plume bends forward. With U
larger than the density-driven
upstream velocity in the plume cap, the plume bends forward. With U and B
and B typical of chronic
hydrothermal discharge conditions, the cross-flow carries plume mass injected
to the level of neutral buoyancy away at a rate that prevents a cross-flow dimension
of the plume to approach lf there.
typical of chronic
hydrothermal discharge conditions, the cross-flow carries plume mass injected
to the level of neutral buoyancy away at a rate that prevents a cross-flow dimension
of the plume to approach lf there.
An interesting transition to the axisymmetric plume case should occur in a
sequence of plumes as U
 0. Then one can expect the plume to first develop an anvil shape, with some
upstream progression of the plume and some widening of the plume in the transverse
direction. At even smaller U
0. Then one can expect the plume to first develop an anvil shape, with some
upstream progression of the plume and some widening of the plume in the transverse
direction. At even smaller U ,
the plume must begin to take on all the conditions of plumes described in earlier
papers, including a counterrotating vortex pair. U
,
the plume must begin to take on all the conditions of plumes described in earlier
papers, including a counterrotating vortex pair. U ,
of course, drops out of the scaling arguments in this limit and l
,
of course, drops out of the scaling arguments in this limit and l and lf prevail. The study of that transition from cross flow
to axisymmetric plumes has not been undertaken, nor have enough cross-flow experiments
been run that the process of scaling confirmation analogous to those of Speer
and Marshall [1995] or Lavelle
and Smith [1996] is possible now.
and lf prevail. The study of that transition from cross flow
to axisymmetric plumes has not been undertaken, nor have enough cross-flow experiments
been run that the process of scaling confirmation analogous to those of Speer
and Marshall [1995] or Lavelle
and Smith [1996] is possible now.
Numerical Aspects
Momentum equations were centered differenced in space in energy conservation
form and leapfrogged in time. An Asselin [Asselin,
1972] filter having 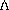 = 0.15 was
applied each time step to control temporal mode splitting. Integrations involved
solving a 3-D Poisson equation for p [Harlow
and Welch, 1965] on a staggered grid each time step using direct
method solvers HS3CRI and HS3CRT (R. Sweet, National Bureau of Standards, Boulder,
Colorado, 1985). Transport equations were forward time differenced. Their diffusion
terms were centered differenced in space, while advection terms were upstream
differenced but corrected each time step for unwanted numerical diffusion using
the procedure of Smolarkiewicz
[1983] and Smolarkiewicz
and Clark [1986]. Even in the presence of strong advection, upstream
differencing with correction can maintain relatively sharp property gradients
like those found at plume stem walls, while maintaining positive definiteness
of calculated quantities. The last attribute proves useful in eliminating the
occurrence of unphysically low property anomalies.
= 0.15 was
applied each time step to control temporal mode splitting. Integrations involved
solving a 3-D Poisson equation for p [Harlow
and Welch, 1965] on a staggered grid each time step using direct
method solvers HS3CRI and HS3CRT (R. Sweet, National Bureau of Standards, Boulder,
Colorado, 1985). Transport equations were forward time differenced. Their diffusion
terms were centered differenced in space, while advection terms were upstream
differenced but corrected each time step for unwanted numerical diffusion using
the procedure of Smolarkiewicz
[1983] and Smolarkiewicz
and Clark [1986]. Even in the presence of strong advection, upstream
differencing with correction can maintain relatively sharp property gradients
like those found at plume stem walls, while maintaining positive definiteness
of calculated quantities. The last attribute proves useful in eliminating the
occurrence of unphysically low property anomalies.
The accuracy of the model has been examined in the following ways. Requisite
conservation of mass, momentum, heat, salt, and energy was carefully checked
under a variety of forcing, as was symmetry (or antisymmetry) of all field variables
under symmetric forcing. Conditions for the independence of results from model
grid size were examined by Lavelle
and Baker [1994] using the axisymmetric realization of the model.
Results on sensitivity to the Smagorinsky coefficient and Prandtl number and
on the model relationship of plume rise height to buoyancy flux B0
are found in the same place. Additional sensitivity experiments, specifically
for rise height dependence on buoyancy flux and buoyancy frequency N,
were conducted for a line segment hydrothermal source rising into a quiescent
background environment [Lavelle,
1995]. That analysis demonstrated that the rise height of the model
scales as B 1/3 in
a quiescent background setting, as would be expected for that source configuration.
Model results on the scaling of plume rise height with cross-flow strength are
also encouraging. Atmospheric observations show plume rise height hRISE
depending on the cross-flow velocity U
1/3 in
a quiescent background setting, as would be expected for that source configuration.
Model results on the scaling of plume rise height with cross-flow strength are
also encouraging. Atmospheric observations show plume rise height hRISE
depending on the cross-flow velocity U as U
as U -
- ,
where
,
where  is ~1/3 [Hanna
et al., 1982]. As demonstrated later, this model shows a rise
height dependence on cross-flow velocity of U
is ~1/3 [Hanna
et al., 1982]. As demonstrated later, this model shows a rise
height dependence on cross-flow velocity of U -0.4,
with a coefficient of proportionality of similar magnitude to atmospheric cases.
-0.4,
with a coefficient of proportionality of similar magnitude to atmospheric cases.
Additional comparisons of model results to laboratory and field observations
have been made. The utility of the Smagorinksy-Lilly subgrid-scale turbulence
formulation was examined [Lavelle
and Smith, 1996] by comparing model with laboratory results [Fernando
and Ching, 1993] for a brine convection in a rotating tank. The
importance of self-generated turbulence during convection has long been recognized
[e.g.,
Priestly, 1956], and those numerical experiments in conjunction
with laboratory results have reconfirmed the view that time- and space-dependent
turbulence closure is essential. Furthermore, this model, under conditions of
cross flow in a nonrotating environment, produces flow patterns comparable to
the numerical results of Sykes
et al. [1986] and to experimental results they cite, as will
be described more fully below. Finally, hydrographic profiles from this model
for regions affected by chronic hydrothermal sources have the form and magnitude
of perturbed hydrographic profiles observed in the field (J. W. Lavelle et al.,
Effects of deep ocean hydrothermal discharge on near-source hydrography: Surrogate
field studies with a convective plume model, Pacific Marine Environmental Laboratory
contribution 1735, National Oceanic and Atmospheric Administration, Seattle,
Washington, 1996).
Model content vis-a-vis the simpler entrainment model of Morton
et al. [1956] was examined by computing the effective entrainment
coefficient from axisymmetric convective plume results [Lavelle
and Baker, 1994]. Horizontal velocities at the stem wall were
divided by the average vertical velocity at the same height in the stem, and
results were profiled as a function of height from the buoyancy source. Entrainment
profiles so derived showed the entrainment coefficient having a magnitude comparable
to that customarily used with integral theory ( ~ 0.1). Contrary to the assumption of entrainment theory the entrainment coefficient
was not constant with height, even becoming negative in the plume cap region
[Lavelle
and Baker, 1994]. The number of model checks and comparisons
to measurements enumerated here demonstrates how well tested this convection
model is.
~ 0.1). Contrary to the assumption of entrainment theory the entrainment coefficient
was not constant with height, even becoming negative in the plume cap region
[Lavelle
and Baker, 1994]. The number of model checks and comparisons
to measurements enumerated here demonstrates how well tested this convection
model is.
Results
Six model experiments are reported here. Discussion begins with a reference
case followed by contrasting results of perturbed cases (Table 1). Perturbed
cases refer to those at zero rotation rate ( = 0), null shear-dependent turbulent mixing intensity (CS
= 0, (6)), reduced horizontal background mixing (AHMIN = 10
= 0), null shear-dependent turbulent mixing intensity (CS
= 0, (6)), reduced horizontal background mixing (AHMIN = 10 m
m s
s , (4)),
and higher U
, (4)),
and higher U of 3 and 6 cm
s
of 3 and 6 cm
s . The three velocity cases to be compared
have R = wMAX /U
. The three velocity cases to be compared
have R = wMAX /U values of 6.6, 2.8, and 1.0, where wMAX is the computed maximum
upward velocity in the plume stem and U
values of 6.6, 2.8, and 1.0, where wMAX is the computed maximum
upward velocity in the plume stem and U is background flow velocity. Buoyancy dominates plume development for larger
R and cross flow dominates for smaller R. The parameter R
is often used to classify situations of jets entering cross flows, in which
case wMAX represents jet exit velocity. Sykes
et al. [1986] ran numerical experiments for jets that spanned
the ratio 2-8. Laboratory experiments of Ernst
et al. [1994] on buoyant jets in cross flows showed plume bifurcation
over the range R = 2-6.
is background flow velocity. Buoyancy dominates plume development for larger
R and cross flow dominates for smaller R. The parameter R
is often used to classify situations of jets entering cross flows, in which
case wMAX represents jet exit velocity. Sykes
et al. [1986] ran numerical experiments for jets that spanned
the ratio 2-8. Laboratory experiments of Ernst
et al. [1994] on buoyant jets in cross flows showed plume bifurcation
over the range R = 2-6.
Calculated fields in three dimensions and in time include 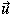 ,
p
,
p ,
,  ,
S, and AI. This paper focuses primarily on temperature
and velocity/vorticity fields near temporal equilibrium as a way to describe
differences caused by rotation, turbulence, and cross-flow speed.
,
S, and AI. This paper focuses primarily on temperature
and velocity/vorticity fields near temporal equilibrium as a way to describe
differences caused by rotation, turbulence, and cross-flow speed.
Reference Case
Figures 2 and 3
present cross sections through the reference experiment plume at 24 hours past
plume startup. With the given advection speed (U = 1.5 cm s
= 1.5 cm s ), the advection distance over
that time period is 3 times the distance (425 m) between source and outflow
boundary. By 24 hours, the plume is in equilibrium; heat flux through the outflow
boundary is equal to the heat input at the source. Even as early as 8 hours,
corresponding to an advection distance just past the outflow boundary, the plume
is in equilibrium around the source and near equilibrium at outflow, with outflow
heat flux already 80% of vent heat input.
), the advection distance over
that time period is 3 times the distance (425 m) between source and outflow
boundary. By 24 hours, the plume is in equilibrium; heat flux through the outflow
boundary is equal to the heat input at the source. Even as early as 8 hours,
corresponding to an advection distance just past the outflow boundary, the plume
is in equilibrium around the source and near equilibrium at outflow, with outflow
heat flux already 80% of vent heat input.
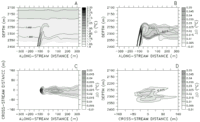
Figure 2. Plume distributions for the reference case (experiment 21,
Table 1) at t = 24 hours. The cross-stream direction is y and
the along-stream direction is x. (a)  on the plane y = 0; (b)
on the plane y = 0; (b) 
 on the plane y = 0; (c)
on the plane y = 0; (c) 
 on the plane z = 2280 m; (d)
on the plane z = 2280 m; (d) 
 on the plane x = 320 m. All contours are in degrees Celsius.
on the plane x = 320 m. All contours are in degrees Celsius.
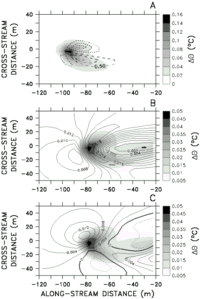
Figure 3. Velocity, 
 ,
and relative vorticity patterns for the reference case (experiment 21, Table
1) at t = 24 hours. (a)
,
and relative vorticity patterns for the reference case (experiment 21, Table
1) at t = 24 hours. (a) 
 (shaded) and
(shaded) and  z nondimensionalized
by U
z nondimensionalized
by U /D (contoured)
at z = 2350 m (z/D = 5); (b)
/D (contoured)
at z = 2350 m (z/D = 5); (b) 
 (shaded) and u velocity (contoured) at z = 2280 (z/D =
12); (c)
(shaded) and u velocity (contoured) at z = 2280 (z/D =
12); (c) 
 (shaded) and v velocity (contoured) at z = 2280 (z/D
= 12). Velocity is in meters per second.
(shaded) and v velocity (contoured) at z = 2280 (z/D
= 12). Velocity is in meters per second.
Contours of  (Figure
2a) show the effect of hydrothermal heat release on the surrounding environment.
Isotherms are drawn down into the source region. The inverted J-shaped isotherm
and a plume stem bent ~13° with respect to the vertical evidence the effects
of background flow. The well-defined stem has lateral
(Figure
2a) show the effect of hydrothermal heat release on the surrounding environment.
Isotherms are drawn down into the source region. The inverted J-shaped isotherm
and a plume stem bent ~13° with respect to the vertical evidence the effects
of background flow. The well-defined stem has lateral  gradients as large as 6.8 × 10
gradients as large as 6.8 × 10 °C m
°C m .
Relatively steep gradients such as these are not numerically easy to preserve;
their occurrence in these calculations results from the use of the upstream
corrected advection scheme of Smolarkiewicz
and Clark [1986]. Downstream internal waves above the height
of the convection column with wavelength of ~140-170 m are also evident in Figure
2a. These are associated with internal waves in u and w velocities
with amplitudes of ~0.2 and 0.6 cm s
.
Relatively steep gradients such as these are not numerically easy to preserve;
their occurrence in these calculations results from the use of the upstream
corrected advection scheme of Smolarkiewicz
and Clark [1986]. Downstream internal waves above the height
of the convection column with wavelength of ~140-170 m are also evident in Figure
2a. These are associated with internal waves in u and w velocities
with amplitudes of ~0.2 and 0.6 cm s , respectively.
Lees waves in the atmosphere resulting from convective motion have been modeled
by Hauf
and Clark [1989] and are used to good advantage by glider pilots
[Kuettner
et al., 1987]. A possible explanation for their occurrence is
that a convection column can act, in part, like a hill, forcing environmental
flow over and around, but further numerical experimentation is required to be
unequivocal about the cause in this setting.
, respectively.
Lees waves in the atmosphere resulting from convective motion have been modeled
by Hauf
and Clark [1989] and are used to good advantage by glider pilots
[Kuettner
et al., 1987]. A possible explanation for their occurrence is
that a convection column can act, in part, like a hill, forcing environmental
flow over and around, but further numerical experimentation is required to be
unequivocal about the cause in this setting.
The  anomaly,
anomaly, 
 =
=  -
-  BKG,
contoured in units of 0.005°C (Figure 2b), better
shows the maximum rise of the plume to be 180 m. For the given combination of
U
BKG,
contoured in units of 0.005°C (Figure 2b), better
shows the maximum rise of the plume to be 180 m. For the given combination of
U and B
and B ,
the plume overshoots the neutral density level. Yet flow is strong enough, with
the given source buoyancy and stratification, that the overshoot is small, and
strong enough that no limb of the plume appears upstream of the source. For
fixed B
,
the plume overshoots the neutral density level. Yet flow is strong enough, with
the given source buoyancy and stratification, that the overshoot is small, and
strong enough that no limb of the plume appears upstream of the source. For
fixed B , an upstream limb
can be expected as U
, an upstream limb
can be expected as U is reduced
[e.g.,
Ernst et al., 1994], and full plume symmetry about the then-vertical
convection axis must occur when U
is reduced
[e.g.,
Ernst et al., 1994], and full plume symmetry about the then-vertical
convection axis must occur when U = 0 [e.g.,
Lavelle, 1995]. In all cases reported here, U
= 0 [e.g.,
Lavelle, 1995]. In all cases reported here, U is sufficiently large (
is sufficiently large (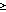 1.5 cm/s) that neither
upstream nor significant cross-stem plume growth occurs. Flows in and around
the stem and plume cap region, which result from the superposition of background
and convective flows, are also much different than flows expected in and around
convective plumes rising into a quiescent background environment [e.g.,
Lavelle and Baker, 1994].
1.5 cm/s) that neither
upstream nor significant cross-stem plume growth occurs. Flows in and around
the stem and plume cap region, which result from the superposition of background
and convective flows, are also much different than flows expected in and around
convective plumes rising into a quiescent background environment [e.g.,
Lavelle and Baker, 1994].
Vertical velocities in the stem reach maxima of 0.1 m s in this example. The plume overshoots the equilibrium level and causes a slight
positive density anomaly
in this example. The plume overshoots the equilibrium level and causes a slight
positive density anomaly 
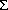 in the region above the stem. Just downstream of the positive
in the region above the stem. Just downstream of the positive 
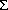 region, flow has a downward directed component with vertical velocities of as
much as 0.03 m s
region, flow has a downward directed component with vertical velocities of as
much as 0.03 m s . The local maximum of
. The local maximum of 
 centered near x = 50 m (Figure 2b) is
at the terminal end of this downward directed flow. Note that
centered near x = 50 m (Figure 2b) is
at the terminal end of this downward directed flow. Note that 
 > 0.02 °C extends only several hundred meters downstream because of lateral
dispersion. Since resolving
> 0.02 °C extends only several hundred meters downstream because of lateral
dispersion. Since resolving 

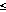 0.01 °C in field data is difficult, a single
hydrothermal source of the given size in this stratification environment ought
to be difficult to detect thermally beyond several hundred meters from the vent
source.
0.01 °C in field data is difficult, a single
hydrothermal source of the given size in this stratification environment ought
to be difficult to detect thermally beyond several hundred meters from the vent
source.
A planar view of the same plume at 120 m above the bottom (z = 2280
m, Figure 2c) shows the small aspect ratio of
the plume for the given cross-flow strength. At the outflow boundary, the plume
(i.e., the 0.005°C isopleth) at this depth is ~100 m wide. Growth of the plume
in the flow transverse direction is limited by the downstream transport of plume
material. The local maximum centered at x = 75 m (Figure
2c) is the same local maximum evident in Figure
2b, the consequence of initial plume overshoot with subsequent downward
advection. Computations without rotation show planar distributions with perfect
symmetry about the y = 0 axis. The slight asymmetry of the pattern of
Figure 2c is thus caused by rotation, a topic
to be taken up more fully later. No undesirable outflow boundary layer is apparent
in Figures 2a-2c, evidence that supports Johansson's
[1993] prescription for boundary conditions.
At the outflow boundary (x = 320 m), the equilibrium plume shows a maximum
core 
 of 0.015°C
(Figure 2d). The plume (i.e., 0.005°C isopleth)
has maximum width of ~200 m, about half the width of the computational domain
(320 m). Cyclic boundary conditions in the y direction allow transport
through the side walls of the calculational region, but little
of 0.015°C
(Figure 2d). The plume (i.e., 0.005°C isopleth)
has maximum width of ~200 m, about half the width of the computational domain
(320 m). Cyclic boundary conditions in the y direction allow transport
through the side walls of the calculational region, but little  -distribution
contamination by adjoining cyclic domains is apparent. A wider computational
domain width would be necessitated if smaller U
-distribution
contamination by adjoining cyclic domains is apparent. A wider computational
domain width would be necessitated if smaller U were used. A test experiment was performed to examine the change in results
due to quadrupling the domain width. In that case the y-direction resolution
was coarsened to 10 m, but all other aspects of the calculations were left intact.
Results were not significantly different from those shown here. In consideration
of computational costs, most experiments were run with the 320-m domain width.
were used. A test experiment was performed to examine the change in results
due to quadrupling the domain width. In that case the y-direction resolution
was coarsened to 10 m, but all other aspects of the calculations were left intact.
Results were not significantly different from those shown here. In consideration
of computational costs, most experiments were run with the 320-m domain width.
Circulation in the region of the plume stem and above is considerably different
from that predicted for point source convection in otherwise quiescent environments
[e.g.,
Lavelle and Baker, 1994]. In the high 
 -gradient
region near the source,
-gradient
region near the source, 
 contours (shaded, Figure 3a) are kidney- or horseshoe-shaped,
as found numerically, for example, of plumes in nonrotating environments by
Sykes
et al. [1986]. The same authors cite numerous laboratory observations
of the same effect. While much of the upstream fluid enters the stem, there
is also some spatial acceleration of flow around the stem. Downstream of the
stem there is a u-velocity minimum and beyond that is a reconvergence
of the stem-separated flow. The flow patterns result in a counterrotating
contours (shaded, Figure 3a) are kidney- or horseshoe-shaped,
as found numerically, for example, of plumes in nonrotating environments by
Sykes
et al. [1986]. The same authors cite numerous laboratory observations
of the same effect. While much of the upstream fluid enters the stem, there
is also some spatial acceleration of flow around the stem. Downstream of the
stem there is a u-velocity minimum and beyond that is a reconvergence
of the stem-separated flow. The flow patterns result in a counterrotating  z
couplet (contours, Figure 3a) with a
z
couplet (contours, Figure 3a) with a  z
maximum on the right (referenced to the downstream direction) and a minimum
on the left, at the downstream end of the
z
maximum on the right (referenced to the downstream direction) and a minimum
on the left, at the downstream end of the 
 anomalies. Such a counterrotating
anomalies. Such a counterrotating 
 couplet at the downstream edge of a jet entering cross flow was noted by Turner
[1960] and observed by Moussa
et al. [1977], for example. Besides the asymmetry caused by rotation
(Figure 3a), the
couplet at the downstream edge of a jet entering cross flow was noted by Turner
[1960] and observed by Moussa
et al. [1977], for example. Besides the asymmetry caused by rotation
(Figure 3a), the  z
pair is also much like the one found numerically by Sykes
et al. [1986] for jets in nonrotating, unstratified cross flows.
Not shown is the perturbation pressure (p') distribution, which has two
local minima of comparable size located asymmetrically about y = 0 and
slightly downstream of the
z
pair is also much like the one found numerically by Sykes
et al. [1986] for jets in nonrotating, unstratified cross flows.
Not shown is the perturbation pressure (p') distribution, which has two
local minima of comparable size located asymmetrically about y = 0 and
slightly downstream of the 
 isopleth tips.
isopleth tips.
The kidney-shaped pattern of 
 extends from the seafloor to the levels of neutral buoyancy. At z = 2280
m, the pattern of
extends from the seafloor to the levels of neutral buoyancy. At z = 2280
m, the pattern of 
 in the stem region (shaded, Figures 3b and 3c)
also has two lobes, the right lobe being larger. Asymmetry about y =
0 is again the consequence of Coriolis forces. Superimposed on the
in the stem region (shaded, Figures 3b and 3c)
also has two lobes, the right lobe being larger. Asymmetry about y =
0 is again the consequence of Coriolis forces. Superimposed on the 
 distributions are isopleths of u (Figure 3b)
and v (Figure 3c). With background flow
at 0.015 m s
distributions are isopleths of u (Figure 3b)
and v (Figure 3c). With background flow
at 0.015 m s , Figure
3b shows a region of reduced u ahead of the convection column and
a region of near-zero u some 20 m downstream. The v distribution
(Figure 3c) shows maxima to both side of the
column, but much higher v in the direction of positive y. Downstream,
the signs of the two v lobes reverse to allow the reconvergence of the
flow that was deflected to either side of the column. Though Figure
3 bears evidence that the Coriolis force does affect plume structure, the
simple anticyclonic flow for the upper plume predicted when convection occurs
in a quiescent background environment [Lavelle
and Baker, 1994] no longer occurs. Additional differences in
plume structure with and without rotation are discussed in the following section.
, Figure
3b shows a region of reduced u ahead of the convection column and
a region of near-zero u some 20 m downstream. The v distribution
(Figure 3c) shows maxima to both side of the
column, but much higher v in the direction of positive y. Downstream,
the signs of the two v lobes reverse to allow the reconvergence of the
flow that was deflected to either side of the column. Though Figure
3 bears evidence that the Coriolis force does affect plume structure, the
simple anticyclonic flow for the upper plume predicted when convection occurs
in a quiescent background environment [Lavelle
and Baker, 1994] no longer occurs. Additional differences in
plume structure with and without rotation are discussed in the following section.
The Nonrotating Case
A nonrotational case was next examined. To isolate direct effects of rotation,
the u profile of Figure 1a was taken as
the along-stream background current, and cross-stream v was taken to
be zero in experiment 22. Using (11), a 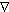 P
P profile consistent with those velocity profiles but unique to the nonrotating
case was determined. The resulting
profile consistent with those velocity profiles but unique to the nonrotating
case was determined. The resulting 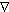 P
P was used to force ambient cross flow (Table 1). Using the
was used to force ambient cross flow (Table 1). Using the  P
P of experiment 21 when
of experiment 21 when  = 0 would have resulted
in a uBKG profile with a much thicker boundary layer.
= 0 would have resulted
in a uBKG profile with a much thicker boundary layer.
The primary difference in 
 caused by rotation is the absence of distributional symmetry about y
= 0; rise height, overshoot, and magnitudes are otherwise similar in a general
sense. As expected, u and v too are symmetrical about y
= 0 in experiment 22 (Figures 4a and 4b) but
not in experiment 21 (Figures 4c and 4d). To
allow easier comparison of these results with those of Sykes
et al. [1986], velocities and distances in Figure
4 have been non-dimensionalized by U
caused by rotation is the absence of distributional symmetry about y
= 0; rise height, overshoot, and magnitudes are otherwise similar in a general
sense. As expected, u and v too are symmetrical about y
= 0 in experiment 22 (Figures 4a and 4b) but
not in experiment 21 (Figures 4c and 4d). To
allow easier comparison of these results with those of Sykes
et al. [1986], velocities and distances in Figure
4 have been non-dimensionalized by U and D.
and D.
Figure 4. Comparison of rotating (experiment 21) and nonrotating (experiment
22) cases. Velocity u nondimensionalized by U on the plane z = 2380 m (z/D = 2) when
on the plane z = 2380 m (z/D = 2) when  = 0 (Figure 4a) and when
= 0 (Figure 4a) and when 
 0 (Figure 4c).
Velocity v nondimensionalized by U
0 (Figure 4c).
Velocity v nondimensionalized by U on the plane z = 2380 m (z/D = 2) when
on the plane z = 2380 m (z/D = 2) when  = 0 (Figure 4b) and when
= 0 (Figure 4b) and when 
 0 (Figure 4d).
For
0 (Figure 4d).
For  = 0,
= 0, 
 on the plane x = -60 m (x/D = 4) (Figure
4e) and nondimensional u on the plane x = -60 m (x/D
= 4) (Figure 4f).
on the plane x = -60 m (x/D = 4) (Figure
4e) and nondimensional u on the plane x = -60 m (x/D
= 4) (Figure 4f).
Figures 4a ( = 0) and 4c (
= 0) and 4c (
 0) show u in the vicinity of the
source at a vertical distance of z/D = 2, where z is distance
from the seafloor. When
0) show u in the vicinity of the
source at a vertical distance of z/D = 2, where z is distance
from the seafloor. When  = 0, u is nearly
doubled (U/U
= 0, u is nearly
doubled (U/U = 1.9)
on both sides of the rising plume as background flow, in part, sweeps around
the ascending fluid column. The bulk of the upstream flow is undeflected; after
entering the column, u momentum is displaced vertically, with the result
that little of the u momentum entering upstream is found downstream at
z levels where the stem is well-defined. The u velocity immediately
downstream of the stem is just greater than zero, although flow of small size
(u < 0) occurs in the boundary layer (z/D < 2) and at some
sites above z/D = 10. Though the possibility of downstream reverse flow
(u < 0) must depend on boundary layer thickness and strength of upward
convection, the general result, that nearly all entrainment into the stem occurs
from the upstream side of plumes under similar forcing conditions, is likely
not to be significantly altered.
= 1.9)
on both sides of the rising plume as background flow, in part, sweeps around
the ascending fluid column. The bulk of the upstream flow is undeflected; after
entering the column, u momentum is displaced vertically, with the result
that little of the u momentum entering upstream is found downstream at
z levels where the stem is well-defined. The u velocity immediately
downstream of the stem is just greater than zero, although flow of small size
(u < 0) occurs in the boundary layer (z/D < 2) and at some
sites above z/D = 10. Though the possibility of downstream reverse flow
(u < 0) must depend on boundary layer thickness and strength of upward
convection, the general result, that nearly all entrainment into the stem occurs
from the upstream side of plumes under similar forcing conditions, is likely
not to be significantly altered.
In the rotating case (Figure 4c), reverse flow
(u < 0) occurs on the left side of the convection column (y
> 0), while larger along-stream flow (u/U = 2.4) occurs on the right (y < 0). This asymmetry helps shape the
= 2.4) occurs on the right (y < 0). This asymmetry helps shape the

 distribution
of, for example, Figure 3a. The region of flow
affected is small. Consequently, field observations of u enhancement
near a heat source may prove difficult, if only because of the small size of
the region involved.
distribution
of, for example, Figure 3a. The region of flow
affected is small. Consequently, field observations of u enhancement
near a heat source may prove difficult, if only because of the small size of
the region involved.
Magnitude of the transverse velocity, |v| , reaches ~0.6U in both cases (Figures 4b and 4d). For
in both cases (Figures 4b and 4d). For  = 0, maximum |v| occurs nearly twice as far downstream as |
= 0, maximum |v| occurs nearly twice as far downstream as |
 |
maxima, which occur at the downstream edge of the stem. The v convergence
(Figure 4b) results in u values again
having magnitudes ~U
|
maxima, which occur at the downstream edge of the stem. The v convergence
(Figure 4b) results in u values again
having magnitudes ~U within
a distance of 5D downstream of x = 0. The effect of
within
a distance of 5D downstream of x = 0. The effect of 
 0 on v (Figure
4d) is to skew distributions across the plane of symmetry (y = 0)
so maximum |v| occurs slightly farther downstream than does maximum |-v|.
Magnitudes of v at this z level are little changed by rotation.
0 on v (Figure
4d) is to skew distributions across the plane of symmetry (y = 0)
so maximum |v| occurs slightly farther downstream than does maximum |-v|.
Magnitudes of v at this z level are little changed by rotation.
For cases when R = 4 and R = 8, Sykes
et al. [1986] provide distributions of a passive scalar and u
on the cross section x/D = 4. While their study of jets involved
neither background stratification nor a boundary layer, their results show horseshoe-shaped
patterns for the scalar (as in Figure 4e) and
u distributions with a low velocity core underlying a higher velocity
high region (as in Figure 4f). Results here show
larger vertical gradients above the 
 core (Figure 4e) and maximum u velocities
the distribution of which drapes less over the sides of the lower u core
(Figure 4f) than it does in the results of Sykes
et al. [1986]. Those differences undoubtedly reflect the presence
of background stratification. In none of the panels of Figure
4 is the full domain of computation shown.
core (Figure 4e) and maximum u velocities
the distribution of which drapes less over the sides of the lower u core
(Figure 4f) than it does in the results of Sykes
et al. [1986]. Those differences undoubtedly reflect the presence
of background stratification. In none of the panels of Figure
4 is the full domain of computation shown.
Relative vorticity distributions allow a comparison to the results of Sykes
et al. [1986] as well. Nondimensionalized stream-wise vorticity

 in the source region at z/D = 2 appears as a counterrotating couplet
(Figure 5a); even during plume development (t
< 1 hour) the couplet at this level has the indicated strength and shape.
Low p
in the source region at z/D = 2 appears as a counterrotating couplet
(Figure 5a); even during plume development (t
< 1 hour) the couplet at this level has the indicated strength and shape.
Low p is found just downstream of extremal
is found just downstream of extremal
 x sites. If
x sites. If 
 contours were superimposed,
contours were superimposed,  x
extrema would be seen to be just downstream of the
x
extrema would be seen to be just downstream of the 
 center. When
center. When 
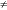 0, the axis separating the two counterrotating vortices of the couplet is oriented
clockwise of the x axis, but magnitudes are comparable to those of the
0, the axis separating the two counterrotating vortices of the couplet is oriented
clockwise of the x axis, but magnitudes are comparable to those of the
 = 0 case. Sykes
et al. [1986] found distributions of
= 0 case. Sykes
et al. [1986] found distributions of 
 that are similar in both length scale and intensity at this height. The similarity
is not surprising, in that at z/D = 2 the background environment
is well mixed (Figures 1a-1b) and by this time
(t = 8.3 hours) conditions in the stem have long ago reached equilibrium.
The pattern (Figure 5a) is primarily the consequence
of the
that are similar in both length scale and intensity at this height. The similarity
is not surprising, in that at z/D = 2 the background environment
is well mixed (Figures 1a-1b) and by this time
(t = 8.3 hours) conditions in the stem have long ago reached equilibrium.
The pattern (Figure 5a) is primarily the consequence
of the  w/
w/ y
contribution to
y
contribution to  x and, for
fixed x, error function-like distributions of w in the y
direction across the plume stem; the other term contributing to
x and, for
fixed x, error function-like distributions of w in the y
direction across the plume stem; the other term contributing to  x,
x,
 v/
v/ z,
is less than 10% the size of
z,
is less than 10% the size of  w/
w/ y.
y.
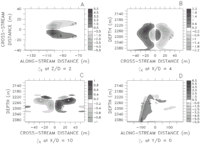
Figure 5. Relative vorticity, nondimensionalized by U /D,
about the x axis,
/D,
about the x axis, 
 ,
when
,
when  = 0 on the planes (a) z = 2380
(z/D = 2), (b) x = -60 m (x/D = 4), and (c)
x = 0 (x/D = 10). (d) Relative vorticity, nondimensionalized
by U
= 0 on the planes (a) z = 2380
(z/D = 2), (b) x = -60 m (x/D = 4), and (c)
x = 0 (x/D = 10). (d) Relative vorticity, nondimensionalized
by U /D, about the
y axis,
/D, about the
y axis, 
 ,
on the plane y = 0.
,
on the plane y = 0.
Downstream, the distribution of  x
grows in complexity. For example, on the plane x/D = 4,
x
grows in complexity. For example, on the plane x/D = 4, 
 has two pairs of counterrotating cells (Figure 5b).
The underlying velocity field is like that measured by Fearn
and Weston [1974] for a jet entering a cross flow. It is the
w distribution, similar to Figure 4e,
once differentiated (i.e.,
has two pairs of counterrotating cells (Figure 5b).
The underlying velocity field is like that measured by Fearn
and Weston [1974] for a jet entering a cross flow. It is the
w distribution, similar to Figure 4e,
once differentiated (i.e.,  w/
w/ y),
much more than the distribution of
y),
much more than the distribution of  v/
v/ x,
that determines the form of
x,
that determines the form of 
 .
At this x location,
.
At this x location,  x
again resembles that found by Sykes
et al. [1986]. At x/D = 10, where negative w
at the level of neutral buoyancy is a response to the initial plume overshoot
(Figure 3a),
x
again resembles that found by Sykes
et al. [1986]. At x/D = 10, where negative w
at the level of neutral buoyancy is a response to the initial plume overshoot
(Figure 3a), 
 is preponderantly negative on the right side and positive on the left (Figure
5c). No similar result could be expected for jets in homogenous flow because
then no vertical overshoot is possible. Stratification also broadens and flattens
the
is preponderantly negative on the right side and positive on the left (Figure
5c). No similar result could be expected for jets in homogenous flow because
then no vertical overshoot is possible. Stratification also broadens and flattens
the  x distribution at this
distance.
x distribution at this
distance.
In experiment 22 ( = 0), initially only
= 0), initially only 
 is nonzero, and then only in the boundary layer, because background shear is
at first unidirectional. Both
is nonzero, and then only in the boundary layer, because background shear is
at first unidirectional. Both 
 and
and 
 quickly develop, however, and
quickly develop, however, and 
 is substantially changed as convectively forced flow develops. On the plane
y = 0, for example, singlet
is substantially changed as convectively forced flow develops. On the plane
y = 0, for example, singlet 
 becomes a couplet extending much higher into the water column (Figure
5d) with extremal values (6.5 units) that dwarf original magnitudes (-0.65
units). The distribution of
becomes a couplet extending much higher into the water column (Figure
5d) with extremal values (6.5 units) that dwarf original magnitudes (-0.65
units). The distribution of 
 in Figure 5d is also determined by the distribution
of w across the stem region:
in Figure 5d is also determined by the distribution
of w across the stem region:  w/
w/ x,
the significant factor determining
x,
the significant factor determining 
 ,
is positive entering the stem on the upstream side and negative exiting the
stem downstream. Sykes
et al. [1986] and Klemp
[1987], among others, have analyzed the growth of vorticity components
as convection occurs, so a full discussion of that time development is unnecessary
to repeat here. Klemp
[1987] shows that when cross-stream vorticity is present, it is tilted
and drawn up by buoyancy driven flow during thunderstorm development to initiate
a
,
is positive entering the stem on the upstream side and negative exiting the
stem downstream. Sykes
et al. [1986] and Klemp
[1987], among others, have analyzed the growth of vorticity components
as convection occurs, so a full discussion of that time development is unnecessary
to repeat here. Klemp
[1987] shows that when cross-stream vorticity is present, it is tilted
and drawn up by buoyancy driven flow during thunderstorm development to initiate
a  z couplet (e.g., Figure
3a). Schlesinger
[1980] suggests that no initial shear is needed for all three
z couplet (e.g., Figure
3a). Schlesinger
[1980] suggests that no initial shear is needed for all three  components to develop, but tilting by advection is a primary means of growth
for downstream
components to develop, but tilting by advection is a primary means of growth
for downstream  components during storm development.
components during storm development.
Dominance of  x and
x and 
 by one of the horizontal derivatives of w points to the certainty of
development of both relative vorticity components starting at the time buoyancy
is first generated because vertical velocity is created by buoyancy from startup.
For example, without cross flow the distribution of w in the budding
stem would be Gaussian in both lateral directions, and the first derivative
of w would lead to counterrotating vorticity pairs in both x and
y directions, i.e.,
by one of the horizontal derivatives of w points to the certainty of
development of both relative vorticity components starting at the time buoyancy
is first generated because vertical velocity is created by buoyancy from startup.
For example, without cross flow the distribution of w in the budding
stem would be Gaussian in both lateral directions, and the first derivative
of w would lead to counterrotating vorticity pairs in both x and
y directions, i.e.,  x and
x and
 y. Clearly no cross-stream
or stream-wise vorticity is needed initially when buoyancy forcing is present
to generate
y. Clearly no cross-stream
or stream-wise vorticity is needed initially when buoyancy forcing is present
to generate  x and
x and 
 .
Just as clearly does
.
Just as clearly does  z production
begin at the same time: as the convection column first deflects a fraction of
the background flow to both sides, flow that subsequently converges downstream,
distributions of u and v (Figures 4a-4d)
are created that once differentiated lead to nonzero
z production
begin at the same time: as the convection column first deflects a fraction of
the background flow to both sides, flow that subsequently converges downstream,
distributions of u and v (Figures 4a-4d)
are created that once differentiated lead to nonzero  z.
Production of all components of
z.
Production of all components of  must occur
at any location where buoyancy has begun to disturb background flow.
must occur
at any location where buoyancy has begun to disturb background flow.
Sensitivity to Mixing Strength
To gauge sensitivity of results to subgrid-scale mixing, two additional experiments
were performed. In the first, dependence of mixing on shear (equation (6)) was
eliminated by setting CS = 0, so only constant mixing coefficients
controlled turbulent diffusion (experiment 23). Those background mixing coefficients
had relatively small values AZMIN (10 m2 s
m2 s ) and AHMIN
(10
) and AHMIN
(10 m2 s
m2 s ),
as indicated earlier. In another experiment (experiment 26), CS
was left at 0.2 so that AI (equation (6)) would be a significant
factor in mixing in the stem region, where shears are larger, but the value
of AHMIN that controls lateral mixing outside that region
was reduced by a factor of 10. In this case AHMIN is smaller
(10
),
as indicated earlier. In another experiment (experiment 26), CS
was left at 0.2 so that AI (equation (6)) would be a significant
factor in mixing in the stem region, where shears are larger, but the value
of AHMIN that controls lateral mixing outside that region
was reduced by a factor of 10. In this case AHMIN is smaller
(10 m
m s
s )
than even AZMAX (equation (12)). In reference experiment 21,
AI in the plume stem was typically 10-20 × 10
)
than even AZMAX (equation (12)). In reference experiment 21,
AI in the plume stem was typically 10-20 × 10 m2 s
m2 s . With a small value in experiment
26, AHMIN had little influence on mixing in the stem region
and much reduced influence beyond. Effects of stirring by nonlinear advection
beyond the convection region are thus highlighted in experiment 26.
. With a small value in experiment
26, AHMIN had little influence on mixing in the stem region
and much reduced influence beyond. Effects of stirring by nonlinear advection
beyond the convection region are thus highlighted in experiment 26.
Results at t = 8.3 hours for the three cases are shown in Figure
6. In both panels, 
 isopleths are provided as solid lines (experiment 23), dotted lines (experiment
26), or shaded regions (experiment 21). Both experiments with reduced turbulent
mixing show
isopleths are provided as solid lines (experiment 23), dotted lines (experiment
26), or shaded regions (experiment 21). Both experiments with reduced turbulent
mixing show  anomalies with greater spatial
variability. Three plumes along y = 0 (Figure 6a)
show that there is no substantial difference in the equilibrium level of the
plumes. Using height of maximum
anomalies with greater spatial
variability. Three plumes along y = 0 (Figure 6a)
show that there is no substantial difference in the equilibrium level of the
plumes. Using height of maximum 
 averaged over each section in the downstream interval 200 < x <
320 m as indicator, average rise heights were 136, 125, and 122 m for experiments
21, 23, and 26, respectively (Table 1). Thus reduced lateral mixing leads to
only slightly smaller rise heights. On the other hand, when time development
of the plumes is examined, the starting pulse of anomalous
averaged over each section in the downstream interval 200 < x <
320 m as indicator, average rise heights were 136, 125, and 122 m for experiments
21, 23, and 26, respectively (Table 1). Thus reduced lateral mixing leads to
only slightly smaller rise heights. On the other hand, when time development
of the plumes is examined, the starting pulse of anomalous  water rose to a height greater by 27 m in the case of smallest stem viscosity
(experiment 23) compared to the case of largest viscosity (experiment 21). Earlier
work by Lavelle
and Baker [1994] for plumes without cross flow had shown higher
rise heights with less stem mixing. Present results agree only for the initial
interval of rise to the level of neutral buoyancy, but not in the longer term.
The explanation must lie in differences in entrainment when cross flow is present.
In the cross flow case, background flow is forced into the plume stem region
on the upstream side, while without cross flow, entrainment is caused by convection
alone and occurs omnidirectionally.
water rose to a height greater by 27 m in the case of smallest stem viscosity
(experiment 23) compared to the case of largest viscosity (experiment 21). Earlier
work by Lavelle
and Baker [1994] for plumes without cross flow had shown higher
rise heights with less stem mixing. Present results agree only for the initial
interval of rise to the level of neutral buoyancy, but not in the longer term.
The explanation must lie in differences in entrainment when cross flow is present.
In the cross flow case, background flow is forced into the plume stem region
on the upstream side, while without cross flow, entrainment is caused by convection
alone and occurs omnidirectionally.
Figure 6. 
 for experiments that differ only in the subgrid-scale parameterization (Table
1). Results are represented by dotted contours for experiment 26 (AHMIN
= 10 cm
for experiments that differ only in the subgrid-scale parameterization (Table
1). Results are represented by dotted contours for experiment 26 (AHMIN
= 10 cm s
s ),
solid contours for experiment 23 (CS = 0), and shaded contours
for experiment 21, the reference case. (a) Cross sections for y = 0,
(b) cross sections for z = 2280 m. All contours are in degrees Celsius
at 8.3 hours.
),
solid contours for experiment 23 (CS = 0), and shaded contours
for experiment 21, the reference case. (a) Cross sections for y = 0,
(b) cross sections for z = 2280 m. All contours are in degrees Celsius
at 8.3 hours.
When viewed on the horizontal plane z = 2280 m, plumes of experiments
23 and 26 show larger lateral downstream spread than in the reference experiment
(Figure 6b). Counterintuitively, smaller mixing
coefficients either locally in the stem (experiment 23) or globally (experiment
26) cause greater lateral dispersion. Using the 0.005°C 
 isopleth to designate a plume edge, widths averaged over 200 < x <
320 m for the three experiments were 90, 188, and 155 m, respectively. In experiment
26, that same
isopleth to designate a plume edge, widths averaged over 200 < x <
320 m for the three experiments were 90, 188, and 155 m, respectively. In experiment
26, that same 
 edge shows signs of wispiness, as if Helmholtz shear instabilities were occurring.
edge shows signs of wispiness, as if Helmholtz shear instabilities were occurring.
Statistics of  z within the
downstream plume (
z within the
downstream plume (
 > 0.005°C, x > 100 m ) show experiment 26 having larger relative
vorticity. In experiment 26,
> 0.005°C, x > 100 m ) show experiment 26 having larger relative
vorticity. In experiment 26,  z
was more patchy downstream of the source. Mean values of |
z
was more patchy downstream of the source. Mean values of | z|
for the three experiments were 1.4 ×, 1.2 ×, and 2.9 × 10
z|
for the three experiments were 1.4 ×, 1.2 ×, and 2.9 × 10 s
s , while the standard deviation of |
, while the standard deviation of |
 |
for experiment 26 is twice as large as for the other experiments. This suggests
that resolved stirring rather than unresolved mixing is more significant as
a dispersion process in experiment 26 than in the others. Thus reduced turbulent
mixing in the far field, i.e., smaller AHMIN, allows stronger
small-scale stirring, which in turn leads to more widespread plume dispersal.
|
for experiment 26 is twice as large as for the other experiments. This suggests
that resolved stirring rather than unresolved mixing is more significant as
a dispersion process in experiment 26 than in the others. Thus reduced turbulent
mixing in the far field, i.e., smaller AHMIN, allows stronger
small-scale stirring, which in turn leads to more widespread plume dispersal.
Differences in velocities also are apparent with changes in turbulent mixing
intensity. In the stem, w maxima are smallest with full mixing (experiment
21) and largest when CS = 0 (experiment 23). Downstream negative
w are 40% larger in experiment 23 than experiment 21. Times series show
that differences are much more than just changes in magnitude. Animations of

 fields show
source heat, while steadily discharged at the seafloor, being pulsed to higher
levels when mixing is small (experiments 23 and 26) but not when mixing is higher
(experiment 21). Time series sampled at a site 120 m above and 27.5 m downstream
of the source (Figure 7) show, in comparison,
that
fields show
source heat, while steadily discharged at the seafloor, being pulsed to higher
levels when mixing is small (experiments 23 and 26) but not when mixing is higher
(experiment 21). Time series sampled at a site 120 m above and 27.5 m downstream
of the source (Figure 7) show, in comparison,
that 
 quickly
grows to a value of 0.06°C in all three experiments as the plume front passes
but thereafter they are quite different. For largest mixing (experiment 21),
quickly
grows to a value of 0.06°C in all three experiments as the plume front passes
but thereafter they are quite different. For largest mixing (experiment 21),

 smoothly
seeks an equilibrium level. In experiments 23 and 26, on the other hand,
smoothly
seeks an equilibrium level. In experiments 23 and 26, on the other hand, 
 values oscillate with periods of ~1300 s. The w time series at this location
shows similar frequency content. Buoyancy period, based on the linear region
of the
values oscillate with periods of ~1300 s. The w time series at this location
shows similar frequency content. Buoyancy period, based on the linear region
of the  profile (Figure
1b), is 1265 s. The oscillation period from model results is only a coarse
estimate because model data were sampled only every 300 s. Since the amplitude
of
profile (Figure
1b), is 1265 s. The oscillation period from model results is only a coarse
estimate because model data were sampled only every 300 s. Since the amplitude
of 
 oscillations
is nearly 0.03°C in experiment 26 (Figure 7),
field observations of
oscillations
is nearly 0.03°C in experiment 26 (Figure 7),
field observations of  very near to hydrothermal
heat sources at intervals of 1 min or less might be able to distinguish different
mixing coefficient regimes.
very near to hydrothermal
heat sources at intervals of 1 min or less might be able to distinguish different
mixing coefficient regimes.
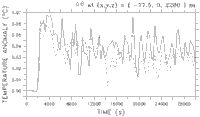
Figure 7. Time series of 
 at a fixed point in the plume stem (x/D = 2.25, y = 0,
z/D = 12). The dotted line represents the experiment of largest
subgrid-scale mixing (experiment 21), while the other two have reduced background
mixing (dashed line, experiment 26) or shear independent mixing (solid line,
experiment 23).
at a fixed point in the plume stem (x/D = 2.25, y = 0,
z/D = 12). The dotted line represents the experiment of largest
subgrid-scale mixing (experiment 21), while the other two have reduced background
mixing (dashed line, experiment 26) or shear independent mixing (solid line,
experiment 23).
Changes in Cross-Flow Strength
Effects of cross-flow strength were examined by increasing U from 1.5 cm s
from 1.5 cm s in experiment 21, to 3 and
6 cm s
in experiment 21, to 3 and
6 cm s in experiments 24 and 25, while all
other conditions were held fixed. That sequence of three experiments has R
= wMAX/Uo values of 6.6, 2.8, and 1.0, respectively,
where wMAX is maximum upward stem velocity determined empirically
from results of each experiment. This range of R is comparable to that
examined by Sykes
et al. [1986] and is approximately the range over which Ernst
et al. [1994], in laboratory experiments, found significant changes
in the character of buoyant jets in cross flows.
in experiments 24 and 25, while all
other conditions were held fixed. That sequence of three experiments has R
= wMAX/Uo values of 6.6, 2.8, and 1.0, respectively,
where wMAX is maximum upward stem velocity determined empirically
from results of each experiment. This range of R is comparable to that
examined by Sykes
et al. [1986] and is approximately the range over which Ernst
et al. [1994], in laboratory experiments, found significant changes
in the character of buoyant jets in cross flows.
Plumes bend increasingly with increasing cross-flow strength, as expected (Figures
8a and 8d); in all panels of Figure 8 the
dotted line represents the 
 = 0.005°C isotherm of experiment 21. Rise heights, hRISE,
based on the location of maximum
= 0.005°C isotherm of experiment 21. Rise heights, hRISE,
based on the location of maximum 
 in vertical sections at the outflow boundary for each of the three experiments
are 136, 97, and 77 m, respectively, the last value representing the higher
of two
in vertical sections at the outflow boundary for each of the three experiments
are 136, 97, and 77 m, respectively, the last value representing the higher
of two 
 maxima
(Figure 8f). On the basis of those three values
alone, a best fit of hRISE to U
maxima
(Figure 8f). On the basis of those three values
alone, a best fit of hRISE to U gives hRISE
gives hRISE  U
U -0.40.
Extensive atmospheric observations have led to the canonical form hRISE
= 2.6 [B
-0.40.
Extensive atmospheric observations have led to the canonical form hRISE
= 2.6 [B /(U
/(U N
N )]1/3
for bent-over plumes in the stratified atmosphere [e.g.,
Hanna et al., 1982], where hRISE refers
to distance between source level and the vertical midpoint of the plume downstream
of the source. Thus, for atmospheric cases, hRISE
)]1/3
for bent-over plumes in the stratified atmosphere [e.g.,
Hanna et al., 1982], where hRISE refers
to distance between source level and the vertical midpoint of the plume downstream
of the source. Thus, for atmospheric cases, hRISE  U
U -0.33. The similarity
of U
-0.33. The similarity
of U dependence for these
model results and atmospheric data is encouraging, though the paucity of model
realizations, the difficulty of defining rise height when the distribution has
more than a single maximum (Figure 8f), and the
difference in rise height definitions between this and the atmospheric case
are all causes for caution.
dependence for these
model results and atmospheric data is encouraging, though the paucity of model
realizations, the difficulty of defining rise height when the distribution has
more than a single maximum (Figure 8f), and the
difference in rise height definitions between this and the atmospheric case
are all causes for caution.
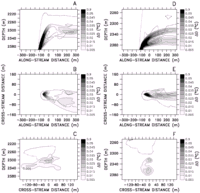
Figure 8. Contours of 
 in degrees Celsius at 8.3 hours for experiment 24 (U
in degrees Celsius at 8.3 hours for experiment 24 (U = 0.03 m s
= 0.03 m s , Table 1) at (a) y = 0,
(b) z = 2320 m, (c) x = 300 m, and for experiment 25 (U
, Table 1) at (a) y = 0,
(b) z = 2320 m, (c) x = 300 m, and for experiment 25 (U = 0.06 m s
= 0.06 m s , Table 1) at (d) y = 0,
(e) z = 2360 m, and (f) x = 300 m. The dotted contour in each
panel represents the 0.005°C isopleth for the reference case (experiment 21).
, Table 1) at (d) y = 0,
(e) z = 2360 m, and (f) x = 300 m. The dotted contour in each
panel represents the 0.005°C isopleth for the reference case (experiment 21).
Unexpectedly, plumes of experiments 24 and 25 have voids in the downstream

 distributions.
For experiment 23 (R = 2.8) this occurs just downstream of the stem,
but the branches merge again farther downstream (Figure
8a). In experiment 26 (R = 1.0), branching occurs farther from the
stem region and extends to the outflow boundary (Figure
8d). No such
distributions.
For experiment 23 (R = 2.8) this occurs just downstream of the stem,
but the branches merge again farther downstream (Figure
8a). In experiment 26 (R = 1.0), branching occurs farther from the
stem region and extends to the outflow boundary (Figure
8d). No such 
 voids were seen in experiment 21 (R = 6.6, Figure
2).
voids were seen in experiment 21 (R = 6.6, Figure
2).
In neither of the two cases is branching simple. For R = 2.8, a section
for z = 2320 m (Figure 8b) shows that
the 
 void
does not extend laterally all the way across the plume. The core region of highest
void
does not extend laterally all the way across the plume. The core region of highest
 gradients has a more exaggerated kidney shape
than in experiment 21, but only the right branch spawns material downstream
at this level; the left branch is truncated. A sequence of horizontal sections
shows the
gradients has a more exaggerated kidney shape
than in experiment 21, but only the right branch spawns material downstream
at this level; the left branch is truncated. A sequence of horizontal sections
shows the 
 void to be tubular with the principal axis of the tube skewed from the vertical.
The irregularly shaped tube cuts through the plume wall, here defined as the
void to be tubular with the principal axis of the tube skewed from the vertical.
The irregularly shaped tube cuts through the plume wall, here defined as the
 = 0.005°C isopleth, on the left-hand side
below z = 2310 m, creating the left-side void seen in Figure
8b. Above z = 2310 m, the right-side wall of the plume is interrupted.
In the x direction near the stem,
= 0.005°C isopleth, on the left-hand side
below z = 2310 m, creating the left-side void seen in Figure
8b. Above z = 2310 m, the right-side wall of the plume is interrupted.
In the x direction near the stem,  is
continuous on the right-hand side below z = 2310 m and continuous on
the left-hand side above. Beyond x = ~100 m, the plume has no voids.
At x = 300 m (Figure 8c) it is wider than
high, with two local
is
continuous on the right-hand side below z = 2310 m and continuous on
the left-hand side above. Beyond x = ~100 m, the plume has no voids.
At x = 300 m (Figure 8c) it is wider than
high, with two local 
 maxima. The rightmost maximum evidently buds from the lower right-hand limb
of the kidney-shaped region, while the upper maximum buds from the higher-rising
left-hand limb.
maxima. The rightmost maximum evidently buds from the lower right-hand limb
of the kidney-shaped region, while the upper maximum buds from the higher-rising
left-hand limb.
For the plume rising into the strongest cross flow (R = 1.0, experiment
25), the picture of a top-to-bottom bifurcation suggested by Figure
8d is also not complete. The planar view (Figure
8e) shows a plume with a strong right-hand limb and a stunted left-hand
limb at z = 2360 m. A sequence of horizontal slices shows that the left-hand
limb is favored below z = 2380 m and the right-hand limb is favored above.
The left-hand limb is attached to the seafloor and extends to x = ~200
m before disappearing; the attachment is in part caused by the location of the
source at the seafloor, but effects of the low vertical resolution of the boundary
layer by the model cannot be discounted. The right-hand limb splits vertically
but does not completely separate; the section at x = 300 m (Figure
8f) shows that the bifurcation in Figure 8d
was apparent only; the two vertically aligned maxima are connected. The plume
would be earmarked as distinctly bifurcated only if 
 = 0.005°C were too small an anomaly to be observed. Thus an observational threshold
can affect judgement as to whether a plume has bifurcated or not. This result
should also serve warning that two
= 0.005°C were too small an anomaly to be observed. Thus an observational threshold
can affect judgement as to whether a plume has bifurcated or not. This result
should also serve warning that two 
 maxima in a single vertical profile in a hydrothermal region may not mean that
two venting sources, each with different B
maxima in a single vertical profile in a hydrothermal region may not mean that
two venting sources, each with different B ,
are nearby.
,
are nearby.
Distributions of 
 within these plumes might seem peculiar if it were not for field and laboratory
observations that confirm that plumes from buoyant jets can bifurcate. Scorer
[1959] noted the occurrence of plume bifurcation in ordinary chimney
plumes. Observations of bifurcating industrial stack plumes are exemplified
in the report of Fanaki
[1975]. Volcanic plume bifurcations are summarized by Ernst
et al. [1994]. Several laboratory experiments of Wu
et al. [1988] on buoyant jets in unstratified flows led to vertical
bifurcation of the kind seen in experiment 25 (Figure
8f), though in the laboratory it was a source configuration skewed with
respect to flow direction rather than environmental rotation or shear in cross
flow that broke plume symmetry about the y axis.
within these plumes might seem peculiar if it were not for field and laboratory
observations that confirm that plumes from buoyant jets can bifurcate. Scorer
[1959] noted the occurrence of plume bifurcation in ordinary chimney
plumes. Observations of bifurcating industrial stack plumes are exemplified
in the report of Fanaki
[1975]. Volcanic plume bifurcations are summarized by Ernst
et al. [1994]. Several laboratory experiments of Wu
et al. [1988] on buoyant jets in unstratified flows led to vertical
bifurcation of the kind seen in experiment 25 (Figure
8f), though in the laboratory it was a source configuration skewed with
respect to flow direction rather than environmental rotation or shear in cross
flow that broke plume symmetry about the y axis.
Mechanisms that cause jet or plume bifurcations are not completely understood,
though observations have pinpointed some conditions under which bifurcation
is likely to occur. In cases of jets entering unstratified flows, the ratio
R has been used to classify results. Ernst
et al. [1994] saw buoyant laboratory jets that clearly bifurcated
when R fell in the range 2-6, but bifurcation was blurred or did not
occur at higher or lower R values. In model plumes addressed here, bifurcation
occurred but was not complete when R = 1.0 and 2.8, but did not occur
when R = 6.6. Ernst
et al. [1994] noted that sharp density interfaces, orientation
of a jet orifice with respect to the flow, and latent heat release all can influence
the occurrence of a bifurcation. In the case of convection during severe storms,
Klemp
and Wilhelmson [1978] showed that vertical shear of environmental
winds and downdraft caused by precipitation are important to the storm splitting
and divergence process. On the basis of results reported here, it is appropriate
to add rotation, background stratification, and boundary layer shear to the
list of possible factors affecting plume bifurcation. The large number of potential
factors involved, however, will likely make the identification of conditions
and causes leading to the bifurcation of hydrothermal plumes difficult.
Conclusions
Initial parameter sensitivity experiments made with a three-dimensional time-dependent
hydrodynamical model of buoyancy-driven plumes in sheared, stratified cross
flows have shown a number of effects on plumes caused by differences in rotation
rates, turbulent mixing intensity, and cross-flow strength. While the context
of the work here is for hydrothermal plumes rising several hundreds of meters
into the benthic ocean as the result of chronic releases of magmatic heat from
vents along submarine ridge crests, the model has considerable generality. Important
features of the model include: inflow and outflow boundaries that allow passage
of fluid, heat, and salt without the development of unrealistic along-stream
boundary layers; bottom Ekman boundary layers for velocity, temperature, and
salinity; time- and space-dependent turbulent mixing; and the use of an advection
scheme for  and S that maintains a well-defined
plume stem with its accompanying large lateral property gradients.
and S that maintains a well-defined
plume stem with its accompanying large lateral property gradients.
The model shows that most of the cross-flowing fluid encountering the stem
is entrained into it on the upstream side of the plume. In the parameter regime
examined, little entrainment into the stem occurs on the lee side of the stem.
The rising column of fluid also deflects some cross flow around it, thus acting
in part like an obstruction. The result is vertical counterrotating vortices
on each side of the plume stem, long identified in studies of plumes and jets
as the  z couplet. The rising
column of fluid also leads to internal waves downstream at or above the level
of neutral buoyancy.
z couplet. The rising
column of fluid also leads to internal waves downstream at or above the level
of neutral buoyancy.
Distributions of velocities around the heat source have properties, in a general
sense, like those earlier observed for jets injected into cross streams in nonrotating
environments: vorticity couplets in all three coordinate directions develop
in the plume stem, then follow the plume to its level of neutral buoyancy, and
ultimately decline in strength with downstream distance. Rotation, as expected,
breaks the cross-stream symmetry or antisymmetry of the distributions.
Intensity of turbulent mixing changes width and wispiness of plumes, with higher
stem viscosity/diffusivity resulting in steadier plumes with smaller downstream
lateral spread. Though the source is steady, turbulent mixing coefficients of
reduced size allow oscillations in  and w
at the buoyancy frequency, which are suppressed when the strength of turbulent
mixing is increased.
and w
at the buoyancy frequency, which are suppressed when the strength of turbulent
mixing is increased.
For fixed buoyancy and increasing cross-flow strength, model plumes encompass
instances of plume bifurcation. When the ratio R of maximum upward velocity
to cross-flow strength was 2.8, the plume had a columnar void just downstream
of the plume stem but none at greater distance. When R = 1.0, bifurcation
was incomplete but vertical sections at increasing distance from the stem showed
vertically bimodal 
 distributions. When R = 6.6, no plume bifurcation was observed. Initial
experiments are too few in number to identify mechanisms that cause bifurcations,
but results suggest that this model is a tool that can contribute to that understanding.
distributions. When R = 6.6, no plume bifurcation was observed. Initial
experiments are too few in number to identify mechanisms that cause bifurcations,
but results suggest that this model is a tool that can contribute to that understanding.
Acknowledgments. Support for this work comes from the NOAA
VENTS program. Encouragement to pursue this modeling work by VENTS colleagues
is appreciated. Contribution 1687 from NOAA/Pacific Marine Environmental Laboratory.
�
References
Asselin, R. A., Frequency filters for time integrations, Mon. Weather Rev.,
100, 487-490, 1972.
Baker, E. T., C. R. German, and H. Elderfield, Hydrothermal plumes over spreading-center
axes: global distributions and geological inferences, in Seafloor Hydrothermal
Systems: Physical, Chemical, Biological, and Geochemical Interactions, Geophys.
Monogr. Ser., vol. 91, pp. 47-71, edited by S. E. Humphris, R. A. Zierenberg,
L. S. Mullineaux, and R. E. Thomson, AGU, Washington, D.C., 1995.
Baker, E. T., Y. J. Chen, and J. Phipps Morgan, The relationship between near-axis
hydrothermal cooling and the spreading rate of mid-ocean ridges, Earth Planet.
Sci. Lett., 142, 137-145, 1996.
Bemis, K. G., R. P. von Herzen, and M. J. Mottl, Geothermal heat flux from
hydrothermal plumes on the Juan de Fuca Ridge, J. Geophys. Res., 98,
6351-6365, 1993.
Cannon, G. A., D. J. Pashinski, and M. R. Lemon, Middepth flow near hydrothermal
venting sites on the southern Juan de Fuca Ridge, J. Geophys. Res.,
96, 12,815-12,831, 1991.
Clark, T. L., and R. D. Farley, Severe downslope windstorm calculations in
two and three spatial dimensions using anelastic interactive grid nesting: A
possible mechanism for gustiness, J. Atmos. Sci., 41, 329-350,
1984.
Claus, R. W., and S. P. Vanka, Multigrid calculations of a jet in crossflow,
J. Propul. Power, 8, 425-431, 1992.
Davidson, G. A., Simultaneous trajectory and dilution predictions from a simple
integral plume model, Atmos. Environ., 23, 341-349, 1989.
Delaney, J. R., V. Robigou, R. E. McDuff, and M. K. Tivey, Geology of a vigorous
hydrothermal system on the Endeavour Segment, Juan de Fuca Ridge, J. Geophys.
Res., 97, 19,663-19,682, 1992.
Embley, R. W., W. W. Chadwick Jr., I. R. Johnson, D. A. Butterfield, and E.
T. Baker, Initial results of the rapid response to the 1993 CoAxial Event: Relationships
between hydrothermal and volcanic processes, Geophys. Res. Lett., 22,
143-146, 1995.
Ernst, G. G. J., J. P. Davis, and R. S. J. Sparks, Bifurcation of volcanic
plumes in a crosswind, Bull. Volcanol., 56, 159-169, 1994.
Fanaki, F. H., Experimental observations of a bifurcated buoyant plume, Boundary
Layer Meteorol., 9, 479-495, 1975.
Fearn, R., and R. P. Weston, Vorticity associated with a jet in a crossflow,
AIAA J., 12, 1666-1671, 1974.
Feely, R. A., G. J. Massoth, E. T. Baker, G. T. Lebon, and T. L. Geiselman,
Tracking the dispersal of hydrothermal plumes from the Juan de Fuca Ridge using
suspended matter compositions, J. Geophys. Res., 97, 3457-3468,
1992.
Fernando, H. J. S., and C. Y. Ching, Effects of background rotation of turbulent
line plumes, J. Phys. Oceanogr., 23, 2125-2129, 1993.
Fofonoff, N. P., and R. C. Millard Jr., Algorithms for computation of fundamental
properties of seawater, UNESCO Tech. Pap. Mar. Sci. 44, 53 pp.,
UNESCO, Paris, 1983.
Fox, C. G., W. E. Radford, R. P. Dziak, T.-K. Lau, H. Matasumoto, and A. E.
Schreiner, Acoustic detection of a seafloor spreading episode on the Juan de
Fuca Ridge using military hydrophone arrays, Geophys. Res. Lett., 22,
131-134, 1995.
Galperin, B., and S. A. Orszag (eds.), Large Eddy Simulation of Complex
Engineering and Geophysical Flows, 600 pp., Cambridge Univ. Press, New York,
1993.
Garrett, C., Mixing in the ocean interior, Dyn. Atmos. Oceans, 3,
239-265, 1979.
Garwood, R., P. Gallacher, and P. Muller, Wind direction and equilibrium mixed-layer
depth: General theory, J. Phys. Oceanogr., 15, 1325-1331, 1985.
Gill, A. E., Homogeneous intrusions in a rotating stratified fluid, J. Fluid
Mech., 103, 275-296, 1981.
Ginster, U., M. J. Mottl, and R. P. Von Herzen, Heat flux from black smokers
on the Endeavour and Cleft segments, Juan de Fuca Ridge, J. Geophys. Res.,
99, 4937-4950, 1994.
Golay, M. W., Numerical modeling of buoyant plumes in a turbulent, stratified
atmosphere, Atmos. Environ., 16, 2373-2381, 1982.
Hanna, S. R., G. A. Briggs, and R. P. Hosker Jr., Handbook of Atmospheric
Diffusion, 102 pp., Tech. Inf. Cent., U.S. Dep. of Energy, Washington, D.C.,
1982. (Available from Natl. Tech. Inf. Serv., Springfield, Va.)
Harlow, F. H., and J. E. Welch, Numerical calculation of time-dependent viscous
incompressible flow of fluid with a free surface, Phys. Fluids, 8(12),
2182-2189, 1965.
Hauf, T., and T. L. Clark, Three-dimensional numerical experiments on convectively
forced internal gravity waves, Q. J. R. Meteorol. Soc., 115, 309-333,
1989.
Johansson, B. C. V., Boundary conditions for open boundaries for the incompressible
Navier-Stokes equation, J. Comput. Phys., 105, 233-251, 1993.
Jones, H., and J. Marshall, Convection with rotation in a neutral ocean: A
study of open ocean convection, J. Phys. Oceanogr., 23, 1009-1039, 1993.
Klemp, J. B., Dynamics of tornadic thunderstorms, Annu. Rev. Fluid Mech.,
19, 369-402, 1987.
Klemp, J. B., and R. B. Wilhelmson, The simulation of three-dimensional convective
storm dynamics, J. Atmos. Sci., 35, 1070-1096, 1978.
Kuettner, J. P., P. A. Hildebrand, and T. L. Clark, Convection waves: Observations
of gravity wave systems over convectively active boundary layers, Q. J. R.
Meteorol. Soc., 113, 445-467, 1987.
Lavelle, J. W., The initial rise of a hydrothermal plume from a line segment
source: Results from a three-dimensional numerical model, Geophys. Res. Lett.,
22, 159-162, 1995.
Lavelle, J. W., and E. T. Baker, A numerical study of local convection in the
benthic ocean induced by episodic hydrothermal discharges, J. Geophys. Res.,
99, 16,065-16,080, 1994.
Lavelle, J. W., and D. C. Smith IV, Effects of rotation on convective plumes
from line segment sources, J. Phys. Oceanogr., 26, 863-872, 1996.
Lilly, D. K., On the numerical simulation of buoyant convection, Tellus,
14, 148-172, 1962.
List, E. J., Turbulent jets and plumes, Annu. Rev. Fluid Mech., 14,
189-212, 1982.
Lupton, J., and H. Craig, A major  He source
in hydrothermal plumes in the Galapagos Rift, Nature, 267, 603-604,
1977.
He source
in hydrothermal plumes in the Galapagos Rift, Nature, 267, 603-604,
1977.
Mason, P. J., Large-eddy simulation of the convective atmospheric boundary
layer, J. Atmos. Sci., 46, 1492-1516, 1989.
Mason, P. J., Large eddy simulation: A critical review of the technique, Q.
J. R. Meteorol. Soc., 120, 1-26, 1994.
Massoth, G. J., E. T. Baker, J. E. Lupton, R. A. Feely, D. A. Butterfield,
K. L. Von Damm, K. K. Roe, and G. T. Lebon, Temporal and spatial variability
of hydrothermal manganese and iron at Cleft segment, Juan de Fuca Ridge, J.
Geophys. Res., 99, 4905-4923, 1994.
Massoth, G. J., E. T. Baker, R. A. Feely, D. A. Butterfield, R. E. Embley,
J. E. Lupton, R. E. Thomson, and G. A. Cannon, Observations of manganese and
iron at the CoAxial seafloor eruption site, Juan de Fuca Ridge, Geophys.
Res Lett., 22, 151-154, 1995.
Maxworthy, T., and S. Narimousa, Unsteady, turbulent convection into a homogeneous,
rotating fluid, with oceanographic applications, J. Phys. Oceanogr., 24,
865-887, 1994.
McWilliams, J. C., Vortex generation through balanced adjustment, J. Phys.
Oceanogr., 18, 1178-1192, 1988.
Middleton, J. H., The rise of forced plumes in a stably stratified cross flow,
Boundary Layer Meteorol., 36, 187-200, 1986.
Middleton, J. H., and R. E. Thomson, Modelling the rise of hydrothermal plumes,
Can. Tech. Rep. Hydrogr. Ocean Sci. Ser. 69, 14 pp., Dep. of Fish. and
Oceans, Inst. of Ocean Sci., Sydney, B.C., Canada, 1986.
Morton, B. R., G. I. Taylor, and J. S. Turner, Turbulent gravitational convection
from maintained and instantaneous sources, Proc. R. Soc. London A,
234, 1-23, 1956.
Mottl, M. J., F. J. Sansone, C. G. Wheat, J. A. Resing, E. T. Baker, and J.
E. Lupton, Manganese and methane in hydrothermal plumes along the East Pacific
Rise, 8°40 to 11°50
to 11°50 N,
Geochim. Cosmochim. Acta, 59, 4147-4165, 1995.
N,
Geochim. Cosmochim. Acta, 59, 4147-4165, 1995.
Moussa, J. M., J. W. Trischka, and S. Eskinazi, The near field in the mixing
of a round jet with a cross stream, J. Fluid. Mech., 80, 49-80,
1977.
Priestly, C. H. B., A working theory of bent-over plumes of hot gas, Q.
J. R. Meteorol. Soc., 82, 165-176, 1956.
Reynolds, W. C., The potential and limitations of direct and large scale eddy
simulations, in Whither Turbulence? Turbulence at the Crossroads, edited
by J. L. Lumley, pp. 313-343, Springer-Verlag, New York, 1990.
Schlesinger, R. E., A three-dimensional numerical model of an isolated thunderstorm,
II, Dynamics of updraft splitting and mesovortex couplet evolution, J. Atmos.
Sci., 37, 395-420, 1980.
Schultz, A., J. R. Delaney, and R. E. McDuff, On the partitioning of heat flux
between diffuse and point source seafloor venting, J. Geophys. Res.,
97, 12,299-12,314, 1992.
Scorer, R. S., The behavior of chimney plumes, Int. J. Air Water Pollut.,
1, 198-220, 1959.
Slawson, P. R., and G. T. Csanady, On the mean path of buoyant, bent-over chimney
plumes, J. Fluid Mech., 28, 311-322, 1967.
Smagorinsky, J., General circulation experiments with the primitive equations,
I, The basic experiment, Mon. Weather Rev., 91, 99-152, 1963.
Smagorinsky, J., Some historical remarks on the use of nonlinear viscosities,
in Large Eddy Simulation of Complex Engineering and Geophysical Flows,
edited by B. Galperin and S. A. Orsag, pp. 3-36, Cambridge Univ. Press, New
York, 1993.
Smolarkiewicz, P. K., A fully multidimensional positive definite advection
transport algorithm with small implicit diffusion, J. Comput. Phys.,
54, 325-362, 1983.
Smolarkiewicz, P. K., and T. L. Clark, Numerical simulation of the evolution
of a three-dimensional field of cumulus clouds, I, Model description, comparison
with observations, and sensitivity studies, J. Atmos. Sci., 42,
502-522, 1985.
Smolarkiewicz, P. K., and T. L. Clark, The multidimensional positive definite
advection transport algorithm: Further development and applications, J. Comput.
Phys., 67, 396-438, 1986.
Speer, K. G., A forced baroclinic vortex around a hydrothermal plume, Geophys.
Res. Lett., 16, 461-464, 1989.
Speer, K. G., and J. Marshall, The growth of convective plumes at seafloor
hot springs, J. Mar. Res., 53, 1025-1057, 1995.
Sykes, R. L., W. S. Lewellen, and S. F. Parker, On the vorticity dynamics of
a turbulent jet in a crossflow, J. Fluid Mech., 168, 393-413,
1986.
Trivett, D. A., and A. J. Williams III, Effluent from diffuse hydrothermal
venting, 2, Measurements of plumes from diffuse hydrothermal vents at the southern
Juan de Fuca Ridge, J. Geophys. Res., 99, 18,417-18,432, 1994.
Turner, J. S., A comparison between buoyant vortex rings and vortex pairs,
J. Fluid Mech., 7, 419-432, 1960.
Turner, J. S., Buoyancy Effects in Fluids, 367 pp., Cambridge Univ.
Press, New York, 1973.
Weil, J., Plume rise, in Lectures on Air Pollution Modelling, edited
by A. Venkatram and J. C. Wyngaard, pp. 119-166, Am. Meteorol. Soc., Boston,
Mass., 1988.
Wu, J. M., A. D. Vakilli, and F. N. Yu, Investigations of the interacting flow
of nonsymmetric jets in a crossflow, AIAA J., 26, 940-947, 1988.
Wyngaard, J., The potential and limitations of direct and large-eddy simulations,
Comment 3, in Whither Turbulence? Turbulence at the Crossroads, edited
by J. L. Lumley, pp. 369-373, Springer-Verlag, New York, 1990.
Zhang, X., and A. F. Ghoniem, A computational model for the rise and dispersion
of wind-blown, buoyancy-driven plumes, II, Linearly stratified atmosphere, Atmos.
Environ., 28, 3005-3018, 1994.
Return to Abstract
PMEL Outstanding Papers
PMEL Publications Search
PMEL Homepage
 . The model is used to study effects
of rotation and indicate differences in plumes with respect to variation of
subgrid-scale turbulence intensity and cross-flow strength. Counterrotating
vorticity (
. The model is used to study effects
of rotation and indicate differences in plumes with respect to variation of
subgrid-scale turbulence intensity and cross-flow strength. Counterrotating
vorticity ( ) couplets in all three coordinate
directions develop in the lower plume stem at startup and follow the plume to
the level of neutral buoyancy; for a nonrotational case (
) couplets in all three coordinate
directions develop in the lower plume stem at startup and follow the plume to
the level of neutral buoyancy; for a nonrotational case ( = 0),
= 0),  patterns resemble those previously found
for jets injected into homogenous cross flow. Ambient fluid entrainment into
the convecting column is primarily from the upstream side, but deflection of
background flow around both sides of the rising column is the root of the relative
vorticity (
patterns resemble those previously found
for jets injected into homogenous cross flow. Ambient fluid entrainment into
the convecting column is primarily from the upstream side, but deflection of
background flow around both sides of the rising column is the root of the relative
vorticity ( z) couplet in the
lower plume. Turbulence intensity within the buoyant region of the plume and/or
globally controls smoothness and temporal variability of distal nonbuoyant plume
distributions, allowing or preventing oscillations of potential temperature,
z) couplet in the
lower plume. Turbulence intensity within the buoyant region of the plume and/or
globally controls smoothness and temporal variability of distal nonbuoyant plume
distributions, allowing or preventing oscillations of potential temperature,
 , for example, at background buoyancy frequency,
N. Over the range of turbulent mixing studied, rise height of plumes
did not change appreciably, but breadth of plumes, counterintuitively, increased
for decreasing turbulent mixing strength. Increasing cross-flow strength, U
, for example, at background buoyancy frequency,
N. Over the range of turbulent mixing studied, rise height of plumes
did not change appreciably, but breadth of plumes, counterintuitively, increased
for decreasing turbulent mixing strength. Increasing cross-flow strength, U ,
bends model plumes such that rise height
,
bends model plumes such that rise height 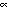 U
U -0.4.
For the two largest values of cross flow, for which R, the ratio of maximum
vertical velocity to U
-0.4.
For the two largest values of cross flow, for which R, the ratio of maximum
vertical velocity to U , took
values of 2.8 and 1.0, plumes showed evidence of bifurcation.
, took
values of 2.8 and 1.0, plumes showed evidence of bifurcation. 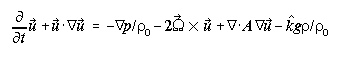
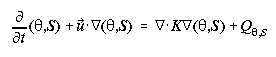
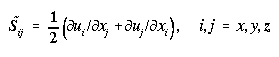
 is density;
is density;  ) is a reference density; g
(9.81 m
) is a reference density; g
(9.81 m s
s P
P .
Without point source heating, the steady background velocity profile uBKG
= (uBKG, vBKG) results from an Ekman horizontal
force balance (equation (1)):
.
Without point source heating, the steady background velocity profile uBKG
= (uBKG, vBKG) results from an Ekman horizontal
force balance (equation (1)): 
 .
Profile shapes and magnitudes nominally represent conditions in the lowest 300
m of water column above the seafloor spreading center of the Juan de Fuca Ridge,
northeast Pacific. The AZ profile controlling the boundary
layer thickness is hypothetical, but the shape and magnitude are generally consistent
with AZ values deduced from benthic ocean measurements at
other sites.
.
Profile shapes and magnitudes nominally represent conditions in the lowest 300
m of water column above the seafloor spreading center of the Juan de Fuca Ridge,
northeast Pacific. The AZ profile controlling the boundary
layer thickness is hypothetical, but the shape and magnitude are generally consistent
with AZ values deduced from benthic ocean measurements at
other sites. 
 (x,y,z)
caused by heating. In actual practice, hydrostatic terms are first subtracted
from (1), with the consequence that in resulting equations, p represents
the sum of P
(x,y,z)
caused by heating. In actual practice, hydrostatic terms are first subtracted
from (1), with the consequence that in resulting equations, p represents
the sum of P
 0
0  (
(

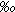 , 1.8925
× 10
, 1.8925
× 10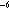 m
m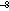 °C m
°C m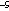

 ,
Ny, Nz, and N
,
Ny, Nz, and N were 128, 64, 32, and 2000 (or 5760).
were 128, 64, 32, and 2000 (or 5760). 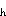 , was
set at 1.3 × 10
, was
set at 1.3 × 10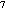 J s
J s Q
Q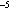 °C
°C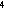 s
s would, over a source area of 10 × 10 m, give a Q
would, over a source area of 10 × 10 m, give a Q ,
,
 ,
,
 )
was (0, 0, 5.14 × 10
)
was (0, 0, 5.14 × 10 )1/4
)1/4
 and lROT
help organize experimental, observational, and occasionally numerical
and lROT
help organize experimental, observational, and occasionally numerical  )
N
)
N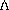 = 0.15 was
applied each time step to control temporal mode splitting. Integrations involved
solving a 3-D Poisson equation for p
= 0.15 was
applied each time step to control temporal mode splitting. Integrations involved
solving a 3-D Poisson equation for p 

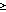 1.5 cm/s) that neither
upstream nor significant cross-stem plume growth occurs. Flows in and around
the stem and plume cap region, which result from the superposition of background
and convective flows, are also much different than flows expected in and around
convective plumes rising into a quiescent background environment
1.5 cm/s) that neither
upstream nor significant cross-stem plume growth occurs. Flows in and around
the stem and plume cap region, which result from the superposition of background
and convective flows, are also much different than flows expected in and around
convective plumes rising into a quiescent background environment 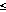 0.01 °C in field data is difficult, a single
hydrothermal source of the given size in this stratification environment ought
to be difficult to detect thermally beyond several hundred meters from the vent
source.
0.01 °C in field data is difficult, a single
hydrothermal source of the given size in this stratification environment ought
to be difficult to detect thermally beyond several hundred meters from the vent
source. 
 0 (
0 (


