U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
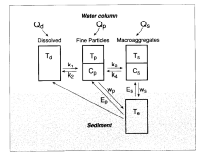
The model addresses the physical dispersion of hydrothermal Mn in dissolved, fine particulate and macroaggregate forms as well as the exchanges of Mn between those reservoirs (Figure 2). Dissolved Mn is sorped to and remobilized from fine particles and fine particles are physically scavenged by and result from the disaggregation of or release from macroaggregates, particles of relatively large size and settling velocity [e.g., Fowler and Knauer, 1986; Alldredge and Silver, 1988]. Macroaggregate Mn is that Mn which has been adsorbed onto or incorporated into macroaggregates. Steady, one-dimensional models of tracer transport and exchange having some of the features of the present model have been used previously by Nozaki et al. [1987], Clegg and Whitfield [1990], Murname et al. [1990] and Lavelle et al. [1991] to examine vertical distributions of Th. Unlike the Th models, the Mn model here is two dimensional and incorporates both an upward benthic flux of dissolved Mn and the resuspension of particles bearing Mn, each occurring at the seafloor.
Figure 2. Diagram of the Mn reservoirs and exchange pathways incorporated in the scavenging model. The physical processes of advection and diffusion are not represented.
The rates of exchange between Mn reservoirs are determined by the rate coefficients,
k through k
through k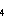 .
These are bulk exchange coefficients that represent the net effect of many underlying
biogeochemical processes [e.g.,
Nyffeler et al., 1984; Honeyman
et al., 1988]. Direct exchange between dissolved and macroaggregate
Mn reservoirs is possible but it is likely of secondary importance; the results
of Cowen
and Li [1991] suggest that small capsuled bacteria dominate the dMn
scavenging process. Concentrations of Mn in dissolved, fine particulate, and
macroaggregate forms are designated T
.
These are bulk exchange coefficients that represent the net effect of many underlying
biogeochemical processes [e.g.,
Nyffeler et al., 1984; Honeyman
et al., 1988]. Direct exchange between dissolved and macroaggregate
Mn reservoirs is possible but it is likely of secondary importance; the results
of Cowen
and Li [1991] suggest that small capsuled bacteria dominate the dMn
scavenging process. Concentrations of Mn in dissolved, fine particulate, and
macroaggregate forms are designated T ,
T
,
T , and T
, and T .
The letter T denotes tracer concentration, and s is used to denote
"marine snow," a term sometimes used to describe marine macroaggregates
[e.g.,
Silver and Alldredge, 1981]. The fine particles and macroaggregates
settle with velocities w
.
The letter T denotes tracer concentration, and s is used to denote
"marine snow," a term sometimes used to describe marine macroaggregates
[e.g.,
Silver and Alldredge, 1981]. The fine particles and macroaggregates
settle with velocities w and w
and w . Q
. Q represents the rate of discharge of dissolved Mn from the vents.
represents the rate of discharge of dissolved Mn from the vents.
The physical transport of Mn is determined by the processes of settling, advection, and turbulent diffusion. These aspects of the model were kept simple in order to focus on the effects of exchange processes (Figure 2). Consequently, steady off-axis advection, constant diffusivity both in space and time, and a source and resulting Mn distributions having no along-ridge dependence were all assumed. This last assumption permits the plumes to be treated in two dimensions, the off-axis and vertical. This implies that the entire ridge crest supplies Mn to the water column, a view of the hydrothermal system that may be realistic in a long-term sense since tectonic and magmatic activity which force hydrothermal circulation occur over the entire ridge.
Statements of mass conservation, including exchange terms, for each of the three forms of Mn are
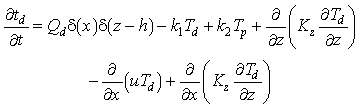 (1)
(1)
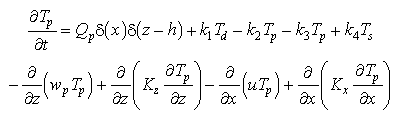 (2)
(2)
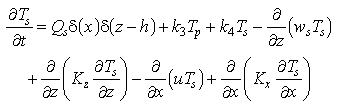 (3)
(3)
where t is time, x and z are the horizontal and vertical
axes, and  is the Dirac delta function [e.g.,
Morse and Feshbach, 1953]. The delta function indicates that Q
is the Dirac delta function [e.g.,
Morse and Feshbach, 1953]. The delta function indicates that Q ,
Q
,
Q , and Q
, and Q are steady point sources located at x = 0 and z = h. The
horizontal advection velocity is u and horizontal and vertical turbulent
diffusivities are K
are steady point sources located at x = 0 and z = h. The
horizontal advection velocity is u and horizontal and vertical turbulent
diffusivities are K and
K
and
K , respectively. The exchange
terms are based on those of Nozaki
et al. [1987]; they are independent of particle concentration [Honeyman
et al., 1988] because of the reasonably small range of particle concentrations
encountered in this particular problem.
, respectively. The exchange
terms are based on those of Nozaki
et al. [1987]; they are independent of particle concentration [Honeyman
et al., 1988] because of the reasonably small range of particle concentrations
encountered in this particular problem.
Equations (1)-(3) have been solved in a region of constant depth extending from the seafloor to 500 m above. The height was chosen to accommodate a source point centered at 240 m; typical nonbuoyant plumes near the ridge are centered vertically several hundred meters from the seafloor [e.g., Baker and Massoth, 1987]. In the steady state examples to follow, Mn at the source was spread vertically over 75 m, a choice guided by observations. The horizontal extent of the solution region, 330 km westward and 80 km eastward, was chosen to encompass much of the Mn deposition area. The off-axis orientation of the observational transects define the direction of the x axis. The advection velocity, u, consequently represents the off-axis component of mean flow.
The solution is dependent on values given model parameters, examined in detail below, and on model boundary conditions. As do the model equations, the boundary conditions apply only to the hydrothermal component of the Mn field. Background concentrations of Mn are not addressed by the model nor have background Mn concentrations been added to model results.
At the upstream and downstream ends of the solution domain, for all z
and for all three water column phases of Mn, a zero concentration gradient condition,
 T
T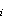 /dx
= 0 (for i = d, p, s), was imposed. This is a numerically
tolerant condition, one that allows advective transport of Mn through the upstream
and downstream boundaries without having to prescribe the magnitude of Mn concentration
or flux there.
/dx
= 0 (for i = d, p, s), was imposed. This is a numerically
tolerant condition, one that allows advective transport of Mn through the upstream
and downstream boundaries without having to prescribe the magnitude of Mn concentration
or flux there.
At the upper boundary (z = 500 m), for all x and all three Mn phases, a zero vertical flux condition was prescribed:
![]() (4)
(4)
Dissolved Mn has no settling velocity, of course, so w (equation (4)) is zero.
(equation (4)) is zero.
Seafloor boundary conditions must be drawn with care. Consideration must be given to the possibility of remobilization of Mn in the sediment column and subsequent diffusion of dMn back into the water column. Such a "benthic flux" has been argued even for "oxic" sediments at MANOP Site M [Kalhorn and Emerson, 1984; Heggie et al., 1986]. Oxidation of organic matter in the top centimeter of the sediment column is said to result in dMn gradients in pore waters that favor upward diffusion of dMn at the sediment-water interface.
This idea is consistent with the longer held view, based on more coarsely resolved profiles, that Mn is remobilized deeper in the core, diffuses upward, and is reoxidized in the surficial layers of sediments. Cores taken in the vicinity of the JDFR [Jones and Murray, 1985; G. Massoth, unpublished data, 1987] reveal little dMn in the upper few centimeters of the cores compared to that lower in the Mn reducing layer. Remobilization and upward diffusion result in surface sediments enriched in pMn far above that which might be expected of particles settling to the seafloor.
Near-bottom water column gradients of dMn are observed [e.g., Cowen et al., 1986] suggesting diffusion of dMn out of the sediments. The bottom boundary condition for dMn was consequently chosen to permit an upward benthic flux. Diffusive flux of dMn was made proportional to the settling flux of Mn:
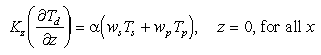 (5)
(5)
Fixed fraction of the settled Mn is diffused back into the water column as
dMn. The proportionality constant,  , can take
a value between 0 and 1. A value of 1 would lead to no Mn accumulation in the
sediments and a value of 0 would indicate complete retention of settled Mn in
the sediment column and no dMn gradients in the near-bottom water column. An
intermediate value needs to be chosen to be consistent with long-term Mn accumulation
rates and with dMn water column profiles. While not well defined by measurements,
an
, can take
a value between 0 and 1. A value of 1 would lead to no Mn accumulation in the
sediments and a value of 0 would indicate complete retention of settled Mn in
the sediment column and no dMn gradients in the near-bottom water column. An
intermediate value needs to be chosen to be consistent with long-term Mn accumulation
rates and with dMn water column profiles. While not well defined by measurements,
an  value of 0.1 appears to be consistent with
both for the region of study.
value of 0.1 appears to be consistent with
both for the region of study.
The boundary conditions of Mn flux in particulate phases are drawn in analogy to the boundary condition of particle flux at the seafloor:
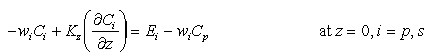 (6)
(6)
where E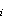 is the sediment
erosion rate [e.g.,
Parthenaides, 1972; Lavelle
et al., 1984], and w
is the sediment
erosion rate [e.g.,
Parthenaides, 1972; Lavelle
et al., 1984], and w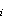 and C
and C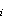 are the settling
velocity and particle concentration for settling velocity class i. Total
particle flux at the sediment water interface is thus the difference between
an upward erosive flux and a downward settling flux.
are the settling
velocity and particle concentration for settling velocity class i. Total
particle flux at the sediment water interface is thus the difference between
an upward erosive flux and a downward settling flux.
In analogy, the bottom boundary conditions on fine particulate and macroaggregate Mn were taken to be
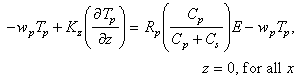 (7)
(7)
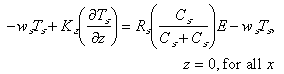 (8)
(8)
The erosional fluxes have been partitioned so that rates are proportional to
the particle concentration of each particle class at the seafloor. The erosion
terms are also proportional to R and R
and R , the mass fractions
of Mn on fine and macroaggregate particles. In the water column, these fractions
are equal to the functions T
, the mass fractions
of Mn on fine and macroaggregate particles. In the water column, these fractions
are equal to the functions T /C
/C and T
and T /C
/C ,
respectively, evaluated at a point of interest. At the sediment-water interface
R
,
respectively, evaluated at a point of interest. At the sediment-water interface
R and R
and R may exceed lower water column values because diagenetic processes can enrich
sedimented particles with Mn. For the purposes of these calculations, however,
R
may exceed lower water column values because diagenetic processes can enrich
sedimented particles with Mn. For the purposes of these calculations, however,
R = T
= T /C
/C and R
and R = T
= T /C
/C are based on values of component concentrations just above the seafloor. Under
these assumptions, equations (7) and (8) result in
are based on values of component concentrations just above the seafloor. Under
these assumptions, equations (7) and (8) result in
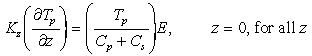 (9)
(9)
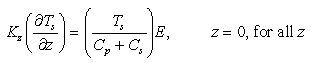 (10)
(10)
Manganese fluxes at the seafloor (equations (5), (7), and (8)), when summed,
yield the net Mn accumulation rate, D in the sediments:
in the sediments:
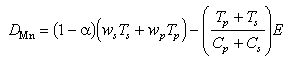 (11)
(11)
This net Mn accumulation rate is seen to be the sum of the settling flux in both particulate phases less the sum of dissolved benthic and particle erosional fluxes.
Specifying the boundary conditions (equations (4), (5), (9), and (10)) allows
equations (1)-(3) to be integrated. Steady state and time dependent solutions
were obtained numerically; the steady solution was achieved by integrating in
time until no further changes in variable fields occurred. Equations (1)-(3)
were center differenced to second-order accuracy in both space dimensions and
implicitly forward differenced in time. The T values were evaluated on grids staggered with respect to the u and K
values were evaluated on grids staggered with respect to the u and K grids. Final grid intervals were 5000 m in the x direction and 25 m and
6.25 m in the z direction for steady and time dependent problems, respectively.
K
grids. Final grid intervals were 5000 m in the x direction and 25 m and
6.25 m in the z direction for steady and time dependent problems, respectively.
K was reduced to its final
value (Table 2) during approach to steady state. Plume thicknesses were sensitive
to the value of K
was reduced to its final
value (Table 2) during approach to steady state. Plume thicknesses were sensitive
to the value of K (0.8
versus 2.0 cm
(0.8
versus 2.0 cm /s). For the time dependent solution,
the vertical advection term was upstream differenced and the time step judiciously
chosen (dt =
/s). For the time dependent solution,
the vertical advection term was upstream differenced and the time step judiciously
chosen (dt =  z/w
z/w )
to curtail unwanted numerical diffusion.
)
to curtail unwanted numerical diffusion.
The source strength, Q ,
was adjusted so that the dMn and pMn would concurrently have magnitudes comparable
to those observed in the transects (Figures 1a-1b
); Q
,
was adjusted so that the dMn and pMn would concurrently have magnitudes comparable
to those observed in the transects (Figures 1a-1b
); Q and Q
and Q are both zero for hydrothermal Mn. The horizontal advection velocity, u,
and macroaggregate scavenging rate, k
are both zero for hydrothermal Mn. The horizontal advection velocity, u,
and macroaggregate scavenging rate, k ,
were adjusted so that measured and modeled distributions of Mn accumulating
in sediments would be similar.
,
were adjusted so that measured and modeled distributions of Mn accumulating
in sediments would be similar.
Return to previous section or go to next section