
U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
A two-stage scavenging model is used to describe the transport of hydrothermal Mn to the sediments adjacent to ridge crests. Dissolved Mn is hypothesized to be scavenged by slowly settling metal-depositing capsuled bacteria which, in turn, are incorporated into rapidly settling macroaggregates. Upon reaching the seafloor, the Mn is subject to resuspension in particulate form and to remobilization within the sediment column and release back into the water column as dissolved Mn. Measured Mn distributions in the vicinity of the southern Juan de Fuca Ridge and estimated values of process rate constants are used to limit the range of possible model outcomes. The results present a picture of water column distributions and fluxes of dissolved, fine particulate, and large-particle associated Mn in a plume advecting off axis. The model and best available parameter values suggest that more than 80% of the hydrothermal Mn is deposited within several hundred kilometers of the ridge crest, though dissolved Mn concentrations beyond that distance exceed background levels by many times. The residence time of hydrothermal Mn in the water column is of the order of several years. An off-axis component of advection of the order of 0.1-0.3 cm/s is needed to make similar the model and measured distributions of Mn depositing in the sediments.
Though it is well documented that hydrothermal Mn finds its way into sediments at relatively short distances from active ridge crests [e.g., Bostrom and Peterson, 1969; Dymond, 1981], the process by which this apparent rapid deposition occurs has been rarely studied [Lyle et al., 1986]. One step in the deposition process appears to involve capsuled bacteria. Cowen et al. [1986] documented the importance of metal-depositing capsuled bacteria in the uptake of dissolved Mn in hydrothermal plumes. They found that a large fraction of the Mn in the plume could be borne on the extracellular capsules found on some bacteria. Still, the uptake of Mn by capsuled bacteria cannot provide the whole answer because capsuled bacteria are too small (1-2 µm) to settle rapidly. A second step in the transport process is needed to accelerate the transport of these particles to the seafloor. That step, we propose, involves macroaggregates, large rapidly settling particles [e.g., Fowler and Knauer, 1986; Alldredge and Silver, 1988]. Large particles have been recognized for some time to dominate the vertical flux of particles in the ocean [e.g., McCave, 1975], and they have been implicated in the vertical transport of fine particles and particle-borne chemical constituents [e.g., Bishop et al., 1977; Honjo, 1980; Bacon et al., 1985; Fowler and Knauer, 1986; Nozaki et al., 1987]. Deep ocean transit of material from surface to seafloor can occur in the matter of weeks as a result [e.g., Deuser et al., 1981]. Consequently, it seems reasonable to suggest that macroaggregates scavenge Mn-bearing capsuled bacteria from hydrothermal plumes and deposit them on the seafloor. In this paper a model of the deposition process for hydrothermal Mn is developed that incorporates this double scavenging scheme. The consequences of the model for Mn water column distributions, fluxes, and deposition patterns are explored, and results are compared with Mn distributions measured on transects running normal to the southern Juan de Fuca Ridge at and below hydrothermal plume depth.
Observations of hydrothermally derived Mn in the water column and in sediments near ridge crests are numerous [see Rona, 1987]. Mn plumes extending many kilometers from ridge crests have been observed in the region of the East Pacific Rise [e.g., Klinkhammer and Hudson, 1986] and on the Juan de Fuca Ridge [e.g., Massoth et al., 1984; Cowen et al., 1986]. Plume dMn measured at high spatial resolution over the axial valley of the Juan de Fuca Ridge have recently been reported by Coale et al. [1991].
Off-axis distributions of dissolved (dMn) and particulate (pMn) manganese away from the southern Juan de Fuca Ridge (JDFR) determined from water samples acquired in 1985 and 1986 are shown in Figures 1a and 1b. Here dMn is defined operationally and refers to Mn passing through a 0.2-µm filter; Mn in colloidal form [e.g., Honeyman and Santschi, 1989] is included in this fraction. Particulate Mn is all Mn, as determined by X ray spectrometry [e.g., Feely et al., 1991], associated with particles retained by a 0.4-µm filter; this particulate fraction is expected to be composed primarily of fine, slowly settling particles [McCave, 1975]. Samples were taken on a transect running westward and normal to the Cleft Segment of the JDFR at Vent 3 [Baker and Massoth, 1987] to a distance of 308 km (Table 1). Sample bottles were tripped at the depth of an isopycnal surface, as determined in real time by conductivity-temperature-depth measurements, corresponding to the density over the ridge at midplume depth.
| Station | Distance, km | Depth, m | dMn, nmol/L | pMn, nmol/L |
|---|---|---|---|---|
| 1985 | ||||
| On-axis mean | 0.0 | 2071 | 54.3 | 1.43 |
| On-axis minima | 0.0 | 2071 | 43.0 | 1.21 |
| On-axis maxima | 0.0 | 2071 | 77.2 | 1.65 |
| P-4/8 | 4.5 | 2057 | 47.6 | 1.54 |
| Tow P-5/3 | 5.3 | 2084 | 73.3 | 1.35 |
| Tow P-5/4 | 6.1 | 2125 | 18.0 | 1.92 |
| Tow P-5/5 | 6.9 | 2112 | 15.9 | 1.76 |
| Tow P-5/6 | 9.5 | 2154 | 5.2 | 1.56 |
| P-7/9 | 18.4 | 2129 | 3.7 | 2.15 |
| P-13/12 | 43.0 | 2127 | 1.6 | 1.45 |
| P-9/14 | 72.0 | 2102 | 1.5 | 0.92 |
| P-12/14 | 100.0 | 2030 | 2.2 | 2.06 |
| P-10/14 | 150.0 | 2154 | 1.6 | 1.76 |
| P-11/13 | 308.0 | 2125 | 0.6 | 0.38 |
| 1986 | ||||
| SC-12/7 | 5.0 | 2075 | 40.7 | 0.88 |
| SC-13/3 | 15.0 | 2073 | 1.5 | 01.41 |
| SC-14/16 | 25.0 | 2079 | 1.5 | 1.69 |
| SC-15/7 | 50.0 | 2075 | 1.3 | 1.28 |
| SC-16/1 | 100.0 | 2075 | 1.5 | 1.25 |
| SC-17/7 | 150.0 | 2074 | 1.3 | 0.34 |
| Sample depths and distances from the ridge are indicated. Samples were taken along an isopycnal surface corresponding to the density over the ridge at plume depth. | ||||
Figure 1. (a) Dissolved and (b) total particulate Mn as a function of distance normal to the Cleft segment of the JDFR ridge as measured (Table 1) in 1985 (solid curve) and 1986 (dashed curve). (c) Total particulate Mn as weight percent in surficial sediments (Table 2).
Concentrations of dMn near the ridge, 43-77 nmol/L (Table 1), are many times
those of deep ocean background values in the North Pacific. Background dMn values
range from 0.2-0.5 nmol/L based on deep (>2000 m) samples at stations away
from continental margins taken by Martin
and Knauer [1982, 1985]
and Landing
and Bruland [1987]. For pMn, reported background values range from 0.07-0.3
nmol/L, based on the same data sets plus measurements by Feely
et al. [1992] at 50°8 N and 140°20
N and 140°20 W.
On our off-axis transects (Figure 1b),
pMn values exceed background values by a factor of 6 or more over the first
150 km away from the ridge (Table 1).
W.
On our off-axis transects (Figure 1b),
pMn values exceed background values by a factor of 6 or more over the first
150 km away from the ridge (Table 1).
Both transects (Figures 1a and 1b) show Mn declining off axis, but dMn concentrations change more rapidly. At a distance of 43 km, dMn concentrations are only 1.6 nmol/L, a factor of 30 lower than the on-axis mean value. The pMn concentrations show evidence of having an off-axis maximum, a feature consistent with the pMn data of Feely et al. [1992]. While some differences in 1985 and 1986 data sets exist, the consistency of the basic patterns between years might suggest some stability in the discharge and dispersion processes. It would be incorrect, however, to assume that any of these transects represent data obtained along the centerline of an ideally shaped plume. Flow direction and speed are too variable [Cannon et al., 1991]. The transects more likely represent a sampling of recent and relict plume effluent, the boundaries of which are difficult to distinguish.
Water column Mn data (Figures 1a and 1b) likely reflect the results of several years of hydrothermal discharge as well as the effects of horizontal and vertical dispersion. The Mn in sediments flanking ridge crests, on the other hand, record the history of hydrothermal discharge and dispersion over much longer periods of time. Diagenetic processes must be added to the list of factors that influence off-axis distributions of Mn in sediments.
Sediment cores along a second transect normal to the southern JDFR (locations in Table 2) provide data on surficial sediment pMn (Figure 1c). Thin scrapings of the surface layer from box cores were taken for Mn analysis. Slight variations in this methodology, when they occurred, are noted in Table 2. Samples were analyzed by X ray spectrometry, as for water column pMn samples [Feely et al., 1991]. Results are expressed as weight percent of Mn in sediments.
The resulting distribution of pMn in surficial sediments (Figure 1c) shows a maximum concentration of 4.7% by weight, occurring off axis at a distance of 22-28 km (Table 2). Nearer the ridge the weight fractions plunge toward 1%. A more gradual decline occurs at greater distances from the ridge, with the weight fraction reaching an average value of 0.38% at 308 km. In comparison, Jones and Murray [1985] found 3-4 % by weight of leachable Mn in the top 3 cm of sediment for cores located within ~30-40 km eastward of the northern JDFR. Data similar to that of Figure 1c to the east of the ridge (not shown) suggest some depositional symmetry about the ridge axis.
| Distance from | Water | pMn | ||||
|---|---|---|---|---|---|---|
| Station | Ridge, km | Latitude/Longitude | Depth, m | % by weight | ||
| BX6-1 | 2.5 | 44° | 41.9' | N | 2256 | 1.42 |
| 130° | 24.79' | W | ||||
| B-6 | 3.3 | 44° | 39.0' | N | 2293 | 1.13 |
| 130° | 25.5' | W | ||||
| B-3 | 5.0 | 44° | 42.37' | N | 2352 | 0.98 |
| 130° | 26.81' | W | ||||
| SB-2 | 5.0 | 44° | 42.37' | N | 2344 | 1.86* |
| 130° | 26.16' | W | ||||
| B-2 | 7.4 | 44° | 40.0' | N | 2500 | 0.78* |
| 130° | 27.9' | W | ||||
| B-5 | 7.4 | 44° | 40.2' | N | --- | 3.07 |
| 130° | 30.9' | W | ||||
| B-4 | 11.7 | 44° | 41.2' | N | 2615 | 1.91 |
| 130° | 30.9' | W | ||||
| SB-1 | 15.0 | 44° | 43.8' | N | 2610 | 1.32* |
| 130° | 34.0' | W | ||||
| KC-1 | 15.6 | 44° | 42.21' | N | 2635 | 1.14++ |
| 130° | 33.8' | W | ||||
| B-9 | 15.7 | 44° | 42.2' | N | 2610 | 1.30 |
| 130° | 34.1' | W | ||||
| B-8 | 22 | 44° | 44.18' | N | 2960 | 4.69 |
| 130° | 38.52' | W | ||||
| B-12 | 28.2 | 44° | 45.28' | N | 2850 | 4.66 |
| 130° | 43.49' | W | ||||
| KC-4 | 43 | 44° | 48.75' | N | 2970 | 4.40+ |
| 130° | 52.05' | W | ||||
| B-13 | 48.6 | 44° | 49.87' | N | 2860 | 2.61 |
| 130° | 56.22' | W | ||||
| KC-3 | 72 | 44° | 58.21' | N | 3414 | 3.11+ |
| 131° | 35.65' | W | ||||
| B-14 | 100.6 | 45° | 03.4' | N | 3400 | 1.98 |
| 131° | 35.1' | W | ||||
| KC-2 | 308 | 45° | 31.57' | N | 3904 | 0.12+ |
| 134° | 0.63' | W | ||||
| BX6-2 | 308 | 45° | 30.26' | N | 3904 | 0.65 |
| 133° | 59.53' | W | ||||
| KC = Kasten core, SB = Soutar box core. | ||||||
| * Interval sampled 0-0.5 cm. | ||||||
| + Interval sampled 0-1.0 cm. | ||||||
| ++ Sampled at 2.5 cm from surface. | ||||||
The off-axis maximum in pMn weight percent in sediments is a feature observed at the East Pacific Rise (EPR) as well [Lyle, 1976]. Those data do not highly resolve at what distance the off-axis maximum occurs, but it is within 125 km of the ridge crest. Like our data (Table 2, Figure 1c), the pMn in sediments at the EPR decrease with distance off axis beyond the maximum in exponentiallike fashion. Weight fractions of Mn in sediments are much higher in that region, however. Dymond [1981] indicates Mn concentrations in surficial sediments higher than 10% by weight. In both regions the weight fractions reflect the Mn depositional flux and the results of diagenetic remobilization of Mn, upward migration of dMn, and the rescavenging of dMn by particulates in the oxic surface layer of the sediment column.
The model addresses the physical dispersion of hydrothermal Mn in dissolved, fine particulate and macroaggregate forms as well as the exchanges of Mn between those reservoirs (Figure 2). Dissolved Mn is sorped to and remobilized from fine particles and fine particles are physically scavenged by and result from the disaggregation of or release from macroaggregates, particles of relatively large size and settling velocity [e.g., Fowler and Knauer, 1986; Alldredge and Silver, 1988]. Macroaggregate Mn is that Mn which has been adsorbed onto or incorporated into macroaggregates. Steady, one-dimensional models of tracer transport and exchange having some of the features of the present model have been used previously by Nozaki et al. [1987], Clegg and Whitfield [1990], Murname et al. [1990] and Lavelle et al. [1991] to examine vertical distributions of Th. Unlike the Th models, the Mn model here is two dimensional and incorporates both an upward benthic flux of dissolved Mn and the resuspension of particles bearing Mn, each occurring at the seafloor.
Figure 2. Diagram of the Mn reservoirs and exchange pathways incorporated in the scavenging model. The physical processes of advection and diffusion are not represented.
The rates of exchange between Mn reservoirs are determined by the rate coefficients,
k through k
through k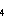 .
These are bulk exchange coefficients that represent the net effect of many underlying
biogeochemical processes [e.g.,
Nyffeler et al., 1984; Honeyman
et al., 1988]. Direct exchange between dissolved and macroaggregate
Mn reservoirs is possible but it is likely of secondary importance; the results
of Cowen
and Li [1991] suggest that small capsuled bacteria dominate the dMn
scavenging process. Concentrations of Mn in dissolved, fine particulate, and
macroaggregate forms are designated T
.
These are bulk exchange coefficients that represent the net effect of many underlying
biogeochemical processes [e.g.,
Nyffeler et al., 1984; Honeyman
et al., 1988]. Direct exchange between dissolved and macroaggregate
Mn reservoirs is possible but it is likely of secondary importance; the results
of Cowen
and Li [1991] suggest that small capsuled bacteria dominate the dMn
scavenging process. Concentrations of Mn in dissolved, fine particulate, and
macroaggregate forms are designated T ,
T
,
T , and T
, and T .
The letter T denotes tracer concentration, and s is used to denote
"marine snow," a term sometimes used to describe marine macroaggregates
[e.g.,
Silver and Alldredge, 1981]. The fine particles and macroaggregates
settle with velocities w
.
The letter T denotes tracer concentration, and s is used to denote
"marine snow," a term sometimes used to describe marine macroaggregates
[e.g.,
Silver and Alldredge, 1981]. The fine particles and macroaggregates
settle with velocities w and w
and w . Q
. Q represents the rate of discharge of dissolved Mn from the vents.
represents the rate of discharge of dissolved Mn from the vents.
The physical transport of Mn is determined by the processes of settling, advection, and turbulent diffusion. These aspects of the model were kept simple in order to focus on the effects of exchange processes (Figure 2). Consequently, steady off-axis advection, constant diffusivity both in space and time, and a source and resulting Mn distributions having no along-ridge dependence were all assumed. This last assumption permits the plumes to be treated in two dimensions, the off-axis and vertical. This implies that the entire ridge crest supplies Mn to the water column, a view of the hydrothermal system that may be realistic in a long-term sense since tectonic and magmatic activity which force hydrothermal circulation occur over the entire ridge.
Statements of mass conservation, including exchange terms, for each of the three forms of Mn are
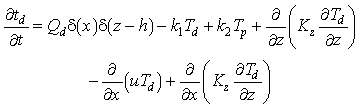 (1)
(1)
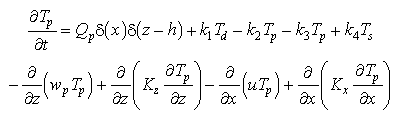 (2)
(2)
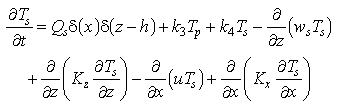 (3)
(3)
where t is time, x and z are the horizontal and vertical
axes, and  is the Dirac delta function [e.g.,
Morse and Feshbach, 1953]. The delta function indicates that Q
is the Dirac delta function [e.g.,
Morse and Feshbach, 1953]. The delta function indicates that Q ,
Q
,
Q , and Q
, and Q are steady point sources located at x = 0 and z = h. The
horizontal advection velocity is u and horizontal and vertical turbulent
diffusivities are K
are steady point sources located at x = 0 and z = h. The
horizontal advection velocity is u and horizontal and vertical turbulent
diffusivities are K and
K
and
K , respectively. The exchange
terms are based on those of Nozaki
et al. [1987]; they are independent of particle concentration [Honeyman
et al., 1988] because of the reasonably small range of particle concentrations
encountered in this particular problem.
, respectively. The exchange
terms are based on those of Nozaki
et al. [1987]; they are independent of particle concentration [Honeyman
et al., 1988] because of the reasonably small range of particle concentrations
encountered in this particular problem.
Equations (1)-(3) have been solved in a region of constant depth extending from the seafloor to 500 m above. The height was chosen to accommodate a source point centered at 240 m; typical nonbuoyant plumes near the ridge are centered vertically several hundred meters from the seafloor [e.g., Baker and Massoth, 1987]. In the steady state examples to follow, Mn at the source was spread vertically over 75 m, a choice guided by observations. The horizontal extent of the solution region, 330 km westward and 80 km eastward, was chosen to encompass much of the Mn deposition area. The off-axis orientation of the observational transects define the direction of the x axis. The advection velocity, u, consequently represents the off-axis component of mean flow.
The solution is dependent on values given model parameters, examined in detail below, and on model boundary conditions. As do the model equations, the boundary conditions apply only to the hydrothermal component of the Mn field. Background concentrations of Mn are not addressed by the model nor have background Mn concentrations been added to model results.
At the upstream and downstream ends of the solution domain, for all z and for
all three water column phases of Mn, a zero concentration gradient condition,  T
T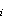 /dx
= 0 (for i = d, p, s), was imposed. This is a numerically
tolerant condition, one that allows advective transport of Mn through the upstream and
downstream boundaries without having to prescribe the magnitude of Mn concentration or
flux there.
/dx
= 0 (for i = d, p, s), was imposed. This is a numerically
tolerant condition, one that allows advective transport of Mn through the upstream and
downstream boundaries without having to prescribe the magnitude of Mn concentration or
flux there.
At the upper boundary (z = 500 m), for all x and all three Mn phases, a zero vertical flux condition was prescribed:
![]() (4)
(4)
Dissolved Mn has no settling velocity, of course, so w (equation (4)) is zero.
(equation (4)) is zero.
Seafloor boundary conditions must be drawn with care. Consideration must be given to the possibility of remobilization of Mn in the sediment column and subsequent diffusion of dMn back into the water column. Such a "benthic flux" has been argued even for "oxic" sediments at MANOP Site M [Kalhorn and Emerson, 1984; Heggie et al., 1986]. Oxidation of organic matter in the top centimeter of the sediment column is said to result in dMn gradients in pore waters that favor upward diffusion of dMn at the sediment-water interface.
This idea is consistent with the longer held view, based on more coarsely resolved profiles, that Mn is remobilized deeper in the core, diffuses upward, and is reoxidized in the surficial layers of sediments. Cores taken in the vicinity of the JDFR [Jones and Murray, 1985; G. Massoth, unpublished data, 1987] reveal little dMn in the upper few centimeters of the cores compared to that lower in the Mn reducing layer. Remobilization and upward diffusion result in surface sediments enriched in pMn far above that which might be expected of particles settling to the seafloor.
Near-bottom water column gradients of dMn are observed [e.g., Cowen et al., 1986] suggesting diffusion of dMn out of the sediments. The bottom boundary condition for dMn was consequently chosen to permit an upward benthic flux. Diffusive flux of dMn was made proportional to the settling flux of Mn:
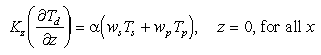 (5)
(5)
Fixed fraction of the settled Mn is diffused back into the water column as dMn. The
proportionality constant,  , can take a value between 0
and 1. A value of 1 would lead to no Mn accumulation in the sediments and a value of 0
would indicate complete retention of settled Mn in the sediment column and no dMn
gradients in the near-bottom water column. An intermediate value needs to be chosen to be
consistent with long-term Mn accumulation rates and with dMn water column profiles. While
not well defined by measurements, an
, can take a value between 0
and 1. A value of 1 would lead to no Mn accumulation in the sediments and a value of 0
would indicate complete retention of settled Mn in the sediment column and no dMn
gradients in the near-bottom water column. An intermediate value needs to be chosen to be
consistent with long-term Mn accumulation rates and with dMn water column profiles. While
not well defined by measurements, an  value of 0.1
appears to be consistent with both for the region of study.
value of 0.1
appears to be consistent with both for the region of study.
The boundary conditions of Mn flux in particulate phases are drawn in analogy to the boundary condition of particle flux at the seafloor:
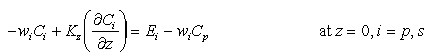 (6)
(6)
where E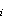 is the sediment
erosion rate [e.g.,
Parthenaides, 1972; Lavelle
et al., 1984], and w
is the sediment
erosion rate [e.g.,
Parthenaides, 1972; Lavelle
et al., 1984], and w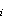 and C
and C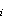 are the settling
velocity and particle concentration for settling velocity class i. Total
particle flux at the sediment water interface is thus the difference between
an upward erosive flux and a downward settling flux.
are the settling
velocity and particle concentration for settling velocity class i. Total
particle flux at the sediment water interface is thus the difference between
an upward erosive flux and a downward settling flux.
In analogy, the bottom boundary conditions on fine particulate and macroaggregate Mn were taken to be
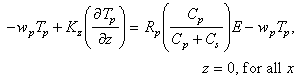 (7)
(7)
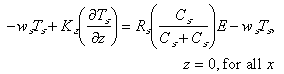 (8)
(8)
The erosional fluxes have been partitioned so that rates are proportional to the
particle concentration of each particle class at the seafloor. The erosion terms are also
proportional to R and R
and R , the mass fractions of Mn on fine and
macroaggregate particles. In the water column, these fractions are equal to the functions T
, the mass fractions of Mn on fine and
macroaggregate particles. In the water column, these fractions are equal to the functions T /C
/C and T
and T /C
/C , respectively, evaluated at a point of interest.
At the sediment-water interface R
, respectively, evaluated at a point of interest.
At the sediment-water interface R and
R
and
R may exceed lower water column
values because diagenetic processes can enrich sedimented particles with Mn. For the
purposes of these calculations, however, R
may exceed lower water column
values because diagenetic processes can enrich sedimented particles with Mn. For the
purposes of these calculations, however, R = T
= T /C
/C and R
and R = T
= T /C
/C are based on values of component concentrations
just above the seafloor. Under these assumptions, equations (7) and (8) result in
are based on values of component concentrations
just above the seafloor. Under these assumptions, equations (7) and (8) result in
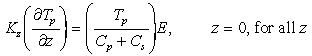 (9)
(9)
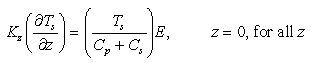 (10)
(10)
Manganese fluxes at the seafloor (equations (5), (7), and (8)), when summed, yield the
net Mn accumulation rate, D in the
sediments:
in the
sediments:
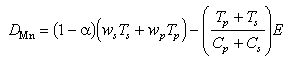 (11)
(11)
This net Mn accumulation rate is seen to be the sum of the settling flux in both particulate phases less the sum of dissolved benthic and particle erosional fluxes.
Specifying the boundary conditions (equations (4), (5), (9), and (10)) allows equations
(1)-(3) to be integrated. Steady state and time dependent solutions were obtained
numerically; the steady solution was achieved by integrating in time until no further
changes in variable fields occurred. Equations (1)-(3) were center differenced to
second-order accuracy in both space dimensions and implicitly forward differenced in time.
The T values were evaluated on grids
staggered with respect to the u and K
values were evaluated on grids
staggered with respect to the u and K grids. Final grid intervals were 5000 m in the x
direction and 25 m and 6.25 m in the z direction for steady and time dependent
problems, respectively. K
grids. Final grid intervals were 5000 m in the x
direction and 25 m and 6.25 m in the z direction for steady and time dependent
problems, respectively. K was reduced
to its final value (Table 2) during approach to steady state. Plume thicknesses were
sensitive to the value of K
was reduced
to its final value (Table 2) during approach to steady state. Plume thicknesses were
sensitive to the value of K (0.8
versus 2.0 cm
(0.8
versus 2.0 cm /s). For the time dependent solution, the
vertical advection term was upstream differenced and the time step judiciously chosen (dt
=
/s). For the time dependent solution, the
vertical advection term was upstream differenced and the time step judiciously chosen (dt
=  z/w
z/w ) to curtail unwanted numerical diffusion.
) to curtail unwanted numerical diffusion.
The source strength, Q , was
adjusted so that the dMn and pMn would concurrently have magnitudes comparable to those
observed in the transects (Figures 1a-1b ); Q
, was
adjusted so that the dMn and pMn would concurrently have magnitudes comparable to those
observed in the transects (Figures 1a-1b ); Q and Q
and Q are both zero for hydrothermal Mn. The horizontal advection
velocity, u, and macroaggregate scavenging rate, k
are both zero for hydrothermal Mn. The horizontal advection
velocity, u, and macroaggregate scavenging rate, k , were adjusted so that measured and modeled distributions of
Mn accumulating in sediments would be similar.
, were adjusted so that measured and modeled distributions of
Mn accumulating in sediments would be similar.
The sorption and remobilization rates, k ,
and k
,
and k , fix the exchange
of Mn between dissolved and fine particulate reservoirs. Cowen
and Li [1991] suggest that only a small fraction of the fine particles,
specifically the metal scavenging capsuled bacteria, are responsible for the
bulk of the dMn scavenging.
, fix the exchange
of Mn between dissolved and fine particulate reservoirs. Cowen
and Li [1991] suggest that only a small fraction of the fine particles,
specifically the metal scavenging capsuled bacteria, are responsible for the
bulk of the dMn scavenging.
The rate k was measured
by Cowen
et al. [1990] using the radioisotope
was measured
by Cowen
et al. [1990] using the radioisotope 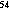 Mn
and water samples taken in the vicinity of the JDFR at ridge crest depth. Uptake
of dMn was seen to occur predominately with a time scale of the order of 1 year,
but faster time scales were also evident depending on the population of capsuled
bacteria. In fact, Cowen
and Li s [1991] data suggest that rate coefficients increase with plume
age and perhaps the scavenging efficiency of each capsule increases as well,
so k
Mn
and water samples taken in the vicinity of the JDFR at ridge crest depth. Uptake
of dMn was seen to occur predominately with a time scale of the order of 1 year,
but faster time scales were also evident depending on the population of capsuled
bacteria. In fact, Cowen
and Li s [1991] data suggest that rate coefficients increase with plume
age and perhaps the scavenging efficiency of each capsule increases as well,
so k may be other than a
constant. Such age and efficiency dependence cannot be encompassed at this stage
of model development. Instead k
may be other than a
constant. Such age and efficiency dependence cannot be encompassed at this stage
of model development. Instead k is here assumed to be constant in space and time (360 days)
is here assumed to be constant in space and time (360 days) .
.
No direct determinations of the remobilization rate of Mn from capsules, k , have yet been made. Consequently, Mn data from
deep ocean stations removed from hydrothermal influence are here used to suggest its
magnitude. If the similarity of the scavenging-remobilization process between hydrothermal
and nonhydrothermal regions can be assumed, and if dMn and pMn are nearly in exchange
equilibrium at stations well away from hydrothermal influence, the ratio pMn/dMn (~T
, have yet been made. Consequently, Mn data from
deep ocean stations removed from hydrothermal influence are here used to suggest its
magnitude. If the similarity of the scavenging-remobilization process between hydrothermal
and nonhydrothermal regions can be assumed, and if dMn and pMn are nearly in exchange
equilibrium at stations well away from hydrothermal influence, the ratio pMn/dMn (~T /T
/T ) at those distal stations may serve to approximate the ratio
k
) at those distal stations may serve to approximate the ratio
k /k
/k . T
. T differs from pMn in that pMn includes macroaggregate Mn, but macroaggregate Mn should have
little effect on the ratio k
differs from pMn in that pMn includes macroaggregate Mn, but macroaggregate Mn should have
little effect on the ratio k /k
/k because of the relatively low concentration of
macroaggregates compared to fine particles. Of course, strict equilibrium cannot be
achieved when particles are undergoing removal to the seafloor by settling, but
partitioning data presently provide the best available means of narrowing the range of
possible values for k
because of the relatively low concentration of
macroaggregates compared to fine particles. Of course, strict equilibrium cannot be
achieved when particles are undergoing removal to the seafloor by settling, but
partitioning data presently provide the best available means of narrowing the range of
possible values for k .
.
Only measurements taken at depths greater than 1500 m are considered here.
Landing
and Bruland [1987], for a station at 15°N and 160°W, present dMn and
pMn data that lead to a average value for k /k
/k of 0.33. Individual values ranged from 0.17 to 0.66, with the lowest and highest
values occurring at 3000 m and near the seafloor, respectively. For a station
"~2000 km west of central Mexico" and at 1500 m, Martin
and Knauer [1982, p. 1214] report dMn and pMn concentrations that lead
to a k
of 0.33. Individual values ranged from 0.17 to 0.66, with the lowest and highest
values occurring at 3000 m and near the seafloor, respectively. For a station
"~2000 km west of central Mexico" and at 1500 m, Martin
and Knauer [1982, p. 1214] report dMn and pMn concentrations that lead
to a k /k
/k average of 0.29. At 28°N and 155°W, Martin
and Knauer s [1985] data for 2000 m suggest k
average of 0.29. At 28°N and 155°W, Martin
and Knauer s [1985] data for 2000 m suggest k /k
/k = 0.13. Samples at 1500-1600 m depth near the JDFR show dMn ranging from 0.7
to 1.6 nmol/L and pMn ranging from 0.2 to 0.5 nmol/L [Cowen
et al., 1990; Cowen
and Li, 1991]. These dMn and pMn values are both slightly above the
background ranges that were inferred from data at more distant stations, as
earlier described, and they lead to k
= 0.13. Samples at 1500-1600 m depth near the JDFR show dMn ranging from 0.7
to 1.6 nmol/L and pMn ranging from 0.2 to 0.5 nmol/L [Cowen
et al., 1990; Cowen
and Li, 1991]. These dMn and pMn values are both slightly above the
background ranges that were inferred from data at more distant stations, as
earlier described, and they lead to k /k
/k ratios ranging from 0.2 to 0.57. Thus even at these depths on the JDFR there
may normally be some hydrothermal effect. Episodic influence of hydrothermal
activity at 1500 m is certain [Baker
et al., 1989]. In comparison, for points between 500 and 1000 m above
the bottom over the mid-Atlantic ridge, a depth interval which is presumed to
be out of hydrothermal influence, Klinkhammer
et al. [1985] found Mn concentrations that result in an average k
ratios ranging from 0.2 to 0.57. Thus even at these depths on the JDFR there
may normally be some hydrothermal effect. Episodic influence of hydrothermal
activity at 1500 m is certain [Baker
et al., 1989]. In comparison, for points between 500 and 1000 m above
the bottom over the mid-Atlantic ridge, a depth interval which is presumed to
be out of hydrothermal influence, Klinkhammer
et al. [1985] found Mn concentrations that result in an average k /k
/k ratio of 0.26. All these k
ratio of 0.26. All these k /k
/k estimates are based, of course, on the assumption that chemical exchange equilibrium
prevails.
estimates are based, of course, on the assumption that chemical exchange equilibrium
prevails.
Taken together, these estimates suggest that the time scale for remobilization of Mn
from fine particles is about 1/3 the length of the time scale for dMn scavenging. On the
other hand, if particles other than metal scavenging bacteria play an important role in Mn
scavenging in these background regions, the k /k
/k ratios
in hydrothermal regions may be somewhat different than 1/3. In the analysis to follow, we
will use separate values of 1/3 and 3 for k
ratios
in hydrothermal regions may be somewhat different than 1/3. In the analysis to follow, we
will use separate values of 1/3 and 3 for k /k
/k in
order to examine the model dependence over a range of remobilization rates. Since k
in
order to examine the model dependence over a range of remobilization rates. Since k is chosen to be (360 days)
is chosen to be (360 days) , k
, k then has values of (120 days)
then has values of (120 days) and (1080 days)
and (1080 days) , respectively, for the two stated values of the k
, respectively, for the two stated values of the k /k
/k ratio.
ratio.
Estimates for the rate of fine particle scavenging by macroaggregates, k ,
are just beginning to appear in the literature. Nozaki
et al. [1987] used two
,
are just beginning to appear in the literature. Nozaki
et al. [1987] used two 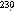 Th profiles
from the western Pacific to infer k
Th profiles
from the western Pacific to infer k values of (30 days)
values of (30 days) and (154 days)
and (154 days) ,
though Lavelle
et al. [1991] claim, by reanalyzing the same data, that k
,
though Lavelle
et al. [1991] claim, by reanalyzing the same data, that k for that data is more likely (320-370 days)
for that data is more likely (320-370 days) .
In a deep estuary with particle concentrations much higher than the deep ocean,
k
.
In a deep estuary with particle concentrations much higher than the deep ocean,
k has been estimated to
be (2-6 days)
has been estimated to
be (2-6 days) [Lavelle
et al., 1991].
[Lavelle
et al., 1991].
In the Panama Basin, Asper
[1987] measured size, number density, and settling velocity of macroaggregates,
all factors in determining the k scavenging rate. Consider a unit volume of water in which the number density
of macroaggregates is N. Let the macroaggregates have a common settling
velocity of w
scavenging rate. Consider a unit volume of water in which the number density
of macroaggregates is N. Let the macroaggregates have a common settling
velocity of w and a common
cross-sectional impact diameter of d. During any time interval dt,
each of N macroaggregates sweeps a volume of water equal to (
and a common
cross-sectional impact diameter of d. During any time interval dt,
each of N macroaggregates sweeps a volume of water equal to ( /4)d
/4)d w
w dt. If the mass
concentration of fine particles in the same unit volume of water is C,
and if the fine particles encountered by each macroaggregate are scavenged with
a retention efficiency
dt. If the mass
concentration of fine particles in the same unit volume of water is C,
and if the fine particles encountered by each macroaggregate are scavenged with
a retention efficiency  (0
(0 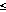

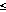 1), then
the rate of fine particle removal by macroaggregate scavenging would be
1), then
the rate of fine particle removal by macroaggregate scavenging would be
![]() (12)
(12)
The term in brackets represents the scavenging rate k .
The rate depends on d, N, and w
.
The rate depends on d, N, and w ,
which Asper
[1987] measured, and the scavenging efficiency
,
which Asper
[1987] measured, and the scavenging efficiency  .
.
Asper
[1987] found macroaggregate size classes with diameters 2 and 3.4 mm contributed
89 % of the large particle flux at his Panama Basin site. The smaller size class
(2 mm) settled at an average speed of 36 m/d and had number density of 1.4 particles
per liter. The larger size class (3.4 mm) settled at an average speed of 26
m/d and had a number density of 0.58 particles per liter. If  = 1, these data and equation (12) result in k
= 1, these data and equation (12) result in k values of (6 days)
values of (6 days) and (5 days)
and (5 days) ,
respectively. For smaller values of
,
respectively. For smaller values of  , k
, k is made smaller and the scavenging time scale T
is made smaller and the scavenging time scale T (
= 1/k
(
= 1/k ) is lengthened proportionately.
If
) is lengthened proportionately.
If  were 0.2, a k
were 0.2, a k value of approximately (30 days)
value of approximately (30 days) would result,
and if
would result,
and if  were -0.02, a value for k
were -0.02, a value for k closer to (360 days)
closer to (360 days) would result. This
uncertainty in assigning a value to
would result. This
uncertainty in assigning a value to  is exacerbated
by the likely site-to-site variability of the other factors determining k
is exacerbated
by the likely site-to-site variability of the other factors determining k .
In the absence of appropriate data, no certain value for k
.
In the absence of appropriate data, no certain value for k can be assigned for the JDFR region, but it does seem reasonable to assume that
T
can be assigned for the JDFR region, but it does seem reasonable to assume that
T has a time scale of weeks
to months. Here we have chosen to examine the consequences of k
has a time scale of weeks
to months. Here we have chosen to examine the consequences of k ranging from (20 days)
ranging from (20 days) to (180 days)
to (180 days) ,
using a k
,
using a k of (60 days)
of (60 days) around which to center the analysis.
around which to center the analysis.
The final exchange rate, k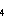 ,
determines the time scale for release of fine particles from macroaggregates.
The release process is not well defined, but k
,
determines the time scale for release of fine particles from macroaggregates.
The release process is not well defined, but k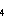 must include the effects of total or partial large-particle disaggregation or
other mechanisms of fine particle loss from macroaggregates. The Western Pacific
data of Nozaki
et al. [1987] suggest that an appropriate time scale, T
must include the effects of total or partial large-particle disaggregation or
other mechanisms of fine particle loss from macroaggregates. The Western Pacific
data of Nozaki
et al. [1987] suggest that an appropriate time scale, T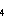 (
= 1/k
(
= 1/k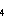 ), is ~6 days [Lavelle
et al., 1991]. Apparently, the scavenging of fine particles occurs
more slowly than does fine particle release. The T
), is ~6 days [Lavelle
et al., 1991]. Apparently, the scavenging of fine particles occurs
more slowly than does fine particle release. The T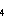 adopted here is 6 days. This time is long compared to the transit time from
a height of 240 m (model source height) to the seafloor if macroaggregates settle
at a speed as high as 100 m/d [e.g.,
Alldredge and Silver, 1988]. Consequently, in this model environment,
the release to the water column below plume depth of capsuled bacteria by macroaggregates
can occur, but the process is not favored.
adopted here is 6 days. This time is long compared to the transit time from
a height of 240 m (model source height) to the seafloor if macroaggregates settle
at a speed as high as 100 m/d [e.g.,
Alldredge and Silver, 1988]. Consequently, in this model environment,
the release to the water column below plume depth of capsuled bacteria by macroaggregates
can occur, but the process is not favored.
Observations of currents within the central ridge valley and adjacent regions of the southern JDFR show a spatially complicated and time variable pattern of flow [Cannon et al., 1991]. Tidal, inertial, and atmospherically induced 4-day oscillations dominate the spectra of currents. Mean currents from observations exceeding 6 months in duration for locations below 2100 m (~ ridge crest depth) range from 0.3 to 1.9 cm/s, but the directions are principally northward and southward along the ridge rather than off axis. Occasional divergent off-axis subtidal flow of duration exceeding several weeks is observed.
The evidence on longer term off-axis mean flow is more circumstantial. Reid s [1981] diagrams of phosphate and silica concentrations on an isopycnal surface at approximately 2600 m depth suggest westward mean flow near the JDFR. The patterns of Mn in sediments (Figure 1c), as they do on the EPR [Klinkhammer and Hudson, 1986], suggest long-term off-axis flow as well. Stommel s [1982] model of baroclinic flow caused by hydrothermal heat flux for the EPR suggests a westward mean flow with speeds of -0.2 cm/s. J. Lupton (personal communication, 1991) suggests that a helium plume extends to the southwest of the southern JDFR. Differences in these suggestions and the results of Cannon et al. [1991] may be related to the shorter averaging time and more limited spatial scales of the current meter observations.
The one-dimensional nature and off-axis orientation of the data confine our present analysis to the component of mean flow in the off-axis direction only. Should long-term mean flow actually be directed other than westward in the southern JDFR region, any suggestions of the magnitude of off-axis advection derived here must apply only to the ridge-normal component of that flow. The Mn sediment data and limitations on scavenging time scales restrict the range of possible current speeds allowed that component, however.
Vertical eddy diffusivity, K ,
is given a value of 8 × 10
,
is given a value of 8 × 10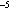 cm
cm /s,
though values range from 10
/s,
though values range from 10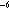 to 3-4 × 10
to 3-4 × 10 cm
cm /s in the deep ocean away from boundaries,
regions where velocity shears are low [e.g.,
Garrett, 1979; Gargett,
1984]. For our purpose, K
/s in the deep ocean away from boundaries,
regions where velocity shears are low [e.g.,
Garrett, 1979; Gargett,
1984]. For our purpose, K is taken to be vertically uniform. At the seafloor, values for K
is taken to be vertically uniform. At the seafloor, values for K 10 to 50 times those are more likely appropriate [e.g.,
Garrett, 1979], but the effects of increased benthic boundary layer
turbulence and bathymetry on Mn distributions are both left for later study.
Horizontal diffusivity, K
10 to 50 times those are more likely appropriate [e.g.,
Garrett, 1979], but the effects of increased benthic boundary layer
turbulence and bathymetry on Mn distributions are both left for later study.
Horizontal diffusivity, K ,
is given a value of 10 m
,
is given a value of 10 m /s [e.g.,
Okubo, 1971]. This diffusivity accounts for the effects on Mn distributions
of unresolved currents including tidal flow, and it permits some upstream presence
of Mn as indicated, for example, by observations of pMn across the width of
the axial valley.
/s [e.g.,
Okubo, 1971]. This diffusivity accounts for the effects on Mn distributions
of unresolved currents including tidal flow, and it permits some upstream presence
of Mn as indicated, for example, by observations of pMn across the width of
the axial valley.
The settling velocity of fine particles, w ,
is set to 0.1 m/d in these model realizations. This corresponds to the Stokes
settling speed of, for example, 1.9 µm diameter particles with specific gravity
2.6 or 3.2 µm particles with a specific gravity of 1.55. Particles in this size
range have been documented in hydrothermal plumes of the southern JDFR [Walker
and Baker, 1988]. Furthermore, Cowen
et al. [1986] note that capsuled bacteria from the plumes have diameters
of 1-2 µm. The settling velocity of macroaggregates, w
,
is set to 0.1 m/d in these model realizations. This corresponds to the Stokes
settling speed of, for example, 1.9 µm diameter particles with specific gravity
2.6 or 3.2 µm particles with a specific gravity of 1.55. Particles in this size
range have been documented in hydrothermal plumes of the southern JDFR [Walker
and Baker, 1988]. Furthermore, Cowen
et al. [1986] note that capsuled bacteria from the plumes have diameters
of 1-2 µm. The settling velocity of macroaggregates, w ,
is understandably very much larger. The location closest to the JDFR at which
macroaggregate settling speed has been inferred is some 1300 km to the west-northwest
at Ocean Station Papa [Honjo,
1985; Asper,
1986]. Those data suggest that w
,
is understandably very much larger. The location closest to the JDFR at which
macroaggregate settling speed has been inferred is some 1300 km to the west-northwest
at Ocean Station Papa [Honjo,
1985; Asper,
1986]. Those data suggest that w is as much as 175 m/d, but the temporal resolution of the data makes the confidence
interval for that estimate large. In other regions the settling speed of macroaggregates
are found to have considerable range [e.g.,
Alldredge and Silver, 1988; Alldredge
and Gotschalk, 1988], with 100 m/d being considered a typical value.
For purpose of our analysis, w
is as much as 175 m/d, but the temporal resolution of the data makes the confidence
interval for that estimate large. In other regions the settling speed of macroaggregates
are found to have considerable range [e.g.,
Alldredge and Silver, 1988; Alldredge
and Gotschalk, 1988], with 100 m/d being considered a typical value.
For purpose of our analysis, w is set to that value.
is set to that value.
Particulate concentrations prove useful in evaluating Mn mass fractions. Concentrations
out of the plume and away from the seafloor, the background concentration of
particles, average 15 µg/L [Cowen
et al., 1986; Cowen
et al., 1990]. Within the plume, concentrations are 2-3 times this
[Cowen
et al., 1986]. Only a small fraction of this particulate concentration
is due to macroaggregates. Macroaggregate concentration can be estimated from
settling flux rates and the macroaggregate settling velocity. The reason is
that large particles should comprise the bulk of the vertical flux [e.g.,
McCave, 1975], so the settling flux is nearly equal to w C
C . At the Endeavor segment
of the JDFR, Dymond
and Roth [1988] trapped particles over a period of nearly a year; for
sample points away from the effects of resuspension, those flux data average
1.6 g/cm
. At the Endeavor segment
of the JDFR, Dymond
and Roth [1988] trapped particles over a period of nearly a year; for
sample points away from the effects of resuspension, those flux data average
1.6 g/cm /kyr. Duncan
[1968] measured a sediment accumulation rate of 3 cm/kyr in a core west
of the JDFR. This rate is comparable to that of Dymond
and Roth [1988] assuming a sediment porosity of 0.8 and a sediment density
of 2.6 g/cm
/kyr. Duncan
[1968] measured a sediment accumulation rate of 3 cm/kyr in a core west
of the JDFR. This rate is comparable to that of Dymond
and Roth [1988] assuming a sediment porosity of 0.8 and a sediment density
of 2.6 g/cm . Dividing flux by w
. Dividing flux by w (100
m/d) leads to a C
(100
m/d) leads to a C value
of 0.44 µg/L. This is less than 1/30th the concentration of fine particles,
but this is only a crude estimate for C
value
of 0.44 µg/L. This is less than 1/30th the concentration of fine particles,
but this is only a crude estimate for C that awaits better definition by direct field measurement. Model concentrations
C
that awaits better definition by direct field measurement. Model concentrations
C and C
and C are taken to be spatially uniform.
are taken to be spatially uniform.
The rate of erosion of sediment, E, was given a magnitude of 1.7 × 10 g/m
g/m /d, a flux rate about 4% that of the settling
flux. This rate is comparable to fine sediment erosion rates in shallower environments
under conditions of low bed stress [Lavelle
et al., 1984]. E, along with vertical diffusivity and settling
velocity, determines gradients of T
/d, a flux rate about 4% that of the settling
flux. This rate is comparable to fine sediment erosion rates in shallower environments
under conditions of low bed stress [Lavelle
et al., 1984]. E, along with vertical diffusivity and settling
velocity, determines gradients of T and T
and T at the seafloor (equations
(9) and (10)).
at the seafloor (equations
(9) and (10)).
Distributions and fluxes of Mn in all three phases were calculated using the model equations and parameter values just described. Those results and their sensitivity to variations in parameter values away from central ones (Table 3) follow.
| Value | Parameter |
|---|---|
k = (360
days) = (360
days) |
sorption rate of Mn onto fine particles |
k = (120
days) = (120
days) |
remobilization rate of Mn from fine particles |
k = (60
days) = (60
days) |
scavenging rate of fine by large particles |
k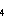 = (6
days) = (6
days) |
release rates of fine from large particles |
w = 0.1
m/d = 0.1
m/d |
fine particle settling velocity |
w = 100
m/d = 100
m/d |
large particle settling velocity |
C = 15
µg/L = 15
µg/L |
fine particulate concentration |
C = 0.44
µg/L = 0.44
µg/L |
macroaggregate concentration |
E = 1.7 × 10 g/m²/d
g/m²/d |
sediment erosion rate |
K = 0.8
cm²/s = 0.8
cm²/s |
vertical eddy diffusivity |
K = 10
m²/s = 10
m²/s |
horizontal eddy diffusivity |
| u = 0.2 cm/s | horizontal advection velocity westward |
| h = 240 m | Mn source height from seafloor |
Q = 4.8 × 10 g/m/s
g/m/s |
Mn source rate |
 = 0.1 = 0.1 |
benthic flux fraction |
Model transects of Mn in dissolved and fine particulate phases at plume height
(Figure 3, solid curve) have the general features
of the observations (Figure 1). Maximum values
of both model dissolved Mn (dMn = T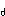 )
and total particulate Mn (pMn = T
)
and total particulate Mn (pMn = T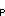 + T
+ T ) are within a factor
of 1.5 of the data, a result of the adjustment of the single parameter Q
) are within a factor
of 1.5 of the data, a result of the adjustment of the single parameter Q ,
the dMn source strength. Values for dMn peak on axis (x = 0, Figure
3), while those for pMn peak off axis; so do the data (Table 1). An off-axis
maximum is consistent with the pMn data of Feely
et al. [1992]. Both distributions decline sharply with distance off
axis, though dMn declines more slowly and pMn declines more quickly than the
observations suggest.
,
the dMn source strength. Values for dMn peak on axis (x = 0, Figure
3), while those for pMn peak off axis; so do the data (Table 1). An off-axis
maximum is consistent with the pMn data of Feely
et al. [1992]. Both distributions decline sharply with distance off
axis, though dMn declines more slowly and pMn declines more quickly than the
observations suggest.
Figure 3. Model results under parameter conditions of Table 3 showing off-axis
transects of (a) dissolved manganese (dMn = T ) and (b) total particulate manganese (pMn = T
) and (b) total particulate manganese (pMn = T + T
+ T ) at heights of (solid) 240 m and (dashed) 120 m. (c)
Model pMn flux (mg/cm
) at heights of (solid) 240 m and (dashed) 120 m. (c)
Model pMn flux (mg/cm /kyr) to the seafloor (solid curve)
and measured weight percent of Mn in surficial sediments (squares, Table 2).
/kyr) to the seafloor (solid curve)
and measured weight percent of Mn in surficial sediments (squares, Table 2).
The rate of decrease of dMn off axis depends on all model variables, but dMn
must be particularly sensitive to k and u, the advection speed. Accelerating the rate of conversion of dMn
to fine particulate form by enlarging k
and u, the advection speed. Accelerating the rate of conversion of dMn
to fine particulate form by enlarging k could make model and measured dMn distributions (Figures
1a and 3a) more alike. This
was not done because the value of k
could make model and measured dMn distributions (Figures
1a and 3a) more alike. This
was not done because the value of k would no longer as well match the field measurements [Cowen
and Li, 1991] and because Figure 1a
represents just two samples of water column distributions that are likely to
be highly variable about a long-term mean. Since the model is meant to address
longer-term mean conditions, matching Mn distributions in sediments was given
priority instead.
would no longer as well match the field measurements [Cowen
and Li, 1991] and because Figure 1a
represents just two samples of water column distributions that are likely to
be highly variable about a long-term mean. Since the model is meant to address
longer-term mean conditions, matching Mn distributions in sediments was given
priority instead.
Transects at a height of 120 m (dashed curve, Figure 3) have a very much different appearance. Distributions are broader and maxima are farther off axis. The comparison of these with those at 240 m show the importance to the interpretation of data of securing samples at a fixed plume horizon. All model transects show upstream concentrations caused by horizontal diffusion, the model surrogate for tidal dispersion. The off-axis pMn distributions and the location of the maxima reflect, first, the slow uptake of dMn by capsuled bacteria and, past the distribution maxima, the declining availability of dMn for scavenging.
A larger perspective on Mn cycling near the ridge is seen in the contoured
fields for each Mn phase (Figure 4). The dMn
concentrations of 2 nmol/L, several time background levels in the North Pacific
(0.2-0.5 nmol/L [e.g.,
Martin and Knauer, 1982, 1985;
Landing
and Bruland, 1987], extends more than 200 km downstream. Overall the
dMn plume is reminiscent of the  He plume measured
at the EPR [Lupton
and Craig, 1981], but dMn, unlike
He plume measured
at the EPR [Lupton
and Craig, 1981], but dMn, unlike  He,
is a nonconservative tracer and quantitative comparisons must be made cautiously.
Unlike the
He,
is a nonconservative tracer and quantitative comparisons must be made cautiously.
Unlike the  He plume, the dMn plume shows slightly
increasing concentrations at the seafloor, the result of remobilization of Mn
in sediments and diffusion back into the water column. This feature of the distribution
could be mistakenly interpreted as the consequence of a diffuse off-axis hydrothermal
source, when it is the result of Mn deposition patterns and Mn diagenesis in
the sediments. Diffuse off-axis hydrothermal sources of Mn cannot be ruled out,
however.
He plume, the dMn plume shows slightly
increasing concentrations at the seafloor, the result of remobilization of Mn
in sediments and diffusion back into the water column. This feature of the distribution
could be mistakenly interpreted as the consequence of a diffuse off-axis hydrothermal
source, when it is the result of Mn deposition patterns and Mn diagenesis in
the sediments. Diffuse off-axis hydrothermal sources of Mn cannot be ruled out,
however.
Figure 4. Off-axis concentration distributions (T , T
, T , T
, T ) of the three water column phases of
hydrothermal Mn (nmol/L).
) of the three water column phases of
hydrothermal Mn (nmol/L).
The pMn plume (Figure 4b) shows the effects of particle settling, particle resuspension at the seafloor, and the exchange of pMn with the other water column Mn reservoirs. Concentrations of 0.4 nmol/L extend to nearly 200 km in an ocean where background pMn values are 0.1-0.3 nmol/L [e.g., Martin and Knauer, 1982, 1985; Landing and Bruland, 1987]. The axis of the pMn plume slopes downward, the consequence primarily of large particle settling. Resuspension of particles from the seafloor raise concentrations between the seafloor and plume axis.
The distribution of macroaggregate Mn is, perhaps, the most interesting (Figure 4c). Concentration has a maximum value ~0.05
nmol/L in a region a few tens of kilometers off axis. Since Mn flux to the sediments is
primarily in macroaggregate form, and that flux has a magnitude nearly equal to w C
C , Figure 4c suggests
that hydrothermal Mn will be deposited close to the ridge, but deposition will be small on
axis. The exact location of the off-axis maximum will depend on the values given model
parameters, but a reasonable range enforces near-ridge deposition of Mn. The pattern of
deposition is a consequence of the Mn having to pass through two phases before reaching
the sediments, and the time scales of those phase conversions of Mn in comparison to the
time scale of an off-axis distance divided by the advection velocity.
, Figure 4c suggests
that hydrothermal Mn will be deposited close to the ridge, but deposition will be small on
axis. The exact location of the off-axis maximum will depend on the values given model
parameters, but a reasonable range enforces near-ridge deposition of Mn. The pattern of
deposition is a consequence of the Mn having to pass through two phases before reaching
the sediments, and the time scales of those phase conversions of Mn in comparison to the
time scale of an off-axis distance divided by the advection velocity.
When sectioned vertically, as if taking a vertical cast, the profiles of dMn and pMn both show maxima at plume height and secondary maxima at the seafloor, just as do the observations [e.g., Cowen et al., 1986]. The vertical profiles of Mn in macroaggregate form have a much different shape. Vertical gradients are generally much slighter and so concentrations are likely to be more vertically uniform below plume height. If a vertical array of sediment traps could be moored below the plume, this model suggests that the hydrothermal flux of Mn into the traps should be nearly uniform. The prediction would be unwarranted very near the seafloor, however, because the model does not presently recognize the increased levels of turbulence in the benthic boundary layer. That increased vertical mixing should result in more near-bottom resuspension of particles, a process which is known to strongly effect near-bottom particle fluxes into traps [e.g., Walsh et al., 1988]. An actual flux measurement beneath a hydrothermal plume is made extremely difficult by the wafting three-dimensional nature of any real plume.
The weight fraction of Mn on particles, calculated from the quotient of the
Mn concentration and the particle concentration, is distributed, for fine particles
and macroaggregates, in the manner of Figures 4b
and 4c. The reason is that model particle
concentrations are taken to be spatially uniform, and so the quotient of T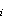 by C
by C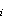 will have the off-axis
distributional shape of T
will have the off-axis
distributional shape of T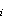 ,
where i = p or s. Weight fractions have maximum values
of ~1.2% Mn for fine particles and ~0.6% Mn for macroaggregates, both occurring
off axis. West of the ridge and 300 km downstream the particles bear only 0.1%
Mn by weight. Near-axis data of Dymond
and Roth [1988] on the Endeavor Ridge, for a sediment trap at a depth
corresponding to the upper part of the plume (1950 m) but presumably away from
the effects of resuspension, suggest Mn weight percent on trapped particles
of 0.1%. A more easily sampled trap of particles and hydrothermal Mn is the
sediment itself, the model results for which we now examine.
,
where i = p or s. Weight fractions have maximum values
of ~1.2% Mn for fine particles and ~0.6% Mn for macroaggregates, both occurring
off axis. West of the ridge and 300 km downstream the particles bear only 0.1%
Mn by weight. Near-axis data of Dymond
and Roth [1988] on the Endeavor Ridge, for a sediment trap at a depth
corresponding to the upper part of the plume (1950 m) but presumably away from
the effects of resuspension, suggest Mn weight percent on trapped particles
of 0.1%. A more easily sampled trap of particles and hydrothermal Mn is the
sediment itself, the model results for which we now examine.
Fluxes into model "sediment traps" are given by the expression w  T
T + w
+ w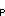 T
T . Since the first of these terms is very much
larger than the second, the principal contribution to Mn flux is from macroaggregates. A
horizontal transect of model Mn flux evaluated at the seafloor shows that the flux has a
maximum value of -10 mg/cm
. Since the first of these terms is very much
larger than the second, the principal contribution to Mn flux is from macroaggregates. A
horizontal transect of model Mn flux evaluated at the seafloor shows that the flux has a
maximum value of -10 mg/cm /kyr, occurring approximately
25 km off axis while on axis and far downstream the flux is more nearly 1 mg/cm
/kyr, occurring approximately
25 km off axis while on axis and far downstream the flux is more nearly 1 mg/cm /kyr. The distribution resembles in shape that shown in Figure 3c, the model Mn flux to sediments (equation
(11)). Those differ from Mn fluxes into sediment traps by the amounts of Mn remobilized in
the sediments and diffused back into the water column as dMn and by the amount of Mn
resuspended in particulate form. These rates are less, but for this model only slightly,
than Mn vertical fluxes indicated by model "traps."
/kyr. The distribution resembles in shape that shown in Figure 3c, the model Mn flux to sediments (equation
(11)). Those differ from Mn fluxes into sediment traps by the amounts of Mn remobilized in
the sediments and diffused back into the water column as dMn and by the amount of Mn
resuspended in particulate form. These rates are less, but for this model only slightly,
than Mn vertical fluxes indicated by model "traps."
Mn fluxes of these magnitudes have been measured in other hydrothermal areas
using actual sediment traps. Dymond
and Roth [1988], for the Endeavor Ridge and at 2 km from an active vent
field, found Mn fluxes at plume depth and below of 1.5-5 mg/cm /kyr.
The larger values may reflect the results of particle resuspension [e.g.,
Walsh et al., 1988]. Fischer
[1983] reported Mn fluxes 1.7 and 0.47 mg/cm
/kyr.
The larger values may reflect the results of particle resuspension [e.g.,
Walsh et al., 1988]. Fischer
[1983] reported Mn fluxes 1.7 and 0.47 mg/cm /kyr
at MANOP sites M and H, respectively, the first 25 km east of the EPR and the
second much farther away. Martin
et al. [1985] found Mn fluxes of 0.13-0.22 mg/cm
/kyr
at MANOP sites M and H, respectively, the first 25 km east of the EPR and the
second much farther away. Martin
et al. [1985] found Mn fluxes of 0.13-0.22 mg/cm /kyr
at two deep northeastern Pacific stations which we presume to be far from hydrothermal
influence.
/kyr
at two deep northeastern Pacific stations which we presume to be far from hydrothermal
influence.
Model Mn flux rates to the sediments and the measured weight percent of Mn in surficial sediment, though different quantities, was assumed to be similarly distributed. The likeness of the shape of the two distributions in Figure 3c was actually a condition achieved by model parameter adjustment, as will be discussed later. This approach leads to a relationship between the off-axis advection speed and the macroaggregate scavenging rate constant.
The underlying assumptions here require some discussion. The weight percent of Mn in surficial sediments depends on the rates of both Mn and sediment accumulation. Mn in the surficial layer of sediments (equation (11)) is determined not only by the Mn weight percent of the depositing particles, but also on the enrichment of the surficial sediments by upward migration of Mn from deeper in the core. The evidence for this diagenetic enrichment will be given below. A second factor, that of off-axis changes in the net sediment accumulation rate caused by the dissolution of carbonates and silicates at the seafloor, also has the potential for enlarging the Mn mass fraction in accumulating sediment compared to that in settling particles.
In the absence of sufficient data to make quantitative the consequences of
these several factors, we have been forced, for the present, to adopt off-axis
invariance of the benthic flux fraction  , the
degree of Mn enrichment of the surficial sediments by diagenetic processes,
and net sediment accumulation rates. Evidence bearing on the first comes from
Roth
and Dymond s [1989] compositional analysis of flux into sediment traps
at the Juan de Fuca Ridge. They found that organic matter mass fraction was
larger in traps near hydrothermal vents compared to those slightly (~2 km) away.
Thus there may be an off-axis dependence to organic flux, which, in turn, could
cause relative changes in the fraction (
, the
degree of Mn enrichment of the surficial sediments by diagenetic processes,
and net sediment accumulation rates. Evidence bearing on the first comes from
Roth
and Dymond s [1989] compositional analysis of flux into sediment traps
at the Juan de Fuca Ridge. They found that organic matter mass fraction was
larger in traps near hydrothermal vents compared to those slightly (~2 km) away.
Thus there may be an off-axis dependence to organic flux, which, in turn, could
cause relative changes in the fraction ( ) of
Mn remobilized and released back into the water column from a thin surficial
layer of sediments. It might also suggest, assuming uniformity over past time,
that there should be off-axis differences in the degree of Mn remobilization
at depth and enrichment near the surface of the sediment column. Patterns of
off-axis organic material flux are presently not available.
) of
Mn remobilized and released back into the water column from a thin surficial
layer of sediments. It might also suggest, assuming uniformity over past time,
that there should be off-axis differences in the degree of Mn remobilization
at depth and enrichment near the surface of the sediment column. Patterns of
off-axis organic material flux are presently not available.
Off-axis variations in sediment accumulation rates seem likely. Three cores (G. J.
Massoth, unpublished data, 1987) taken at 15.6, 43 and 308 km west of the ridge show the
weight percentage of CaCO measured at 2.5 cm
depth in the cores to be 46, 10, and 0.3%, respectively. Water depths at core locations
(Table 2) were 2635, 2970, and 3904 m. If carbonates were removed by dissolution in the
deepest core, if they were initially as much as 46% by weight as was found in the
near-axis core, and if carbonate dissolution is the only process altering sediment
accumulation rate, the sediment accumulation rate at 308 km could be only one half those
at 15 km off axis. Other rate altering processes, whether close to or at substantial
distances from the ridge crest, require corresponding consideration. Reducing the net
sedimentation rate would have the effect of increasing the weight fraction of Mn in the
sediments for the same incident flux of Mn. If sediment accumulates more slowly the larger
the distance off axis, the model Mn depositional flux curve (Figure
3c) will need to be made to decrease more quickly with off-axis distance than
it now does so that the shapes of the Mn percent weight distributions from model and core
data will agree. Decreasing rates of actual sediment accumulation off axis will cause
hydrothermal Mn deposition to be more ridge oriented than even the present analysis
suggests.
measured at 2.5 cm
depth in the cores to be 46, 10, and 0.3%, respectively. Water depths at core locations
(Table 2) were 2635, 2970, and 3904 m. If carbonates were removed by dissolution in the
deepest core, if they were initially as much as 46% by weight as was found in the
near-axis core, and if carbonate dissolution is the only process altering sediment
accumulation rate, the sediment accumulation rate at 308 km could be only one half those
at 15 km off axis. Other rate altering processes, whether close to or at substantial
distances from the ridge crest, require corresponding consideration. Reducing the net
sedimentation rate would have the effect of increasing the weight fraction of Mn in the
sediments for the same incident flux of Mn. If sediment accumulates more slowly the larger
the distance off axis, the model Mn depositional flux curve (Figure
3c) will need to be made to decrease more quickly with off-axis distance than
it now does so that the shapes of the Mn percent weight distributions from model and core
data will agree. Decreasing rates of actual sediment accumulation off axis will cause
hydrothermal Mn deposition to be more ridge oriented than even the present analysis
suggests.
The difference in the magnitudes (but not shape) of the model and data Mn weight
fractions is caused primarily, we believe, by diagenetic processes in the sediment
column. The maximum measured weight percent of Mn in sediments (Figure
3c) is ~4.7%, but the model maximum value, taking a spatially invariant
sedimentation flux of 1.6g/cm /kyr [Dymond
and Roth, 1988], amounts to ~0.6%. The model particles bear only about
15% the amount of Mn as found in the surficial sediments. At depth (40 cm) in
the cores taken 15.6, 30, 43, and 308 km from the ridge, the Mn weight percents
are 0.2, 0.6, 0.6, and 0.1% (G. J. Massoth, unpublished data, 1987). These values
are only 13-20% of those near the surface (2.5 cm) of the core. Reduction of
Mn in an anoxic layer of sediments, dMn migration upward, and Mn reoxidation
in the upper layer of sediments would cause such profiles. Pore water nutrient
and Mn profiles from cores to the west of the ridge in Cascadia Basin [Jones
and Murray, 1985] suggest reducing conditions at depth in the sediments
and an oxic surface layer where dMn is rescavenged by particles.
/kyr [Dymond
and Roth, 1988], amounts to ~0.6%. The model particles bear only about
15% the amount of Mn as found in the surficial sediments. At depth (40 cm) in
the cores taken 15.6, 30, 43, and 308 km from the ridge, the Mn weight percents
are 0.2, 0.6, 0.6, and 0.1% (G. J. Massoth, unpublished data, 1987). These values
are only 13-20% of those near the surface (2.5 cm) of the core. Reduction of
Mn in an anoxic layer of sediments, dMn migration upward, and Mn reoxidation
in the upper layer of sediments would cause such profiles. Pore water nutrient
and Mn profiles from cores to the west of the ridge in Cascadia Basin [Jones
and Murray, 1985] suggest reducing conditions at depth in the sediments
and an oxic surface layer where dMn is rescavenged by particles.
The model benthic flux of dMn from the sediments back into the water column
(equation (5)) will have a distributional shape similar to that in Figure
3c. Magnitudes are approximately 10% those of the depositional flux
(Figure 3c); the maximum value of the
flux is -18 nmol/cm /yr under the model conditions
of Table 3. From two-point measurements at the top of MANOP Site M cores, Heggie
et al. [1986] inferred benthic flux rates for Mn of 8-18 nmol/cm
/yr under the model conditions
of Table 3. From two-point measurements at the top of MANOP Site M cores, Heggie
et al. [1986] inferred benthic flux rates for Mn of 8-18 nmol/cm /yr.
In the Guaymas Basin, where reducing conditions exist in sediments very near
surface, Campbell
et al. [1988] inferred flux rates of 130 ± 60 nmol/cm
/yr.
In the Guaymas Basin, where reducing conditions exist in sediments very near
surface, Campbell
et al. [1988] inferred flux rates of 130 ± 60 nmol/cm /yr
using similar analyses. Since neighboring Cascadia Basin surface sediments are
more oxidizing than reducing [Jones
and Murray, 1985], the model benthic fluxes of dMn seem to have a reasonable
magnitude range.
/yr
using similar analyses. Since neighboring Cascadia Basin surface sediments are
more oxidizing than reducing [Jones
and Murray, 1985], the model benthic fluxes of dMn seem to have a reasonable
magnitude range.
The hydrothermal Mn source flux, Q ,
was determined by adjustment so that dMn and pMn values near the ridge would
have magnitudes similar to those measured (Figures
1a and 1b). The resulting value
of Q
,
was determined by adjustment so that dMn and pMn values near the ridge would
have magnitudes similar to those measured (Figures
1a and 1b). The resulting value
of Q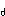 was 4.2 × 10
was 4.2 × 10 g/m/s (1.4 × 10
g/m/s (1.4 × 10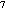 g/km/yr). Baker
and Massoth [1986] estimated the flux of Mn averaged over a 10-km-long
section of the southern JDFR at 11 × 10
g/km/yr). Baker
and Massoth [1986] estimated the flux of Mn averaged over a 10-km-long
section of the southern JDFR at 11 × 10 g/m/s, a value nearly 3 times that suggested by this model. The differences
in rates could be due to the shorter averaging time represented by the Baker
and Massoth [1986] analysis, or to spatial differences in hydrothermal
activity along the ridge crest. At the EPR, Lyle
[1976] estimated a Mn flux rate of 5 × 10
g/m/s, a value nearly 3 times that suggested by this model. The differences
in rates could be due to the shorter averaging time represented by the Baker
and Massoth [1986] analysis, or to spatial differences in hydrothermal
activity along the ridge crest. At the EPR, Lyle
[1976] estimated a Mn flux rate of 5 × 10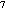 g/km/yr, approximately 4 times that suggested by this model from JDFR data.
The larger weight fraction of Mn in sediments at the EPR compared to the JDFR
may make the difference meaningful.
g/km/yr, approximately 4 times that suggested by this model from JDFR data.
The larger weight fraction of Mn in sediments at the EPR compared to the JDFR
may make the difference meaningful.
The sensitivity of results to changes in a number of parameters away from the values of
Table 3 was examined. First k was
given a value of (1080 days)
was
given a value of (1080 days) , so that k
, so that k /k
/k would be 3 rather than 1/3. Mn remobilization from capsuled
bacteria then occurs over a period 3 times as long as the time scale for Mn scavenging.
Exchange equilibrium tilts more toward the direction of pMn. The resulting plume
distributions show less dMn at distance from the ridge; higher pMn concentrations to a
distance of ~150 km; higher flux of Mn to the sediments over the initial 150 km; less pMn
and lower flux of Mn to the seafloor beyond 150 km; concentrations reduced for dMn and
slightly elevated for pMn near the seafloor. The available data for hydrothermal Mn at the
JDFR cannot be used to differentiate between the two values (0.33 and 3.0) used for k
would be 3 rather than 1/3. Mn remobilization from capsuled
bacteria then occurs over a period 3 times as long as the time scale for Mn scavenging.
Exchange equilibrium tilts more toward the direction of pMn. The resulting plume
distributions show less dMn at distance from the ridge; higher pMn concentrations to a
distance of ~150 km; higher flux of Mn to the sediments over the initial 150 km; less pMn
and lower flux of Mn to the seafloor beyond 150 km; concentrations reduced for dMn and
slightly elevated for pMn near the seafloor. The available data for hydrothermal Mn at the
JDFR cannot be used to differentiate between the two values (0.33 and 3.0) used for k /k
/k .
.
A comparison was then made of distributions when T ( = 1/k
( = 1/k )
equals 30, 60, and 180 days. The smaller value of T
)
equals 30, 60, and 180 days. The smaller value of T forces more rapid fine particle scavenging by macroaggregates
while larger value indicates the opposite. For T
forces more rapid fine particle scavenging by macroaggregates
while larger value indicates the opposite. For T = 30 days, dMn and pMn concentrations in the water column are
about half of what they are for T
= 30 days, dMn and pMn concentrations in the water column are
about half of what they are for T = 60
days, the central T
= 60
days, the central T value of the
analysis (Table 3). Any Mn taken up by capsules is more quickly removed to the sediments.
Because the rate conversion of dMn to pMn was fixed as before, however, the rate of
formation of pMn is unchanged. The deposition pattern is more sharply peaked than that of Figure 3c, but the off-axis location of the maximum in
the distribution is nearly the same. When T
value of the
analysis (Table 3). Any Mn taken up by capsules is more quickly removed to the sediments.
Because the rate conversion of dMn to pMn was fixed as before, however, the rate of
formation of pMn is unchanged. The deposition pattern is more sharply peaked than that of Figure 3c, but the off-axis location of the maximum in
the distribution is nearly the same. When T = 180 days, remobilization of Mn from capsules (T
= 180 days, remobilization of Mn from capsules (T = 120 days, Table 2) plays more of a role. In
this case, pMn persists in the water column much longer, dMn stays elevated to a much
larger distance, and the deposition pattern is far less peaked than that of Figure 3c. In order for the shape of the model Mn
deposition pattern to resemble the shape of the measured Mn weight percent in sediments (Figure 3c) for this T
= 120 days, Table 2) plays more of a role. In
this case, pMn persists in the water column much longer, dMn stays elevated to a much
larger distance, and the deposition pattern is far less peaked than that of Figure 3c. In order for the shape of the model Mn
deposition pattern to resemble the shape of the measured Mn weight percent in sediments (Figure 3c) for this T , the off-axis advection speed would need to be very much less
than 0.2 cm/s.
, the off-axis advection speed would need to be very much less
than 0.2 cm/s.
That relationship between T and u
was quantified by comparing the misfit of the model Mn depositional flux distribution to
the Mn weight percent data for sediments under various values of the two parameters. To
understand how this was done, consider the differences in model deposition patterns when
parameters are fixed as in Table 3, except K
and u
was quantified by comparing the misfit of the model Mn depositional flux distribution to
the Mn weight percent data for sediments under various values of the two parameters. To
understand how this was done, consider the differences in model deposition patterns when
parameters are fixed as in Table 3, except K = 0, and u is allowed to vary (Figure 5a). The curves of Figure
5a represent Mn fluxes to the sediments, but flux scales are not given; the
left-hand scale refers to the data only. As stated earlier in regard to Figure 3c, these fluxes should have the same
distributional shape as the measured weight percent of Mn in the sediments (boxes, Figure 5a). To make quantitative the differences
between the modeled and measured distributions, each flux curve was first rescaled so that
the maximum flux had the same ordinate value as the maximum measured weight percent. A
sum-of-squared-error measure of misfit was then evaluated. Only points at off-axis
distances at and beyond that corresponding to the maximum ordinate data value were
included in the sum, however. Otherwise, the difference errors for points at distances
less than 20 km (Figure 5a) dominate the misfit sum,
while the selection of "best fit" is more fairly based on the difference errors
for points beyond 20 km (Figure 5c). It is
reasonably clear from inspection (Figure 5a) that a u
value of 0.15 cm/s results in a flux distribution having the essential features of the
measured Mn weight percent distribution in the sediments, when the other parameters are
fixed as they are. The sum-of-squared-error measure encompassing all data points, on the
other hand, would result in a misfit measure that could not differentiate between the
quality of the fit provided by any curve in Figure 5a.
= 0, and u is allowed to vary (Figure 5a). The curves of Figure
5a represent Mn fluxes to the sediments, but flux scales are not given; the
left-hand scale refers to the data only. As stated earlier in regard to Figure 3c, these fluxes should have the same
distributional shape as the measured weight percent of Mn in the sediments (boxes, Figure 5a). To make quantitative the differences
between the modeled and measured distributions, each flux curve was first rescaled so that
the maximum flux had the same ordinate value as the maximum measured weight percent. A
sum-of-squared-error measure of misfit was then evaluated. Only points at off-axis
distances at and beyond that corresponding to the maximum ordinate data value were
included in the sum, however. Otherwise, the difference errors for points at distances
less than 20 km (Figure 5a) dominate the misfit sum,
while the selection of "best fit" is more fairly based on the difference errors
for points beyond 20 km (Figure 5c). It is
reasonably clear from inspection (Figure 5a) that a u
value of 0.15 cm/s results in a flux distribution having the essential features of the
measured Mn weight percent distribution in the sediments, when the other parameters are
fixed as they are. The sum-of-squared-error measure encompassing all data points, on the
other hand, would result in a misfit measure that could not differentiate between the
quality of the fit provided by any curve in Figure 5a.
Figure 5. (a) Distributions of model Mn flux to sediments (curves) for
varying off-axis advection velocities when T = 60 days. Superimposed on model distributions are the
measured weight percent of Mn in surficial sediments (squares) from Table 2. Flux
distributions have been individually rescaled so that maximum has the same ordinate value
as the data maximum; flux scales are consequently not shown. The degree of misfit between
each distribution and the measured weight percents was calculated as the sum of squared
errors, as described in the text. (b) The resulting sum-of-squared-error surfaces
for a range of u and T
= 60 days. Superimposed on model distributions are the
measured weight percent of Mn in surficial sediments (squares) from Table 2. Flux
distributions have been individually rescaled so that maximum has the same ordinate value
as the data maximum; flux scales are consequently not shown. The degree of misfit between
each distribution and the measured weight percents was calculated as the sum of squared
errors, as described in the text. (b) The resulting sum-of-squared-error surfaces
for a range of u and T values
when k
values
when k /k
/k equals 0.33 and (c) when k
equals 0.33 and (c) when k /k
/k equals
3.
equals
3.
Values for the sum of the squared error were evaluated in this way for a range of u
and T values and for two values of the
k
values and for two values of the
k /k
/k ratio. The resulting error values were contoured in the u,
T
ratio. The resulting error values were contoured in the u,
T plane (Figure
5b and 5c). For both values of k
plane (Figure
5b and 5c). For both values of k /k
/k , the error surface shows a trough, indicating that nearly
equivalent deposition distributions can be obtained for a number of u and T
, the error surface shows a trough, indicating that nearly
equivalent deposition distributions can be obtained for a number of u and T pairs. T
pairs. T and u are also anticorrelated. If T
and u are also anticorrelated. If T is small, i.e., rapid macroaggregate scavenging
of fine particles, the observed distribution of Mn in sediments is consistent only with a
larger (e.g., 0.25 cm/s) off-axis component of advection. For a smaller velocity component
(e.g., 0.1 cm/s), rapid (T
is small, i.e., rapid macroaggregate scavenging
of fine particles, the observed distribution of Mn in sediments is consistent only with a
larger (e.g., 0.25 cm/s) off-axis component of advection. For a smaller velocity component
(e.g., 0.1 cm/s), rapid (T = 20 days)
macroaggregate scavenging would cause the Mn to be deposited too close to the ridge.
Extending the deposition pattern off axis to resemble the data for small u (e.g.,
0.1 cm/s) requires that the macroaggregate scavenging proceed at a slower rate (e.g., T
= 20 days)
macroaggregate scavenging would cause the Mn to be deposited too close to the ridge.
Extending the deposition pattern off axis to resemble the data for small u (e.g.,
0.1 cm/s) requires that the macroaggregate scavenging proceed at a slower rate (e.g., T = 100 days, Figure 5b).
This general picture is not much changed if k
= 100 days, Figure 5b).
This general picture is not much changed if k /k
/k = 3.0 (Figure 5c). Since it seems reasonable to think that T
= 3.0 (Figure 5c). Since it seems reasonable to think that T has a time scale of the order of weeks to months,
based on currently available reports, the results (Figures 5b
and 5c) make it seem likely that u is in the
range 0.1 to 0.3 cm/s.
has a time scale of the order of weeks to months,
based on currently available reports, the results (Figures 5b
and 5c) make it seem likely that u is in the
range 0.1 to 0.3 cm/s.
The residence time of hydrothermal Mn in the water column has been studied with the
model under the given parameter values (Table 3). The time dependent solution of equations
(1)-(3), with horizontal transport terms set to zero, was examined for a unit impulse
discharge of dMn at plume height. The constants u and K can be set to zero because, in calculating residence times,
the horizontal location of the tracer is immaterial. Water column concentrations of dMn,
pMn, macroaggregate Mn, and Mn deposited in the sediment were calculated in time over a
period of 1400 days. Water column concentrations were integrated with height and all
results expressed as fractions of the original amount of Mn discharged. The consequent
time histories (Figure 6) show the passage of Mn through
all the three water column stages and into the sediments. The term residence time can be
defined in many different ways. In simple systems undergoing exponential loss, the time
for the concentration to be reduced to 1/e (37%) its initial value can be called
the residence time. The same definition is used here: residence time will mean that time
at which only 37% of the initial amount of Mn remains in the water column.
can be set to zero because, in calculating residence times,
the horizontal location of the tracer is immaterial. Water column concentrations of dMn,
pMn, macroaggregate Mn, and Mn deposited in the sediment were calculated in time over a
period of 1400 days. Water column concentrations were integrated with height and all
results expressed as fractions of the original amount of Mn discharged. The consequent
time histories (Figure 6) show the passage of Mn through
all the three water column stages and into the sediments. The term residence time can be
defined in many different ways. In simple systems undergoing exponential loss, the time
for the concentration to be reduced to 1/e (37%) its initial value can be called
the residence time. The same definition is used here: residence time will mean that time
at which only 37% of the initial amount of Mn remains in the water column.
Figure 6. Percent of initial discharge in each of four Mn reservoirs as a function
of time. Parameter settings are as in Table 3, but with (a) k /k
/k = 0.33 and (b) k
= 0.33 and (b) k /k
/k = 3.
= 3.
The time histories (Figure 6a) show the slow conversion of dMn to other Mn phases. After 100 days, more than 80% of the Mn remains in dissolved form, while fine particulate Mn accounts for only -10% of Mn stock. Because of this slow exchange, it is to be expected that near the ridge Mn will be seen primarily in dissolved form. By 700 days, dMn is reduced to 37% of the initial concentration and by 750 days, the residence time, 63% of the initial Mn discharge has been deposited in the sediments. Note, however, that even after 1400 days more than 10% of the stock remains as dMn. If the off-axis advection is 0.2 cm/s (Table 3), for example, dMn levels should exceed background dMn levels several fold even beyond 240 km from the ridge (Figure 4a).
These results are somewhat changed when the k /k
/k is set
to 3 (Figure 6b). Remobilization of Mn from capsule
bacteria is less favored, so the dMn decreases more quickly. Now at 700 days, little more
than 20% of the Mn stock is in dMn form. The residence time of Mn is shortened to ~500
days.
is set
to 3 (Figure 6b). Remobilization of Mn from capsule
bacteria is less favored, so the dMn decreases more quickly. Now at 700 days, little more
than 20% of the Mn stock is in dMn form. The residence time of Mn is shortened to ~500
days.
Figures 6a and 6b show too that the hydrothermal fine particulate Mn stock never exceeds more than -15% of the total hydrothermal Mn stock. Macroaggregate Mn is never more than 0.5%, yet effectively all Mn passes through this stage to be deposited in the sediments. Macroaggregate concentrations mirror the distribution of Mn flux to the sediment (Figure 4c) under exchange of time and space axes possible in the case of steady advection.
Interestingly, under these model conditions, by 1400 days (240 km when u = 0.2 cm/s) more than 80% of the Mn is deposited in the sediments. This means that much of the hydrothermal Mn is unavailable to the oceans over larger scales. Still dMn concentrations are many times background beyond that distance (Figure 4a). Under actual conditions, the fraction deposited may not be quite as high as depicted in Figure 6. Off axis, the bottom falls away from ridge crest depths and longer settling distance may have the effect of lengthening depositional time scales. On the other hand, the sediment distribution pattern of Figure 1c will still have to be accommodated, so the effect of sloping bathymetry may only just force quickened scavenging or larger settling velocities. The consequences of variable depth on the results has not yet been studied. With some of the processes underlying the model, e.g., macroaggregate scavenging and release, now so poorly understood, it does not seem warranted at this point.
This two-stage Mn scavenging model provides a framework for integrating the exchange and dispersion processes that transport hydrothermal Mn from ridge crest to the adjacent sediments. The model links these processes presently recognized as important: Mn exchange from dissolved to fine particle (capsuled bacteria) form, fine particle exchange with large more loosely aggregated particles, particle resuspension at the seafloor, benthic flux of dissolved Mn from sediments, and physical transport by particle settling, advection, and turbulent diffusion. As a framework, the model permits concentration and fluxes in the water column and in and out of the sediments all to be quantitatively connected. Beyond its use as an interpolating tool, the model also points to regions of the water column and to component processes where additional, fruitful measurements to define the deposition of Mn are likely to be acquired. These must surely include macroaggregate distributions and rates of exchange with the fine particle population, and Mn distributions in separate phases near the seafloor.
While the model is not specific to hydrothermal regions, one advantage a hydrothermal region provides is that the ridge crest source is a localized one. This makes hydrothermal Mn useful as a tracer, albeit nonconservative, of physical and sedimentalogical processes in the deep ocean. Biogeochemical exchanges must be acknowledged, as in this model, to extract that kind of information, however. The model and data together suggest that most of the hydrothermal Mn is deposited within several hundred kilometers of the ridge, making most of the hydrothermal Mn unavailable to the distal ocean. Still there is sufficient hydrothermal Mn flux beyond that distance to elevate Mn water column concentrations several times above background levels.
Inferences based on the model and the presently available data must be considered only semiquantitative. Our present limited understanding of component processes and the difficulty of sampling, time-dependent three-dimensional hydrothermal plumes presently disallow a more elaborate model or a more comprehensive comparison of model and observations. For example, any model with just two particle classes is minimal because the diversity of particle types in the ocean is large. Going beyond this minimal scheme, however, will require exchange rates and settling velocities for a larger set of particle classes, information not likely to be quickly acquired. Even for two bulk particle classes, we are only beginning to interpret the time scales of exchange. Better definition of all model processes and parameters await future measurements.
Despite its semiquantitative nature, the model seems to contain many of the important elements of cycling of Mn in hydrothermal regions. It should serve as a useful tool to examine additional observations and to focus the need to examine the basic elements of Mn transport. The challenge is to cautiously interpret hard to acquire, limited tracer measurements; by connecting a diversity of measurements, this type of model can help do that.
Acknowledgments. We thank Kevin Roe and Geoff Lebon for determination of dissolved and particulate Mn values and Sharon Roth for many helpful comments on the manuscript. Contribution 1285 from NOAA/Pacific Marine Environmental Laboratory. Contribution 2707 from SOEST/University of Hawaii.
Alldredge, A. L., and C. Gotschalk, In situ settling behavior of marine snow, Limnol. Oceanogr., 33(3), 339-351, 1988.
Alldredge, A. L., and M. Silver, Characteristics, dynamics, and significance of marine snow, Prog. Oceanogr., 20, 41-82, 1988.
Asper, V. L., Accelerated settling of particulate matter by "marine snow" aggregates, Ph.D. dissertation, 189 pp., Woods Hole Oceanogr. Inst., Woods Hole, Mass., 1986.
Asper, V. L., Measuring the flux and sinking speed of marine snow at depth, Deep Sea Res., 34, 1-17, 1987.
Bacon, M. P., C.-A. Huh, A. P. Fleer, and W. G. Dueser, Seasonality in the flux of natural radionucleides and plutonium in the deep Sargasso Sea, Deep Sea Res., 32(3), 273-286, 1985.
Baker, E. T., and G. J. Massoth, Hydrothermal plume measurements: A regional perspective, Science, 234, 980-982, 1986.
Baker, E. T., and G. J. Massoth, Characteristics of hydrothermal plumes from two vent fields on the Juan de Fuca Ridge, northeast Pacific Ocean, Earth Planet. Sci. Lett., 85, 59-73, 1987.
Baker, E. T., J. W. Lavelle, R. A. Feely, G. J. Massoth, S. L. Walker, and J. E. Lupton, Episodic venting of hydrothermal fluids from the Juan de Fuca Ridge, J. Geophys. Res., 94, 9237-9250, 1989.
Bishop, J. K., J. M. Edmond, D. R. Ketten, M. P. Bacon, and W. B. Silker, Chemistry, biology, and vertical flux of particulate matter from the upper 400 m of the equatorial Atlantic Ocean, Deep Sea Res., 24(6), 511-548, 1977.
Bostrom, K., and M. N. A. Peterson, The origin of aluminum-poor ferromanganoan sediments in areas of high heat flow on the East Pacific Rise, Mar. Geol., 7(5), 427-447, 1969.
Campbell, A. C., J. M. Gieskes, J. E. Lupton, and P. F. Lonsdale, Manganese geochemistry in the Guaymas Basin, Gulf of California, Geochim. Cosmochim. Acta, 52, 345-357, 1988.
Cannon, G. A., D. J. Pashinski, and M. Lemon, Middepth flow near hydrothermal venting sites on the Southern Juan de Fuca Ridge, J. Geophys. Res., 96(C7), 12,815-12,831, 1991.
Clegg, S. L., and M. Whitfield, A generalized model for the scavenging of trace metals in the ocean, I. Particle cycling, Deep Sea Res., 37(5), 809-832, 1990.
Coale, K. H., C. Chin, G. J. Massoth, K. S. Johnson, and E. T. Baker, In situ mapping of dissolved iron and manganese in hydrothermal plumes, Nature, 352, 325-328, 1991.
Cowen, J. P., and Y.-H. Li, The influence of a changing bacterial community on trace metal scavenging in a deep-sea particle plume, J. Mar. Res., 49(3), 517-542, 1991.
Cowen, J. P., G. J. Massoth, and E. T. Baker, Bacterial scavenging of Mn and Fe in the mid- to far-field hydrothermal particle plume, Nature, 322, 169-171, 1986.
Cowen, J. P., G. J. Massoth, and R. A. Feely, Scavenging rates of dissolved manganese in a hydrothermal vent plume, Deep Sea Res., 37(10), 1619-1637, 1990.
Deuser, W. G., E. H. Ross, and R. F. Anderson, Seasonality in the supply of sediment to the deep Sargasso Sea and implications for the rapid transfer of matter to the deep ocean, Deep Sea Res., 28A(5), 495-505, 1981.
Duncan, J. R., Jr., Late pleistocene and postglacial sedimentation and stratigraphy of deep-sea environments off Oregon, Ph.D. thesis, 222 pp., Oreg. State Univ., Corvallis, 1968.
Dymond, J., Geochemistry of Nazca plate surface sediments: An evaluation of hydrothermal, biogenic, detrital, and hydrogenous sources, Geol. Soc. Am. Mem., 154, 133-173, 1981.
Dymond, J., and S. Roth, Plume dispersed hydrothermal particles: A time-series of settling flux from the Endeavor Ridge using moored sensors, Geochim. Cosmochim. Acta, 52, 2525-2536, 1988.
Feely, R. A., G. J. Massoth, and G. T. Lebon, Sampling of marine particulate matter and analysis by x-ray flourescence spectrometry, in Marine Particles: Analysis and Characterization, Geophys. Monogr. Ser., vol. 63, edited by D. C. Hurd and D. W. Spencer, pp. 251-257, AGU, Washington, D. C., 1991.
Feely, R. A., G. J. Massoth, E. T. Baker, G. T. Lebon, and T. L. Geiselman, Tracking the dispersal of hydrothermal plumes from the Juan de Fuca Ridge using suspended matter compositions, J. Geophys. Res., 97(B3), 3457-3468, 1992.
Fischer, K. B., Particle fluxes in the eastern tropical Pacific Ocean -- Sources and fluxes, Ph.D. thesis, 225 pp., Oreg. State Univ., Corvallis, 1983.
Fowler, S. W., and G. A. Knauer, Role of large particles in the transport of elements and organic compounds through the oceanic water column, Prog. Oceanogr., 16, 147-194, 1986.
Gargett, A. E., Vertical eddy diffusivity in the ocean interior, J. Mar. Res., 42, 359-393, 1984.
Garrett, C., Mixing in the ocean interior, Dyn. Atmos. Oceans, 3, 239-265, 1979.
Heggie, D., D. Kahn, and K. Fischer, Trace metals in metalliferous sediments, MANOP Site M, Interfacial pore water profiles, Earth Planet. Sci. Lett., 80(1/2), 106-116, 1986.
Honeyman, B. D., and P. Santschi, A brownian-pumping model for oceanic trace metal scavenging: Evidence from Th isotopes, J. Mar. Res., 47(4), 951-992, 1989.
Honeyman, B. D., L. S. Balistrieri, and J. W. Murray, Oceanic trace metal scavenging: The importance of particle scavenging, Deep Sea Res., 35(2), 227-246, 1988.
Honjo, S., Material fluxes and modes of sedimentation in the mesopelagic and bathypelagic zones, J. Mar. Res., 38, 53-97, 1980.
Honjo, S., Study of ocean fluxes in time and space by bottom tethered sediment trap arrays: A recommendation, in Global Ocean Flux Study, Proceedings of a Workshop, pp. 306-324, National Academy Press, Washington D. C., 1985.
Jones, C. J., and J. W. Murray, The geochemistry of manganese in the northeast Pacific Ocean off Washington, USA, Limnol. Oceanogr., 30(1), 81-92, 1985.
Kalhorn, S., and S. Emerson, The oxidation of manganese in surface sediments of the deep sea, Geochim. Cosmochim. Acta, 48, 897-902, 1984.
Klinkhammer, G., and A. Hudson, Dispersal patterns for hydrothermal plumes in the South Pacific using manganese as a tracer, Earth Planet. Sci. Lett., 79, 241-249, 1986.
Klinkhammer, G., G. P. Rona, M. Greaves, and H. Elderfield, Hydrothermal Mn plumes in the Mid-Atlantic Ridge rift valley, Nature, 314, 727-731, 1985.
Landing, W. M., and K. W. Bruland, The contrasting biogeochemistry of iron and manganese in the Pacific Ocean, Geochim. Cosmochim. Acta, 51, 29-43, 1987.
Lavelle, J. W., H. O. Mofjeld, and E. T. Baker, An in situ erosion rate for a fine-grained marine sediment, J. Geophys. Res, 89(C4), 6543-6552, 1984.
Lavelle, J. W., C. N. Cudaback, A. J. Paulson, and J. W. Murray, A rate for the scavenging of fine particles by macroaggregates in a deep estuary, J. Geophys. Res., 96(C1), 783-790, 1991.
Lupton, J. E., and H. Craig, A major helium-3 source at 15°S on the East Pacific Rise, Science, 214, 13-18, 1981.
Lyle, M., Estimation of hydrothermal manganese input into the ocean, Geology, 4, 733-736, 1976.
Lyle, M. W., R. M. Owen, and M. Leinen, History of hydrothermal sedimentation at the East Pacific Rise, 19°S, Proc. Ocean Drill. Program Initial Rep., 92, 585-596, 1986.
Martin, J. H., and G. A. Knauer, Manganese cycling in northeast Pacific equatorial waters, J. Mar. Res., 40(4), 1213-1225, 1982.
Martin, J. H., and G. A. Knauer, Lateral transport of Mn in the northeast Pacific Gyre oxygen minimum, Nature, 314(11), 524-526, 1985.
Martin, J. H., G. A. Knauer, and W. W. Broenkow, VERTEX: The lateral transport of manganese in the northeast Pacific, Deep Sea Res., 32(11), 1405-1427, 1985.
Massoth, G. J., E. T. Baker, R. A. Feely, and H. C. Curl, Jr., Hydrothermal signal away from the southern Juan de Fuca Ridge (abstract), Eos Trans. AGU, 64(45), 1112, 1984.
McCave, I. N., Vertical flux of particles in the ocean, Deep Sea Res., 22, 491-502, 1975.
Morse, P. M., and H. Feshbach, Methods of Theoretical Physics, Part I, 997 pp., McGraw-Hill, New York, 1953.
Murname, R. J., J. L. Sarmiento, and M. P. Bacon, Thorium isotopes, particle cycling models, and inverse calculations of model rate constants, J. Geophys. Res., 95(C9), 16,195-16,206, 1990.
Nozaki, Y., H.-S. Yang, and M. Yamada, Scavenging of thorium in the ocean, J. Geophys. Res., 92(C1), 772-778, 1987.
Nyffeler, U. P., Y.-H. Li, and P. H. Santschi, A kinetic approach to describe trace-element distribution between particles and solution in natural aquatic systems, Geochim. Cosmochim. Acta, 48, 1513-1522, 1984.
Okubo, A., Oceanic diffusion diagrams, Deep Sea Res., 18, 789-802, 1971.
Parthenaides, E., Results of recent investigations on the erosion and deposition of cohesive soils, in Sedimentation, edited by H. W. Shen, pp. 20-1-20-38, H. W. Shen, Fort Collins, Colo., 1972.
Reid, J., On the mid-depth circulation of the world ocean, in Evolution of Physical Oceanography, edited by B. A. Warren and C. Wunsch, pp. 70-111, MIT Press, Cambridge, Mass., 1981.
Rona, P., Ocean ridge crest processes, Rev. Geophys., 25(5), 1089-1114, 1987.
Roth, S., and J. Dymond, Transport and settling of organic material in a deep-sea hydrothermal plume: Evidence from particle flux measurements, Deep Sea Res., 36(8), 1237-1254, 1989.
Silver, M. W., and A. L. Alldredge, Bathypelagic marine snow: Deep-sea algal and detrital community, J. Mar. Res., 39(3), 501-530, 1981.
Stommel, H., Is the South Pacific helium-3 plume dynamically active?, Earth Planet. Sci. Lett., 61, 63-67, 1982.
Walker, S. L., and E. T. Baker, Particle-size distributions within hydrothermal plumes over the Juan de Fuca Ridge, Mar. Geol., 78, 217-226, 1988.
Walsh, I., K. Fischer, D. Murray, and J. Dymond, Evidence for resuspension of rebound particles from near-bottom sediment traps, Deep Sea Res., 35(1), 59-70, 1988.
Return to Abstract