U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
Ten-year time series of sea surface temperature (SST), 20°C depth, and zonal winds
measured by moored buoys across the equatorial Pacific are used to define the
intraseasonal (30- to 90-day period) Kelvin waves. The Kelvin waves are observed to be
forced west of the date line and propagate at a speed of
The purpose of this paper is to document the connection between intraseasonal (30-90 days) Kelvin waves in the equatorial Pacific and planetary-scale, eastward-propagating intraseasonal convection fluctuations in the tropical atmosphere (the Madden-Julian Oscillation). The connection is of interest because it suggests that the frequently observed intraseasonal waves can be viewed as a manifestation of a global phenomenon, not strictly internal to the Pacific. We then show that intraseasonal fluctuations in the ocean and atmosphere exhibit consistent low-frequency modulation associated with the annual eastward march of convection and with El Niño-Southern Oscillation (ENSO) variability. This variation of the amplitude of the intraseasonal frequency band could be one way in which the Pacific is affected by low-frequency signals originating outside the basin and may provide a mechanism whereby the Pacific feels climatic events originating in the Indian Ocean and south Asian monsoon circulation. We use the extensive TOGA-TAO buoy network (see section 2) to observe the life cycle of the Kelvin waves and the wind forcing that creates them.
A series of papers have described and diagnosed the dynamics of the intraseasonal oceanic Kelvin waves. Spillane et al. [1987] used sea level observations to show that poleward-propagating intraseasonal variability was detectable all along the coast of the Americas from California to Peru. Enfield [1987] extended this analysis and found that the source of the coastal variability was first baroclinic mode equatorial Kelvin waves forced by western Pacific winds. He noted the apparent association with atmospheric intraseasonal variability and found that the oceanic waves seemed to be best developed during the onset of the 1982-1983 El Niño but were relatively weak in the subsequent 2 years. Remarking on this interannual variation of the signal, Enfield [1987] wondered if there was any connection to the ENSO cycle. McPhaden and Taft [1988] analyzed temperature, wind, and current observations from moored buoys at 140°W and 110°W (an earlier set of the same buoy data used in the present study) and found that intraseasonal variability was prominent in subsurface temperature and zonal currents, but not in meridional currents or eastern Pacific winds, consistent with the interpretation in terms of remotely forced Kelvin waves. Johnson and McPhaden [1993a] studied the vertical and meridional structure of the Kelvin waves at 140°W, 124°W, and 110°W using frequency-domain empirical orthogonal functions (EOFs) and found important differences between the observed characteristics of the intraseasonal variability and the structures expected from linear Kelvin wave theory. These discrepancies were explained by interactions between the waves and the mean zonal current/temperature regime. In particular, intraseasonal sea surface temperature (SST) variations in the equatorial cold tongue were shown to be related to zonal advection by these Kelvin waves. Johnson and McPhaden [1993b] identified mean vertical advection as the most important effect modifying linear Kelvin propagation. In sum, the intraseasonal Kelvin waves are reasonably well described and understood, particularly once they leave the generation region in the western Pacific. The present paper extends the existing description by connecting the waves to the Madden-Julian Oscillation (MJO) in the atmosphere and follows up Enfield's [1987] query by proposing an interaction between the intraseasonal and the interannual variability of the Pacific ocean-atmosphere system.
Intraseasonal variability in the tropical atmosphere has been the subject of
many papers since Madden
and Julian [1971, 1972]
used surface pressure and upper air data collected from stations around the
tropical belt to show that these fluctuations were of global scale and had aspects
suggesting an eastward-propagating wave. The convective signal associated with
the MJO has been studied using satellite-derived outgoing longwave radiation
(OLR) data and is found to be most prominent over the warm pool regions of the
eastern hemisphere (roughly between 60°E and 180°) [Rui
and Wang, 1990]. Eastward movement of convection is clearest during
boreal winter when the warm pool extends from the Indian Ocean to the date line
and lies closest to the equator [Weickmann
et al., 1985; Lau
and Chan, 1985, 1986;
Lau
and Shen, 1988]. Migration speeds are observed to range between
There has been considerable ambiguity in the literature about the exact meaning
of "intraseasonal," with many of the early atmospheric papers citing
periods in the range of
The widespread and systematic influence of ENSO on the ocean-atmosphere system
led to the initiation of the Tropical Ocean-Global Atmosphere (TOGA) program,
a 10-year study of climate variability on seasonal to interannual timescales.
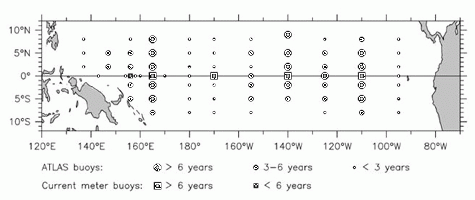
One component of the TOGA observing system is the Tropical Atmosphere Ocean
(TAO) buoy array, which consists of more than 60 deep ocean moorings arranged
in ranks nominally 15° longitude apart across the equatorial Pacific (Figure
1). Observations from these moorings form the principal data set used in
this paper. Most of the TOGA-TAO buoys are ATLAS thermistor chain moorings [Hayes
et al., 1991b] that measure temperature at the surface and 10 subsurface
depths down to 500 m, as well as surface winds, relative humidity, and air temperature.
Air temperatures, relative humidities, and water temperatures are sampled 6
times per hour, and daily averages of these are transmitted in real time each
day to shore by satellite via Service Argos. Vector winds
Figure 1. The TOGA-TAO buoy array as of September 1993, showing the approximate length of time the various buoys have been in the water. The present study uses principally the long-term thermistor chain buoys and the current meter buoys, which have been operating for 5 years or longer.
The most important advantage of the buoy data over shipboard observational
techniques is that their high temporal resolution means that intraseasonal frequencies
are not aliased by the ubiquitous high-frequency variability in the ocean [e.g.,
Hayes, 1982; Hayes
and McPhaden, 1992]. However, due to vandalism and instrument failures
of various types, the buoy time series are rarely complete, and some method
for dealing with data gaps is necessary. The history of instrumentation at the
0°, 140°W mooring is shown in Figure 2, indicating
that the time series at most depths are quite gappy and that the mix of samples
changed many times during the decade that a buoy has been in the water at this
location. These changes influence the choice of variables available for study.
For example, although dynamic height might be most useful for some purposes,
there are many periods during which there are no data below
For gaps that are short compared to the period of the signal of interest, it is possible to trade time resolution for gap filling. Chelton and Davis [1982, Appendix] show how to objectively estimate the value of a running mean in the presence of gaps. Their method has been used to fill small (up to about 10 days) gaps by producing a data series filtered with a 17-day triangle (two successive 9-day running means) filter. This filter has a half-power point at 20.3 days and so fills short gaps while retaining the intraseasonal signals of interest here.
The ability to low-pass filter in the presence of gaps also makes possible
the use of complex demodulation on the gappy buoy time series. Complex demodulation
[Bloomfield,
1976] is a type of band-pass filter that gives the time variation of the
amplitude and phase of a time series in a specified frequency band. It may be
preferable to ordinary Fourier techniques when studying a short or gappy record
since the result is local in the sense of being determined only by the data
in the neighborhood of each particular time realization. Briefly, in complex
demodulation the time series is first frequency-shifted by multiplication with
e-i 
t,
where is the central
frequency of interest. Then the shifted time series is low-pass filtered (using
the Chelton
and Davis [1982] method if there are gaps), which removes frequencies
not near the central frequency. This low pass acts as a band-pass filter when
the time series is reconstructed (unshifted). The resulting complex time series
can then be expressed as a time-varying amplitude and phase of the variability
in a band near the central frequency; that is, in the form t
-(
t)),(t)
the phase for a central frequency ,
and h(t) is the reconstructed band-passed time series. The phase
variation can also be thought of as a temporal compression or expansion of a
nearly sinusoidal time series, which is equivalent to a time variation of frequency.
While this study focuses on the 4-year period since mid 1989, there are two sites where
10-year time series of subsurface temperature and velocity have been collected, at 140°W
and 110°W on the equator. These allow examination of the extent to which the past 4 years
are typical of the climatology. Figure 2 shows the low-pass
filtered (half power at
Figure 2. Buoy sampling diagram at 0°, 140°W, showing the history of observations at this location at the various depths sampled. Note that only a few depths have continuous sampling over the 10 years of operation. The overlay of 20°C depth (filtered with a 121-day triangle (dark), and 17-day triangle (light)) shows that this value can be reliably calculated by vertical interpolation with no gaps even though temperature at any of the fixed levels would be gappy.
Pentad averages of twice-daily outgoing longwave radiation (OLR) data observed by satellite were used in this study to estimate the location and strength of tropical deep convection. This data set has been the basis for numerous studies of tropical convective activity, in which low values of OLR are assumed to indicate the presence of tall cumulus towers associated with intense convection [Weickmann et al., 1985; Lau and Chan, 1985; Rui and Wang, 1990; Waliser et al., 1993]. The data are obtained from National Oceanic and Atmospheric Administration's polar-orbiting satellites as radiance measurements in an infrared window channel. The window radiance is then converted to a broad-band estimate of the total outgoing longwave radiation [Gruber and Krueger, 1984]. Global measurements are binned into a day and a night observation on a 2½° by 2½° global grid. Missing data occur both in time and space. The data used here have been interpolated in time and then averaged into 73 pentads per year. Chelliah and Arkin [1992] have documented spurious variability in the OLR data due to different satellite equatorial crossing times and different window channel radiometers. These variations are confined to certain regions, especially those having a large diurnal cycle and should have no impact on our results.
The intraseasonal Kelvin waves are clearly seen as sloped bands of high and
low values in the longitude-time plot of 20°C depth along the equator (Figure
3). We show the 4-year period from mid 1989 to mid 1993 because there were
sufficient buoys to reliably perform the zonal interpolation and because the
waves were relatively well developed at this time. The previous
Figure 3. Longitude-time plot of 20°C depth on the equator. The contours and shading show the depth of the 20°C isotherm, zonally interpolated between the buoy positions (see text). Contour interval is 20 m, and deeper thermocline depths are darker shades. The slanted lines show identified downwelling Kelvin wave ray paths (see text) and represent a speed of 2.4 m s-1. The heavy line at top shows the time series of zonal winds averaged over 165°E-180° (scale at upper right). Both time series have been smoothed with a 17-day triangle filter (see text).
Observed changes to the mean thermocline slope and depth during the
It is clear from Figure 3 that the intraseasonal
Kelvin waves form a major component of equatorial thermocline depth variability.
Slanted lines have been overplotted to show the downwelling waves; their slope
represents a speed of 
= cT gives
There is a close visual coherence between zonal winds over the far western Pacific
(heavy line at the top of Figure 3) and thermocline depth
in the east/central Pacific. Figure 3 shows that virtually
every western Pacific wind fluctuation was reproduced in 20°C depth signals propagating
across the basin at Kelvin-like speeds of 2 to 3 m s-1. The correlation of
zonal winds at 165°E with 20°C depth at 140°W was greater than 0.7 at a lag of
The corresponding longitude-time plot of surface zonal winds along the equator (Figure 4) suggests that the zonal wind has a shorter zonal coherence scale than either 20°C depth or SST. Typically the strongest trades in the central Pacific occur during boreal fall/winter, which is when westerly events are most prominent in the far west. This out-of-phase relation between central and western Pacific is associated with the westward propagation of the annual cycle of zonal winds across the basin [e.g., Meyers, 1979; Lukas and Firing, 1985; Gent, 1985; Kessler and McCreary, 1993]. The result is that the correlation of winds along the equator has a relatively short zonal scale and becomes negative after a few thousand kilometers. The short zonal scales are consistent with those observed for deep tropical convection [Waliser et al., 1993].
Figure 4. Longitude-time plot of zonal winds on the equator. The plot has the same format as Figure 3 for 20°C depth. The contours and shading show the zonal wind at a contour interval of 3 m s-1. Westerlies are darker shades. The heavy curve at top show the time series of OLR averaged between 160°E and 170°E on the equator, with values below 220 W m-2 darkened (scale at upper right). Both time series have been smoothed with a 17-day triangle filter.
Western Pacific westerly winds often appear as a series of roughly month-long events,
rather than a simple annual sinusoid (Figure 4). Unlike
20°C depth (Figure 3) there is only weak evidence of
eastward propagation of the individual intraseasonal wind events, but successive events
often extend farther to the east than did the preceding one. The 1991-1992 El Niño is
evident in the zonal wind time series as a stronger-than-usual period of westerly events,
which extended further east than in the preceding years (Figure
4). This low-frequency signal was disrupted by the intraseasonal waves, and between
the strong westerly events the western Pacific winds returned to more normal conditions
with easterlies or very weak westerlies (Figure 4). With
the first of the series of MJOs in September 1991, substantial weakening of the trades
west of about 170°W was observed (Figure 4). The
"collapse of the trades" occurred during January 1992, when westerly winds were
seen as far east as 140°W for about
The occurrence of western Pacific westerly events corresponded closely to low values of
OLR, which indicate the presence of intense tropical convection (heavy line at the top of Figure 4). At 0°, 165°E, the largest lag correlation of
zonal winds and OLR was 0.7, with OLR leading the winds by about
The corresponding longitude-time plot of sea surface temperature (SST) along the
equator (Figure 5) shows a very different character of
variability. Whereas thermocline depth and western Pacific zonal winds demonstrated
large-amplitude intraseasonal fluctuations, SST variations were largely of lower
frequency. An annual cycle was prominent east of about 170°W, and in the eastern Pacific
the annual occurrence of warm SSTs lagged the deepest thermocline (Figure 3) by 2-3 months. During the ENSO warm event of
1991-1992 the 29°C isotherm moved east from its usual position near the date line to
about 140°W, and maximum SST at 110°W reached 28°C, about 1°-2°C warmer than the
annual maxima of the previous 2 years. Before the 1991-1992 event, in 1989 and 1990 the
cold tongue (defined roughly as the SST less than 25°C) persisted through January of the
following year east of 140°W. However, in September-October 1991 a relatively abrupt
warming took place across the basin, which roughly coincided with the first of the four
downwelling Kelvin waves of this event and terminated the annual cold period about 3
months earlier than usual (Figure 5). While the SST was
warming to its peak in the eastern Pacific during March 1992, the western Pacific at
165°E cooled below 29°C for the first time since 1989. Superimposed on these
low-frequency changes of SST in Figure 5 are 500-
Figure 5. Longitude-time plot of SST on the equator. The plot has the same format as Figures 3 and 4. The contours and shading show the SST (actually, the 1-m temperature) at a contour resolution of 1°C, with supplementary shading at 29.5°C. Darker shades show warmer SST. The slanted lines are the same Kelvin wave paths shown in Figure 3.
Spectra of OLR and zonal winds in the western Pacific, and 20°C depth and zonal
current at the undercurrent level in the central Pacific are shown in Figure
6. The spectra were calculated for the 10-year period April 1983-April 1993
for all quantities except the zonal wind, for which only the seven years July
1986-July 1993 are available. The spectra were estimated from the raw periodogram
amplitudes by smoothing in six frequency bands, with breaks at 600-, 225-, 110-,
45-, and 20-day periods, corresponding roughly to interannual, annual, semiannual,
intraseasonal, monthly and submonthly variability. Within each of these bands
the periodogram estimates were smoothed with a triangle filter whose length
was constant within the band; however, a longer filter length was used to give
greater smoothing in the higher-frequency bands. The resulting degrees of freedom
(DF) were estimated according to the procedure of Bloomfield
[1976, Chapter 8]; these range from 5 DF in the interannual band, to about
20 DF in the intraseasonal band and to about 60 DF for periods less than
Figure 6. Variance-preserving spectra of OLR at 165°E, zonal wind at 165°E, 20°C depth at 140°W, and equatorial undercurrent speed at 140°W, 120 m depth, all at the equator. Each variable has a separate scale as indicated. The spectra are calculated for the 10-year period April 1983-April 1993 for all quantities except the zonal wind, for which only the 7 years July 1986-July 1993 are available.
The spectra given in Figure 6 show that the intraseasonal band was a prominent feature of the variability of all these quantities, as expected from previous results and the plots discussed in section 3.1. The longitudes chosen for Figure 6 are roughly at the maximum amplitude of intraseasonal variability for OLR and 20°C depth; in the case of zonal wind this amplitude increased toward the west and may have been larger to the west of 165°E. The amplitude of zonal winds and OLR in this band dropped off rapidly east of the date line, so much of the oceanic intraseasonal variability in the eastern Pacific must have been remotely forced. The intraseasonal band variability in the atmospheric quantities shown (OLR and zonal wind) was skewed toward the high-frequency end of the band near 45-day or shorter periods, while the oceanic variability (20°C depth and undercurrent speed) peaked near 60- to 75-day or longer periods (Figure 6). There was little oceanic energy in the central Pacific at periods shorter than 50 days, even though there was such energy in OLR and the wind forcing. This discrepancy is reflected in the fact that many of the papers discussing intraseasonal variability in the atmosphere refer to "30-60 day" or "40-50 day" fluctuations [e.g., Madden and Julian, 1972; Weickmann et al., 1985; Lau and Chan, 1985, 1986; Zhu and Wang, 1993], but the ocean seems to selectively respond to the lower-frequency part of the intraseasonal forcing. We discuss this question further in section 4.6.
In addition to the intraseasonal peak, major spectral peaks are also seen at
3- to 4-year periods associated with the ENSO cycle, and at the annual period
(Figure 6). Weak semiannual variability was indicated
for all four quantities, with only slightly higher energy levels than neighboring
frequencies. It is noteworthy, but beyond the scope of this paper, that although
there have been large changes, even reversals, of the equatorial undercurrent
in the central Pacific associated with El Niño [e.g.,
Firing et al., 1983; Halpern,
1987], these events were short lived and did not compose a very large fraction
of the variance, so there was no interannual spectral peak of zonal current
at
All four quantities shown in Figure 6 were coherent at
periods longer than 1 or
Figure 7. Squared coherence amplitude of OLR at 165°E, zonal wind at 165°E and zonal current at 140°W with 20°C depth at 140°W; 95% confidence levels are indicated by the thin horizontal lines, which also show the frequency bands used to smooth the raw periodograms (see text).
The intraseasonal coherence among OLR, west Pacific winds and central Pacific
thermocline is not surprising, but it is important because the OLR events are
known to propagate eastward into the Pacific from the Indian Ocean as part of
the Madden-Julian Oscillation [Weickmann
et al., 1985; Rui
and Wang, 1990]. The Indian-Pacific connection is shown by high coherence
in the intraseasonal band between OLR at 90°E in the eastern Indian Ocean and
20°C depth at 140°W,
Figure 8. Squared coherence amplitude (top) and phase (bottom) of OLR at 90°E with 20°C depth at 140°W. The intraseasonal peak is centered at 74 days. Positive phase indicates deep 20°C depth leads low OLR. (Top) 95% confidence limits on the coherence amplitude are shown by the thin horizontal lines; 95% confidence limits on the phase are shown as "error bars," in each of the five frequency intervals in which the coherence (top panel) is significant above the 95% level. The phase limits are an average over each such interval and are plotted at the center of the intervals.
The Pacific Ocean Kelvin wave speed itself is found from Figure
9, which shows the squared coherence amplitude and phase of 20°C depth across
the equatorial band, averaged over periods of 55-
n(z) [Cane,
1984; Kessler
and McPhaden, 1995a]. When these quantities are calculated from the
mean historical profiles at different locations along the equator in the Pacific,
it is found that the first-mode speed c1 varies only from
about n(z)
show considerably more zonal variation, which might be expected to result in
wave reflections and interactions between modes [Gill
and King, 1985; Long
and Chang, 1990]. One can interpret the nearly constant phase speed
in a reduced gravity representation (where the phase speed is c2
= g(
/)H,
with
the density contrast across the interface and H the mean interface depth).
Although the thermocline shoals in the east, the vertical density contrast increases
in the cold tongue region, and the two compensate to produce a net change in
c that is less than would occur due to thermocline depth variations alone.
Figure 9. Squared coherence amplitude and phase of 20°C depth over the zonal extent of the buoy array with that at 140°W, averaged in the frequency band 55-65 days. The solid line shows the coherence amplitude (identically 1 at 140°W), and the light dashed horizontal line is the 95% confidence level (scale at left). The heavy dashed line is the phase, expressed as a lag in days with the phase at 140°W (scale at right). The thin solid line along the phase is a best fit straight line to the phase and represents a speed of 2.43 m s-1. This fit is the basis for the slope of the slant lines in Figures 3 and 5.
The spectral representations shown in Figures 6, 7, 8, and 9 depict the average variability over the whole record
lengths. Complex demodulation is a simple technique that gives time series of the
amplitude and phase of the variability within a frequency band (see section 2.1) and thus
allows examination of the temporal modulation of energy content of a particular band.
Demodulation of the time series of 20°C depth at 140°W, at a central period of
Figure 10. Time-varying amplitude of the intraseasonal variability obtained through complex demodulation of (a) 20°C depth at 0°, 140°W, (b) zonal winds at 165°E, and (c) OLR at 165°E. The demodulation is performed about a central frequency of 60 days, with half-power between 42 and 108 days. The dashed line overlaid is a 1-year running mean of each demodulated time series.
Figure 11. Average year of 60-day amplitude of 20°C depth at 0°, 140°W (meters, solid line, scale at left; data from Figure 10a), zonal winds at 165°E (meters per second, dashed line, scale at right; data from Figure 10b) and OLR at 165°E (W m-2, dotted line, scale at left; data from Figure 10c).
In late 1988 a sharp peak of 60-day amplitude occurred that did not represent the usual annual downwelling Kelvin waves associated with MJO convection and westerlies in the western Pacific, despite the fact that it appears to fit the annual pattern of maxima (Figure 10a). Instead, this event was a strong upwelling signal that was generated by a fairly confined patch of easterly winds near the date line [Picaut and Delcroix, 1995] and marked the maximum cooling of the La Niña of 1988 (Figure 2). If we omit the non-MJO 1988 peak, the largest intraseasonal signals of 20°C depth are found at the beginnings of 1987 and 1992 (Figure 10a), both associated with the El Niño events of those years, and these appear as enhancements of the deep-thermocline phase of the annual cycle.
The corresponding demodulation of zonal wind at 165°E is shown in Figure
10b. As in the case of 20°C depth, a strong annual signal of 60-day variability
is seen, with peaks roughly 3 times larger than the background occurring at
the end of each year. The average annual and semiannual variation of 60-day
wind amplitude (Figure 11) is very similar to
that for 20°C depth, with the western Pacific winds leading 140°W 20°C depth
by
The corresponding demodulation of the OLR time history averaged over 160°-170°E on
the equator is shown in Figure 10c. Again, for most years
the OLR intraseasonal variability peaked in boreal fall/winter with an amplitude 2 to 3
times the background. The average year of OLR 60-day amplitude (Figure
11) shows peak amplitude in February-March,
We have shown that the commonly observed intraseasonal Kelvin waves in the equatorial Pacific are generated by the fluctuations of winds and tropical convection associated with the MJO. In particular, the waves exhibit low-frequency modulation due to annual and interannual variations of west Pacific convection, which itself is a signal propagating from further west. Since the MJO life cycle is sensitive to the distribution of warmest SST over both the Indian and Pacific Oceans, and to the planetary atmospheric circulation, the oceanic signal must be taken to be a manifestation of a global phenomenon, and not simply internal to the Pacific. Although it is easy to see how low-frequency variations of SST in the Pacific can affect the MJO, which has its intense convection signals over the warmest SST, we now ask whether the MJO events themselves could have a role in the interannual variations of the Pacific. Such a process would require a nonlinear coupling between the relatively high intraseasonal frequencies and a rectified low-frequency response.
One mechanism that might produce this interaction is suggested by the 500- to 1000-km intraseasonal bumps on the SST contours in Figure 5, which occur both in the eastern and western Pacific. SST variability at this timescale, in the absence of corresponding atmospheric forcing, points to zonal advection by the intraseasonal Kelvin waves as a possible explanation. In view of the fact that convection and westerly winds follow the warmest water eastward, this could provide a mechanism by which intraseasonal variability in the ocean can feed back to affect the atmosphere. Since the atmosphere can respond to SST forcing (by shifting the location of convection) much more rapidly than the ocean responds to changing winds, each eastward advection event can draw subsequent convection further east.
An apparent example of this process occurred during the basin-wide warming
of the El Niño of 1991-1992. Figure 12a shows
a detail of the SST zonal section from Figure 5
for the period July 1991 through April 1992. Overlaid on the SST contours and
shading are, first, the zero contour of the zonal winds (same data as Figure
4) showing the advance-and-retreat eastward expansion of westerlies, and
second, the Kelvin wave propagation lines from Figure
3 showing the four downwelling waves (associated with eastward current anomalies)
observed in 20°C depth during the onset of the 1991-1992 warm event. The second
and third westerly events, in November 1991 and January 1992, each extended
about
Figure 12. (a) Detail of SST on the equator for July 1991 through April 1992 (during the peak of the El Niño of 1991-1992). Contours and shading show SST with a contour interval of 1°C, with supplemental contour/shade at 29.5°C. Light contours show warmer temperatures (opposite of Figure 5). The heavy slant lines are the same Kelvin lines shown in Figure 3. The heavy contour labeled "0" is the zero line of zonal winds, showing the steplike progression of westerlies eastward over the Pacific during the onset of the warm event. (b) Model SST/wind to match the timing of Figure 12a. Output of the simple model described in section 4. The heavy curve is the eastern edge of the 29°C SST and the wind patch (the result of integrating (3); see text). The light sinusoidal curve at top is the time series of winds from (1) (up is easterly, down is westerly) (winds are zero before day 0). The shading shows the region of westerly winds. Slant lines indicate maximum positive pressure perturbation to match the observed Kelvin lines in Figure 12a; east of the forced region these are Kelvin characteristics, within the forced region they move at speed 2c (see text).
Kessler and McPhaden [1995b] studied the zonal advective effect on SST at 140°W during the 1991-1993 El Niño and showed that although this forcing was not the most important term in the SST balance at annual and interannual frequencies it was dominant during the period of intense intraseasonal variability at the height of the warm event. Figure 13 compares the advective terms d(SST)/dt and ud(SST)/dx at 0°, 140°W (d(SST)/dx is estimated by centered difference between 155°W and 125°W) during the same period as Figure 12a for SST and winds. The positive (warming) humps of -ud(SST)/dx in Figure 13 show the advection due to the intraseasonal Kelvin waves at 140°W in October and November-December 1991 and January 1992. Clearly, the first major warming that took place in September was not the result of Kelvin advection, but the next two events are quite consistent with that interpretation, and the two terms balance closely. The final warming in March occurred before the passage of the fourth Kelvin wave and again was apparently not due to that wave. The fourth wave produced only a very weak advective signal in Figure 13 because the zonal temperature gradient at 140°W was near zero at that time (Figure 12a).
The net result of successive intraseasonal waves associated with steplike eastward
movement of the warmest water and westerly winds appears as a much lower-frequency
signal. In this view, Figure 12a suggests that
zonal advection moved the 29.5°C water
Figure 13. Comparison of d(SST)/dt and ud(SST)/dx at 0°, 140°W. The solid line shows -ud(SST)/dx, where u is taken as the 14-m (shallowest level) zonal current measured by ADCP and d(SST)/dx is estimated by centered difference between 125°W and 155°W. The dashed line is d(SST)/dt at 140°W. Both time series are filtered with a 17-day triangle filter. Upward on the plot indicates a warming tendency for both time series.
A simple coupled model illustrates the dynamics involved. The model is not intended to be a realistic simulation of all or even most aspects of the onset of El Niño, but simply to show that a nonlinear interaction between the oceanic intraseasonal Kelvin waves and the Madden-Julian Oscillation is possible. The model is highly idealized to represent the single mechanism of an advective feedback between intraseasonal advection of SST and the rapid response of the atmosphere to changes of location of the warm pool. This feedback may be an element of the slow eastward advance of warm SST and atmospheric convection that has been noted to occur during the onset of warm events.
Assume that the initial state of the ocean has a warm pool extending eastward from the western boundary. Let sinusoidally oscillating, zero-mean zonal winds occur only to the west of a particular value of SST, say the 29°C isotherm. The frequency and phase of the surface winds is assumed to be fixed by upper atmosphere waves oscillating at a Madden-Julian timescale, but their longitudinal extent is determined by the SST. For simplicity, we assume that the winds do not vary in longitude within the wind patch (from the western boundary to the 29°C SST isotherm), but are zero outside the patch. In the ocean, Kelvin waves forced by the oscillating winds advect the 29°C patch edge. We assume a simple ocean dynamics such that the ocean response to winds is that the forced ocean current is directly proportional to the wind integrated over the Kelvin wave characteristic. Other than zonal advection, due to Kelvin wave passage or to wind forcing directly, there are no processes that affect SST in this model.
This model can be formulated as follows. The western boundary is at x = 0. Let x = a(t) mark the (time varying) east edge of the 29°C SST/wind patch. Then the wind field is
(1)
where b is the (constant) amplitude of the wind and the frequency. Note that uatmos has zero
mean. The ocean current at the patch edge is now taken to be directly proportional to the
wind integrated over the patch along the Kelvin wave characteristic. The integral sums the
forcing felt by a wave since it left the western boundary.
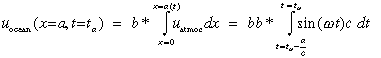(2)
where b* is the (constant) coupling efficiency, c is the
Kelvin wave speed, and ta is the arrival time of Kelvin characteristics
at the patch edge. The coupling efficiency b* scales the speed of the
current generated by a given wind, and is a tunable parameter in this model. For
simplicity of notation, we combine bb* = B, which has units of
(time)-1 and incorporates the effects of both wind strength and coupling
efficiency; thus B represents the net forcing amplitude felt by the ocean. Since
the wind does not vary (in x) for 0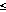 
x 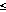a(t), the integration can be performed in time
alone from t = ta - a/c (the time a characteristic
leaves x = 0) to t = ta, as indicated in (2). Since the
patch edge position a(t) is changed only by zonal advection, we identify uocean
= da/dt = rate of change of position of the patch edge. Carrying out the
integral in (2),
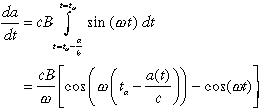(3)
This is a nonlinear (because a(t) appears in the argument to
the cosine on the right-hand side) ordinary differential equation, which can
be easily integrated numerically. We see from (3) that da/dt is
zero for a = 0 (no patch) or for a = 2
c/
(a patch with width the same as the wavelength of a Kelvin wave of frequency
), so these are limiting
equilibrium positions where the motion stops, but the motion can be of either
sign between these two locations.
Reasonable values of the model parameters can be chosen as follows. We have
established that the Kelvin wave speed is c =
= 2/(60 days). The wind
forcing amplitude B can be estimated from the wind-forced linear zonal
momentum equation
(4)
where 
= acDua2
(subscripts a and o here indicate atmosphere and ocean, respectively, and cD
is the drag coefficient), and H is the thickness of the wind-forced layer. Taking
usual values a = o =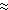
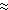
Note that the estimate of the tunable parameter B from (4) is proportional to
the wind speed squared and also that the choice of the wind-driven layer depth is somewhat
arbitrary. In any case, the model has a simple parameter space, and the response is
qualitatively the same for all values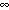 
.c/ (and note that the
equilibrium value is not a function of the wind forcing parameter B, but only of
the unambiguous quantities c and ). For
(unrealistically) large values of B the solution can jump to an integer multiple of
2c/ but then resumes
identical behavior approaching the new equilibrium position. The model is also not
sensitive to the starting phase of the wind. In the example discussed in section 4.3 and
shown in Figure 12b we have started the winds at the
beginning of their westerly phase at time zero (winds are zero before t = 0), but
if the winds are started easterly at t = 0, the process takes several more
oscillations before rapid growth occurs, but the eventual result is the same.
The behavior of the solution is shown in Figure
12b. The patch edge moves east in pulses not dissimilar to those observed
(Figure 12a) for SST and westerly winds during
late 1991. Each step advances about 1000-c/
(in the present example 2c/
=
The solution has a basic similarity to the results of a coupled general circulation model simulation reported by Latif et al. [1988]. They added a single 30-day westerly wind event to their model after spin up with annual cycle forcing and then let the coupled system run freely. The model responded with an initial rapid eastward shift of the SST maximum toward the central Pacific due to zonal Kelvin wave advection, then subsequently the model atmosphere developed persistent westerlies blowing toward the warmest water. This kept the central basin sea level and SST high for at least a full year after the single 30-day imposed forcing event. Although the Latif et al. [1988] model is much more complex than the present formulation, it appears that the coupled dynamics are similar in this case, with the atmosphere responding to transient eastward displacement of warm SST by developing westerlies that serve to maintain and extend the SST pattern.
The key dynamics that produce the rectified low-frequency outcome from the high-frequency forcing is that the model atmosphere responds immediately to the state of the SST, while the ocean's response to the atmosphere is lagged because it is due to an integration over forcing of finite duration. While the model is crude, this timescale difference between the two fluids is probably representative of a true distinction. The other important characteristic of the model formulation is that the strength of the model ocean response is proportional to the fetch, so that westerly winds, which advect the patch edge eastward, increase the fetch, while easterly winds reduce it. Thus during westerly periods the increasing fetch means the response increases, but during easterly periods the decreasing fetch produces a weaker signal, so each westward retreat is somewhat weaker than the eastward advances. This behavior is much like the observations in late 1991.
We noted in the introduction that the Madden-Julian Oscillation is a global phenomenon, but its surface expression is strong only over the warm-SST part of the equatorial ocean. Similarly in the model, we assume that the forces that establish the basic oscillation are entirely external to the feedback mechanism. In this representation the atmospheric dynamics of the MJO set the 60-day oscillation period, while the SST determines only the zonal length of the region in which convection and strong low-level winds develop during the phase favorable to upper-level divergence. Although the existence of the MJO probably requires a minimum size warm SST region to exist, the few-thousand-kilometer changes during a single event may be small perturbations to the global state SST felt by the atmosphere, and thus the interaction described here may not strongly affect the fundamental dynamics or frequency.
Several important weaknesses of the model are evident. We neglect entirely
any heat exchange between the atmosphere and ocean, which is obviously crucial
to the evolution of the coupled system. The present, highly-idealized formulation
can only be relevant over short time scales during which the rapid advection
that occurs as a result of the intraseasonal waves can be the dominant process
affecting SST. Such dominance of intraseasonal Kelvin wave-mediated zonal advection
on SST change can occur during warm event onset and was observed at 140°W during
November 1991 through February 1992 (section 4.1 and Figure
13). Second, the model implicitly has an infinite heat reservoir that allows
the warm pool to expand indefinitely, determined only by dynamics, not a heat
balance. However, the same result would still occur if eastward advection in
the warm pool exposed cooler water to the west, if one makes the reasonable
assumption that the convection and westerlies advance over the cool water to
the warm pool. Similarly, SST cooling due to evaporation associated with the
increase in absolute wind speeds during westerly events in the western Pacific
is typically less than 1°C, which is not enough to reduce the absolute temperature
to below the threshold needed for deep convection. Therefore the primary feedback
shown by the simple dynamics would not change if the model was made more realistic
by allowing changing SST under the winds. However, such cooling may well have
been the reason for the slight decrease in warm pool SST under the strong winds
of January 1992 (Figure 12a). Third, in order
to demonstrate without ambiguity that the slow change in the ocean can be due
entirely to the coupled feedback rectification, we have postulated zero mean
wind forcing. In the real event, it is observed that the onset of El Niño occurs
in a regime of low-frequency westerly forcing with the higher-frequency convection
events superimposed (Figure 3, top). This would
tend to make the eastward advective signal stronger, but the aim here is to
show that it is not necessary to have mean westerly forcing in order to get
a net eastward propagation in the ocean. Fourth, to achieve maximum mathematical
simplicity, we have specified that the winds do not vary in x within
the wind patch (equation (1)). In fact, the wind signal propagates eastward
with the convection signal at speeds of the order of
An element of the ocean dynamics that we have ignored is the Rossby waves that
would also be generated by the oscillating forcing. Rossby waves might affect
the result in three ways. First, the Kelvin waves discussed here would produce
Rossby waves upon reflection at the eastern boundary. However, a variety of
studies [du
Penhoat et al., 1992; Kessler
and McCreary, 1993; Kessler
and McPhaden, 1995a; Minobe and Takeuchi (Annual period equatorial waves
in the Pacific Ocean, submitted to Journal of Geophysical Research, 1994))
have suggested that these waves will not survive propagation across the entire
Pacific, thus we think this would not be a major element of a more complete
solution. Second, the oscillating winds would generate Rossby waves directly.
These waves propagate west, and so would not influence the east edge of the
patch, except by producing secondary Kelvin waves upon reflection from the western
boundary. The amplitude of the Rossby waves forced by the wind patch depends
on the meridional shape of the wind field; the amplitude of the consequent reflected
Kelvin waves depends on the mix of Rossby meridional wavenumbers and the shape
of the western boundary [Clarke,
1983; McCalpin,
1987; Kessler,
1991]. The phase of the resulting Kelvin waves depends on the zonal width
of the patch, and we can anticipate that as the patch length changes the Kelvin
waves due to boundary reflection will exhibit varying phase compared to the
directly forced waves and may be of either sign relative to the original solution.
The time lag for Rossby wave propagation from the patch edge to the western
boundary and then Kelvin wave propagation back to the patch edge a can
be written tR =
A third way in which our neglect of Rossby waves in the model is unrealistic is that
there can also be easterly wind anomalies to the east of the convection on MJO timescales,
and these would generate Rossby waves carrying equatorial currents westward toward the
patch edge that would oppose the Kelvin signals modeled here. It is not straightforward to
model these Rossby waves in the context of a model as simple as the present one, since the
zonal width of the easterly forcing is much harder to define than the width of the
convective region. Also note that the much slower Rossby propagation speed (1/3 of the
Kelvin speed for first-meridional-mode waves) implies that a reasonably sized easterly
patch region of c/, and the
integral over the characteristic would thus be small (see discussion of equation (6) and Figure 14 in section 4.6). In addition, we have noted that the
central Pacific intraseasonal zonal wind variability is very much weaker than that over
the warm pool (see Figure 4). In sum, we conclude that our
neglect of the Rossby wave forcing, while unrealistic, does not distort the fundamental
feedback properties of the model.
Figure 14. Complex (frequency domain) EOF 1 of intraseasonal (30- to 80-day period) OLR along the equator in the Pacific during 1979-1993. (Top) Amplitude (W m-2) of the complex eigenvector. The zonal structure of this EOF is used to estimate the zonal length of the OLR patch (see text). (Middle) Phase relative to 125°E. The slope in the western Pacific indicates eastward propagation at a speed of about 4.5 m s-1. (Bottom) Percent variance represented.
Recognizing that all these dynamic and thermodynamic weaknesses and crude approximations to the observations make the model unsuitable for realistic simulation of the coupled system in general, the extremely simple form used here was chosen for the purpose of isolating a particular process that may be relevant to the real system during a limited (but perhaps important) period.
We have shown (in agreement with previous studies) that although intraseasonal
variability in the atmosphere was centered at 35- to 60-day periods (Figure 6), the ocean response was shifted toward the
lower-frequency end of the band. Thermocline depth and undercurrent speed variability were
very weak at periods less than c/). For the 60-day waves
discussed above, this distance is
Using terminology analogous to the model (1)-(3), but with the patch edge fixed (no feedback), let A be the (fixed) east edge of the warm SST/wind patch. The wind field is still described by (1), substituting the constant A for the previously variable a(t). Performing the same integration as in (2), again substituting A for a(t), gives an equation analogous to (3) for the zonal current at the east edge A. Since A is fixed, this expression for u(x = A) may be written as the product of a constant amplitude and a time-varying term.
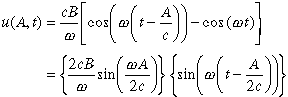(5)
where the first term on the right-hand side is the (constant) amplitude and the second is the time-varying term. The variance of the Kelvin response at A (and thus everywhere east of A) is the amplitude squared
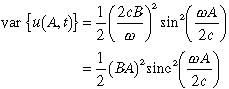(6)
where the function sinc(x) 
[x-1 sin(x)],
which equals 1 at x = 0, equals 0 at x = , and
thereafter represents a decaying oscillation for increasing values of x. In (6) the
variance falls to zero as the period decreases toward the value A/c (the
time it takes a Kelvin wave to cross the patch), because then, in summing the integral
over the wind patch, the easterly and westerly contributions to the ocean forcing cancel.
Therefore the amplitude of the ocean response east of equatorial wind forcing depends on
the product A, and for some values of these
parameters the response can vanish.
An estimate of the zonal length scale of the intraseasonal forcing can be made
using OLR, which spans the entire western Pacific (the buoy observations are
not suitable for this purpose since long records are available only east of
165°E). The 1979-1993 history of equatorial OLR was decomposed in complex empirical
orthogonal functions (CEOFs) in the frequency domain [Wallace
and Dickinson, 1972], using frequencies spanning 30- to 80-day periods
to define the intraseasonal band. Figure 14 shows
the amplitude, phase relative to 125°E and percent variance represented by the
first CEOF, as a function of longitude in the Pacific. In the western Pacific,
the first CEOF expresses 50% or more of the intraseasonal variance, with amplitudes
up to
Figure 15 shows the theoretical variance of zonal
current east of a 5000-km patch as a function of frequency, calculated according to (6),
using the Kelvin wave speed
Figure 15. Theoretical variance of zonal current east of a 5000-km width wind patch, calculated according to (6), shown as a function of forcing frequency. The top axis numbering shows the periods in days. Note the rapid drop in variance between 100-day and 30-day periods.
We have used 10-year time series of SST, 20°C depth, and zonal winds measured by moored buoys across the equatorial Pacific to define the intraseasonal Kelvin waves and compare them to an index of tropical convection. Previous studies have described and diagnosed the oceanic Kelvin waves; here we establish that the low-frequency modulation of the intraseasonal energy in the ocean coincides with that of the Madden-Julian Oscillation, and hence this signal should be seen as part of a planetary-scale phenomenon, and not internal to the Pacific. During the boreal fall/winter season, typically two to four intraseasonal convection events propagate into the western Pacific from their generation region over the central Indian Ocean. Westerly winds associated with the convection generate downwelling first-baroclinic-mode Kelvin waves that efficiently carry the signal across the basin; this composes a substantial fraction of eastern Pacific thermocline depth variability. During El Niño onset years (1986 and 1991 in this study), the convection extends further east (in association with the warmest SST), which gives more fetch to the westerlies and thus unusually intense downwelling Kelvin events.
A simple model is formulated that shows that a coupled feedback is possible in which intraseasonal wind forcing alone results in a slow, steplike eastward progression of high SST and westerly wind anomalies across much of the Pacific in a manner not unlike the onset stage of El Niño. The model is highly idealized, isolating a single process: the feedback between intraseasonal Kelvin wave zonal advection of SST interacting with eastward penetration of convection over the Pacific. The model solution implies that low-frequency modulation of the intraseasonal variability could lead to low-frequency climate fluctuations in the Pacific. Some of this modulation can presumably be due to changes in the Indian Ocean and south Asian monsoon circulation systems, so the intraseasonal band may be a "window" through which the Pacific reacts to signals originating outside the basin, and this may be part of the process that occurs during the onset stage of El Niño. We note, however, that intraseasonal equatorial Kelvin waves are a ubiquitous feature of the equatorial Pacific, evident during non-El Niño years as well. Thus the occurrence of these waves alone is not a sufficient condition for the onset of El Niño. A further application of the simple model suggests that the discrepancy between the typical 30- to 50-day periods of the most energetic atmospheric intraseasonal variability and the 60- to 75-day periods of the corresponding signal in the ocean may occur because of the correspondence between the relatively short periods of the intraseasonal wind and the time for a Kelvin wave to cross the wind patches.
It is presently a subject of controversy as to whether high-frequency variability such as the intraseasonal band is important to resolve, or whether it is enough to simply work with low-frequency averages, when the desired result is understanding of interannual variability [e.g., Latif et al., 1988; Zebiak, 1989; Webster and Lukas, 1992]. Our results suggest an intimate connection between large-amplitude intraseasonal waves and the onset of El Niño and raise the possibility that the waves themselves provide a feedback to the atmosphere that could be crucial to the spreading of the coupled anomalies across the Pacific.
Acknowledgments. The existence of the TOGA/TAO buoy array is due in large part to the vision and perseverance of the late Stanley P. Hayes. Without his efforts this study would not have been possible. We thank Nick Graham and Bob Weisberg for thorough reviews of an earlier version of the manuscript and many helpful comments and suggestions. We thank Eric Johnson for the use of his computer program to find the complex EOFs shown in Figure 14 and for discussions that helped clarify some of our ideas on statistical estimators. Marguerite McCarty expertly performed some of the computations. Support from the Equatorial Pacific Ocean Climate Studies (EPOCS) Program is gratefully acknowledged. This is NOAA PMEL contribution 1565.
Bloomfield, P., Fourier Decomposition of Time Series: An Introduction, 258 pp., John Wiley, New York, 1976.
Cane, M. A., Modeling sea level during El Niño, J. Phys. Oceanogr., 14, 1864-1874, 1984.
Chelliah, M., and P. Arkin, Large-scale interannual variability of monthly outgoing longwave radiation anomalies over the global tropics, J. Clim., 5, 371-389, 1992.
Chelton, D. B., and R. E. Davis, Monthly mean sea level variability along the west coast of North America, J. Phys. Oceanogr., 12, 757-784, 1982.
Clarke, A. J., The reflection of equatorial waves from oceanic boundaries, J. Phys. Oceanogr., 13, 1193-1207, 1983.
duPenhoat, Y., T. Delcroix, and J. Picaut, Interpretation of Kelvin/Rossby waves in the equatorial Pacific from model-GEOSAT data intercomparison during the 1986-1987 El Niño, Oceanol. Acta, 15, 545-554, 1992.
Enfield, D. B., The intraseasonal oscillation in eastern Pacific sea levels: How is it forced? J. Phys. Oceanogr., 17, 1860-1876, 1987.
Firing, E., R. Lukas, J. Sadler, and K. Wyrtki, Equatorial undercurrent disappears during 1982-83 El Niño, Science, 222, 1121-1123, 1983.
Gent, P. R., The annual cycle in the central equatorial Pacific Ocean, J. Mar. Res., 43, 743-759, 1985.
Gill, A. E., and B. A. King, The effect of a shoaling thermocline on equatorially-trapped Kelvin waves, Dynamical Climatology Technical Note 27, 28 pp., Meteorological Office, Bracknell, Berkshire, UK, 1985.
Gruber, A., and A. F. Krueger, The status of the NOAA outgoing longwave radiation data set, Bull. Amer. Meteorol. Soc., 65, 958-962, 1984.
Halpern, D., Observations of annual and El Niño thermal and flow variations at 0°, 110°W and 0°, 95°W during 1980-1985, J. Geophys. Res., 92, 8197-8212, 1987.
Hayes, S. P., A comparison of geostrophic and measured velocities in the Equatorial Undercurrent, J. Mar. Res., 40, Supplement, 219-229, 1982.
Hayes, S. P., and M. J. McPhaden, Temporal sampling requirements for low frequency temperature variability in the eastern equatorial Pacific Ocean, NOAA Tech. Memo., ERL-PMEL-96, 1992.
Hayes, S. P., P. Ripa, and L. J. Mangum, On resolving vertical modes with observational data, J. Geophys. Res., 90, 7227-7234, 1985.
Hayes, S. P., P. Chang, and M. J. McPhaden, Variability of the sea surface temperature in the eastern equatorial Pacific during 1986-88, J. Geophys. Res., 96, 10,553-10,566, 1991a.
Hayes, S. P., L. J. Mangum, J. Picaut, A. Sumi, and K. Takeuchi, TOGA/TAO: A moored array for real-time measurements in the tropical Pacific Ocean, Bull. Am. Meteorol. Soc., 72, 339-347, 1991b.
Hendon, H. H., and M. L. Salby, The life cycle of the Madden-Julian Oscillation, J. Atmos. Sci., 51, 2225-2237, 1995.
Johnson, E. S., and M. J. McPhaden, Structure of intraseasonal Kelvin waves in the equatorial Pacific Ocean, J. Phys. Oceanogr., 23, 608-625, 1993a.
Johnson, E. S., and M. J. McPhaden, Effects of a three-dimensional mean flow on intraseasonal Kelvin waves in the equatorial Pacific Ocean, J. Geophys. Res., 98, 10,185-10,194, 1993b.
Kessler, W. S., Can reflected extra-equatorial Rossby waves drive ENSO?, J. Phys. Oceanogr., 21, 444-452, 1991.
Kessler, W. S., and J. P. McCreary, The annual wind-driven Rossby wave in the sub-thermocline equatorial Pacific, J. Phys. Oceanogr., 23, 1192-1207, 1993.
Kessler, W. S., and M. J. McPhaden, Oceanic equatorial waves and the dynamics of the 1991-93 El Niño, J. Clim., in press, 1995a.
Kessler, W. S., and M. J. McPhaden, The 1991-93 El Niño in the central Pacific, Deep Sea Res., in press, 1995b.
Knutson, T. R., and K. M. Weickmann, 30-60 day atmospheric oscillations: Composite life cycles of convection and circulation anomalies, Mon. Weather Rev., 115, 1407-1436, 1987.
Knutson, T. R., K. M. Weickmann, and J. E. Kutzbach, Global-scale intraseasonal oscillation of outgoing longwave radiation during northern hemisphere summer, Mon. Weather Rev., 114, 605-623, 1986.
Latif, M., J. Biercamp, and H. von Storch, The response of a coupled ocean-atmosphere general circulation model to wind bursts, J. Atmos. Sci., 45, 964-979, 1988.
Lau, K. M., and P. H. Chan, Aspects of the 40-50 day oscillation during northern winter as inferred from outgoing longwave radiation, Mon. Weather Rev., 113, 1889-1909, 1985.
Lau, K. M., and P. H. Chan, Aspects of the 40-50 day oscillation during northern summer as inferred from outgoing longwave radiation, Mon. Weather Rev., 114, 1354-1367, 1986.
Lau, K. M., and S. Shen, On the dynamics of intraseasonal oscillations and ENSO, J. Atmos. Sci., 45, 1781-1797, 1988.
Long, B., and P. Chang, Propagation of an equatorial Kelvin wave in a varying thermocline, J. Phys. Oceanogr., 20, 1826-1841, 1990.
Lukas, R., and E. Firing, The annual Rossby wave in the central equatorial Pacific ocean, J. Phys. Oceanogr., 11, 55-67, 1985.
Madden, R. A., and P. R. Julian, Detection of a 40-50 day oscillation in the zonal wind in the tropical Pacific, J. Atmos. Sci., 28, 702-708, 1971.
Madden, R. A., and P. R. Julian, Description of global-scale circulation cells in the tropics with a 40-50 day period, J. Atmos. Sci., 29, 1109-1123, 1972.
McCalpin, J. D., A note on the reflection of low-frequency equatorial Rossby waves from realistic western boundaries, J. Phys. Oceanogr., 17, 1944-1977, 1987.
McCreary, J. P., and R. Lukas, The response of the equatorial ocean to a moving wind field, J. Geophys. Res., 91, 11,691-11,705, 1986.
McPhaden, M. J., Variability in the central equatorial Indian Ocean, I, Ocean dynamics, J. Mar. Res., 40, 157-176, 1982.
McPhaden, M. J., TOGA-TAO and the 1991-93 El Niño-Southern Oscillation event, Oceanography, 6, 36-44, 1993.
McPhaden, M. J., and S. P. Hayes, Variability in the eastern equatorial Pacific Ocean during 1986-88, J. Geophys. Res., 95, 13,195-13,208, 1990.
McPhaden, M. J., H. B. Milburn, A. I. Nakamura, and A. J. Shepherd, PROTEUS--Profile telemetry of upper ocean currents, in Proceedings of MTS '90 Conference, pp. 353-357, Marine Technology Society, Washington, D.C., 1990.
McPhaden, M. J., and M. J. McCarty, Mean seasonal cycles and interannual variations at 0°, 110°W and 0°, 140°W during 1980-1991, NOAA Data Rep., ERL PMEL-95, 118 pp., 1992.
McPhaden, M. J., and B. A. Taft, Dynamics of seasonal and intraseasonal variability in the eastern equatorial Pacific, J. Phys. Oceanogr., 18, 1713-1732, 1988.
Meyers, G., Annual variation in the slope of the 14°C isotherm along the equator in the Pacific Ocean, J. Phys. Oceanogr., 9, 885-891, 1979.
Nakazawa, T., Tropical cloud clusters within the intraseasonal variations over the western Pacific, J. Meteorol. Soc. Jpn., 66, 823-839, 1988.
Philander, S. G. H., and R. C. Pacanowski, Response of equatorial oceans to periodic forcing, J. Geophys. Res., 86, 1903-1916, 1981.
Picaut, J., and T. Delcroix, Equatorial wave sequence associated with warm pool displacements during the 1986-1989 El Niño-La Niña, J. Geophys. Res., in press, 1995.
Reynolds, R. W., and T. M. Smith, Improved sea surface temperature analyses using optimum interpolation, J. Clim., 5, 929-948, 1994.
Rui, H., and B. Wang, Development characteristics and dynamic structure of tropical intraseasonal convection anomalies, J. Atmos. Sci., 47, 357-379, 1990.
Spillane, M. C., D. B. Enfield, and J. S. Allen, Intraseasonal oscillations in sea level along the west coast of the Americas, J. Phys. Oceanogr., 17, 313-325, 1987.
Sui, C.-H., and K. M. Lau, Origin of low-frequency (intraseasonal) oscillations in the tropical atmosphere, II, Effect of an improved treatment of moist processes, J. Atmos. Sci., 46, 37-56, 1989.
Tang, T. Y., and R. H. Weisberg, On the equatorial Pacific response to the 1982/1983 El Niño-Southern Oscillation event, J. Mar. Res., 42, 809-829, 1984.
Wallace, J. M., and R. E. Dickinson, Empirical orthogonal representation of time series in the frequency domain, I, Theoretical considerations, J. Appl. Meteorol., 11, 887-892, 1972.
Waliser, D. E., N. E. Graham, and C. Gautier, Comparison of highly reflective cloud and outgoing longwave radiation datasets for use in estimating tropical deep convection, J. Clim., 6, 331-353, 1993.
Webster, P. J., and R. Lukas, TOGA-COARE: The coupled ocean-atmosphere response experiment, Bull. Am. Meteorol. Soc., 73, 1377-1416, 1992.
Weickmann, K. M., and S. J. S. Khalsa, The shift of convection from the Indian Ocean to the western Pacific Ocean during a 30-60 day oscillation, Mon. Weather Rev., 118, 964-978, 1990.
Weickmann, K. M., G. R. Lussky, and J. E. Kutzbach, Intraseasonal (30-60 day) fluctuations of outgoing longwave radiation and 250 mb streamfunction during northern winter, Mon. Weather Rev., 113, 941-961, 1985.
Weisberg, R. H., and T. Y. Tang, Equatorial ocean response to growing and moving wind systems with application to the Atlantic, J. Mar. Res., 41, 461-486, 1983.
Zebiak, S., On the 30-60 day oscillation and the prediction of El Niño, J. Clim., 2, 1381-1387, 1989.
Zhu, B., and B. Wang, The 30-60 day convection seesaw between the tropical Indian and western Pacific Oceans, J. Atmos. Sci., 50, 184-199, 1993.
Return to Abstract