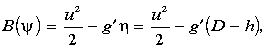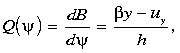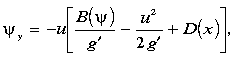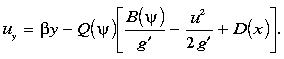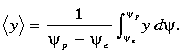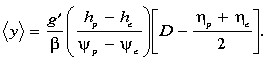The Tsuchiya jets, or subsurface countercurrents, extend across the Pacific Ocean carrying 7 (± 2) × 106 m3 s-1 eastward on each side of the equator. Mean meridional sections of potential temperature, salinity, neutral density anomaly, and the square of buoyancy frequency are presented for the western, central, and eastern tropical Pacific Ocean. These sections are used together with maps of depth and salinity on isopycnals, as well as thickness between isopycnals, to describe the evolution of the Tsuchiya jets as they flow from west to east. An inertial-jet model is formulated in which conservation of the Bernoulli function and potential vorticity combine with the eastward shoaling of the tropical pycnocline to dictate the jet structure. This model jet is consistent with a number of features of the Tsuchiya jets: their roughly constant volume transports, their advection of properties such as salinity and oxygen over long zonal distances, their rapidity and narrowness, their poleward shift from west to east, the large potential vorticity gradients across them, and the pycnostad between them that builds in size and strength from west to east. However, an observed decrease in density carried by the Tsuchiya jets from west to east, not included in the model jet, suggests that diffusive or advective interaction with the surrounding ocean also may be important in subsurface countercurrent dynamics.
The subsurface countercurrents (SSCCs) in the Pacific Ocean (Tsuchiya 1972 , 1975), or Tsuchiya jets, are persistent eastward subsurface currents found on either side of the equator with a pycnostad between them. The SSCCs are remarkably steady and extend across the entire Pacific Ocean. A recent study of mean hydrographic sections from CTD data averaged on potential density anomaly surfaces in the western Pacific quantifies the SSCC locations, velocities, and transports between 137° and 165°E (Gouriou and Toole 1993). For the north SSCC they suggest that a velocity core, distinct from the Equatorial Undercurrent (EUC) and the North Equatorial Countercurrent (NECC), develops between 137° and 142°E. At 165°E Gouriou and Toole estimate a north SSCC volume transport of 11 × 106 m3 s-1 with a peak velocity of 0.27 m s-1 occurring at 2.5°N near 280-m depth. For the south SSCC, they surmise an origin between 142° and 165°E. At 165°E they estimate a transport of 7 × 106 m3 s-1, with a peak velocity of 0.22 m s-1 at 2.5°S near 280-m depth. They also note strong gradients in potential vorticity across the axes of both SSCCs and a strong gradient in salinity across the north SSCC, suggesting that the SSCCs are a barrier to meridional flow, but that between them water properties may be homogenized in gyres composed of the eastward flowing SSCCs and the westward flowing Equatorial Intermediate Current (EIC).
In the central Pacific, the Tsuchiya jets are distinctly visible in an annual mean hydrographic section nominally along 155°W from CTD data averaged on pressure surfaces (Wyrtki and Kilonsky 1984). As in the western Pacific, the north SSCC is stronger with a transport of 9 × 106 m3 s-1 and a mean velocity of 0.07 m s-1, as compared to the south SSCC, with a 4 × 106 m3 s-1 transport and a mean velocity of 0.05 m s-1. Peak velocity values are not reported but a zonal velocity section shows peak speeds <0.15 m s-1 in the north SSCC and <0.10 m s-1 in the south SSCC near 240-m depth at ±4° from the equator. These peaks are 40 m shallower and 1.5° poleward of the maxima at 165°E. These peaks are also much weaker than those at 165°E and 110°W (see below), but without commensurate changes in transports. This seeming discrepancy arises because the cross-sectional areas of the SSCCs are larger at 155°W than at 165°E and 110°W. These differences are at least partially artifacts of a shift in longitude of the mean station positions near the south SSCC which increases station spacing there. A salinity section suggests the gradient observed across the north SSCC in the western Pacific also exists in the central Pacific at 4°N. In addition, dissolved oxygen and nutrient concentration sections show that both SSCCs are associated with oxygen-rich, nutrient-poor water near ±4° latitude (Wyrtki and Kilonsky 1984), properties advected from the west (Tsuchiya 1975).
The Tsuchiya jets in the eastern Pacific are very well studied. East of 119°W, they have been described extensively by Tsuchiya (1972, 1975) through analysis of many synoptic hydrographic sections. He notes that the SSCCs exist between 3° and 6°N and 4° and 8°S, and shift poleward to the east. The north SSCC mean transport is estimated at 8 × 106 m3 s-1 with an average peak velocity of 0.27 m s-1 at depths from 30 to 200 m; the south SSCC transport is estimated at 5 × 106 m3 s-1 with an average peak velocity of 0.15 m s-1 at depths from 80 to 250 m (Tsuchiya 1975). A similar, but more recent study of the north SSCC also using analysis of several synoptic CTD sections along 110°W suggests a mean transport of 14 × 106 m3 s-1 with a mean peak velocity of 0.40 m s-1 at 4.6°N near 120 m depth (Hayes et al. 1983). The discrepancy between these two transport estimates for the north SSCC near 110°W may arise from differences in the definition of its upper boundary. The higher peak velocity estimate in the second study probably results from finer horizontal resolution of the synoptic sections. In any case, the SSCCs in the eastern Pacific are again shallower and poleward of their locations in the central Pacific with transports and velocities roughly consistent with those reported to the west. The poleward shift as the SSCCs flow eastward from 155° to 110°W has also been noted in a diagnostic calculation of the upper ocean circulation (Bryden and Brady 1985).
Finally, the water in the equatorial pycnostad in the eastern Pacific has been traced westward along the south Tsuchiya jet and then along a counterclockwise route in the subtropical gyre to a surface origin near Tasmania by Tsuchiya (1981). This work demonstrates that the properties of water on a germane isanosteric surface are modified relatively little by mixing as it is advected over great distances around the South Pacific Ocean. It is argued that vertical mixing is dominant in influencing the water properties near their surface origin, but that lateral mixing plays the stronger role farther along the subsurface flow path.
We are aware of only one theory for the dynamics of the Tsuchiya jets (McPhaden 1984). A linear, vertically diffusive model simulates the SSCCs as lobes of the EUC, formed at the poleward edge of a broad diffusive equatorial boundary layer. Within the boundary layer, downward vertical diffusion of cyclonic relative vorticity is balanced by poleward advection of planetary vorticity. Outside the boundary layer, the planetary vorticity advection is balanced by vortex stretching, creating a pycnostad. In this model, the SSCCs are the result of geostrophic balance across the pycnostad. However, in the central and eastern Pacific Ocean, the SSCCs are separated from the EUC, suggesting nonlinear dynamics may be important there (McPhaden 1984). More recently, the EUC has been modeled as an inertial jet (Pedlosky 1987, 1988, 1991), but until now no inertial model has been proposed for the SSCCs.
In this paper we use historical CTD data to create mean hydrographic profiles averaged on neutral density anomaly surfaces (Jackett and McDougall 1997) for select areal bins in the tropical Pacific Ocean, reducing the data across the entire ocean in a uniform manner designed to preserve the small meridional and vertical scales of hydrographic features found in the Tropics. We present mean meridional sections of properties at 165°E, 155°W, and 110°W together with maps of properties on and between appropriate isopycnals. These data are used in a trans-Pacific analysis to emphasize several points about the Tsuchiya jets. First, the SSCCs are separate from the EUC, at least in the central and eastern Pacific. Second, the SSCCs start near the equator in the west and shift poleward toward the east. Third, this poleward shift is correlated with a shoaling of the pycnocline and the building pycnostad between the SSCCs. We also present a simple inertial model of the SSCCs. This inertial model accounts for the roughly constant volume transports of the SSCCs, their advection of properties over long zonal distances, their persistent narrowness and rapidity, their poleward shift from west to east, the pycnostad between them that builds in size and strength from west to east, and the associated potential vorticity gradients across them.
For this study, CTD stations within different areal bins in the tropical Pacific
are averaged to make a mean hydrographic profile for each bin (Fig.
3: the dots indicate the locations of mean hydrographic profiles near the
bin centers). In latitude, the bins are centered on every 1° from 20°S to 20°N.
Bin widths are 1° in latitude, and hence include CTD stations halfway between
integer latitudes. In longitude, the bins are centered on the TAO array mooring
longitudes (McPhaden
1993), with 85°W and 126°E added as central longitudes for the far
eastern and western Pacific. Bin widths ranging from 9° to 15° of longitude
result from bin edges located midway between these nominal longitudes. This
strategy yields 13 mean meridional hydrographic sections, some better sampled
than others, which are used to make maps of properties on and between neutral
density anomaly, The CTD station data within each bin, consisting of salinity,
S, and temperature, T, as a function of pressure, P,
are averaged as a function of 
n,
surfaces, and meridional property sections at 165°E, 155°W, and 110°W, the three
best-sampled longitudes. CTD stations include all high-resolution data available
from the NODC archives, as well as those in the PMEL database from PMEL and
some other cruises not yet available from NODC. Nearly 14,000 individual CTD
stations are used, located between 20.5°S and 20.5°N latitude and between 120°E
and 80°W longitude, taken from 1967 through 1996.
The CTD station data within each bin, consisting of salinity S and
temperature T as a function of pressure P are averaged as
a function of n to create
mean hydrographic profiles. Averaging S, T, and P
as functions of n is more
involved than the conventional approach of averaging S, T,
and n as functions of P,
but the technique better preserves water properties in the sharp tropical pycnocline
(Gouriou
and Toole 1993). First, to reduce small-scale noise, individual CTD
station S and T profiles are filtered in P with a
10-dbar half-width Hanning filter and subsampled at 10-dbar intervals. Then
n is computed for these
subsampled data and averaged as a function of P to obtain a mean n(P)
profile at 10-dbar resolution. Following this step, the individually filtered
and sampled profiles of S, T, and P are linearly
interpolated to each n(P)
profile value to allow averaging of the individual CTD station data as a function
of n at roughly 10-dbar
resolution. Mean profiles for S(n),
T(n), and P(n)
are then calculated. Finally the mean P(n)
profile is used to put the mean profiles of S(n)
and T(n) onto
an even 10-dbar grid and construct a final mean n
profile.
Depth and properties of the surface mixed layer, including n,
vary over time. To construct a mixed layer for the mean profiles of S(n),
T(n), and n,
the following procedure is used. First, the mixed-layer P for each
CTD station is defined as the P above which n
is less than 0.1 kg m-3 denser than the mean n
of the top 10 dbar. Mean S and T from the surface to the mixed-layer
P are calculated for each CTD station. Then these S and T
values are averaged, weighted by the individual mixed-layer P's so
that deeper mixed-layer values get more weight, to find mean mixed-layer values
for S and T. These values are used with the mean mixed-layer
P to calculate a mean mixed-layer n.
In order to avoid n inversions
in the mean profiles, the pressure of the mean mixed-layer n
in the final mean n profile
is used to define a final mean mixed-layer P. To finish, the mean mixed-layer
S, T, and n
values are substituted into the mean S(n),
T(n), and n
profiles from the mean mixed-layer P to the surface.
The resulting 10-dbar mean hydrographic profiles are used exclusively in the
analysis. The only further smoothing performed for the mean meridional sections
presented is on the square of the buoyancy frequency, N2,
which is calculated from the mean hydrographic profiles and then smoothed with
a 30-dbar half-width Hanning filter before use. Isopycnal maps are made by linearly
interpolating the 10-dbar values of each mean hydrographic profile to the appropriate
n. These values are then
objectively mapped assuming a Gaussian covariance with correlation length scales
of 1.5° lat and 18° long and an error energy of 0.04. These correlation length
scales are roughly 1.5 times the data separation, with anisotropy appropriate
for the interior of the Tropics, where zonal scales greatly exceed meridional
scales.
Mean meridional potential temperature, 
, sections
show that the thermocline (roughly from 15° to 25°C, centered near the 20°C
isotherm) shoals and strengthens from west to east (Fig.
1). This feature is deep (120-200 m) and relatively weak at 165°E,
intermediate in depth (80-200 m) and strength at 155°W, and shallow (50-120 m)
and strong at 110°W. The poleward deepening of the thermocline south of the
equator, and north of the equator to 4°-5°N, is associated with the southern
and northern components of the westward-flowing South Equatorial Current (SEC),
respectively. The poleward shoaling of the thermocline north of 4°-5°N is associated
with the eastward-flowing NECC. The spreading of the thermocline around the
equator marks the eastward flowing EUC. This spreading is discernable at 165°E
and stronger at 155°W. At 110°W the EUC is shallow and south of the equator,
where isotherms dip near 1°S. This southern displacement from the equator has
been shown to be the result of meridional wind forcing (Philander
and Delecluse 1983). Most relevant to this study is a poleward shoaling
of isotherms below the thermocline centered near ±2.5° latitude at 165°E, ±3.5°
at 155°W, and ±4.5°-5.5° at 110°W. This shoaling shifts poleward and upward
to the east under the thermocline, marking the Tsuchiya jets. By 110°W, the
thermostad near 13°C between the SSCCs is very pronounced.
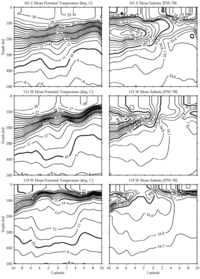
Fig. 1. Mean meridional
and S sections in the top 500 m of the ocean from 10°S to 10°N
along 165°E, 155°W, and 110°W. Contour intervals are 1°C (thick lines 5°C) for
and 0.1 PSS-78 (thick lines 0.5 PSS-78) for S. Vertical exaggeration
is 4000:1.
Mean meridional S sections show a subsurface convergence of tongues
toward the EUC (Fig. 1). The southern subsurface
S maximum, water subducted in the southern subtropics where evaporation
dominates over precipitation, is prominent in all three sections and strongest
at 155°W. North of the equator, surface S decreases to the east under
the intertropical convergence zone, a region of high precipitation (Ando
and McPhaden 1997). Salinity distributions on isopycnal surfaces
around n = 25.5
kg m-3, the core density of the EUC, suggests that the subsurface
S minimum is almost certainly a remnant of the North Pacific Intermediate
Water (Talley
1993). This fresh tongue appears to be converging along isopycnals
toward the EUC, especially at 155°W, but almost certainly takes an indirect
route involving the nearly zonal interior currents and nearly meridional western
boundary currents. At 110°W the core of the EUC is marked by an isolated S
maximum advected from the west (Hayes
et al. 1983; Lukas
1986), here found at 1°S, 65 m. Most relevant to this study,
isohalines are nearly vertical in the region of the north SSCC. The resulting
strong deep S gradient near 2°-3°N at 165°E, 2°-4°N at 155°W, and 4°-5°N
at 110°W suggests a front there and reinforces the assertion that the Tsuchiya
jets are a barrier to meridional flow (Gouriou
and Toole 1993). In addition, there is a well-defined S
minimum just north of the front, just hinted at in the sections by a pinching
of isohalines at 4°N, 5°N, and 6°N going from 165°E to 155°W to 110°W, but very
apparent in an isopycnal map discussed in the next section (Fig.
3, top panel). Since S increases from west to east, this feature
is probably fresher water being advected eastward on the northern edge of the
north SSCC.
Mean meridional n sections
(Fig. 2) are similar in appearance to those of
(Fig. 1) and
are shown primarily for reference to the isopycnal maps and the model. The previous
discussion of the thermocline and thermostad applies equally to the pycnocline
and pycnostad, with S modifying the structure slightly. However, the
mean meridional N2 sections (Fig.
2) are worthy of more discussion. The surface mixed layer is characterized
by very low N2 and shoals from 165°E to 110°W. The pycnocline,
a vertical maximum in N2, is relatively thick, deep, and
weak at 165°E. By 110°W it has thinned, nearly doubled in strength, and shoaled.
Below the pycnocline, N2 generally weakens with increasing
depth, but a very distinct equatorial pycnostad associated with the SSCCs develops,
here described as it strengthens from west to east. At 165°E, the 20 and 25 × 10-6 s-2
contours rise up at ±2° from the equator, marking a weak pycnostad centered
near n = 26.74
kg m-3 at these latitudes. By 155°W a well-developed
stability minimum is evident on both sides of the equator, with values near
12 × 10-6 s-2 at n = 26.62
kg m-3, again most extreme ±2° from the equator, but broader
in the horizontal. By 110°W the minimum is less than 10 × 10-6
s-2 near n = 26.47
kg m-3. The latitudinal distribution shows a slight increase
in stability on the equator, but the pycnostad extends from 5°S to 4°N. Thus,
as the pycnostad builds in strength and expands in area to the east, it also
shoals and its core n values
decreases by 0.27 kg m-3.
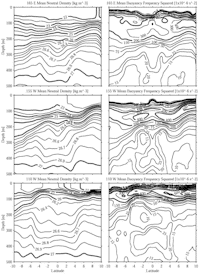
Fig. 2. As in Fig. 1 but for n
and N2. Contour intervals vary for both quantities, but
thick lines are at 1.0 kg m-3 intervals for n
and 200 × 10-6 s-2 intervals for N2.
Geostrophic volume transport and velocity calculations are made using a reference
surface of 700 dbar, near n = 27.3
kg m-3. This surface is deep enough to capture the Tsuchiya
jets and is the mean of those used in three previous quantitative works in the
region: 600 dbar at 165°E (Gouriou
and Toole 1993), 1000 dbar at 155°W (Wyrtki
and Kilonsky 1984), and 500 dbar at 110°W (Tsuchiya
1975). Table 1 lists the volume transport estimates of eastward flow
between n = 25.5
and 27.3 kg m-3. The lower limit is near the reference surface
and the upper limit is imposed to isolate the north SSCC from the eastward-flowing
NECC. Only eastward flow between the bounding latitudes contributes to the transports
in Table 1; these horizontal limits are based on a subjective examination of
the mean meridional n and
N2 sections so as to capture the eastward flow just poleward
of the equatorial pycnostad. These horizontal limits are also well defined in
that there is westward flow to either side. The SSCCs volume transports are
relatively constant, except at 165°E where the north SSCC value may be high
because some NECC flow is included in the estimate. The transport-weighted n
of the SSCCs (Table 1) are near the pycnostad core values discussed above, since
the SSCCs reside in the pycnostad, but show only a 0.09 kg m-3
decrease in n to the east,
a third of the decrease in those core values. The peak velocities shift poleward
and shoal in both hemispheres (Table 1). Peak velocities remain strong across
the Pacific except at 155°W, where the south SSCC peak velocity is weak, mostly
owing to a shift in longitude of the mean station positions (Fig. 3,
solid dots). At any rate, peak velocities from the mean sections are most likely
lower than those in synoptic sections because of the relatively large latitudinal
bin widths and temporal variability of the SSCCs core latitudes. The volume
transport estimates and peak velocity statistics are in rough accord with the
studies discussed in the introduction. However, the estimates presented here
are improved by uniform analysis of an expanded data set.
Table 1. Geostrophic volume transport
and velocity calculations made for the Pacific SSCCs using the mean meridional
sections at each longitude, referenced to 700-dbar pressure. Only eastward flow
between n = 25.5
and 27.3 kg m-3 within the latitude bounds given is used in
the transport calculations. Volume transport and transport-weighted n
remain roughly constant from west to east. Peak velocity latitudes, depths,
and magnitudes show the Tsuchiya jet cores shifting poleward, shoaling, and
maintaining speed from west to east.
| Transport calculations | Peak velocities | |||||
| Section (long) |
Latitude bounds |
Volume Transport (106 m3 s-1) |
Transport
weighted n(kg m-3) |
Peak latitude |
Peak depth (m) |
Peak magnitude (m s-1) |
| South SSCC | ||||||
| 165°E | 5°-2°S | 6.6 | 26.62 | 2.5°S | 250 | 0.17 |
| 155°W | 8°-3°S | 4.1 | 26.67 | 3.5°S | 250 | 0.07 |
| 110°W | 6°-3°S | 6.2 | 26.57 | 5.5°S | 160 | 0.16 |
| North SSCC | ||||||
| 165°E | 2°-5°N | 10.3 | 26.58 | 2.5°N | 240 | 0.26 |
| 155°W | 2°-5°N | 7.0 | 26.63 | 3.5°N | 220 | 0.21 |
| 110°W | 3°-6°N | 7.4 | 26.45 | 4.5°N | 130 | 0.21 |
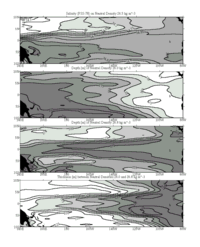
Fig. 3. Salinity on n = 26.5
kg m-3, with contour intervals of 0.05 PSS-78 and saltier
values increasingly shaded (top panel). Depth of n = 26.0
kg m-3, with contour intervals of 25 m and deeper values
increasingly shaded (second panel from top). Depth of n = 26.8
kg m-3, with contour intervals of 25 m and deeper values
increasingly shaded (third panel from top). Thickness between n = 26.0
and 26.8 kg m-3, with contour intervals of 25 m and thicker
values increasingly shaded (bottom panel). All panels are objectively mapped
from the values at each mean hydrographic profile location as described in the
text. The mapping uses the Peters projection.
Salinity on n = 26.5
kg m-3, an isopycnal near the pycnostad and within the Tsuchiya
jet cores, as defined by the transport-weighted n
just discussed, reveals a great deal about the SSCCs sources and structure
(Fig. 3). The strong S front starting
just north of the equator in the western Pacific shifts poleward and weakens
to the east. This S front suggests that the SSCCs are a barrier to
meridional flow (Gouriou
and Toole 1993), at least in the western Pacific where the front
is sharp. The meridional S minimum just north of the front is the result
of advection in the north SSCC. The only strong S contrast is near
the northern edge of the north SSCC, suggesting that the source waters for both
SSCCs are primarily from the southwestern Pacific (Tsuchiya
1981), similar to but slightly denser than the waters feeding the
EUC (Tsuchiya
et al. 1989). Salinity may also be an advective tracer for the south
SSCC, showing a faint maximum, but dissolved oxygen concentration (not analyzed
here) easily reveals both SSCCs through advectively formed isolated maxima on
isopycnals (Tsuchiya
1975; Wyrtki
and Kilonsky 1984).
The isopycnal n = 26.0
kg m-3 (Fig. 3) is near the base
of the pycnocline, above the pycnostad associated with the SSCCs (Fig.
2). The poleward deepening south of the equator, the deep values near the
equator, and those from 4° to 6°N are expressions of the southern component
of the SEC, the EUC, and the axis between the northern component of the SEC
and the NECC, respectively. However, most germane to the dynamics of the SSCCs,
the surface rises steadily to the east as does the pycnocline just above it.
In contrast, n = 26.8
kg m-3 (Fig. 3) is below the
pycnostad associated with the Tsuchiya jets, except in the far western Pacific
(Fig. 2). However, while this surface is below
the pycnostad, it is not so deep that it escapes the influence of the SSCCs.
In fact, it is at the zone of maximum vertical shear of the SSCCs in the central
Pacific, slightly above it in the western Pacific, and slightly below it in
the eastern Pacific. The strong shoaling poleward of ±2° latitude in the western
Pacific, shifting to poleward of ±4° latitude in the eastern Pacific, is the
expression of the eastward-flowing SSCCs in each hemisphere. The weaker gradient
in the Southern Hemisphere is consistent with the lower velocity and transport
estimates for the SSCC there. The slight shoaling at the equator is a shallow
signature of the EIC.
The most evocative map in terms of the Tsuchiya jet dynamics is that of thickness
between the surfaces just discussed, n = 26.0
and 26.8 kg m-3 (Fig. 3), which
bound the pycnostad core values. In the model presented below, n = 26.0
kg m-3 can be thought of as representing the pycnocline between
the surface layer and the active layer, and n = 26.8
kg m-3 the interface between the active layer and the quiescent
abyssal layer. Hence the thickness between these surfaces is that of the active
layer. This thickness map dramatically illustrates the poleward shift of the
SSCCs from west to east. It also shows the pycnostad between the SSCCs as it
builds and spreads poleward from west to east. Finally, the poleward thinning
of this layer across the axes of the SSCCs is indicative of the strong potential
vorticity gradients across them. The slight decrease in thickness on the equator
is the result of a constructive combination of the deep expression of the eastward-flowing
EUC at the upper isopycnal and the shallow expression of the westward-flowing
EIC at the lower isopycnal.
The simple model inertial jet presented below reproduces many of the properties of the Tsuchiya jets. At this point, the Tsuchiya jets have been shown to be features of the equatorial circulation that extend across much of the Pacific Ocean. Observational characteristics of the SSCCs that are reproduced by the model are their constant volume transports, their advection of properties over long zonal distances, their rapidity and narrowness, their poleward shift from west to east, the large potential vorticity gradients across them, and the pycnostad between them which builds from west to east.
The essential properties of the model are illustrated in a schematic (Fig.
4). Since the basic dynamics are the same on either side of the equator,
only the north SSCC will be modeled here in the interest of clarity and brevity.
Near the equator, the pycnocline in the Pacific shoals to the east as a result
of the near-balance in the layer above, between zonal pressure gradient and
wind stress (McPhaden
and Taft 1988). Off the equator, the pycnocline shoals to the east
as result of the near-balance of the wind stress curl and the product of poleward
mass transport and 
(Sverdrup
1947). However, the dynamics of the surface layer, here termed layer
0, have been studied extensively elsewhere. Only the observed eastward shoaling
of the pycnocline is vital to the evolution of the model jet, found in layer
1, so the pycnocline depth D, which is the interface between layer
0 and layer 1, is simply set to shoal eastward. The abyss, here termed layer
2, is assumed to be quiescent, allowing reduced-gravity dynamics to hold in
layer 1. Since layer 1 has a positive thickness, h, the depth of the
interface between layers 1 and 2 is 
= D - h.
Here D and are negative relative
to the ocean surface. With the focus on layer 1, between the prescribed pycnocline
and the quiescent abyss, the dynamics reduce to a nonlinear model with 1-1/2
layers. The model works with any specified D(x) that is a function
of the zonal direction, x, with no meridional, y, dependence.
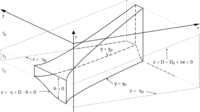
Fig. 4. Perspective view of the model
jet from 30°W of south at 30° elevation (solid lines for visible jet boundaries,
dashed lines for hidden boundaries). The surface layer is not discussed. The
pycnocline depth, D, is the interface between layer 0 and layer 1.
This interface is constant in latitude but slopes linearly up to the east (upper
plane of dotted lines). Since layer 0 is ignored, D can be thought
of as inverted topography at the top of layer 1. The interface depth between
the active layer 1 and the quiescent abyssal layer 2 is .
This deeper interface is constant on either side of the jet (lower sets of dotted
lines), but slopes up within it, where the velocity, u, is finite.
The interface depths D and
are both negative values referenced to the surface, but their difference, the
layer 1 thickness, h, is a positive quantity. The reduced gravity,
g', at
is related to the neutral density anomalies, n,
as discussed in section 5. As the pycnocline shoals to the east, the jet edges
ye and yp shift poleward as the jet
thickens, conserving Bernoulli function and potential vorticity on streamlines.
Vertical-meridional exaggeration is 167,000:1 and meridional-zonal exaggeration
is 124:1.
The inviscid momentum equations for the active layer 1 are
 |
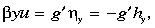(1) |
 |
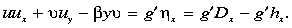(2) |
These equations are formulated assuming u » 
,
so that the meridional momentum balance is purely geostrophic but the zonal
momentum balance retains the inertial terms. The reduced gravity g' =
2g(
2 - 1)/(2 + 1)
is determined by the density difference between the quiescent abyssal layer
2 and the active layer 1 (Fig. 4), where
= n + 1000 kg m-3.
The continuity equation is
 |
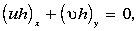(3) |
so a transport streamfunction, 
(x,y),
can be defined as
 |
(4a, 4b) |
satisfying (3). From (1) and (2) the Bernoulli function,
 |
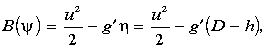(5) |
which includes the zonal kinetic energy as a result of retaining
inertial terms in (2), is conserved following fluid parcels, and therefore must
be a function of
alone. Furthermore, the potential vorticity,
 |
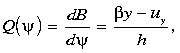(6) |
being the derivative of the Bernoulli function with respect to streamfunction, is also conserved on streamlines. The potential vorticity includes relative vorticity from meridional variations in zonal velocity as a result of retaining inertial terms in (2),
The model boundary conditions are set as follows. At the western edge of the
model domain, longitude x = x0 (140°E),
an inflow profile uo(y) is specified in the active layer,
bounded by quiescent fluid at both the equatorward, ye,
and poleward, yp, edges. Specifying an equatorward interface
depth, e,
at y = ye and integrating (1) with respect to
y gives the corresponding layer interface depth, 0(y).
After integrating (4a) to find
at x = x0, (5) and (6) are used to find
B() and
Q(). It
follows from (1) that, since the fluid is quiescent outside the model jet, the
interface depths at its edges, e
and p,
are both constants. The jet edges are streamlines, e
and p,
so applying (5) shows that zonal speeds at the edges, ue
and up, are also constants.
Equations (4a), (5), and (6) can be recast as a set of coupled first-order differential equations:
 |
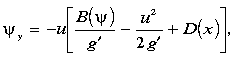(7) |
 |
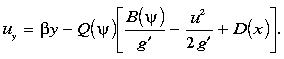(8) |
At each longitude, we guess the location of ye, integrate
(7) and (8) until
= p,
check to see if u = up there, and if not, repeat
the process, adjusting ye until this condition is met. This
solution algorithm has been used before for similar problems (Pedlosky
1987). A monotonic potential vorticity profile across the model jet
maintains sufficient conditions for stability of the basic state (Pedlosky
1979).
A number of integrations were carried out, but only one is presented here.
The model pycnocline depth is chosen as D(x) = Do + sx,
and shoals linearly with s = 1.1305 × 10-5
from - 237.5 m at 140°E, the western edge of the model domain,
to -62.5 m at 80°W, the eastern edge of the domain. Here u0(y)
at x0 = 140°E is chosen as a Gaussian with ue = 0.05 m s-1,
up = 0.05 m s-1, a peak velocity
of 0.25 m s-1 at 2.26°N, a decay scale of 0.72° lat, and
edges at 0.09° and 4.61°N. The reduced gravity g' = 5 × 10-3
m s-2, a value characteristic of the density difference between
the abyss and the pycnostad. Setting e = -375 m
and integrating to yp gives 0(y)
and p = -300 m.
The net transport is 7.0 × 106 m3 s-1,
close to values of the observed SSCC (Table 1).
For these initial conditions, when (7) and (8) are integrated at x0,
three solutions are found. The existence of multiple solutions should not be
too much of a surprise since the dynamical system is nonlinear and the model
jet edges are free to vary their position. The first solution is the original
Gaussian. A second solution is slightly narrower, with edges shifted poleward
to 0.48° and 4.86°N, a peak velocity of 0.27 m s-1 at 2.20°N,
and an interior velocity minimum near the north edge. The third solution is
the narrowest, a blunted triangular velocity profile extending from 0.68° to
3.77°N with a maximum value of 0.30 m s-1 at 2.25°N (Figs.
4 and 5). The first two solutions get broader,
slower, and quickly develop interior zonal flow minima and then reversals as
the pycnocline shoals to the east. Flow reversals make it impossible to calculate
a solution with the simple procedure outlined here, so we cannot follow these
solutions across the entire domain. The third solution narrows, accelerates,
and does not develop interior flow minima or reversals as the pycnocline shoals
to the east. This third, jetlike solution can be found across the entire domain
and is chosen as the preferable one. E. Firing (1995, personal communication)
has also pointed out that the narrowest, fastest jet has the lowest total energy
for a given B()
and transport, making it plausibly the most stable flow. This solution does
not match u0(y) and 0(y),
so it is substituted as the initial condition at longitude x0
and carried eastward.
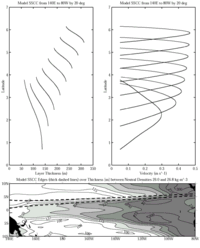
Fig. 5. Active layer thickness within the
model jet plotted against latitude from 140°E to 80°W at 20° intervals (top
left panel) and velocity plotted against latitude from 140°E to 80°W at 20°
intervals (top right panel). Jet edges (thick dashed lines in bottom panel)
are plotted over thickness between n = 26.0
and 26.8 kg m-3 as in the bottom panel of Fig.
3. The jet shifts poleward, narrows in the meridional, thickens in the vertical,
and accelerates to the east as a consequence of conservation of potential vorticity
and Bernoulli function under the shoaling pycnocline.
The solution dynamics are simple. The model is inviscid, so the boundary values
at the western edge of the model jet and the zonal slope of the pycnocline determine
its evolution across the basin. As the jet moves eastward, it is stretched vertically
by the shoaling pycnocline over the quiescent abyss, hence it shifts poleward
to conserve Q. As the jet becomes thicker in the vertical to the east
it accelerates and narrows in the horizontal to conserve transport. Retention
of the inertial terms in (2) allows the jet to narrow and accelerate, making
relative vorticity important in Q conservation near the jet edges.
A totally different behavior is predicted if the model is formulated using the
dynamics of the ventilated thermocline theory (Luyten
et al. 1983), where the geostrophic balance holds for both momentum
equations but the continuity equation remains nonlinear. In this case, the interface
depth alone gives the Bernoulli function and the potential vorticity contains
only the planetary term. Streamlines follow y/h
contours, so they originate on the equator and shift poleward to the east in
direct proportion to the increase in active layer thickness caused by the shoaling
pycnocline. The streamlines under the ventilated thermocline dynamics diverge
to the east whereas those of the chosen inertial solution converge. Hence, the
inclusion of inertial terms, retaining relative vorticity and kinetic energy
in the dynamics, is central to the character of the model jet presented here.
We derive a simple measure of the poleward shift as the model jet moves eastward. The streamfunction-weighted latitude of the jet, <y>, written in streamfunction coordinates, is
 |
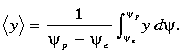(9) |
Some manipulation leads to an expression for <y> as proportional to the means and differences of various quantities at the jet edges
 |
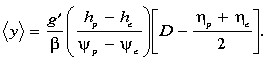(10) |
The term inside the square brackets can also be written as (hp + he)/2. Thus <y> shifts poleward more quickly if the reduced gravity is large, the difference in interface depths at the jet edges is large, the net transport is small, or the pycnocline slope to the east is large.
The model jet shifts poleward just as predicted by the <y> expression (Figs. 4 and 5). The model parameters give a <y> that starts at 2.1°N at 140°E and reaches 5.8°N by 80°W. Mean layer thicknesses within the jet increase steadily from 106 to 278 m from west to east, a factor of 2.62. The jet narrows from 3.09° to 0.72° latitude, by a factor of 0.233. The jet accelerates from a mean velocity of 0.19 to 0.31 m s-1 from west to east, a factor of 1.63. Multiplication of these factors to obtain unity illustrates how transport is conserved within the jet. As the jet narrows and thickens, the thickness increase is offset by a poleward shift in latitude to conserve potential vorticity overall (Figs. 4 and 5). The relative vorticity becomes very large at the edges of the jet to conserve potential vorticity there. At the equatorward edge the tendency of the relative vorticity is to reduce the magnitude of the potential vorticity while at the poleward edge the tendency is to increase it. This growth of relative vorticity near the edges is accomplished through the narrowing of the jet and an increase in the peak velocity from 0.30 to 0.47 m s-1 from west to east (Figs. 4 and 5).
The model does not consider the origin of the Tsuchiya jets. One possibility is that in the western Pacific the Tsuchiya jets are generated as lobes of the EUC under the diffusive dynamics discussed by McPhaden (1984). These lobes could separate from the EUC in the east due to the poleward shift forced by the shoaling thermocline, as discussed here, and propagate nearly inertially. However, vertical friction sufficiently strong to spin up the SSCCs in the western Pacific would likely damp them out in the central Pacific. Another possibility for their origin is a current at the western boundary turning east, similar to the way in which the EUC appears to be fed in observations and models (Tsuchiya et al. 1989; Pedlosky 1991). While observations suggest the south SSCC is fed by water from the south (Tsuchiya 1981), the north SSCC appears to have contributions from both hemispheres (Bingham and Lukas 1995).
In the eastern Pacific another interesting problem arises: the termination of the Tsuchiya jets. In an inertial model of the EUC, the right strength of diffusive upwelling at the equator can remove mass from the EUC as it flows eastward, terminating it at the eastern boundary (Pedlosky 1988). It seems likely that vertical diffusive processes, at or away from the equator, could be included in a more complex model of the SSCCs to model their termination. It is possible that vertical diffusive processes could take place within the SSCCs. Alternatively, the pycnostad between the SSCCs does intersect the equator, and might allow strong vertical processes there to be connected to the SSCCs. We know of no observational study describing the fate of the north SSCC. However, observations suggest that the EUC and the south SSCC turn south at the eastern boundary to feed the Peru-Chile undercurrent and countercurrent (Lukas 1986). This observational work seems to preclude the total dominance of vertical processes in determining the fate of the EUC and the SSCCs.
One interesting feature of the observations not explained by the model is the
decrease of transport-weighted n
in the Tsuchiya jets from west to east. This decrease, if it is significant
in the face of the many uncertainties present in the transport calculations,
suggests that mixing processes in the ocean may play some role in the SSCCs
dynamics. These mixing processes presumably do work to diffuse the SSCCs, altering
the potential vorticity distribution within them by decreasing the magnitude
of the relative vorticity on their edges. The model results suggests that the
tendency toward potential vorticity conservation in the ocean overcomes the
effects of mixing to keep the Tsuchiya jets focused and shifting poleward by
vortex stretching under the shoaling pycnocline.
Acknowledgments. This work was funded by the Climate and Global Change Program through the NOAA Office of Global Programs and by the NOAA Pacific Marine Environmental Laboratory. LuAnne Thompson provided insightful advice on model formulation and integration. Julian McCreary and Eric Firing made numerous helpful suggestions to improve the manuscript. Nancy Soreide, Marie Schall, Dai McClurg, and Stephan Zube all helped with programming and database management. Kristene McTaggart calibrated a great deal of the PMEL CTD data used in this work.
Ando, K., and M. J. McPhaden, 1997: Variability of surface layer hydrography in the tropical Pacific Ocean. J. Geophys. Res., 102, 23,063-23,078.
Bingham, F. M., and R. Lukas, 1995: The distribution of intermediate water in the western equatorial Pacific during January-February 1986. Deep-Sea Res. II, 42, 1545-1573.
Bryden, H. L., and E. C. Brady, 1985: Diagnostic model of the three-dimensional circulation in the upper equatorial Pacific Ocean. J. Phys. Oceanogr., 15, 1255-1273.
Gouriou, Y., and J. Toole, 1993: Mean circulation of the upper layers of the western equatorial Pacific Ocean. J. Geophys. Res., 98, 22,495-22,520.
Hayes, S. P., J. M. Toole, and L. J. Mangum, 1983: Water-mass and transport variability at 110°W in the equatorial Pacific. J. Phys. Oceanogr., 13, 153-168.
Jackett, D., and T. J. McDougall, 1997: A neutral density variable for the world's ocean. J. Phys. Oceanogr., 27, 237-263.
Lukas, R., 1986: The termination of the equatorial undercurrent in the eastern Pacific. Prog. Oceanogr., 16, 63-90.
Luyten, J. R., J. Pedlosky, and H. Stommel, 1983: The ventilated thermocline. J. Phys. Oceanogr., 13, 292-309.
McPhaden, M. J., 1984: On the dynamics of equatorial subsurface countercurrents. J. Phys. Oceanogr., 14, 1216-1225.
McPhaden, M. J., 1993: TOGA-TAO and the 1991-1993 El Niño-Southern Oscillation event. Oceanography, 6, 36-44.
McPhaden, M. J., and B. A. Taft., 1988: Dynamics of seasonal and intraseasonal variability in the eastern equatorial Pacific. J. Phys. Oceanogr., 18, 1713-1732.
Pedlosky, J., 1979: Geophysical Fluid Dynamics. Springer-Verlag, 624 pp.
Pedlosky, J., 1987: An inertial theory of the Equatorial Undercurrent. J. Phys. Oceanogr., 17, 1978-1985.
Pedlosky, J., 1988: Entrainment and the termination of the Equatorial Undercurrent. J. Phys. Oceanogr., 18, 880-886.
Pedlosky, J., 1991: The link between western boundary currents and equatorial undercurrents. J. Phys. Oceanogr., 21, 1553-1558.
Philander, S. G. H., and P. Delecluse, 1983: Coastal currents in low latitudes (with application to the Somali and El Niño currents). Deep-Sea Res., 30, 887-902.
Sverdrup, H. U., 1947: Wind-driven currents in a baroclinic ocean with application to the equatorial currents of the eastern Pacific. Proc. Natl. Acad. Sci., 33, 318-326.
Talley, L. D., 1993: Distribution and formation of North Pacific Intermediate Water, J. Phys. Oceanogr., 23, 517-537.
Tsuchiya, M., 1972: A subsurface north equatorial countercurrent in the eastern Pacific Ocean. J. Geophys. Res., 77, 5981-5986.
Tsuchiya, M., 1975: Subsurface countercurrents in the eastern equatorial Pacific Ocean. J. Mar. Res., 33(Suppl.), 145-175.
Tsuchiya, M., 1981: The origin of the Pacific equatorial 13°C water. J. Phys. Oceanogr., 11, 794-812.
Tsuchiya, M., R. Lukas, R. A. Fine, E. Firing, and E. Lindstrom, 1989: Source waters of the Pacific Equatorial Undercurrent. Progress in Oceanography, Vol. 23, Pergamon Press, 101-147.
Wyrtki, K., and B. Kilonsky, 1984: Mean water and current structure during the Hawaii-to-Tahiti shuttle experiment. J. Phys. Oceanogr., 14, 242-254.
Return to Abstract