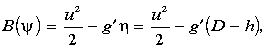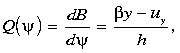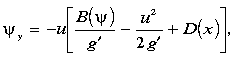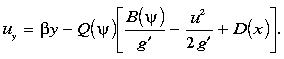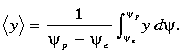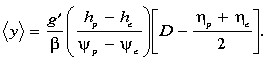The Pacific Subsurface Countercurrents and an Inertial Model

Gregory C. Johnson and Dennis W. Moore

National Oceanic and Atmospheric Administration/Pacific Marine Environmental Laboratory, Seattle, Washington

Journal of Physical Oceanography, 27, 2448-2459
Not subject to U.S. copyright. Published in 1997 by the American Meterological Society.

5. An inertial model

The simple model inertial jet presented below reproduces many of the properties of the Tsuchiya jets. At this point, the Tsuchiya jets have been shown to be features of the equatorial circulation that extend across much of the Pacific Ocean. Observational characteristics of the SSCCs that are reproduced by the model are their constant volume transports, their advection of properties over long zonal distances, their rapidity and narrowness, their poleward shift from west to east, the large potential vorticity gradients across them, and the pycnostad between them which builds from west to east.

The essential properties of the model are illustrated in a schematic (Fig. 4). Since the basic dynamics are the same on either side of the equator, only the north SSCC will be modeled here in the interest of clarity and brevity. Near the equator, the pycnocline in the Pacific shoals to the east as a result of the near-balance in the layer above, between zonal pressure gradient and wind stress (McPhaden and Taft 1988). Off the equator, the pycnocline shoals to the east as result of the near-balance of the wind stress curl and the product of poleward mass transport and (Sverdrup 1947). However, the dynamics of the surface layer, here termed layer 0, have been studied extensively elsewhere. Only the observed eastward shoaling of the pycnocline is vital to the evolution of the model jet, found in layer 1, so the pycnocline depth D, which is the interface between layer 0 and layer 1, is simply set to shoal eastward. The abyss, here termed layer 2, is assumed to be quiescent, allowing reduced-gravity dynamics to hold in layer 1. Since layer 1 has a positive thickness, h, the depth of the interface between layers 1 and 2 is  = D - h. Here D and  are negative relative to the ocean surface. With the focus on layer 1, between the prescribed pycnocline and the quiescent abyss, the dynamics reduce to a nonlinear model with 1-1/2 layers. The model works with any specified D(x) that is a function of the zonal direction, x, with no meridional, y, dependence.

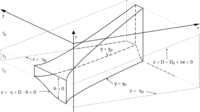
Fig. 4. Perspective view of the model jet from 30°W of south at 30° elevation (solid lines for visible jet boundaries, dashed lines for hidden boundaries). The surface layer is not discussed. The pycnocline depth, D, is the interface between layer 0 and layer 1. This interface is constant in latitude but slopes linearly up to the east (upper plane of dotted lines). Since layer 0 is ignored, D can be thought of as inverted topography at the top of layer 1. The interface depth between the active layer 1 and the quiescent abyssal layer 2 is . This deeper interface is constant on either side of the jet (lower sets of dotted lines), but slopes up within it, where the velocity, u, is finite. The interface depths D and are both negative values referenced to the surface, but their difference, the layer 1 thickness, h, is a positive quantity. The reduced gravity, g', at is related to the neutral density anomalies, _n, as discussed in section 5. As the pycnocline shoals to the east, the jet edges y_e and y_p shift poleward as the jet thickens, conserving Bernoulli function and potential vorticity on streamlines. Vertical-meridional exaggeration is 167,000:1 and meridional-zonal exaggeration is 124:1.

The inviscid momentum equations for the active layer 1 are

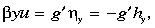(1)

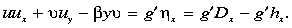(2)

These equations are formulated assuming u » , so that the meridional momentum balance is purely geostrophic but the zonal momentum balance retains the inertial terms. The reduced gravity g' = 2g(₂ - ₁)/(₂ + ₁) is determined by the density difference between the quiescent abyssal layer 2 and the active layer 1 (Fig. 4), where   = _n + 1000 kg m^-3. The continuity equation is

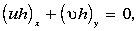(3)

so a transport streamfunction, (x,y), can be defined as

(4a, 4b)

satisfying (3). From (1) and (2) the Bernoulli function,

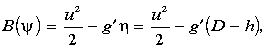(5)

which includes the zonal kinetic energy as a result of retaining inertial terms in (2), is conserved following fluid parcels, and therefore must be a function of alone. Furthermore, the potential vorticity,

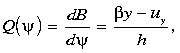(6)

being the derivative of the Bernoulli function with respect to streamfunction, is also conserved on streamlines. The potential vorticity includes relative vorticity from meridional variations in zonal velocity as a result of retaining inertial terms in (2),

The model boundary conditions are set as follows. At the western edge of the model domain, longitude x = x₀ (140°E), an inflow profile u_o(y) is specified in the active layer, bounded by quiescent fluid at both the equatorward, y_e, and poleward, y_p, edges. Specifying an equatorward interface depth, _e, at y = y_e and integrating (1) with respect to y gives the corresponding layer interface depth, ₀(y). After integrating (4a) to find at x = x₀, (5) and (6) are used to find B() and Q(). It follows from (1) that, since the fluid is quiescent outside the model jet, the interface depths at its edges, _e and _p, are both constants. The jet edges are streamlines, _e and _p, so applying (5) shows that zonal speeds at the edges, u_e and u_p, are also constants.

Equations (4a), (5), and (6) can be recast as a set of coupled first-order differential equations:

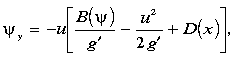(7)

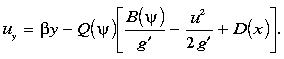(8)

At each longitude, we guess the location of y_e, integrate (7) and (8) until = _p, check to see if u = u_p there, and if not, repeat the process, adjusting y_e until this condition is met. This solution algorithm has been used before for similar problems (Pedlosky 1987). A monotonic potential vorticity profile across the model jet maintains sufficient conditions for stability of the basic state (Pedlosky 1979).

A number of integrations were carried out, but only one is presented here. The model pycnocline depth is chosen as D(x) = D_o + sx, and shoals linearly with s = 1.1305 × 10^-5 from - 237.5 m at 140°E, the western edge of the model domain, to -62.5 m at 80°W, the eastern edge of the domain. Here u₀(y) at x₀ = 140°E is chosen as a Gaussian with u_e = 0.05 m s^-1, u_p = 0.05 m s^-1, a peak velocity of 0.25 m s^-1 at 2.26°N, a decay scale of 0.72° lat, and edges at 0.09° and 4.61°N. The reduced gravity g' = 5 × 10^-3 m s^-2, a value characteristic of the density difference between the abyss and the pycnostad. Setting _e = -375 m and integrating to y_p gives ₀(y) and _p = -300 m. The net transport is 7.0 × 10⁶ m³ s^-1, close to values of the observed SSCC (Table 1).

For these initial conditions, when (7) and (8) are integrated at x₀, three solutions are found. The existence of multiple solutions should not be too much of a surprise since the dynamical system is nonlinear and the model jet edges are free to vary their position. The first solution is the original Gaussian. A second solution is slightly narrower, with edges shifted poleward to 0.48° and 4.86°N, a peak velocity of 0.27 m s^-1 at 2.20°N, and an interior velocity minimum near the north edge. The third solution is the narrowest, a blunted triangular velocity profile extending from 0.68° to 3.77°N with a maximum value of 0.30 m s^-1 at 2.25°N (Figs. 4 and 5). The first two solutions get broader, slower, and quickly develop interior zonal flow minima and then reversals as the pycnocline shoals to the east. Flow reversals make it impossible to calculate a solution with the simple procedure outlined here, so we cannot follow these solutions across the entire domain. The third solution narrows, accelerates, and does not develop interior flow minima or reversals as the pycnocline shoals to the east. This third, jetlike solution can be found across the entire domain and is chosen as the preferable one. E. Firing (1995, personal communication) has also pointed out that the narrowest, fastest jet has the lowest total energy for a given B() and transport, making it plausibly the most stable flow. This solution does not match u₀(y) and ₀(y), so it is substituted as the initial condition at longitude x₀ and carried eastward.

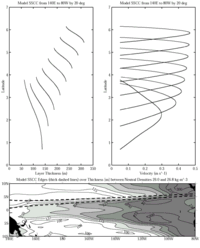
Fig. 5. Active layer thickness within the model jet plotted against latitude from 140°E to 80°W at 20° intervals (top left panel) and velocity plotted against latitude from 140°E to 80°W at 20° intervals (top right panel). Jet edges (thick dashed lines in bottom panel) are plotted over thickness between _n = 26.0 and 26.8 kg m^-3 as in the bottom panel of Fig. 3. The jet shifts poleward, narrows in the meridional, thickens in the vertical, and accelerates to the east as a consequence of conservation of potential vorticity and Bernoulli function under the shoaling pycnocline.

The solution dynamics are simple. The model is inviscid, so the boundary values at the western edge of the model jet and the zonal slope of the pycnocline determine its evolution across the basin. As the jet moves eastward, it is stretched vertically by the shoaling pycnocline over the quiescent abyss, hence it shifts poleward to conserve Q. As the jet becomes thicker in the vertical to the east it accelerates and narrows in the horizontal to conserve transport. Retention of the inertial terms in (2) allows the jet to narrow and accelerate, making relative vorticity important in Q conservation near the jet edges. A totally different behavior is predicted if the model is formulated using the dynamics of the ventilated thermocline theory (Luyten et al. 1983), where the geostrophic balance holds for both momentum equations but the continuity equation remains nonlinear. In this case, the interface depth alone gives the Bernoulli function and the potential vorticity contains only the planetary term. Streamlines follow y/h contours, so they originate on the equator and shift poleward to the east in direct proportion to the increase in active layer thickness caused by the shoaling pycnocline. The streamlines under the ventilated thermocline dynamics diverge to the east whereas those of the chosen inertial solution converge. Hence, the inclusion of inertial terms, retaining relative vorticity and kinetic energy in the dynamics, is central to the character of the model jet presented here.

We derive a simple measure of the poleward shift as the model jet moves eastward. The streamfunction-weighted latitude of the jet, <y>, written in streamfunction coordinates, is

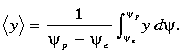(9)

Some manipulation leads to an expression for <y> as proportional to the means and differences of various quantities at the jet edges

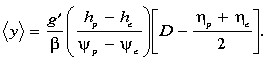(10)

The term inside the square brackets can also be written as (h_p + h_e)/2. Thus <y> shifts poleward more quickly if the reduced gravity is large, the difference in interface depths at the jet edges is large, the net transport is small, or the pycnocline slope to the east is large.

The model jet shifts poleward just as predicted by the <y> expression (Figs. 4 and 5). The model parameters give a <y> that starts at 2.1°N at 140°E and reaches 5.8°N by 80°W. Mean layer thicknesses within the jet increase steadily from 106 to 278 m from west to east, a factor of 2.62. The jet narrows from 3.09° to 0.72° latitude, by a factor of 0.233. The jet accelerates from a mean velocity of 0.19 to 0.31 m s^-1 from west to east, a factor of 1.63. Multiplication of these factors to obtain unity illustrates how transport is conserved within the jet. As the jet narrows and thickens, the thickness increase is offset by a poleward shift in latitude to conserve potential vorticity overall (Figs. 4 and 5). The relative vorticity becomes very large at the edges of the jet to conserve potential vorticity there. At the equatorward edge the tendency of the relative vorticity is to reduce the magnitude of the potential vorticity while at the poleward edge the tendency is to increase it. This growth of relative vorticity near the edges is accomplished through the narrowing of the jet and an increase in the peak velocity from 0.30 to 0.47 m s^-1 from west to east (Figs. 4 and 5).

Return to previous section or go to next section

PMEL Outstanding Papers

PMEL Publications Search

PMEL Homepage