U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
The terms in the surface heat flux into the mixed layer can be estimated using the bulk formulae. These relations are discussed in several recent references [e.g., McPhaden, 1982; Stevenson and Niiler, 1983; Reed, 1983; Dobson and Smith, 1988; Weare, 1989]. The equations used here are those of Reed [1983]; their accuracy is evaluated in Dobson and Smith [1988]. Specifically, the surface heat flux terms in (1) are given by:
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
In (2), Q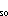 is the clear sky radiance [Reed,
1977, 1983],
C the cloudiness (tenths) and
is the clear sky radiance [Reed,
1977, 1983],
C the cloudiness (tenths) and  is the
noon solar altitude (degree). The clear sky radiance and alpha are evaluated
using a harmonic formula which introduces latitudinal and annual variations.
In (3),
is the
noon solar altitude (degree). The clear sky radiance and alpha are evaluated
using a harmonic formula which introduces latitudinal and annual variations.
In (3),  =
0.97 is the emissivity of the ocean;
=
0.97 is the emissivity of the ocean; ![]() = 5.67 × 10
= 5.67 × 10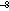 W m
W m °K
°K is the Stefan-Boltzmann constant, e
is the atmospheric vapor pressure. In (4) and
(5),
is the Stefan-Boltzmann constant, e
is the atmospheric vapor pressure. In (4) and
(5), 
 = 1.15 × 10
= 1.15 × 10 g cm
g cm is the air density, C
is the air density, C = 1.2
× 10
= 1.2
× 10 is the exchange coefficient, L
= 2440 J g
is the exchange coefficient, L
= 2440 J g is the latent heat of vaporization,
V is the wind speed at a nominal height of 10 m, q
is the latent heat of vaporization,
V is the wind speed at a nominal height of 10 m, q is the specific humidity saturated at the sea temperature, q
is the specific humidity saturated at the sea temperature, q is the specific humidity of the air at 10 m elevation, and T
is the specific humidity of the air at 10 m elevation, and T and T
and T are the air and sea
temperatures. Equation (6) estimates the heat
loss by radiation which penetrates through the mixed layer. This exponential
decay law is taken from Ivanov
[1977] with
are the air and sea
temperatures. Equation (6) estimates the heat
loss by radiation which penetrates through the mixed layer. This exponential
decay law is taken from Ivanov
[1977] with ![]() =
0.04 m
=
0.04 m . The mixed layer depth, h
. The mixed layer depth, h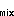 ,
is estimated as discussed below.
,
is estimated as discussed below.
The mooring measurements provided information on wind speed, SST and air temperature.
In order to apply equations (2-5), we used the mooring data supplemented by
Comprehensive Ocean-Atmosphere Data Set (COADS) marine surface climatology.
Measured winds and air temperature were used without correcting the measurement
height to 10 m. Assuming a logarithmic profile with neutral stability and a
constant drag coefficient of 1.2 × 10 [Large
and Pond, 1982], an increase of wind speed by 8% would account for the
measurement height. This correction was not made because of the uncertainties
in the assumptions used to derive it. The saturation humidity q
[Large
and Pond, 1982], an increase of wind speed by 8% would account for the
measurement height. This correction was not made because of the uncertainties
in the assumptions used to derive it. The saturation humidity q in (4) was evaluated from the Clausius-Clapeyron
equation using the observed SST. Cloud cover and relative humidity were obtained
from a monthly mean COADS climatology for 1946-85 [Deser,
1989]. For comparison, monthly mean values based on COADS data for 1986-1988
were also used (C. Deser, personal communication, 1989). Liu
and Niiler [1990] discuss the sensitivity of the latent heat flux to
variations in humidity.
in (4) was evaluated from the Clausius-Clapeyron
equation using the observed SST. Cloud cover and relative humidity were obtained
from a monthly mean COADS climatology for 1946-85 [Deser,
1989]. For comparison, monthly mean values based on COADS data for 1986-1988
were also used (C. Deser, personal communication, 1989). Liu
and Niiler [1990] discuss the sensitivity of the latent heat flux to
variations in humidity.
After smoothing with a 91-day Hanning filter, the estimated surface flux terms
are shown in Figure 4. The incoming shortwave
radiation is based solely on climatology. It has a semiannual variation associated
with the sun passing over the equator twice each year. No interannual variability
is possible because climatological monthly cloud cover is used in (2).
The mean value is about 250 W m and the
standard deviation of the low pass filtered time series is about 15 W m
and the
standard deviation of the low pass filtered time series is about 15 W m .
These results are consistent with Reed
[1983].
.
These results are consistent with Reed
[1983].
Fig. 4. Components of the surface heat flux (see equation (1)).
The estimated latent heat flux undergoes both annual and interannual variations.
Latent heat flux is minimum in March, when wind speed is low (Figure
3), and maximum in boreal autumn. The minimum in March of 1987 is almost
twice the March value in 1986 or 1988. This increase in latent heat release
is related to the warm SST anomalies and higher wind speeds that occurred in
the eastern Pacific during the 1987 El Niño. The mean latent heat flux is approximately
45 W m , which again agrees with Reed's
result, and the standard deviation is about 12 W m
, which again agrees with Reed's
result, and the standard deviation is about 12 W m .
.
The longwave radiation is almost a constant value of 35 W m over the record length and thus does not contribute significantly to the change
in the total heat flux. The sensible heat flux depends on the air-sea temperature
difference. Previous studies in the Pacific Ocean [Reed,
1977, 1983;
Weare
et al., 1981; Esbensen
and Kushnir, 1981] have shown that this heat flux is small (about 10
W m
over the record length and thus does not contribute significantly to the change
in the total heat flux. The sensible heat flux depends on the air-sea temperature
difference. Previous studies in the Pacific Ocean [Reed,
1977, 1983;
Weare
et al., 1981; Esbensen
and Kushnir, 1981] have shown that this heat flux is small (about 10
W m ). Since some of the air temperature
data are missing from the equatorial mooring record, we were unable to compute
the sensible heat flux over the entire record length. However, whenever possible
the calculation was made and the mean (and standard deviation) of Q
). Since some of the air temperature
data are missing from the equatorial mooring record, we were unable to compute
the sensible heat flux over the entire record length. However, whenever possible
the calculation was made and the mean (and standard deviation) of Q was less than 5 W m
was less than 5 W m . Thus Q
. Thus Q was ignored in subsequent calculations.
was ignored in subsequent calculations.
Because mixed layer depth is shallow in the eastern Pacific, incoming solar
radiation cannot be completely absorbed within the layer. On average, about
50 W m penetrates into the deep ocean. This
penetrative radiation is strongest during springtime when the mixed layer is
shallow (Figure 5). Thus although the solar radiation
is strongest in spring season, the net heating received by the mixed layer is
not necessarily largest at that time. Indeed, the net heating within the mixed
layer, Q
penetrates into the deep ocean. This
penetrative radiation is strongest during springtime when the mixed layer is
shallow (Figure 5). Thus although the solar radiation
is strongest in spring season, the net heating received by the mixed layer is
not necessarily largest at that time. Indeed, the net heating within the mixed
layer, Q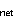 , in Figure
4, is maximum in the fall of 1986. The penetration of radiation through
the mixed layer reduces the annual variation of the net solar heating. The mean
value of the net heating within the mixed layer is 115 W m
, in Figure
4, is maximum in the fall of 1986. The penetration of radiation through
the mixed layer reduces the annual variation of the net solar heating. The mean
value of the net heating within the mixed layer is 115 W m with a standard deviation of 10 W m
with a standard deviation of 10 W m . The
mean heat flux at the surface is 165 W m
. The
mean heat flux at the surface is 165 W m ,
comparable to the 150 W m
,
comparable to the 150 W m value determined
by Reed
[1983] for the eastern equatorial Pacific.
value determined
by Reed
[1983] for the eastern equatorial Pacific.
Fig. 5. Contour plots of (a) isotherm depth (contours are in degrees
Celsius), (b) zonal velocity (centimeters per second), and (c)
meridional velocity (centimeters per second) in the upper 100 m at 0°, 110°W,
based on the 91-day low-pass-filtered time series. The dashed line superimposed
on the isotherm contours indicates the mixed layer depth computed as discussed
in the text. Contour intervals are 1°C, 20 cm s ,
and 5 cm s
,
and 5 cm s for temperature, zonal velocity,
and meridional velocity, respectively.
for temperature, zonal velocity,
and meridional velocity, respectively.
Sources of errors in Q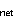 can come from both random and systematic uncertainties in the basic observations
and in the parameters in the bulk formulae. Recent studies by Weare
[1989] indicate that the uncertainties in monthly mean climatological estimates
of the surface heat flux components over the eastern tropical Pacific are 20
W m
can come from both random and systematic uncertainties in the basic observations
and in the parameters in the bulk formulae. Recent studies by Weare
[1989] indicate that the uncertainties in monthly mean climatological estimates
of the surface heat flux components over the eastern tropical Pacific are 20
W m for the solar radiation, 10 W m
for the solar radiation, 10 W m for longwave radiation, 35 W m
for longwave radiation, 35 W m for latent
heat flux, and 5 W m
for latent
heat flux, and 5 W m for sensible heat flux,
which leads to a total error of 40 W m
for sensible heat flux,
which leads to a total error of 40 W m for
the net surface heat flux. The uncertainties of the variability of heat fluxes
should be smaller than the error in absolute flux because systematic errors
in the observations and bulk formulae may cancel upon differencing. However,
our estimates have an additional uncertainty associated with the use of climatological
data combined with mooring data for specific years. Comparison of the fluxes
computed from climatological values of cloud cover and relative humidity (Figure
4) with those estimated using 1986-1988 COADS data show an rms difference
of about 10 W m
for
the net surface heat flux. The uncertainties of the variability of heat fluxes
should be smaller than the error in absolute flux because systematic errors
in the observations and bulk formulae may cancel upon differencing. However,
our estimates have an additional uncertainty associated with the use of climatological
data combined with mooring data for specific years. Comparison of the fluxes
computed from climatological values of cloud cover and relative humidity (Figure
4) with those estimated using 1986-1988 COADS data show an rms difference
of about 10 W m . Thus, the deviations from
climatology of cloud cover and humidity during the study period were relatively
small. The climatological values were used in the remaining calculations since
the statistical reliability of these estimates is higher.
. Thus, the deviations from
climatology of cloud cover and humidity during the study period were relatively
small. The climatological values were used in the remaining calculations since
the statistical reliability of these estimates is higher.
Go back to previous section or forward to next section