U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
Using COADS data for the period 1946-1993, the near-global SLP variability associated with the climatological seasonal march and interannual variability is discussed. A particular focus concerns the patterns associated with the two years before and after the South American sea surface temperatures rise (El Niño). The ten El Niño events in this record are composited, and the robustness of the features of this composite is tested.
Many features of the composite are quite robust; they occur during most El Niño events and are infrequent during non-El Niño periods. The most robust feature is an area of low SLP anomaly (SLPA) in the eastern equatorial Pacific during Year(0) of the composite. This feature exceeds significance thresholds during every El Niño year and never during non-El Niño years; it correlates better with central Pacific SST variability than does the SOI. A west-central north Pacific positive SLPA, occurring late in Year(0) and lasting into Spring of Year(+1) is the second most robust feature. Strong SLPA signals occur in the eastern south Pacific and around Australia in many events, but the behavior varies greatly from event to event. Some events show interesting signals in the Indian and Atlantic oceans, but the behavior is not sufficiently general to be a statistically meaningful element of the composite.
The largest signals in the composite occur in the eastern equatorial and west-central north Pacific and not in the southern hemisphere. Thus, the large scale SLP variations associated with El Niño periods are not dominated by the classical Southern Oscillation. Little evidence is found for phase propagation of the signal in El Niño years. Although several features of the composite occur during the same season during each El Niño period, so that the main signals are "phase locked" to the seasonal cycle, the patterns of variability have little in common with the patterns of the seasonal march of SLP.
The Pacific ocean has several well known modes of seasonal to interannual period variability. In particular, there are times during which tropical South American coastal sea surface temperatures (SSTs) are anomalously warm, others during which central equatorial Pacific SSTs are anomalously high, and others during which there are significant swings in the sea level pressure (SLP) difference between Tahiti and Darwin. While names have been associated with periods of sustained warm coastal SSTs (El Niño) and the Tahiti-minus-Darwin SLP difference (Southern Oscillation), there is no generally accepted language for the periods of warm central equatorial Pacific SSTs. Sometimes periods of central Pacific SST anomaly in excess of 1°C for a season or more are termed equatorial warm events, but this usage is not generally accepted. It is common to speak of El Niño-Southern Oscillation (ENSO) events (e.g., Rasmusson and Wallace, 1983; Philander, 1990), as if this is a single phenomenon that encompasses all three of the above aspects. This awareness of significant connections between the three phenomena came largely from the work of Bjerknes (1966, 1969). Much remains unclear, however, about the extent to which these phenomena arise from a single coupled ocean-atmosphere mode, or from separate physical processes that can occur in different sequences. Deser and Wallace (1987) and others have shown that they are not inevitably linked and do sometimes occur separately. A great deal of work is still underway to examine the evolution, dynamics and predictability of these phenomena, under the programmatic rubric of "TOGA" (tropical ocean-global atmosphere) research.
Both terrestrial and ocean surface data sets have been used to explore the historical characteristics of these TOGA phenomena. Rasmusson and Carpenter (1982, hereafter RC), carried out the seminal modern work using ocean surface data and created a composite of El Niño events between 1946-1976. They provided the first comprehensible basin scale view of SST and wind evolution during these events. Terrestrial time series of rain, wind and SLP have been explored, for example, by Taylor (1973), Gutzler and Harrison (1987), Kiladis and van Loon (1988), and Harrison and Luther (1990) among others. Trenberth (1976), Wright (1984), Barnett (1985), van Loon and Shea (1985, 1987), Trenberth and Shea (1987), Deser and Wallace (1987, 1990), and Wright et al. (1988) have also done important work on the basin scale variability using, variously, wind, SST, SLP and out-going long wave radiation (OLR) data. The preparation of the COADS surface data set (Woodruff et al., 1987) has greatly facilitated basin scale work.
The data collected since 1976 have raised many questions about the utility of the RC composite as subsequent ENSOs have departed from the RC composite in conspicuous ways. The RC composite has motivated so many other studies that advanced our knowledge of TOGA phenomena, however, that we have undertaken to update and extend the composite picture of the ocean surface behavior before, during, and after an El Niño.
We composite over events between 1946 and 1993, and over as much of the ocean surface as can usefully be examined with the COADS data set. We also examine the month to month variability in the regions of substantial signal in order to discuss the degree to which the main features of the composite are representative of the individual events. We find and present here large scale signals in the near-global SLP data. We present our SST and surface wind analyses, and discuss their relationships to SLP variability in a companion paper (Harrison and Larkin, 1996).
The following questions provide the framework for this study:
1) Are the COADS SLP data useful for studies of behavior during El Niño periods? In particular, can we reproduce the low frequency behavior of the Darwin and Tahiti based Troup Southern Oscillation Index using the COADS data, and are there plausible large scale patterns of SLP anomalies? How much smoothing in time and space is needed to bring out the large scale patterns?
2) What is the structure of the composite SLP anomaly (SLPA) during El Niño periods? What statistical significance can we attach to these signals?
3) How representative of the SLPA behavior during individual El Niño events is the composite? Which features are most robust? Least robust?
4) What do our results say about the utility of the composite approach to characterizing SLPA variability during El Niño times? What phenomena do the results identify as deserving of additional study?
Section 2 details the data used and describes the smoothing filters applied in this study. Section 3 compares the traditional Tahiti/Darwin SLP time series and Troup Southern Oscillation Index (SOI) with a Troup-SOI surrogate index using COADS data, to help support the use of COADS for the rest of our study. Section 4 presents the 1946-1993 composite ENSO event. In Section 5 monthly time series are used to examine event-to-event variations. A new ENSO index is proposed. Finally, in Section 6, we review the major results and discuss their implications for ENSO forecasting, diagnosis, and further observation. Due to the many issues of connections between ENSO and the seasonal march, an appendix discussing the average SLP field and climatological seasonal march is provided.
We used two data sets spanning the period 1946-1993 for this study: COADS Release 1 with the 1a standard extension, published by the NOAA Environmental Research Laboratories (Slutz et al., 1985; Woodruff et al., 1987, 1993), and a time series of Darwin SLP, Tahiti SLP, and Troup SOI provided by Dr. Grant Beard of the Australian Bureau of Meteorology. We used the Darwin and Tahiti data to check for consistency with the COADS SLP signals, and used COADS for the bulk of our work. We examined results using both SLP and SLP anomalies (SLPA), defined to be the departure of a particular month from the 1946-1993 monthly climatology. We investigated the effect of using other climatologies, including ones that leave out the ENSO periods, but the major results stay the same; only in periods of small SLPA can the choice of climatology lead to substantially different SLPA patterns.
The limitations of the COADS data for climate studies can be substantial and depend greatly on the variable(s) of interest. We shall not recapitulate the questions that have been raised in previous studies of SST and surface winds, particularly those concerned with identifying multi-decadal trends. Others have found the COADS SLP data to be useful for their studies. Barnett (1985) used COADS SLP for his principal component analysis. Wright et al. (1988), in particular, describe their efforts to scrutinize COADS SLP data. We feel that our SOI "validation" described in Section 3 further supports use of COADS data for this study. On the basis of this, we proceed with further work using the COADS SLP data.
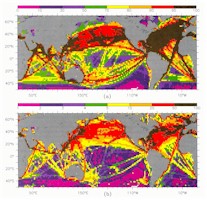
Whenever attempting to evaluate fields of variables from noisy and gappy data sets like COADS, however, the limits of the data distribution should be kept in mind. The data distribution (Figure 1a) shows that shiptracks and data-deficient regions characterize much of the world ocean. The amount of data is much more limited in the southern hemisphere, and the tropics are not well covered. Poleward of 30°S and 60°N there is very little data. The data coverage and the number of observations in each monthly averaged data point also shows substantial variation (Fig. 1b). We have no information regarding the calibration of different barometers, so the underlying "noise" level of our analyses in different regions is not clear.
Fig. 1. The distribution of the 1946-1993 COADS SLP data. a) Percentage of months in which each 2 × 2 degree grid point has data. b) Average number of observations used in calculating each monthly mean COADS SLP data point.
The composite maps presented in this paper are smoothed to highlight the larger scale features by filtering smaller scale temporal and spatial noise. After considerable experimentation, we decided to adopt the smoothing technique used in RC. For our purposes "RC smoothed" is defined as the following procedure: the spatial grid is filled using linear zonal interpolation to define values at points with no data; this is followed by a nine-point (18°) zonal binomial smoother and a seven-point (14°) meridional binomial smoother, after which a 3-month running mean is applied. The zonal smoother has a half power wavelength of 21°; the meridional smoother has a half power wavelength of 18°. Near land the spatial smoothers are reduced to the dimension that will not extend over land. This creates an inconsistency between the near-boundary and mid-ocean smoothing, and boundary gradients will tend to be sharper than mid-ocean gradients due to the reduced smoothing.
Note that this smoothing procedure will not move the location of extrema under most circumstances, but will reduce their amplitudes. Were there better data coverage, so that the smoothing could be reduced, one might find regions of substantially greater gradient than seen here. It is important to note that all of the major features of the composite can be seen clearly in unsmoothed maps. Figure 2a-c shows a typical composite month using various spatial smoothers. More examples of minimally smoothed results are given in Larkin and Harrison (1996).
Fig. 2. The December Year(0) SLPA El Niño composite (see section 4) using different spatial smoothers. a) No spatial smoothing. Note the non-uniform shading intervals, so that variability in the tropics can be seen. b) The same field with gaps filled via linear zonal interpolation, and smoothed via a zonal triangle of ten degree width. c) The same months smoothed by application of the RC smoother (see section 2). All composite results presented hereafter use this latter filling and smoothing.
The standard deviation statistics of this data set deserve some scrutiny and are used in Section 4. Figure 3 shows standard deviations computed over the 1946-1993 period, after the data has been RC-smoothed (above): Fig. 3a of the full (SLP) data set, Fig. 3b of the climatological seasonal march only, and Fig. 3c of SLPA only (climatological monthly means removed). The contour interval is 1 mb with the addition of the 0.5-mb contour to better show the structure of the variability in the tropics.
Fig. 3. Standard deviations of the RC smoothed 1946-1993 monthly COADS SLP data. The contour interval is 1 mb with the addition of the 0.5 mb contour to show structure in the tropics. a) standard deviation of SLP over the entire record. b) standard deviation of the monthly mean SLP climatology. c) standard deviation of SLP anomaly (monthly climatology removed) over the entire record.
The standard deviation of the full data set shows northern hemisphere maxima of 5 to 6 mb off the Aleutian Islands, off of Iceland-Greenland, along the coast near the Persian Gulf, and across the Indian subcontinent continuing on to Korea. The coastal maxima are expected due to the above mentioned smoothing limitations near boundaries. Except off Madagascar, the standard deviation is less than 2 mb until about 20°S. South of 20°S, it increases to a maximum of about 5 mb.
The pattern of the standard deviation of the seasonal march looks very much like that of the full data set north of 10°N. There are very small values (0.5 to 1 mb) over much of the tropics. South of 20°S the values stay small (1 to 2 mb), in contrast to those of the full standard deviation. In the northern hemisphere, the seasonal cycle accounts for a significant amount of the total variability in this monthly mean data set.
The standard deviation of the monthly mean anomalies has a different pattern from either that of the seasonal march or full data set. There is a broad tropical (20°S to 20°N) band of values near unity, and poleward of this the variance is largely an increasing function of latitude to about 4 mb at 50° from the equator. Away from the monsoon areas, the non-seasonal variations are found to be greater than the seasonal variations. In temperate northern hemisphere latitudes the seasonal and non-seasonal variance are similar in magnitude.
The Tahiti and Darwin SLP time series and other derived quantities, particularly the Troup Southern Oscillation Index (SOI), have been widely used in ENSO research because they offer a long-term look at an important measure of the Southern Oscillation. They also offer us a standard against which the COADS SLP data can be compared; were the COADS SLP data unable to reproduce the SOI, it would be difficult to argue for further use of COADS in ENSO studies. In this Section we describe the construction of surrogate "tahiti" and "darwin" time series from COADS, and compare these with the land station data. We have not undertaken a systematic comparison of COADS SLP with other WMO island station SLP records, both because we did not have easy access to the WMO station data set, and because of the larger quality control issues involved in using the WMO data.
To construct the surrogate "tahiti" and "darwin" time series we use the same spatial smoothing (nine-point binomial in longitude, seven-point binomial in latitude, see Section 2) as used to construct the composite, and then pick two points, one near Tahiti and one near Darwin, that are as close to the real stations as possible while making best use of the available data. Our surrogate "tahiti" is chosen as 151°W, 17°S; our surrogate "darwin" as 137°E, 11°S (Tahiti is located at 149.6°W, 17.5°S; Darwin at 130.9°E, 12.4°S).
We find somewhat less variability in the surrogates than in the original time series. The "tahiti" surrogate maximum amplitude is less than Tahiti by about 1 mb, which appears to be the result of area averaging. Averaging over a smaller region yields more similar extreme values, but leads to more gaps in the time series and increased high frequency variability. However, both surrogate series duplicate to a high degree the major low frequency features of the original series. We have examined the anomaly time series as well and find very good correspondence in all of the low frequency features, but differences in high-frequency detail.
A more demanding comparison is how well the surrogate time series can be combined to reproduce the Troup SOI. We calculate a surrogate Troup SOI identically to the way in which the Troup SOI is calculated (McBride and Nicholls, 1983) except using our surrogate "darwin" and tahiti time series. Surrogate COADS Troup SOI = 10* (anomaly of surrogate tahiti minus anomaly of surrogate darwin)/(standard deviation of the record of that calendar month's difference). Figure 4 shows the comparison of the 5-month triangle time-smoothed Troup SOI and the COADS surrogate Troup SOI; correlation statistics on the raw series and time smoothed series are presented in Table 1. The correlations are high, and extremely high when a triangle smoother is applied.
Fig. 4. Troup SOI (solid line) and our COADS "surrogate" of Troup SOI (symbols). Both are shown time smoothed with a 5-month width triangle filter.
TABLE 1. Correlations between Surrogate and Station Time Series
(Graphic image of table)
No time |
5-mo |
13-mo |
|
| Tahiti SLP | 0.94 |
0.98 |
0.96 |
| Darwin SLP | 0.96 |
0.98 |
0.96 |
| Troup SOI | 0.86 |
0.96 |
0.99 |
We have constructed composite maps for the 60-month period spanning January of Year(-2) to December of Year(+2), where Year(0), as in RC, is the year of South American coastal "El Niño" warming. Years(0) are taken to be 1951, 1953, 1957, 1965, 1969, 1972, 1976, 1982, 1987, and 1991. The choices of 1951-1972 match those of RC. We chose 1987 over 1986, as the patterns are more consistent with other ENSO events if we identify 1987 as Year(0) for this event rather than 1986. Using 1986 instead has no significant effect on our composite. The Year(0) choices of 1976, 1982 and 1991 for the other post-1972 ENSOs should not be controversial.
We began our efforts to construct a composite by exploring the effect of normalizing each ENSO event by some maximum amplitude or amplitude difference before averaging events together to form the composite. RC did not perform this normalization, and it has been known for some time that their composite is strongly influenced by the 1972 event, both because of its large amplitude and because more data were available from this event than from the others in their data set. We have been unable to devise a defensible event normalization factor, however, because there are large data gaps spanning the regions of the largest ENSO signals.
A second possible preparation for compositing involves allowing the "zero time" to vary from event to event, since different events seem to have somewhat different phasing relative to the seasonal march. We found no satisfactory strategy for introducing a phase shift; the same data limitations that make it too difficult to define a useful amplitude factor make it even harder to deal with issues of phase. We composite by averaging together the same calendar month of each event, as was done by RC.
The next challenge was to illustrate the features of the global ENSO signal. These features are not easily discerned because the mean SLP field has substantial spatial structure and a significant seasonal march in many areas (see appendix). Examination of ENSO from SLPA fields also presents significant interpretation challenges, since the extra-tropical interannual variability is typically significantly greater than the tropical variability (see section 2). For example, 2 mb in SLPA is a very large tropical signal, but is negligible in middle latitudes. After some exploration, we decided to present the composite in terms of a variance-normalized SLPA. We normalize the RC-smoothed SLPA fields by the standard deviation of the RC-smoothed SLPA time series at each point (see section 2 and Fig. 3c). Contours shown here are in units of regional non-seasonal standard deviation of SLP. We shall denote anomalies normalized in this way as SLPAN, reserving SLPA for unnormalized anomalies (in mb).
This normalization is not traditional for large scale descriptive work, but is similar, although not identical, to normalizations used by van Loon and Shea (1985) and van Loon and Labitzke (1987). We use it here because: 1) it emphasizes the relative importance of the ENSO signal compared to the total non-seasonal variance, 2) this field has little small scale spatial structure of its own (see Fig. 3c), and 3) it facilitates consideration of statistical significance (see below). SLPA composite maps are presented in Larkin and Harrison (1996).
The effect of examining SLPAN instead of SLPA is clearly shown in Fig. 5. The extra-tropical signal is greatly reduced, allowing the tropical signal to stand out. A further benefit of this normalization is that much of what we believe to be statistically insignificant variability poleward of 40°S is filtered out in SLPAN. An unappealing aspect of SLPAN is that it cannot be related simply to wind anomalies. A subsequent paper, Harrison and Larkin (1996), will present wind and SST results and their relation to SLP.
Fig. 5. The effect of normalizing SLPA by Fig. 3c to create SLPAN. Composite September(0) as an example. a) SLPA, contoured every 0.5 mb. b) SLPAN, contoured with zero (heavy line) and then ±0.8, ±1.0, ±1.2, ±1.4, ±1.6, etc... The ±0.8 contours correspond to a local Normal-z 99% significance level. Significance levels of contours are discussed in Section 4.1.
The matter of statistical significance also merits discussion. We check for local (spatial point) significance of the composite using several methods, including the Normal-z statistic, and the Student's t-test (which differ in the standard deviation used). We find comparable results using each method. We shall present the local significance level in terms of the Normal-z statistic as our normalized sea level pressure, SLPAN, and the Normal-z statistic are related by:
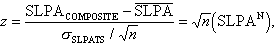
where n is the number of events in the composite (10), and SLPATS is the standard deviation of the RC-smoothed SLPA time series at that point.
However, we note that determination of significance levels in this way is complicated by the lack of data in certain regions and the fact that both the Student's-t and Normal-z statistics assume underlying normal distribution. To address the effect of possible non-normal distributions, we have employed a Bootstrap technique which uses only the data distribution itself (Efron and Tibshirani, 1991) to determine various confidence levels. We apply our Bootstrap method to each spatial point separately, choosing with replacement a time series from the original and then calculating a Bootstrap SLPAN. We used B = 10000 iterations to determine our Bootstrap confidence levels. For confidence intervals up to 99% we find good agreement between the Bootstrap calculations and the Normal-z statistic. This is fortuitous for two reasons: 1) confidence intervals based on z are universal spatially, whereas the Bootstrap intervals are not; 2) the Normal-z statistic is easily related to our normalized sea-level pressure anomaly, SLPAN, as shown above. Hereafter, all mention of local significance levels are to be understood as relating to the Normal-z statistic.
The Normal-z 99% confidence level (the first non-zero contour shown on the composite maps) is SLPAN > z99/(n)0.5 = 0.81. We do not show the 95% confidence level here as little below the 99% level (and much above the 99% level) is found to have field significance. Instead, we refer to the accompanying technical memorandum (Larkin and Harrison, 1996) for presentation of lower local confidence intervals. Note that this is only a test of point significance; for an idealized random distribution we expect 1% of the map to be at or above this level (both positive and negative) on any given composite month. Other levels of SLPAN shown on the composite maps are 1.0 , 1.2, 1.4, and 1.6. While these levels are necessarily above the 99% local confidence level, the exact local significance varies with location on the globe and can only be approximated through the Bootstrap test above. We do not believe that all of the patterns associated with the 99% confidence level are significant in a field (global) sense but find that signals at the 1.0 level and above tend to have enough large scale coherence and temporal stability to be plausible.
Statistically, there are many ways to check for field significance of a given structure in the composite. The simplest is to calculate the percentage of the field in a given month that is locally significant (as above) and then determine the probability that this percentage would be observed randomly (Livezey and Chen, 1983). To do this, some assumption must be made about the spatial interdependence of the field to determine the number of independent spatial points. We have calculated the field significance using a range of assumptions, from an optimistic 21° × 18° (the half power point size of our spatial smoother), to a rather cautious 42° × 36° for each independent point. The local significance criteria checked for field significance can also be varied--a very large scale low level signal (low local confidence level) may still have a high field significance level. We have checked a variety of local significance criteria, from the 50% (zero contour) to the 99.5% levels. Only two components of the composite have field significance at the 95% confidence level in these calculations: the western central north Pacific high (labeled WCNP), and the eastern equatorial Pacific low (EEQ) as will be discussed in the next Section. We note that while we use present results at the 99% local confidence level, we use a 95% confidence level as our field significance criterion. This is due to the fact that our field significance calculation is a stringent test in that it does not take into account the spatial structure, temporal coherence, or other noteworthy characteristics of the signal. More aspects of the composite may be found to be significant using other, tailored tests.
We call signals with field significance at or above 95% "significant" signals. These signals will be shown to be reasonably robust (all or most ENSOs exhibit this behavior). "Marginally significant" signals, ones that have local significance and some spatial and temporal coherence but that do not meet the stringent field significance test above, seem to arise when one or more ENSOs have the sort of behavior found in the composite, or when there is considerable variation in the timing of a particular feature among events. Marginally significant signals occur much more frequently in the composite. We discuss the robustness of our composite results when we examine the event to event behavior in Section 5.
We present selected results of our composite SLPAN analysis in Figs. 6a-o. These selected fields include data from April(-1) through August(-1) and April(0) through May(+1). Please see Larkin and Harrison (1996) for the full July(-2) through June(+2) composite maps. Each smoothed map shown here includes data from a 3-month running mean (section 2), but is referred to by its center month. We show the zero contour and contours of amplitude ±0.8 (99% confidence level), ±1.0, ±1.2, ±1.4, ±1.6. Signals within the 99% interval (-0.8 and 0.8) are not contoured because we judge them unlikely to be significant (see above). Labels are given to features that both meet the 99% local significance level and show some robustness when time series are scrutinized; these features are also discussed in section 5.
Fig. 6. The evolution of the SLPAN El Niño composite, May(-1) through July(-1) and April(0) through April(+1). No significant signals are seen between August(-1) and March(0). Contours are as in Fig. 5(b). SLPAN in excess of ±1 is shaded. See Section 4.2 for discussion of composite features.
The first marginally significant feature (SEAU) is an area of low SLPAN off the southeast coast of Australia in early Year(-1). SEAU appears, nearly fully developed, in May(-1), and intensifies somewhat through July(-1) (Figs. 6a-c). The extreme SLPAN value is nearly -1.2 and occurs over the Tasman Sea in July(-1). While SEAU reaches its extreme value, the greater eastern tropical Pacific SLPAN becomes slightly positive. In a few small regions between 160°W and 130°W, 30°S to 10°S values near +0.8 occur but do not persist. From August(-1) to September(-1) SEAU weakens. While this region continues to have small negative SLPAN, it no longer meets local significance criteria.
Between August(-1) and March(0) there are no other signals of even marginal significance, and these periods are not shown here. During this time, the Pacific north of 30°N remains positive while south of 30°N the Pacific becomes negative. Evidently the composite analysis can contribute little to an understanding of the surface SLPA signals over these months, which are of crucial interest for ENSO forecasting.
In April(0) (Fig. 6d) another marginally significant signal begins: scattered areas from Australia to the Arabian Sea develop positive SLPAN values greater than 0.8. Through June(0), the area northwest of Australia expands around the edges of the continent, and the Arabian Sea signal (ARAB) expands slightly. These signals diminish in July(0) before reaching their maxima in extent and amplitude in August(0). At this point, they connect to form a SLPAN ridge that extends from the Arabian peninsula to Australia, with maximum values greater than 1.0 in many areas and over 1.2 off the Arabian Peninsula (Fig. 6g). The northwest Australian signal has decreased but maxima are seen north of Australia. We group this entire Australian coastal and maritime continent signal as NAUS.
In May(0), just after the start of these positive SLPAN features, a low begins in the eastern Pacific, the first of the field significant features of the composite. This low blossoms in June(0) around two connected centers: to the east on the equator (EEQ) at around 100°W and in the southeastern Pacific (SEP) at (140°W, 30°S). The EEQ low reaches its extreme value in excess of -1.6 in July(0) between 106°W and 84°W, while SEP continues to deepen until August(0), also attaining values below -1.6.
After August(0), the composite signals decline. In September(0) and October(0), the Indian ocean high, ARAB, and the Australian high, NAUS, weaken, and the southeastern low in the tropical Pacific (SEP) decays, leaving the eastern equatorial low (EEQ) as the dominant global signal in October-November(0), with amplitude of -1.2.
In November(0) (Fig. 6j) a new positive signal has formed between 110°E and 180° and roughly 10° to 30°N. This west-central northern Pacific high (WCNP) runs extends from the maritime continent. Meanwhile, low values appear along the North American coast. These two developments herald the start of the second expansion phase of the composite.
WCNP increases substantially in December(0) and continues to grow through January(+1). EEQ, still large in November(0), deepens and spreads, again achieving values below -1.6. Lows are seen all along the west coast of North America, with a substantial low off Alaska (ALSK). In January(+1) (Figure 6m) the ALSK minima is less than -1; the WCNP extremum is greater than 1.4. In addition, there are areas greater than +1.0 all along the north of Australia, extending both east and west (NAUS). Positive anomalies extend east of these highs (WCNP and NAUS) to past the dateline along the two latitude lines 20°N and 30°S. Conversely, negative anomalies extend west of the dateline along the latitudes of the EEQ and ALSK maxima, 0°N and 50°N. This creates a striking pattern in the Pacific, with a pair of highs in the west interwoven with a pair of lows in the east. In February(+1), this pattern begins to fade. The eastern minima and Indo-Australian maxima decay rapidly, leaving the only the WCNP ridge by April(+1) (Fig. 6o). This last remnant decays by May(1). The only Atlantic signal is a small negative region in February(+1) off the Gulf of Mexico.
Figure 7 presents a schematic summary of the composite SLPAN event. The sequence of events is indicated by boreal season, March-May = Sp, June-August = Su, September-November = F, with the year numbers as before. For the winter season, W(-1) = December(-1)-February(0), W(0) = December(0)-February(+1). The only precursive signal is the low off southeastern Australia (SEAU) in Sp, Su(-1). Three seasons later, Sp(0), high anomalies appear around much of northern Australia (NAUS). At the same time (Sp(0)), extreme lows form in the eastern equatorial Pacific (EEQ) and southeastern Pacific (SEP). As the southeastern Pacific low weakens (Su(0)), a high forms in the Indian ocean (ARAB), that is only present during this season. In F(0) the west-central north Pacific (WCNP) high appears; it intensifies and spreads in W(0), the season in which the Alaskan low (ALSK) exists, and in which the northern Australian high (NAUS) and eastern equatorial low (EEQ) weaken. Only the west-central north Pacific (WCNP) high signal lasts into Sp(+1).
Fig. 7. Schematic representation of the major features of the composite, positive (solid line) and negative (broken line), superimposed on the annual mean SLP field. The boreal seasons for each feature are given, with Sp(-1) = March-April-May of Year(-1), etc. Contours are in (SLP - 1000) mb and the contour interval is 2 mb.
This schematic composite usefully summarizes the major features of the full composite, and illustrates that the global ENSO composite signal is not, fundamentally, a southern hemisphere event. In this respect the "Southern Oscillation" aspect of ENSO appears to have been over-emphasized. The northern hemisphere signal is both larger and more robust than the Southern Oscillation aspects of the signal.
TABLE 2. Robustness of Features of the Composite
(Graphic image of table)
Feature |
Seasons (boreal) |
Comments |
|
| SEAU | Low | Sp(-1) - Su(-1) | Dominated by a few early events. Most prevalent pre-1976. |
| NAUS | High | Sp(0) - W(0) | Many events show composite
behavior. Details vary with location and timing. |
| ARAB | High | Sp(0) - F(0) | Most events show composite
behavior. Occurs frequently in non-ENSO periods. |
| EEQ * | Low | Su(0) - W(0) | Very robust. If-and-only-if
relationship with ENSO periods. |
| SEP | Low | Su(0) - F(0) | Many events show composite
behavior. Details vary in location and timing. |
| WCNP * | High | F(0) - Sp(+1) | Most events show composite
behavior. Occurs infrequently in non-ENSO periods. |
| ALSK | Low | W(0) | Not very robust. Dominated by a few events. |
* feature found to be field significant.
We have discussed all of the marginally significant features in this composite, but it is important to recall that only the EEQ and SEP lows and WCNP high features of the composite meet our significance criterion. The centers of these features do not show much zonal or meridional movement during the composite cycle. The EEQ trough forms quickly along the equator, deepens steadily for some months and then remains in place with nearly constant amplitude for several more months, until it shifts southward a few degrees as it weakens. The SEP trough forms in conjunction with EEQ but disappears quickly without moving. The WCNP ridge becomes more zonally oriented as it intensifies but shows little spatial change as it decays in Sp(+1).
To examine the robustness of these major features of our composite (that is, to determine the extent to which this behavior is present in every ENSO event, and only during ENSO events), as well as to see how representative the marginally significant features of the composite are, it is necessary to examine time series of SLPA over regions centered in the areas of these features. We do this in section 5.
Due to the considerable event to event variations, it is not feasible to describe in detail the features of each ENSO event in this data set. Instead, in this section, we show the relationship between aspects of the Schematic Composite and the individual ENSO events. The simplest way to examine the generality of features in the composite is to examine time series of SLPA from regions near the extrema in the composite. We evaluate simple area averages over rectangular regions (10° × 8° in most cases) as close to the extrema as possible. This spatial averaging is comparable to the RC spatial filtering used in the composite. It is not always possible to construct useful time series centered on the extrema, due to data limitations. We experimented with time-filtering the area averages in a variety of ways; the main results are not sensitive to the choice of smoother, provided its half power point lies between three and six months period. Results are presented here using a 5 month triangle smoother. This smoother has a half-power period of 7.6 months and better side-lobe characteristics than the common three running mean (e.g., Chelton and Davis, 1982), which has a half power period of 6.4 months. Figure 8 shows some of the regions over which we evaluated these time series; the coloration indicates the percentage of months having data within the region (as in Fig. 1). In addition, we examined every 10° x 8° region with enough data north of 20°N in the Pacific. Note the paucity of data in the central south Pacific and the western equatorial Pacific regions.
Fig. 8. Location of some of the time series regions used to assess the robustness of the composite, superimposed on December(0) SLPAN. Regions whose time series plots are presented in Section 5 are labeled. Coloration indicates the percentage of months with data as in Fig. 1a.
We present time series normalized by their own standard deviation. This is very similar to the composite normalization, and we use the same notation, with the understanding that, for this section, SLPAN = SLPAREGION AVERAGE /TS. Because the time series regions have slightly different smoothing than the smoothing used in the composite construction, SLPAN values presented here are not identical with composite values at the central location of each region. Results for each region are presented as in Fig. 9. The first two panels present the time series of SLPAN between 1946 and 1994, with ENSO Year(0)s indicated by bottom brackets. This panel helps the reader see if the behavior found during the composite exists during each El Niño period and whether it occurs in other periods. The standard deviation (TS) is written in the upper left hand corner of the first panel, so it may be used to convert SLPAN to SLPA if desired. The third panel presents an overlay of SLPAN for each ENSO period, from Year(-1) to Year(+1). In the following discussion, we use the boreal seasonal notion defined in section 4.3. Recall that the only aspects of the composite that exhibit both local and field significance in excess of the 95% level are the EEQ low and the WCNP high; we consider time series in these regions first.
Fig. 9. The EEQ SLPAN time series averaged over 108°W to 98°W, 4°S to 4°N and time smoothed by a 5-mo triangle filter (see section 5). The top two panels present the time series, 1946-1993. Bottom brackets identify each ENSO Year(0) . The bottom panel presents an overlay of SLPAN for each ENSO period from Year(-1) to Year(+1). The different ENSO events are indicated by number: 1 = 1951, 2 = 1953, 3 = 1957, 4 = 1965, 5 = 1969, 6 = 1972, 7 = 1976, 8 = 1982, 9 = 1987, * = 1991.
Our time series analysis reveals that the most robust pattern found in the composite is the eastern equatorial Pacific low (EEQ) during Sp(0) through W(0) (Fig. 9). We examine the behavior of this feature by averaging from 108°W to 98°W, 4°S to 4°N. Every ENSO period shows one or more negative SLPAN peaks exceeding -1. The major ENSO events, 1957, 1965, 1972, and 1982 each have EEQ < -2 for at least two months. The largest signal was in 1982, when EEQ < -3 was observed. The events of 1965, 1982 and 1991 also had EEQ < -1 during Sp(+1). The 1982 event was the only one in which EEQ < -1 continued past Sp(+1). In non-ENSO periods, EEQ is never < -1 for three consecutive months. Thus EEQ < -1 constitutes a necessary and sufficient criteria for picking out the ENSO periods in this record. The area average can be moved several degrees in any direction without severely altering these results.
While EEQ exhibits a negative peak < -1 during each ENSO period, the characteristics of EEQ vary from event to event. Consider the overlaid ENSO SLPAN (bottom panel of Fig. 9). Typically, EEQ first reaches -1 during the period June-July(0), with 1969 and 1987 occurring significantly earlier and 1991 later. EEQ's behavior during the major ENSO periods can be grouped into two main types. In the first there is a single negative extremum (1953, 1955, 1957, 1972); in the second there are two negative extrema (1951, 1965, 1976, 1982, 1987 and 1991). 1969 is unique in having a broad flat negative extremum, lasting nearly a year.
The next most rigorous connection between a composite feature and individual events is the WCNP high from F(0) into Sp(+1). Figure 10 presents time series for WCNP based on an area average over 158° to 168°E, 20° to 28°N. We see that composite type behavior, with peak values of WCNP > 1, is found in the events of 1951, 1957, 1965, 1972, 1982, 1987, and 1991. Departures from composite behavior are found in the 1953 and 1969 events, which have no positive peak during F(0) - Sp(+1), and in the 1976 event which has weakly negative values during this period. The weakest WCNP maxima occur in the 1951 and 1953 events, with WCNP about 1.5. Most events have maximum WCNP values around 2 and the 1982 event has a maximum WCNP of almost 4. Two non-ENSO periods, 1959 and 1973, have positive extrema above 1.5. Overall, WCNP > 1.5 values are typical of ENSO periods and infrequent during non ENSO periods.
Fig. 10. Same as Fig. 9, except for the WCNP region, 158° to 168°E, 20° to 28N°.
The remaining aspects of the composite--the southeastern Pacific (SEP) low, the northern Australian (NAUS) high, the southeastern Australian (SEAU) low, the Arabian Sea (ARAB) high, and the Alaskan coast (ALSK) low--are of only marginal significance. While they exceed our local significance criteria at the 99% level, they do not meet our stringent field significance test at this level. As might be expected, individual events show more variability for these aspects than they do for EEQ or WCNP. We shall only discuss the SEP and NAUS signals, for reasons mentioned below, but we present SLPAN timeseries averaged over regions representative of the other features: for SEAU (Fig. 11) 150° to 160°E by 42° to 36°S; for ARAB (Fig. 12) 52° to 62°E by 10° to 18°N; for ALSK (Fig. 13) 144° to 134°W by 44° to 52°N.
Fig. 11. Same as Fig. 9, except for the SEAU region, 150° to 160°E, 42° to 36°S.
Fig. 12. Same as Fig. 9, except for the ARAB region, 52° to 62°E, 10° to 18°N.
The SEP low center forms with EEQ in Su(0) but lasts for only two seasons. The SEP composite values greatly exceed the 99% significance level locally, having comparable extrema to EEQ, but SEP is not large enough in area to obtain field significance. We examined the behavior of time series in three different regions near the SEP composite extremum but were limited to areas with the best data coverage. We find the different time series differ non-trivially, suggesting that the data are at best marginal to study this aspect of the composite in detail. Larkin and Harrison (1996) presents the various time series. The only clear results from these series are that the composite SEP signal results substantially from very large values during the 1982 and 1991 El Niño events, and that values in excess of -1.5 occur in about half the El Niño events sometime during Yearr(0) in this general area. Data density is a serious issue for this signal; it is possible that with improved data a more robust result might be found. However, the above results are the strongest permitted by these data.
The NAUS high found in Su, F, W(0), is spatially diffuse in the composite, extending from the Australian coast into the Maritime continent, with extrema occurring in many distinct locations at different times. As a result, it is not surprising that the time series averages reveal that the NAUS high has considerable small scale structure. Location of the areal average severely affects the time series pattern found; for this reason no figure is shown, instead the reader is referred to Larkin and Harrison (1996). The NAUS high results primarily from large signals during the 1972, 1982, and 1991 events; 1987 also exceeds the positive significance threshold, but has weakly declining values throughout these seasons. The remaining events show different characteristics depending upon the region chosen, but frequently have weakly opposite behavior to that found in the composite. Several non-ENSO years show positive values near our significance threshold. The signal in regions off western Australian is typically more robust.
The remaining features of the composite are less spatially diffuse and have better data coverage than SEP and NAUS. Figure 11 reveals that the SEAU negative feature during Sp, Su(-1) results primarily from strong negative extrema during the 1957, 1965, and 1972 ENSOs; 1953 and 1969 also exceed -1 during the time of the negative composite feature. The dominant event is 1957, when the minimum approached -3.75. The 1951 event shows behavior strongly opposite to the composite, while the events of 1976, 1982, 1987 and 1991 either never reach the negative significance level or go weakly positive over the months of interest. Negative values of -1 or less are not uncommon during non-ENSO periods, occurring more than a dozen times. The strongest statement that can be made about SEAU is that it is not uncommon for ENSO events to show this low off Australia in year(-1).
Figure 12 shows the time series (ARAB) of the Arabian Sea high during Sp(0) and Su(0). A maximum exists in this time series during each El Niño period except for the event of 1953, but in several of the events the peak is less than or barely unity. The major contributors to the composite peak are the 1965 and 1987 events, with maxima of about 2. Positive values larger than unity exist during non-El Niño periods of 1968, 78, 79, 83, 84, 86 and 89; the past twenty years exhibit this behavior far more frequently than the first twenty years of our record. Overall we may summarize the robustness of this feature by stating that it is found, to some degree, in almost every El Niño period, but that it also occurs with some frequency during non-El Niño periods.
Figure 13 indicates that the ALSK negative composite feature during season W(0) results primarily from very negative values during the 1957, 1982 and 1991 events. 1953 and 1969 also contribute somewhat to the composite feature, although their extrema occurred more during Su, F(0) than during W(0). 1951, 1972, 1976, 1987 had weakly positive values while the composite was negative. Many non El Niño periods exhibit ALSK < -1.5. This feature is occasionally strongly present during ENSO, but is not truly typical.
Fig. 13. Same as Fig. 9, except for the ALSK region, 144° to 134°W, 44° to 52°N.
It is of interest to examine the time series of the Troup SOI in the format of the composite feature time series (Figure 14). The composite behavior of the Troup SOI is shown in the heavy black line in the third panel; in the spirit of our previous composite discussion we say that low values of SOI between Su(0) and (arguably) Sp(+1) are the composite event feature associated with SOI. The upper panels show that this behavior is not uniquely associated with ENSO periods; the ENSO event periods of 1951 and 1969 do not reach the marginal significance level for composite SOI behavior, two other ENSO periods show very marginal SOI signal (1957, 1976), and the non-ENSO periods of 1946, 1977-78 and 1990 have substantially negative values for at least one season. 1963 and 1993 also show composite type SOI behavior; following the RC convention (as well as that of Deser and Wallace, 1987) 1963 is not an ENSO period, but the status of 1993 has yet to be settled in the literature. In the language we have used for the other composite signals the SOI behavior is relatively robust; all events have SOI < 0 during the period identified by the composite and many have SOI < -1 during this period the composite, but this behavior is not uniquely associated with ENSO periods. The SOI feature is clearly less uniquely associated with ENSO periods than EEQ.
Fig. 14. Same as Fig. 9, except for the Troup SOI, smoothed and normalized as in Figs. 9-13. See section 5.
We used COADS SLP data to examine the climatological seasonal march and ENSO period signals from 1946-1993. Following Rasmusson and Carpenter's (1982) SST and wind study, we constructed a SLP anomaly (SLPA) composite event. We find statistically significant patterns in this composite. These are most easily examined by normalizing the composite SLPA by the standard deviation of the local non-seasonal variability, SLPAN, a variable proportional to the Normal-z statistic. This normalization facilitates the evaluation of significance between tropical and extra-tropical signals, since extra-tropical SLPA variability is much larger than tropical variability.
In our near-global (50°S to 70°N) SLPAN composite, ENSO has statistically significant expression in both hemispheres of the Indian and Pacific Oceans, but none in the Atlantic. The most significant composite signals are found in the northern central and eastern equatorial Pacific. Other less significant Pacific signals occur in the southeastern Pacific, off southern Australia, off northern Australia extending into the Maritime continent, and off the coast of Alaska. In the Indian Ocean, positive anomalies occur everywhere in the north, but are particularly significant in the Arabian Sea off the Arabian Peninsula. We present these features of the composite in section 4 and summarize them schematically in Fig. 7. The composite does not manifest basin scale propagation of the ENSO period signal, particularly during Year(0)-Year(+1). Highs and lows appear, intensify approximately in place, and then diminish. In particular, the Dateline between 15°N and 15°S has very small signals and can be viewed as a node during Year(0).
In order to compare our results with previous work, we review the sequence of the composite event, making reference to previous work as it pertains. May(-1) is the first month to yield a significant signal. It is found off Southeast Australia (SEAU) and continues through June-July(-1) before diminishing. This is the oceanic extension of an Australian SLPA low described by Kiladis and van Loon (1988). They found locally significant lows in land based pressure measurements for the period May-July(-1) and August-October(-1), diminishing in November(-1)-January(0). Our signal is also confined to an area west of the Dateline, as was theirs, but falls below significance by September(-1).
There are no significant signals found in our composite from September(-1) to March(0). Several positive anomalies occur in April(0), brokenly extending from just north of Australia north at about 25°S (NAUS) into the Indian Ocean and the Arabian Sea off the Arabian Peninsula (ARAB). These positive anomalies match with the "peak phase" Indian Ocean signals described by Cadet (1985). These anomalies are followed in May-June(0) by a negative anomaly centered in the eastern equatorial Pacific (EEQ), connected with another center in the southeastern Pacific (SEP). EEQ and SEP are the first extremely strong features of the composite, with SLPAN values below -1.6 in July-August(0). The SEP negative anomaly center disappears by October(0), during which time NAUS weakens. The EEQ anomaly remains strong into Year(+1). NAUS and SEP are the signature of the classical Southern Oscillation pressure swing that has been much studied (Trenberth and Shea, 1987; Kiladis and van Loon, 1988). EEQ is located within an area studied by Wallace et al. (1989) and is similar to a center of low SLP on equatorial SST regression values found by Deser and Wallace (1990).
In November(0), a positive anomaly ridge forms in the west-central north Pacific (WCNP). WCNP intensifies through January(+1), obtaining SLPAN values greater than 1.4 . During this time, a negative anomaly off the Alaskan coast (ALSK) appears for one season only. The EEQ, NAUS, and ALSK anomalies drop below significance by March(+1), leaving only the WCNP high to decay through April(+1). WCNP is similar to strong SLP negative correlation "teleconnectivity" centers found by Wallace and Gutzler (1981) both in SLP, corresponding to the North Pacific Oscillation, and in 500 mb height, corresponding to the related Western Pacific pattern. The opposing centers for both patterns are located near the Dateline but are too far north (>66°N) to be visible in our data. These patterns are distinct from the Pacific/ North American (PNA) pattern whose centers are too far east to match directly either WCNP or ALSK. Wang (1995) also finds a maximum positive SLP signal in March(+1) in a region that encompasses our WCNP region but is much larger. Our composite differs from Wang's analysis in other ways, in that he finds another maximum SLP anomaly to the east of Australia in May(+1) that we do not see, and he does not find any significant SLP signal in our EEQ region. These results are also consistent with van Loon and Labitze (1987) who found in entire western Pacific in the northern Henisphere to be significantly high on average during El Niño periods.
In addition to satisfying a local 95% confidence criteria, we tested each feature of the composite for field significance as per Livezey and Chen (1983) (section 4.1). Only the EEQ and WCNP signals satisfy this stringent field significance test at the 95% level.
To assess the robustness of the features of our composite, we examined time series of the full 1946-1993 record in the vicinity of each feature (section 5). Some aspects occur in the SLP record every time there is an ENSO event, and only when there is an ENSO event. Other aspects do not have such a tight relationship with ENSO, but most aspects occur in the majority of ENSO events. Typically we do not find composite-type behavior during non-ENSO periods. The larger and more intense the signal in the composite, the more robust the signal tends to be. Thus we believe that the composite perspective does offer a useful framework in which to think about the evolution of ENSO events.
We find the EEQ signal to be extremely robust and the WCNP signal to be only slightly less so. Within the NAUS region, there is a positive anomaly in each event, but the location and timing are not consistent from event to event. The SEP negative feature is typically present somewhere in this region of the ocean, but also shows considerable event to event variability. ARAB SLPA typically is significantly positive during ENSO events but is also high during many non-ENSO periods. The SEAU and ALSK features result primarily from large signals in a few events.
Except for the SEAU signal in Year(-1) and the ALSK signal in late(0)-early(+1), the schematic composite features do typify the behavior of SLPA during ENSO. While only the EEQ signal during Year(0) is uniquely associated with ENSO periods (section 5), the other features (except ARAB) occur only infrequently during non-ENSO periods.
The EEQ signal deserves special attention as it is unique to ENSO periods. We find EEQ to be better correlated with central equatorial Pacific SST than any other sea level pressure signal, including the Troup SOI. Wallace et al. (1989), in discussing SST, SLP, and wind connections in the eastern equatorial Pacific, also noted the high negative correlation between SLPA and El Niño South American coastal SST anomalies for a larger region containing EEQ. Their larger area average, however, does not have a unique "if and only if" relationship to ENSO periods. Our analysis also finds that SLPAN values less than -1 in EEQ are a better index for the existence of an ENSO event and the end of an event than are negative values of the SOI. We also suggest that EEQ SLPAN can serve as a useful index for the intensity of ENSO events; 1982 had negative EEQ SLPAN in excess of -2, while other major events typically have maximum values in excess of -1.5; lesser events only just exceed -1. In a companion paper (Harrison and Larkin, 1996), we report a variety of connections between SLPA, SST anomalies, and surface winds associated with ENSO periods and discuss the further issues of classifying ENSO periods and determining the intensity of ENSO events.
Although there are only ten ENSO events between 1946 and 1993, the time series plots (Figs. 9-14) suggest that some of the composite characteristics of ENSO have changed over this period of time. In particular, no event since 1972 has shown a clear, strong, precursive SEAU low, a feature common in the pre-1976 ENSOs. The 1982 ENSO had by far the most substantial signal over EEQ and ALSK of any event in the record. Also in the 1982 and 1991 events, more signal persists into Year(+1) than in other events. Although the composite shows no Atlantic signal, several of the post-1972 events have had substantial equatorial Atlantic expression, but these have not been strong enough to over-balance the opposite behavior found in other events (see Larkin and Harrison, 1996, for time series in this region). It is important to note that none of these aspects can be accorded any statistical significance on the basis of this data set. The statistical stationarity of the major features of ENSO deserves further study, data permitting.
A surprising aspect of the composite is the extent to which the most robust aspects of the composite SLPAN ENSO life-cycle occur near the equator and in the northern hemisphere. The northern hemisphere expression of ENSO is both more intense, relative to its total variability, and more consistent from ENSO to ENSO event than is the southern hemisphere signal. Other work has also suggested that the northern hemisphere SLP ENSO signal is greater than the southern hemisphere (e.g., Barnett, 1985). However, our composite results differ from Barnett's empirical orthogonal function analysis results in several respects. We find no evidence for eastward propagation of the signal across the Pacific (a prominent feature of his analysis), and our maximum northern Pacific signal is in a different location. Our eastern equatorial Pacific signal is much more significant than suggested by Barnett.
The southern hemisphere SLPA anomalies during ENSO periods have previously received considerable attention, due to the availability of island SLP data. Historically, descriptions have focused on large scale pressure swings between the western Pacific near Australia and the eastern Pacific near Tahiti that have been correlated with El Niño events (e.g., Rasmusson and Carpenter, 1982). This Southern Oscillation aspect of the SLPA signal deserves discussion. The Southern Oscillation's east-west negative swing is included in the composite through the rise in SLP in the NAUS region and the decrease of SLP in SEP. The details of these features, however, appear different from previous studies, notably Trenberth and Shea (1987). In particular, we see confinement of the southern-hemisphere negative signals to EEQ and SEP, and we do not pick out this pressure swing as the dominant SLPA feature of ENSO periods. Such comparison is complicated somewhat by the fact that previous works have examined this variability with different time filters.
Trenberth and Shea (1987) define the Southern Oscillation to involve SLPA patterns on time scales long compared to those being examined here. Their study of the patterns and evolution of the Southern Oscillation uses an 11-point low pass filter with a half-power period of 20 months, effectively filtering out all energy on periods shorter than one year. They chose this long time filtering in order to seek smoothly time varying basin scale patterns for coherence analysis. None of the features in our composite last for more than a year, and most last for only three seasons. Thus Trenberth and Shea confined their interest to phenomena different from those identified by our compositing strategy. The very large spatial scale patterns identified in their study of the Southern Oscillation have counterparts in the basin scale background patterns of our composite. We have redone our composite analysis, using the RC space smoothing used here, but with the time-filter used by Trenberth and Shea (defined in Trenberth, 1984) instead of the RC three month running mean. When results are presented in SLPAN, again at the 99% confidence interval and above, but appropriately adjusted for the change in standard deviations (Larkin and Harrison, 1996), we find that the EEQ and WCNP signals remain robust and are still the most intense signals, while the NAUS signal is more spatially coherent and the ALSK signal disappears. ARAB remains virtually unchanged. The biggest change is seen in the SEAU signal, which shows increased persistence and expands to the southwest, now matching up with an SLPA low found by van Loon and Shea (1987) during this same period. At the end of Year(-1) and in early Year(0), SEAU, under the Trenberth and Shea filter, extends eastward, seeming to link the SEAU Year(-1) signal with the SEP Year(0) signal, as was found by van Loon and Shea (1987). This transition signal does not meet our field significance criteria, however.
The other time filtering method is typified by Deser and Wallace (1987) who define the Southern Oscillation to be "the seesaw in surface pressure anomalies between the Indian Ocean-Australian region and the southeastern tropical Pacific on seasonal time scales" (p. 14,189) and only smooth with seasonal filters. Relative to this usage, it is appropriate to speak of the composite SLP patterns we identify as the "evolution" of the southern oscillation during the 1946-1993 ENSO periods. This usage is not consistent with that used in Trenberth and Shea (1987), however. Our re-analysis, using the Trenberth and Shea filter, shows that the details of the composite are altered when greater time smoothing is introduced, but that the WCNP and EEQ signals remain dominant. However one describes them, there are substantial SLP signals that form and decay during ENSO periods in each hemisphere. Any dynamic model of the ocean-atmosphere interaction during an ENSO event needs to account for the more localized northern signals and their higher frequency components as well as the smaller, broader scale and lower frequency signals of Trenberth and Shea's study.
There has been considerable speculation about the nature of the connections between ENSO and the seasonal march in recent years. Philander (1990, chapter 6) and others have remarked upon similarities between the seasonal march and aspects of the RC SST composite, and there has been speculation that perhaps the initial phases of ENSO can be viewed as an enhancement of the seasonal march. Comparison of our composite with the climatological seasonal march over the same period (see appendix) shows no substantial similarity either in the patterns or progression throughout the year. Aspects of our composite do occur during the same period in all of the individual events in our record. Thus there is a strong connection (phase locking) between the seasonal cycle and our ENSO variability, but the variability does not resemble the evolution of the seasonal march. Overall, the ENSO patterns of variation appear so unlike the patterns of the seasonal march as to suggest that the phenomena responsible for ENSO are distinct from those responsible for the seasonal march. Recent work (e.g., Wang, 1995) has speculated how two phenomena as dissimilar as the seasonal cycle and ENSO seem to be, could be "phase locked." The relationship (or lack thereof) between ENSO processes and the seasonal march deserves further study.
The composite view of ENSO cannot convey the many interesting details of individual ENSO events, but we believe that it describes sufficient commonality to be useful. Several aspects of the composite merit further study. In particular, what are the atmospheric or coupled ocean-atmosphere processes that lead to the shift from a southern-hemisphere/ equatorial pattern in mid YR(0) to an eastern equatorial/ western north Pacific pattern in early Year(+1)? Why is the Dateline nearly a node for ENSO atmospheric mass redistribution, and how are the various other aspects of this redistribution brought about? How do we rationalize the seeming absence of phase propagation of SLPA signal with the present coupled oscillator models of ENSO?
We believe that this composite perspective, and its robustness, provides a useful tool for identifying significant ENSO period signals. We hope that it can help provide a framework to focus thinking about basic coupled ocean-atmosphere processes and interannual variability, and will be pleased if this paper, and its companion on SST and surface wind (Harrison and Larkin, 1996), provides a fraction of the stimulation offered by Rasmusson and Carpenter (1982).
Acknowledgements. This work was done as part of the Thermal Modeling and Analysis Project (TMAP) at PMEL. TMAP research is supported through funding: to the NOAA/UW Hayes Center for the Study of Seasonal to Interannual Variability by NOAA's Office of Global Programs and ERL headquarters; by the NASA Mission to Planet Earth Physical Oceanography Program (NASA Interagency Agreement #W-18,242); and through funding from Dr. Eddie Bernard, Director, PMEL. Mr. Larkin is supported through an NDSEG fellowship. We thank Grant Beard from the Bureau of Meteorology, Australia, for the Tahiti SLP, Darwin SLP, and Troup SOI monthly data, and NOAA CDC for maintaining the COADS data. This work was analyzed using the FERRET data visualization program, created and freely distributed by Steve Hankin of TMAP (http://www.pmel.noaa.gov/ferret/home.html). Jerry Davison and Kevin O'Brien, TMAP staff, assisted in many ways. Finally, Ed Sarachik, Mike Wallace, Gene Rasmusson, and George Philander deserve special mention for years of stimulating discussion about El Niño, the Southern Oscillation, and other phenomena of tropical ocean/atmosphere interaction. This is PMEL Contribution Number 1647 and NOAA/ Hayes Center publication Number 359.
Appendix
The Annual Mean and Climatological Seasonal March
A brief review of the global SLP field and its seasonal march is given here as a reference for discussion of the ENSO signals. Although many of these results are known to meteorologists, they are less so to oceanographers, and we offer a somewhat different presentation of the climatological march than we have seen elsewhere.
Figure A.1 presents the RC-smoothed (see section 2 for definition) annual mean SLP and surface wind fields. Although our focus here is on SLP and its variability, because the wind tends to flow down-gradient near the equator and roughly along isobars further poleward, including the wind field may help the reader to visualize the impact of SLP variations. The major SLP features are familiar: subtropical highs in each ocean in each hemisphere with maxima (of about 1020 mb) near 32° latitude and subpolar lows in the North Atlantic and Pacific with minima (of about 1006 mb) near 60° and 55°N, respectively. There is also a second subtropical maximum (of about 1019 mb) in the northern hemisphere just at the Asian coast near 38°N. The southern hemisphere poleward of its subtropical maxima has diminishing SLP values down to 50°S, which is as far south as we feel it is defensible to present COADS SLP results.
Fig. A1. The annual average SLP and wind fields, RC smoothed. SLP is shown as (SLP - 1000) mb with a contour interval of 1 mb. The annual average wind field is superimposed (scale as indicated).
The tropical patterns differ considerably from ocean to ocean. The Pacific has an equatorial minimum near 160°E, with SLP increasing eastward to about 110°W (about 3 mb total increase) followed by a slight decrease to the South American coast (80°W), and increasing westward all the way across the Indian ocean to the African coast (about 3 mb total increase) from the minimum. The equatorial Atlantic has very little SLP gradient, being everywhere between 1012 and 1013 mb, but with the highest value near its center.
Two other features of the mean merit note. The northern hemisphere Indian ocean is unique, in that it has little meridional SLP gradient; thus it lacks the northeasterly trades present in the Atlantic and Pacific. The northeasterly trades are present in the Indian Ocean during the winter months, but are cancelled out by the southwest monson in the annual mean. The zonal extent of the subtropical highs is about 100° of longitude in every basin, which leaves the western South Pacific with a weak saddle along 35°S between 160°E and 150°W.
The seasonal march is presented as monthly mean departures from the annual mean in Figs. A.2.a-f. There is considerable structure to the seasonal march, so we do not attempt to represent it simply by the amplitude and phase of the annual harmonic. Despite the length of the following description, we believe it useful to look at the seasonal march in some detail, particularly because there is still much uncertainty about the extent to which ENSO can be thought of usefully as an enhancement or modification of the seasonal march. The surface wind seasonal march departures are overlaid, as for the mean.
Fig. A2. The SLP and wind monthly climatology departure from their annual means, RC smoothed. The SLP departure in mb, positive (heavy line) and negative (light line). The wind departure with scale as indicated.
We begin with November, the month which is most similar to the annual mean (Fig. A.2.a). The largest departures are in the Pacific. There is an Asian high, 6 mb higher than the mean near the coast, diminishing to zero about the Dateline. From about 30°N to the equator, predominantly NNE wind departures are associated with this feature. The northern Indian Ocean is also positive, with largely NE wind departures. The North Pacific north of about 40°N is anomalously low (-6 mb in the Gulf of Alaska), resulting in westerly wind departures. The Atlantic is within 2 mb of the annual mean between 40°S and 60°N.
In December the Asian and Indian positive departures increase, and the North Atlantic and North Pacific negative departures deepen and extend further toward the tropics. Positive departures form around the US and Central America, but do not extend as far as the equator. The entire South Indian, and almost all of the South Pacific, show negative departures with the maximum values near Australia. The South Atlantic continues to have very weak departures except near the Argentine coast.
In January and February the December pattern has intensified. The biggest changes are tropical negative departures between the equator and 20°S from the east African coast to about the Dateline, with substantial northwesterly winds. The northern hemisphere negative departures are at their most intense (-10 mb at 40°N, 160°W; -7 mb just SE of Greenland). In February, positive departures and easterly wind anomalies appear south of 35°S in the Indian and Pacific basins.
In March there is a major pattern shift to a zonally banded structure for the SLP departures: negative north of about 35°N; positive between about 25° and 5°N; negative south of 5°N to about 35°S and then positive further south. The North Pacific low is greatly reduced in strength. There continues to be a positive extremum at the Chinese coast which diminishes eastward. For the first time in the seasonal march, the strongest wind anomalies are tropical and are found in all three basins.
There is an abrupt change in many of the departure patterns in April, and generally the departures are weaker than previously in both hemispheres. The Indian Ocean has little signal north of about 30°S, the South Pacific has little signal and the North Pacific now has positive anomalies everywhere with a high centered near (40°N, 180°). The North Atlantic anomaly is now positive north of about 40°N and the remainder of the Atlantic has small SLP anomalies. As in March, the largest wind anomalies are tropical. But now they are entirely associated with the Intertropical Convergence Zones of the Atlantic and Pacific.
Were the seasonal march to be completely symmetric, the anomalies of the remaining 6 months would simply be the opposite of November through April. It will suffice to complete this description of the seasonal march by pointing out the differences from this inverse pattern.
In May these differences include a zonal band of positive departure north of 50°N in the Atlantic (6 mb max vs -3 mb max) and a coherent SE Pacific negative departure south of 20°S and east of about 150°W. In June the departures are primarily south of 30°S in the South Pacific and the the SE Indian (about -6 mb vs 2 mb maxima). In July they are in the Atlantic between the equator and about 20°N (positive, about 2 mb max in both July and Jan.) In August the North Atlantic pattern is similar but weaker (3 mb vs -6 mb). In September the North Atlantic stays negative north of about 55°N, instead of becoming positive, and the Southern hemisphere south of 30°S is less consistently negative than would be implied from March; this may well be just a lack of data at the end of Austral winter. October has a three cell pattern in the North Pacific instead of a single cell in April; the largest changes are that there continues to be high pressure in the NW Pacific (still 4 mb maximum) and a minimum in and south of the Gulf of Alaska.
Barnett, T.P., 1985: Variations in near-global sea level pressure. J. Atmos. Sci., 42, 478-501.
Bjerknes, J., 1966: A possible response of the atmospheric Hadley circulation to equatorial anomalies of ocean temperature. Tellus, 18, 820-829
_____, 1969: Atmospheric teleconnections from the equatorial Pacific. Mon. Wea. Rev., 97, 163-172.
Cadet, D.L., 1985: The Southern Oscillation over the Indian Ocean. J. Climatol., 5, 189-212.
Chelton, D.B., and R.E. Davis. 1982: Monthly mean sea-level variability along the west coast of North America. J. Phys. Oceanogr., 12, 757-783.
Deser, C., and J.M. Wallace, 1987: El Niño events and their relationship to the Southern Oscillation: 1925-1986. J. Geophys. Res., 92, 14 189-14 196.
_____, and J.M. Wallace, 1990: Large-scale atmospheric circulation features of warm and cold episodes in the tropical Pacific. J. Climate, 3, 1254-1280.
Efron, B. and R. Tibshirani, 1991: Statistical data analysis in the computer age. Science, 253, 390-395.
Gutzler, D.S., and D.E.Harrison, 1987: The structure and evolution of seasonal wind anomalies over the near-equatorial eastern Indian and western Pacific oceans. Monthly Wea. Rev., 115, 169-192.
Harrison, D.E., and D.S. Luther, 1990: Surface winds from tropical Pacific islands--climatological statistics. J. Clim., 3, 251-271.
_____, and N.K. Larkin, 1996: The near-global COADS SST and surface wind signal: El Niño composite and time series results, 1946-1993. Rev. Geophys., in press.
Kiladis, G.N. and H. van Loon, 1988: The Southern Oscillation. Part VII: Meteorological anomalies over the Indian and Pacific sectors associated with the extremes of the oscillation. Mon. Wea. Rev., 116, 120-136.
Larkin, N.K. and D.E. Harrison, 1996: An atlas of the COADS sea-level pressure signal: A near-global El Niño composite and time series, 1946-1993. NOAA Tech. Memo., in press.
Livezey, R.E. and W.Y. Chen, 1983: Statistical field significance and its determination by Monte Carlo techniques. Mon. Wea. Rev., 111, 46-59.
McBride, J.L. and N. Nicholls, 1983: Seasonal relationships between Australian rainfall and the Southern Oscillation. Mon. Wea. Rev., 111, 1998-2004.
Philander, S.G., 1990: El Niño, La Nina, and the Southern Oscillation. Academic Press, 293pp.
Rasmusson, E.M. and T.H. Carpenter, 1982: Variation in tropical sea surface temperature and surface wind fields associated with the Southern Oscillation/ El Niño. Mon. Wea. Rev., 110, 354-384.
_____, and J.M. Wallace, 1983: Meteorological aspects of the El Niño/ Southern Oscillation. Science, 2, 220, 1195-1202.
Slutz, R.J., S.J. Lubker, J.D. Hiscox, S.D. Woodruff, R.L. Jenne, D.H. Joseph,
P.M. Steuer, J.D. Elms, 1985: Comprehensive Ocean-Atmosphere Data Set: Release
1.
NOAA Environmental Research Laboratory, Boulder, CO, 268 pp.
Taylor, R.C. 1973: An Atlas of Pacific Islands Rainfall. Hawaii Institute of Geophysics data report, HIG-73-9. Univ. of Hawaii, Honolulu, HI.
Trenberth, K.E., 1976: Spatial and temporal variations of the Southern Oscillation. Quart J. Roy. Meteor. Soc., 102, 639-653
_____, 1984: Signal versus noise in the Southern Oscillation. Mon. Wea. Rev., 112, 326-332
_____, and D. Shea, 1987: On the evolution of the Southern Oscillation. Mon. Wea. Rev., 115, 3078-3096.
van Loon, H. and Labitzke, 1987: The Southern Oscillation. Part V: The anomalies in the lower stratosphere of the northern hemisphere in the winter and a comparison with the Quasi-Biennial Oscillation. Mon. Wea. Rev., 115, 357-369.
_____, and D.J. Shea, 1985: The Southern Oscillation. Part IV: The precursors south of 15S to the extremes of the oscillation. Mon. Wea. Rev., 113, 2063-2074.
_____, and D.J. Shea, 1987: The Southern Oscillation. Part VI: Anomalies of sea level pressure on the southern hemisphere and of Pacific sea surface temperature during the development of a warm event. Mon. Wea. Rev., 115, 370-379.
Wallace, J.M. and D.S. Gutzler, 1981: Teleconnections in the geopotential height field during the northern hemisphere winter. Mon. Wea. Rev., 109, 784-812.
_____, T.P. Mitchell, and C. Deser, 1989: The influence of sea-surface temperature on surface wind in the eastern equatorial Pacific: Seasonal and interannual variability. J. Climate, 12, 1492-1499.
Wang, B., 1995: Transition from a cold to a warn State of the El Niño-Southern Oscillation cycle. Meteorol. Atmos. Phys. 56, 17-32
Woodruff, S.D., R.J. Slutz, R.L. Jenne, and P.M. Steurer, 1987: A comprehensive ocean-atmosphere data set. Bull. Amer. Meteor. Soc., 68, 1239-1250.
_____, S.J. Lubker, K. Wolter, S.J. Worley, and J.D. Elms, 1993: Comprehensive Ocean-Atmosphere Data Set (COADS) Release 1a: 1980-92. Earth System Monitor, 4, 1-8.
Wright, P.B., 1984: Relationships between indices of the Southern Oscillation, Mon. Wea. Rev., 112, 1913-1919.
_____, J.M. Wallace, T.P. Mitchell and C. Deser, 1988: Correlation structure of the El Niño/Southern Oscillation phenomenon. J. Climate, 1, 609-625.
Return to Abstract