 Myr), for five spreading rate bins (equivalent to the magmatic budget bins in Figure 5a) as
Myr), for five spreading rate bins (equivalent to the magmatic budget bins in Figure 5a) as
U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
While we have hydrothermally surveyed, to some degree, about 20% of the global ridge system (Figure 1b), only 13 ridge sections totaling half that distance (Figure 5) are suitable for examining the magmatic budget hypothesis described in the Introduction. These sections span the entire global spectrum of the ridge magmatic budget (as calculated from spreading rates), however, and describe a consistent and robust relationship. The first-order trend in plots of Vm vs. both ph and Fs is a decline in hydrothermal activity with decreasing magma budget, though inconsistencies occur in each plot as well. In the ph plot (Figure 5b), most of the data points (ignoring the heavily biased Gakkel Ridge data and the hotspot-affected ridges) define a robust trend with a least-squares regression of
ph = 0.043 + 0.00055Vm
with r2 = 0.93. This result agrees with earlier predictions [Baker and Hammond, 1992; Baker et al., 1996].
Considerably more scatter exists in the Fs plot (Figure 5a). We interpret this scatter as a function of three overlapping uncertainties: increasing difficulty in defining the boundaries of discrete vent fields as spreading rate increases, wide variability in the effort expended in finding discrete vent sites on different ridge sections, and pronounced differences in the length of surveyed ridge sections (Table 1). After binning these data to mitigate these uncertainties as far as presently possible, the resultant least-squares regression is
Fs = 1.0 + 0.0023Vm
with r2 = 0.97.
These robust linear relations offer sturdy support for the hypothesis that crustal magmatic budget is the primary influence on the large-scale (multisegment) distribution of hydrothermal activity. The fact that the activity on ultraslow ridges is appreciably greater than zero, especially considering that we may have conservatively overestimated the true melt supply at the sampled ridges, suggests that ultraslow ridges may in fact be more efficient producers of vent fields than other ridges. We can test this idea by normalizing Fs to the time-averaged delivery of magma [Baker et al., 2004]. To normalize Fs, we calculate Fm, sites/(1000 km Myr), for five spreading rate bins (equivalent to the magmatic budget bins in Figure 5a) as
Myr), for five spreading rate bins (equivalent to the magmatic budget bins in Figure 5a) as
Fm = 10 N/(LusTc)
N/(LusTc)
where for each bin N is the number of vent fields observed, L is the total ridge length (km), us is the weighted average full spreading rate (mm/yr), and Tc is the nominal crustal thickness of 4 km for ultraslow ridges and 6.3 km for all other ridges [White et al., 1992, 2001] (Table 1). Fm for ultraslow ridges are minimum values considering that sections of these ridges (especially where the spreading rate <12 mm/yr) may actually have near-zero crustal thickness [Dick et al., 2003]. Fm steadily increases from superfast to slow ridges then increases sharply for ultraslow ridges (Figure 7). For a given magmatic budget, ultraslow ridges appear 2–4 times as efficient as fast-spreading ridges in creating vent fields. The trend of increasing Fm with decreasing us is consistent with the expected addition of heat from sources other than crustal cooling of basaltic magma at slow and ultraslow ridges. We caution again, though, that data from slow ridges is uncomfortably scarce.
Figure 7. Site frequency Fs normalized to the magma delivery rate vs. spreading rate for the binned data in Figure 5a. Solid circles indicate mean values, open circles the uncertainty range (see Figure 5a). Approximately same trend would result using the ph data in Figure 5b (excluding the biased Gakkel Ridge result and the hotspot-affected ridge sections).
Additional work on slow and ultraslow ridges will be required to establish whether the apparent trend between Fm and us can be verified. In particular, the data for slow (20–55 mm/yr) ridges are so limited that our calculated Fm is speculative. If this trend is confirmed by future surveys, it will indicate that as spreading rates decrease the incidence of hydrothermal activity can be increased by factors other than the long-term magmatic budget. These may include an increased bulk permeability effected by the penetration of deep and enduring faults, strongly three-dimensional magma delivery, and additional heat sources such as direct cooling of the upper mantle, cooling gabbroic intrusions, and serpentinization.
Despite the robust trends in Figure 5, it is important to remember that these results do not demand that the fluxes of hydrothermal heat or chemicals are also similarly related to the magmatic budget. Many additional quantitative flux measurements, at a variety of spreading rates, will be needed to confirm that inference.
The global trend established in Figure 5a can also be used to estimate the total number of vent fields presently active on the ridge system. If we recast the binned data in Figure 5a as a plot of Fs vs. us, the least-squares regression is
Fs = 0.88 + 0.015us.
Applying this relation to the global distribution of ridge spreading rates binned at 20 mm/yr intervals yields a histogram of predicted vent sites with a total population of 1060 (with 95% confidence limits of 992–1153) (Figure 8). In contrast to the dominance of slow-spreading ridges in the global distribution of spreading rates (Figure 2c), vent field populations differ by only about a factor of 2 across spreading rate categories, except in the 100–140 mm/yr bins where total ridge length is <2% of the global sum.
Figure 8. (a) Histogram of predicted vent site population as a function of spreading rate in 20 mm/yr bins (e.g., 0–20, 20–40, etc.). Total population on ridges is estimated as 1060. (b) and (c) show 95% confidence limits for high and low estimates, respectively.
A recurring concern in attempting to relate hydrothermal activity to geological variability is that hydrothermal data are unavoidably time aliased. Mean hydrothermal activity over a much longer period might be distributed quite differently than at present, especially at slow spreading rates. This problem can be partially addressed by comparing the vent field distribution with the oceanic distribution of  He, an unequivocal and conservative tracer of magmatic degassing along ridge crests [Craig and Lupton, 1981]. Overlaying the global ridge system with the deep-water (2000–3000 m) (
He, an unequivocal and conservative tracer of magmatic degassing along ridge crests [Craig and Lupton, 1981]. Overlaying the global ridge system with the deep-water (2000–3000 m) (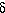
 He%) pattern [Geosecs Atlantic, Pacific, and Indian Ocean Expeditions, 1987; Jamous et al., 1992; Lupton, 1995, 1998; Rüth et al., 2000] reveals a strong, but not perfect, correlation between us and
He%) pattern [Geosecs Atlantic, Pacific, and Indian Ocean Expeditions, 1987; Jamous et al., 1992; Lupton, 1995, 1998; Rüth et al., 2000] reveals a strong, but not perfect, correlation between us and 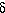 (
( He%) (Figure 9). The most intense
He%) (Figure 9). The most intense 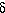 (
( He%) plume in the ocean spreads westward from the fastest spreading ridge segments in the ocean, and other intense plumes originate on the fast-spreading northern EPR and the intermediate-rate JDFR. The Atlantic has lower
He%) plume in the ocean spreads westward from the fastest spreading ridge segments in the ocean, and other intense plumes originate on the fast-spreading northern EPR and the intermediate-rate JDFR. The Atlantic has lower 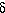 (
( He%) than either the Pacific or Indian Oceans [Geosecs Atlantic, Pacific, and Indian Ocean Expeditions, 1987; Rüth et al., 2000]. This general pattern suggests that we have not grossly misrepresented the differences in hydrothermal activity between fast- and slow-spreading ridges, and demonstrates that this relation holds over at least the last ~10
He%) than either the Pacific or Indian Oceans [Geosecs Atlantic, Pacific, and Indian Ocean Expeditions, 1987; Rüth et al., 2000]. This general pattern suggests that we have not grossly misrepresented the differences in hydrothermal activity between fast- and slow-spreading ridges, and demonstrates that this relation holds over at least the last ~10 yr. This timescale is equivalent to both the turnover time of the oceans’ thermohaline circulation and, coincidentally, the time for a water volume equal to the global ocean to be cycled through hydrothermal plumes [Kadko et al., 1995; German et al., preprint, 2004].
yr. This timescale is equivalent to both the turnover time of the oceans’ thermohaline circulation and, coincidentally, the time for a water volume equal to the global ocean to be cycled through hydrothermal plumes [Kadko et al., 1995; German et al., preprint, 2004].
Past this basic distinction between fast and slow ridges in Figure 9, the distribution of 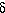 (
( He%) becomes more complex. Values of
He%) becomes more complex. Values of 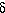 (
( He%) along fast-spreading ridges in the eastern Pacific show discrete highs rather than a uniform distribution corresponding to the spreading rate trend. Unexpectedly low
He%) along fast-spreading ridges in the eastern Pacific show discrete highs rather than a uniform distribution corresponding to the spreading rate trend. Unexpectedly low 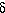 (
( He%) values occur all along the ridge from the Indian Ocean triple junction to the EPR-Chile Rise triple junction. These features are not solely the result of long-wavelength fluctuations in the distribution of vent fields, but instead may be generated by patterns of oceanographic advection and ventilation. Deep currents in the eastern Pacific and vigorous vertical and circumpolar mixing around Antarctica are two primary controls on the
He%) values occur all along the ridge from the Indian Ocean triple junction to the EPR-Chile Rise triple junction. These features are not solely the result of long-wavelength fluctuations in the distribution of vent fields, but instead may be generated by patterns of oceanographic advection and ventilation. Deep currents in the eastern Pacific and vigorous vertical and circumpolar mixing around Antarctica are two primary controls on the 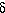 (
( He%) distribution [Farley et al., 1995; Lupton, 1998]. These complications, in fact, emphasize the value of more complete knowledge about the global distribution of vent fields. Without accurate knowledge of
He%) distribution [Farley et al., 1995; Lupton, 1998]. These complications, in fact, emphasize the value of more complete knowledge about the global distribution of vent fields. Without accurate knowledge of  He sources along the global ridge system, the utility of
He sources along the global ridge system, the utility of 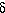 (
( He%) distributions as a tracer of ocean advection and mixing will remain limited.
He%) distributions as a tracer of ocean advection and mixing will remain limited.
Figure 9. Deep-water (~2000–3000 m) distribution of 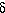 (
( He)% values [Geosecs Atlantic, Pacific, and Indian Ocean Expeditions, 1987; Lupton, 1995, 1998; Jamous et al., 1992; Rüth et al., 2000] compared to ridge full spreading rates (
He)% values [Geosecs Atlantic, Pacific, and Indian Ocean Expeditions, 1987; Lupton, 1995, 1998; Jamous et al., 1992; Rüth et al., 2000] compared to ridge full spreading rates (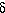 (
( He)% = 100(R/R
He)% = 100(R/R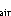 – 1); R =
– 1); R =  He/
He/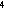 He). Areas with
He). Areas with 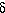 (
( He)% values >30 are shaded. The MOR is divided into four rate categories corresponding to increasing line thickness: 1, <20 mm/yr; 2, 20–<50 mm/yr; 3, 50–100 mm/yr; 4, >100 mm/yr.
He)% values >30 are shaded. The MOR is divided into four rate categories corresponding to increasing line thickness: 1, <20 mm/yr; 2, 20–<50 mm/yr; 3, 50–100 mm/yr; 4, >100 mm/yr.
Return to previous section or go to next section