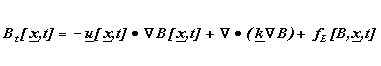 (1)
(1)
ABSTRACT
Individual-Based Modeling (IBM) techniques offer many advantages for
spatially explicit modeling of marine fish early life history. However,
computationally efficient methods are needed for incorporating spatially
explicit circulation and prey dynamics into IBM's. Models of Nutrient-Phytoplankton-Zooplankton
(NPZ) dynamics have traditionally been formulated in an Eulerian (fixed
spatial grid) framework, as opposed to the pseudo-Lagrangian (individual-following)
framework of some IBMs. We describe our recent linkage of three models
for the western Gulf of Alaska: 1) a three-dimensional, eddy-resolving,
wind- and runoff-driven circulation model, 2) a probabilistic IBM of growth
and mortality for egg and larval stages of walleye pollock (Theragra
chalcogramma), and 3) an Eulerian, stage-structured NPZ model which
includes production of larval pollock prey items. Individual fish in the
IBM are tracked through space using daily velocity fields generated from
the hydrodynamic model, along with self-directed vertical migrations of
pollock appropriate to each life stage. The NPZ dynamics are driven by
the same velocity, temperature and salinity fields as the pollock IBM,
and provide spatially and temporally varying prey fields to that model.
The resulting prey fields yield greater variance of individual attributes
(e.g. length), relative to models with spatially uniform prey. Practical
issues addressed include the proper time filtering and storage of circulation
model output for subsequent use by biological models, and use of different
spatial grids for physical and biological dynamics. We demonstrate the
feasibility and computational costs of our coupled approach using specific
examples from the western Gulf of Alaska.
1. Introduction
Modern fisheries research continues to establish important linkages among fish populations, their prey and predators, and characteristics of the immediate physical environment (e.g. circulation, temperature). As interactions among populations and the environment are clarified by field measurement and laboratory experiment, there is a growing need for fisheries models that simultaneously include several trophic levels and specific populations. A single modeling approach may not serve well for all trophic levels and populations, however.
At present the majority of marine ecosystem models are formulated in terms of the aggregate properties of each model component, e.g. the mean biomass of phytoplankton per unit volume or the mean number of fish per unit area. In effect, such models follow the evolution of the "mean individual" of represented populations through time. An increasingly popular class of population models, commonly referred to as "individual-based" models, or IBMs, keep track of a number of distinct individuals within a population, each of which interacts with other individuals and its physical environment based on its present state and possibly its past history. Such models are frequently stochastic in design. Recent examples of this approach include DeAngelis et al. (1991), Rose et al. (1993), Crowder et al. (1993), Werner et al. (1993), Werner et al. (1996), and Hinckley et al. (1996). Continuing developments in computer speed and architecture have rendered the individual-based approach to fisheries modeling increasingly tractable.
Realistic population or ecosystem modeling may require an explicit treatment of spatial history. Many marine species spend their different life stages in substantially different physical environments; for example, eggs may be laid in a near-bottom, near-coastal environment, while larvae develop near the surface in shallow continental shelf waters and juvenile and adult years are spent in the deeper ocean. Even for marine species with no appreciable horizontal transport, systematic vertical migration through light, temperature, and prey concentration gradients can play a significant role in determining growth and survival.
The present work considers the simultaneous inclusion of circulation and prey fields in a spatially explicit, three-dimensional IBM for walleye pollock (Theragra chalcogramma) near Shelikof Strait, Alaska. An overview of the area and the life history of pollock spawning in Shelikof Strait is shown in Fig. 1. The early life history of this population has been studied extensively by the Fisheries Oceanography Coordinated Investigations (FOCI) program; recent summaries of this research are presented in Schumacher and Kendall (1995) and Kendall et al. (1996) . Spawned eggs develop into larvae and juveniles as they are advected to the southwest with the prevailing currents. The models we use to capture this early life history include passive advection and active vertical locomotion of individual fish through their habitat, and feeding on prey items whose concentration varies in space and time.
Specifically, we describe our experience with coupling three complex models: 1) The three-dimensional, eddy resolving, semi-spectral primitive equation circulation model (SPEM) of Haidvogel et al. (1991), adapted to this region by Hermann and Stabeno (1996). This physical model is driven by winds and runoff appropriate to the region, and has been calibrated using current meter and drogued drifter data (Stabeno and Hermann, 1996). 2) The stochastic, spatially explicit IBM of walleye pollock described by Hinckley et al. (1996). Output from an early version of this model has been compared with larval surveys spanning several years (Hermann et al., 1996). The IBM now includes prey selection based on stage and size of pollock, and the effects of turbulence on feeding, as described in Megrey and Hinckley (1998, this volume), and summarized in Fig. 2. 3) The three-dimensional Nutrient-Phytoplankton-Zooplankton (NPZ) model of Hinckley et al. (In prep). The NPZ model includes zooplankton segregated into two species groups: Neocalanus spp., the biomass dominant of the region, and Pseudocalanus spp., which are a major prey item for the larval pollock (Napp et al., 1996; Incze et al., 1997; Kendall and Nakatani, 1992). Pseudocalanus are further segregated into 13 developmental stages, spanning eggs to adult copepodites (Fig. 3). The NPZ model is formulated on a fixed three dimensional grid. Both of the biological models receive input from the circulation model in the form of currents, temperature and salinity (Fig. 4). The IBM also uses wind data directly, to calculate effective turbulence levels at larval depths through the empirical formula of MacKenzie and Leggett (1993).
In section 2, as justification for the overall modeling approach, we
present an overview of two basic categories of spatially explicit models,
Lagrangian and Eulerian, and their relative merits. In section 3, we consider
applied and theoretical issues relevant to coupling the Lagrangian biological
(IBM), Eulerian physical (SPEM), and Eulerian biological (NPZ) models,
and describe our present coupling techniques. Relevant coupling issues
include: the use of time-filtered versus unfiltered circulation fields
for tracking individuals, the choice of a time step for updating individual
positions, the use of different spatial grids for biological and physical
models, and the choice of spatial boundary conditions for each model. Issues
relevant to coupling the IBM with SPEM receive the most extensive treatment,
as we have the longest experience with these two models. In Section 4,
we describe results of float tracking experiments using SPEM output, which
bear directly on coupling issues. We then briefly describe results from
the NPZ model driven by SPEM velocities, and their effect when used as
prey fields for the IBM. Finally, we summarize computational and storage
requirements for the models as currently implemented. Section 5 presents
the conclusions.
2. Eulerian and Lagrangian Models
Spatially explicit biological models may be constructed using either Eulerian and Lagrangian frames of reference, a distinction drawn by other plankton modelers (e.g. Lande and Lewis, 1989). An Eulerian biophysical model is here defined as one which follows the evolution of some quantity at discrete, fixed physical locations. Typically these locations are the fixed grid points used by a numerical model, although analytical solutions throughout the domain are sometimes possible for simple Eulerian models. Changes in any quantity are due not only to local biological processes, but also to advective and diffusive exchange with adjacent locations, e.g.:
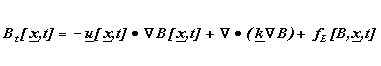 (1)
(1)
Here B represents the modeled quantity, u = (u,v,w) is the fluid
velocity, k represents horizontal and vertical eddy diffusion coefficients,
x = (x,y,z) is the spatial location, t is time, and fE
represents changes due to biological processes (birth, growth , death,
etc.) at a fixed location. This can expressed verbally as
local rate of change = advective change + diffusive change + nonconservative
biological change
Note that fE is a function of space and time, and may be either deterministic or probabilistic. This Eulerian biological model, with fE deterministic, is the form typically used by the oceanographic community for NPZ dynamics (e.g. Jamart et al., 1977; Jamart et al., 1979; Frost, 1987; Frost, 1993; Wroblewski, 1977; Lewis et al., 1994; Moisan and Hofmann, 1996a; Moisan et al., 1996; Franks and Walstad, 1997).
In the hydrodynamic literature a "Lagrangian reference frame" is one
which moves with a discrete parcel of fluid. By extension, we may define
a Lagrangian biological model as one which follows an individual
organism or group of organisms moving through space as it is advected by
the ambient currents. Mathematically we represent changes following an
individual (or group) i as:
![]() (2)
(2)
where
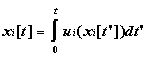 (3)
(3)
Here Bi (t) represents some property of the individual (or group) at time t, xi(t)= (xi[t],yi[t],zi[t]) represents the spatial path through time, and fL represents any nonconservative changes due to biological processes. Such changes may include processes based on past history. The quantity ui represents each component of the fluid velocity u plus any directed motions, such as vertical migration due to buoyancy or locomotion. Note the potentially "individual-based" nature of the Lagrangian model, though in fact such models need not be IBM's per se. Examples of Lagrangian models which are not individual-based include those of Flierl and Davis (1993), Botsford et al. (1994), and Moisan and Hofmann (1996b).
When a conservative (or linearly decaying) substance is being tracked (fL =fE = 0), the density of "individuals" represents concentration of the substance. In that case the Lagrangian and Eulerian approaches are in fact mathematically equivalent, and both have been used in pollutant dispersal studies. The Lagrangian approach is often found to yield better resolution of strong gradients (fronts and streaks) of concentration, due to spurious diffusion introduced by numerical techniques used to solve the Eulerian equations. Conversely, the Eulerian approach is more useful when broad spatial coverage is required (i.e. relatively uniform concentration over a wide area). Some pollutant dispersal models use the Lagrangian approach in the initial stages of dispersion from a point source, then extrapolate particle densities onto an Eulerian grid to model the later stages of dispersion (Dimou and Adams, 1992).
A Lagrangian approach (e.g. an IBM which tracks positions) is especially preferable to the Eulerian approach when past history influences present response to the environment. However, as in pollutant dispersal models, Lagrangian IBM's may require huge numbers of individuals to ensure adequate spatial coverage of the modeled population in its domain. The problem is especially acute when mortality is high and dispersion is rapid. In these situations, some way must be found of reseeding the population to make up for lost individuals; even with such reseeding there may be a steady loss of fine-scale information about the concentration field of remaining individuals. Rose et al. (1993) and Scheffer et al. (1995) have explored ways of reseeding lost individuals in spatially aggregated, high-mortality situations through random sampling of the current surviving population. Perhaps this approach could be applied to the spatially explicit IBM's as well, by treating location as another attribute of individuals. Another approach would be to extrapolate the IBM results onto an Eulerian grid once the population becomes widely dispersed. These issues merit future detailed exploration, but are beyond the scope of the present paper.
In practice, typical oceanic populations of plankton are too large,
and too widely dispersed, for an individual-based approach to be feasible
in three dimensions. One- and two-dimensional implementations have been
successful, however, for both phytoplankton (Woods and Onken, 1982; Woods
and Barkmann, 1993; Platt and Gallegos, 1980; Falkowski and Wirick, 1981)
and zooplankton (Batchelder and Williams, 1995). Here, we choose to use
an IBM for young pollock, an Eulerian NPZ model to generate prey fields,
and an Eulerian physical model (SPEM) to generate velocity, salinity and
temperature fields for both.
3. Methods for coupling Lagrangian and Eulerian models
3.a. IBM-SPEM coupling
At its core, our "Lagrangian" problem is one of accurately tracking an individual in a time- and space-variable, partially unknown environment. When a hindcast of a population for a specific time period is attempted, we must consider both the accuracy of the hindcast velocity field and the accuracy of the scheme used for tracking individuals within that velocity field. Both the physical and biological environment experienced by the tracked individuals - in particular, the prey field they experience - may be strongly affected by these factors.
The Navier-Stokes equations which form the basis of hydrodynamic models are an exact representation of the fluid evolution, but can never be solved exactly (that is, at arbitrarily high spatial and temporal resolution) on any finite computer. Nonetheless, hydrodynamic models have achieved some success in resolving both large scale and, to a lesser extent, mesoscale (~10km) velocity features of coastal and open-ocean environments. Increasingly sophisticated data assimilation schemes have allowed for ever more accurate hindcasts and forecasts of velocity fields using these equations when hydrographic and velocity data are available (e.g. Fukumori and Malanotte-Rizzoli, 1995). Even when such data are not available, or when the model is not intended as a hindcast, one may wish to reproduce the dynamics of a particular region in some statistical sense; for example, to achieve the correct scale and frequency of passage of eddies and correct mean flows, as in models of the Gulf Stream.
Ideally we wish to use a three-dimensional hydrodynamic model to generate accurate velocity fields through which individuals can be tracked in a stochastic IBM with arbitrarily high spatial and temporal resolution. Several possibilities exist for coupling a circulation model with a stochastic IBM:
i) Run the hydrodynamic and individual-based models in parallel, updating individual positions at each new time step of the hydrodynamic model. Run the combined model many times, one run for each realization of the IBM.
ii) Run the hydrodynamic and individual-based models in parallel just once, computing all realizations of the IBM simultaneously.
iii) Run the hydrodynamic model once, tracking a number of passive floats whose initial position corresponds to initial organism concentrations in the model domain. Store the resulting Lagrangian series of position, temperature, salinity, etc. for later use by an IBM without any further spatial tracking (Fig. 5a).
iv) Run the hydrodynamic model once, storing all relevant gridded velocity, temperature, and salinity fields at each model gridpoint and time step, for subsequent use by an IBM which performs its own spatial tracking (Fig. 5b).
All approaches have both advantages and drawbacks. Method i) is at present computationally prohibitive for most three-dimensional hydrodynamic models, as it requires a potentially large number of runs. Method ii) reduces computation of the physical model, but requires huge amounts of computer memory to keep track of all the biological realizations simultaneously. Method iii) is efficient and allows for many individuals, but eliminates the possibility of adding individual behaviors (in particular, vertical locomotion) which vary as a function of the individual's unique, partly random, life history. In other words, any realization of the IBM in method iii) cannot feed back on the float tracks, which are determined by the hydrodynamic model alone. Method iv) offers the possibility of feedback, but requires potentially huge amounts of data storage to accommodate the three-dimensional circulation model output. Hence we propose a modification of iv):
iv-a) Run the hydrodynamic model once, storing suitably low-pass filtered (high frequencies removed), decimated time series of all relevant gridded velocity, temperature, and salinity fields at each model gridpoint, for subsequent use by an IBM which performs its own spatial tracking.
Note that the characteristics of the filter used in iv-a), and the interval for subsampling, depend on what portion of the full spectrum of motions is considered "expendable" for purposes of spatial tracking. For example, time-filtering would introduce a bias if locomotion of individuals were somehow correlated with higher frequency current fluctuations (e.g. swimming in response to tides or internal waves), that had been removed. In general, primitive equation hydrodynamic model output contains far less energy at superinertial frequencies than is observed in real oceanographic measurements, and such fluctuations that do exist in the model are poorly correlated with the real data. Nevertheless, subsampling without filtering, while partially adequate for spatial tracking, could lead to serious aliasing errors when much high frequency energy is present. We suggest filtering be done to eliminate this poorly correlated high frequency band, but retain significantly correlated subinertial motions. The significance of tides is context-dependent, and needs to be considered carefully.
Consider how spatial tracking in method iv-a) might be efficiently accomplished
with the filtered fields, and whether any of the information lost in the
filtering process might be added back in by the tracking algorithm. Neutrally
buoyant floats have been tracked in many numerical ocean models. Instantaneous
float velocities are generally derived by interpolating between gridpoints
to the current location of each float. Generally the floats are advanced
in time using the same time step as is used for solving the governing hydrodynamic
equations, but this need not be the case, and especially not in our situation
where previously stored, filtered velocity fields are used. How, then,
to choose a time step for float tracking which is sufficiently short but
not computationally prohibitive? One requirement for successful float tracking
is that the Lagrangian decorrelation time TL be much longer
than the time step dt used for float tracking:
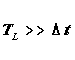 (4)
(4)
The property TL is defined as follows. When moving within
a turbulent flow field, particle velocities eventually become decorrelated
from their starting velocities. This loss of "memory" can be characterized
by the integral of the lagged correlation function:
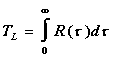 (5)
(5)
where
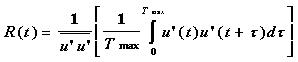 (6)
(6)
here u'u' is the mean turbulent kinetic energy of the flow, u'i(t) is the velocity of the particle i at time t, Tmax is a suitably long time used for averaging and {} denotes an ensemble mean over all particles.
When eq. (4) is satisfied, the moving float (individual) can be reasonably approximated to travel at constant velocity for a period of time which is longer than the time between updates of the velocity field used for tracking. When this not the case, float tracks will diverge from "true" particle paths. (Haidvogel [1982] has also demonstrated that adequate spatial resolution is crucial for accurate float tracking; with overly coarse resolution, nonlinear interactions present in the hydrodynamic equations will be improperly represented and floats will diverge from their true path as a result).
We generally expect time-filtering of velocities to increase TL. This is helpful in allowing a longer time step for tracking, as well as reducing the size of the velocity file, if the higher-frequency variability can be reasonably sacrificed. If tides are a critical aspect of the individual's life history, there may be no easy way to avoid using unfiltered velocities, and a short tracking time step. Note, however, that some information about tides could be stored in compact form (amplitude and phase) for later use; such reconstructed tidal velocities could be added to filtered (subtidal) velocity fields directly in the tracking algorithm, potentially reducing storage requirements.
The model used in the present study is a prognostic, rigid-lid, hydrostatic,
three-dimensional, primitive equation model of velocity and salinity fields
in the northern Gulf of Alaska. Details of model construction and sensitivity
analyses may be found in Hermann and Stabeno (1996). Stabeno and Hermann
(1996) demonstrated that the model yields realistic mean flows and eddy
statistics (frequency of passage of mesoscale eddies) in the vicinity of
Shelikof Strait. There are no explicit tides in this model, but some high-frequency
(near-inertial) oscillations are included in the dynamics. Boundary conditions
were provided using a telescoped grid with a toroidal, re-entrant channel,
as discussed in Hermann and Stabeno (1996). The finely resolved portion
of the model domain (4 km mean spacing) is shown in Fig. 1; the finely
resolved area extends from the entrance of Shelikof Strait to slightly
westward of the Shumagin Islands, and southward to just beyond the Alaskan
Stream.
3.b. NPZ-SPEM coupling
The characteristic length and time scales of biological properties are strongly influenced by the corresponding scales of their physical environment, but are not identical to them. Ideally we would like to resolve both fields so finely in space and time that all relevant scales are included, but this is rarely possible due the cost involved. As a compromise, we chose different horizontal and vertical scales for the Eulerian physical and biological models. For NPZ dynamics, we generally require a finer vertical scale than for the physical model due to the sensitivity of primary production to changes in mixed layer depth. This entails a sacrifice of horizontal resolution. The character of mesoscale eddies in the vicinity of Shelikof Strait suggests a horizontal spacing of ~12 km as a desirable goal; note, however, that the useful resolution for our NPZ model is fundamentally dependent on the characteristic scales of the modeled circulation, rather than the characteristic (and typically finer) scales of the circulation itself. As a first attempt, we chose to use a model with 1 meter resolution in the vertical, and 20 km resolution (5x the physical model) in the horizontal (Fig. 6). Vertical coverage is from 0 to 100 m depth. Background horizontal and vertical diffusivities in the NPZ model were set at 10 and 10-5 m2 s-1, respectively.
As with the IBM, we use time-filtered, stored output from the physical model as input for the NPZ model. Time-filtered barotropic streamfunction output from the physical model is subsampled to the grid of the NPZ model. The horizontal gradients of the barotropic streamfunction, divided by the water column depth (or by 100 m in regions of deeper bathymetry), yields depth averaged velocities at each horizontal location. These are used to calculate the horizontal divergence and, subsequently, the vertical velocities. This approximation distorts the true vertical shear and vertical velocities, but avoids spurious (and potentially very large) convergence which typically results from subsampling a full three-dimensional velocity field. Errors in the computed vertical velocity field are likely not too significant for the present case; vertical upwelling of nutrients strongly affects production in some parts of the ocean, but in the Gulf of Alaska downwelling predominates during most of the year. Horizontal advection and mixed layer deepening are hence the more significant sources of nutrients to feed production in this area.
The vertical structure of the NPZ model assumes a mixed layer of variable depth with uniform properties, and a stratified region beneath (down to 100m), where mixing is based on the spatially constant background diffusivity. Mixed layer depth (MLD) time series were generated for the NPZ model using the circulation model's density profiles at the horizontal locations of the NPZ grid. A simple algorithm is presently employed, where MLD is defined as that depth where the salinity field (the primary determinant of density in this region during spring) assumes a value 0.05 psu greater than the surface value. Clearly this is a crude parameterization, hence future circulation modeling in this region will include explicit mixed layer physics.
Since we have used stored, time-filtered and decimated streamfunction fields to drive the NPZ model, we must consider the effects of that filtering on the prey dynamics. Float tracking experiments suggest an acceptable loss of temporal information for our rigid lid circulation model with no tides (see Results section). The effect of varying spatial resolution on the NPZ fields depends on the magnitude of the advection terms, relative to the local nonconservative (biological) dynamics. If biological dynamics predominate over advective change, then coarse resolution of the advective terms is a permissible compromise. We may ultimately be able to invoke spatially dependent diffusivities, to partially compensate for the loss of spatial resolution. In Shelikof Strait biological components with the fastest turnover times (phytoplankton in our NPZ model) will be the least succeptible to aliasing from the choice of a coarse spatial grid, while those with longer turnover times will be most affected. Napp et al. (1996) have demonstrated that advection plays a large role in determining the spatial patterns of phytoplankton and zooplankton ovserved in Shelikof Strait. Future iterations of our coupled SPEM-NPZ models will examine the consequences of decreasing the spatial scale.
The NPZ model domain is a subset of the physical model, and needs boundary conditions for each of its biological variables. In the interior, the balance of eq (1) holds; separating out the spatial terms yields:
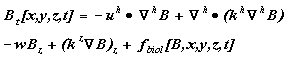 (7)
(7)
where B is an NPZ model variable (e.g. Phytoplankton), Lh is the horizontal gradient operator, uh ,vh ,kh are the horizontal velocities and eddy diffusivity, w is the vertical velocity, kz is the vertical eddy diffusivity and fbiol represents all nonconservative biological dynamics. Perfect knowledge of upstream values would permit direct specification of B at the upstream boundary; instead, we are limited to several springtime measurements per year taken 7 km apart along a transect accross the lower exit region of Shelikof Strait (Napp et al., 1996; Incze et al., 1997; Incze and Ainaire, 1995). Hence, we provide values at the upstream end by running the model in one-dimensional mode (no advection or horizontal diffusion), with assimilation of observed values at those locations.
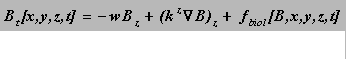 (8)
(8)
where nudge is the nudging constant and Bdata is the available data. Nudging is currently implemented for Pseudocalanus nauplii in the mixed layer; we use nudge = 0.5 d-1 during periods when data were available (mid-April through mid-May). Boundary values computed using eq. (8) are advected into the interior, driven by the velocity field and the horizontal gradient term of eq. (7). The assimilation, through nudging, of the boundary data is a way of compensating for our ignorance about the true boundary values; eq (8) may be thought of as a dynamically consistent interpolator of boundary values. It is similar in spirit to a class of physical boundary conditions which combine simplified physics (e.g. wave dynamics) with nudging towards observed values.
At the downstream boundary, a zero gradient condition was imposed for
all biological variables.
![]() (9)
(9)
3.c. IBM-NPZ coupling
Some of the issues discussed above for the proper application of stored circulation fields to the IBM hold for the application of Eulerian biological fields to the IBM as well. Ideally we could interpolate perfectly accurate Eulerian prey values onto the location and time of the tracked individuals of the Lagrangian IBM. In practice we must settle for statistically correct prey fields, driven in part by the statistically correct velocity fields from the physical model. The mapping of prey values to individual fish locations is straightforward, and is performed in the IBM using simple linear interpolation of NPZ model output in time and space.
Boundary conditions for the IBM are presently as follows. 1) When an
individual is located outside the NPZ model domain, we apply the prey values
of the NPZ boundary point nearest that individual's present location. 2)
When an individual is advected outside the finely resolved circulation
model domain, it is removed from the population. We also trap individuals
at the downstream (southwestern) end of the physical domain, to prevent
their re-entrance at the upstream end.
4. Results
4.a. Float tracking experiments
To help address the accuracy of float tracking with pre-stored, filtered and decimated velocity fields, versus "direct" tracking with the unfiltered field, we present results from a simulation of 1987 currents and float tracks in the Gulf of Alaska. Details of model forcing for this year are available in Hermann et al. (1996). In Fig. 7a we illustrate the results of float tracking by direct updating (case a) in the hydrodynamic model; that is, ten floats are tracked using the instantaneous velocity produced by the model at each time step with a 4th-order Runge-Kutta scheme. The time step for this model is .0375 hr. Interpolation of velocities between model gridpoints is performed as described in Hoffmann et al. (1989); briefly, this entails linear interpolation in the horizontal and spectral (here, Chebyshev) expansion in the vertical. Initial positions span a northwest-southeast line between the Alaska Peninsula and the northwestern corner of Kodiak Island, at 40 m depth. Many of the floats circulate around and through a cyclonic-anticyclonic eddy pair, just downstream from the exit of Shelikof Strait. Note how some of the floats, released in deep regions, cross bathymetric contours to the shallower continental shelf.
In Figs. 7b-7d we illustrate the same set of floats, this time tracked with pre-stored, filtered and decimated velocity fields. These fields are produced by applying a cosine-Lanczos 30-hour low-pass filter to the original model time series during execution of the run, and storing the filtered result once per day. This filtering process eliminates all of the near-inertial, internal wave oscillations. We wish to see if accurate float tracking can be achieved with time steps longer than the .0375 hr of the "direct" unfiltered method, and whether the resulting tracks compare favorably with those derived using the unfiltered method. Float tracking is attempted with three different values of the time step: b) dt =1 hour; c) dt = 0.2 hour; d) dt = .04 hour. Linear interpolation in time is used to provide velocity values in between the stored daily values; spatial interpolation is performed as in case a. In each case floats are seeded at the same locations and depths as in case a. In case b (Fig. 7b), the broadly defined paths of the float tracks from case a (Fig. 7a) are reasonably well reproduced, but the details of the paths differ as the floats are advected downstream. Can a shorter time step do better? Case c (Fig. 7c) differs from case b primarily in the improved fit with features in the vicinity of the Shumagin Islands (55° N, -160° E). Case d (Fig. 7d), with highest temporal resolution, exhibits no substantial difference from case c.
In Fig. 8 we plot the root-mean-squared (rms) horizontal displacement of the floats in case b from their corresponding locations in case a, the displacement of floats between cases b and c, and the displacement between cases c and d. During the first four days of simulation, case b generates float tracks within ~2 km of their locations in case a. Thereafter case b results diverge from case a, to a mean displacement of ~40 km (the typical width of the deep strait and sea valley in this area). Near day 30, the mean displacement increases once more, ultimately achieving values of ~140 km. Cases b and c diverge significantly from each other after day 30 while cases c and d are essentially identical through day 60.
Apparently, by shortening the time unit from 1 hour to 0.2 hour, we sufficiently converge on the "true" solution for the filtered velocity field, that is, we have achieved a time step sufficiently shorter than the Lagrangian decorrelation time for the filtered velocities to yield an accurate result. This justifies the use of a time step of 0.2 hour in the float tracking algorithm described in Hinckley et al (1996); the same time step and spatial interpolation method is used to generate the results shown in Section 4.b.
Fewer of the float tracks cross into shallow shelf areas when filtered velocities are used, compared to the unfiltered technique. In future studies, this deficiency could be addressed to some extent by adding a suitable random walk component to the tracked floats, an equivalence first noted by Taylor (1921). We caution, however, that the diffusivity lost by temporal filtering may be spatially dependent, and that spatial variation in the magnitude of a random walk can pose special difficulties (Hunter et al., 1993; Holloway, 1994).
The importance of vertical position in determining the paths of individuals
was noted by Hinckley et al. (1996). In Fig. 9, we underscore this point
by plotting float paths as in case c, but with all floats constrained to
remain at 40 m depth, rather than being free to follow the flow field in
three dimensions. The influence of the eddy field is markedly reduced by
this constraint; floats do not circulate around the eddy pair as they did
in other cases.
4.b. Coupled run output, timing and storage
Some illustrative results from the coupled models for mid-June, 1987 are shown in Figs. 10a-c. A total of 1600 individuals are used in the IBM, with mortalities set to zero. A cyclonic eddy is located in the deepest part of the sea valley, near 56.5 ° N, -156 ° E (Fig. 10a). Total numbers of all copepodite stages of Pseudocalanus are shown for zooplankton (Fig. 10b). Positions of individual fish are shaded according to length (Fig. 10c). The individual lengths vary, due to the different prey fields encountered during their life history; larvae greater than 8 mm ingest a mixture of nauplii and copepodites. A cluster of medium-sized larvae (8-16 mm) is trapped within the eddy. A tongue of low zooplankton concentration is being advected around the southern rim of the eddy, and shorter fish are associated with that feature. A tongue of higher zooplankton concentration, advecting around the northern rim of the eddy, has fewer but generally longer fish associated with it. Regions downstream and shoreward of this feature also exhibit greater lengths.
While some patchiness of fish size can be produced through purely kinematic effects related to the time of spawning (e.g. a cluster of late-spawned, smaller individuals trapped in an eddy), clearly the spatially variable prey field contributes to the patchiness of fish attributes in this model. The use of a dynamic prey field also results in different mean growth and survival for groups of individuals spawned at different places and times (Hinckley et al., 1988, this volume).
All model results described here were generated using a CRAY Y-MP vector
processing supercomputer. Statistics of runs and output files are listed
in Table 1. As shown, the physical model consumes the largest amount of
computer time. Indeed, this is the primary motivation for decoupling the
physical and biological runs; by decoupling we allow for much more testing
and sensitivity analysis of the biological models. The output files from
the physical model, while large, are not prohibitively so, and can be transferred
to local workstations for detailed analysis and plotting. Statistics of
the IBM are dependent on the number of individuals followed.
5. Conclusions and future work
Spatially explicit biophysical models, spanning multiple trophic levels, can be a powerful tool for probing hypotheses about the early life history of marine fish. Throughout our ongoing work with coupled hydrodynamic, population (IBM), and trophodynamic (NPZ) models, we have attempted to balance desirable features with practical limits on computing power. Our experience thus far has led to the following conclusions. 1) Storage of pre-filtered and decimated model velocity and scalar fields, for later use by Lagrangian biological models, is both feasible and efficient using presently available computers. Supercomputing platforms with reasonable large (several gbyte) storage capacity are necessary for much of this work, however. 2) The results are reasonably accurate given a sufficiently small time step for spatial tracking; however, care must be taken to consider the information lost through filtering. Practical techniques exist to recover some of the lost information, such as tides. 3) Spatially varying prey fields, derived using a traditional Eulerian approach, can be applied in a straightforward manner to spatially explicit (Lagrangian) IBM's, and should typically enhance the variance of individual attributes. 4) Boundary conditions for Eulerian prey models should benefit from a careful use of data assimilation, when field data are available.
As our models evolve to greater complexity, there is a continuing need
for calibration and sensitivity analyses of the coupling methods which
link them. For example, there is a strong need for further sensitivity
analyses of grid spacing in the NPZ model. Equally important is the need
for further comparison of three-dimensional NPZ model output with chlorophyll
and zooplankton data. For chlorophyll, satellite-derived estimates may
be useful for comparing at least broad spatial patterns, and possibly higher-order
spatial statistics, with those produced from the model. These and other
issues will be explored in future reports.
Acknowledgements
This is contribution number 1920 from NOAA/ Pacific Marine Environmental
Laboratory, contribution number 318 to NOAA's Fisheries Oceanography Coordinated
Investigations, and contribution number 475 from the Joint Institute for
the Study of the Atmosphere and Oceans under cooperative agreement NA90RAH00073.
Batchelder, H. P. and Williams, R. (1995). Individual-based modeling
of the population dynamics of Metridia lucens in the North Atlantic.
ICES J. Mar. Sci. 52: 469-482.
Botsford, L. W., Moloney, C. L., Hastings, A., Largier, J. L., Powell,
T. M., Higgins, K., and Quinn, J. F. (1994). The influence of spatially
and temporally varying oceanographic conditions on meroplanktonic metapopulations.
Deep-Sea Res. 41 107-145.
Crowder, L. W., Rice, J. A., Miller, T. J., and Marschall, E. A. (1993).
Empirical and theoretical approaches to size-based interactions and recruitment
variability in fishes. In DeAngelis, D. L., Gross, L. J. (eds.) Individual-Based
Models and Approaches in Ecology, Chapman and Hall, pp. 237-255.
DeAngelis, D. L., Godbout, L., and Shuter, B. J. (1991). An individual-based
approach to predicting density-dependent dynamics in smallmouth bass populations.
Ecol. Model. 57 91-115.
Dimou, K. N. and Adams. P E. (1991). Representation of sources in a
3-D Eulerian-Lagrangian mass transport model. In Wrobel, L. C., Brebbia,
C. A. (eds.) Water Pollution Modeling, Measurement and Prediction 1991,
pp. 251-264.
Falkowski, P. G., and Wirick, C. D. (1981). A simulation model of the
effects of vertical mixing on primary productivity. Mar. Biol. 65 69-75.
Flierl, G. R., and Davis, C. S. (1993). Biological effects of Gulf Stream
meandering. J. Mar. Res. 51 529-560.
Franks, P. J. S. and Walstad, L. J. (1997). Phytoplankton patches at
fronts: a model of formation and response to wind events. J. Mar. Res.
55: 1-29.
Frost, B. W. (1987). Grazing control of phytoplankton stock in the open
subarctic Pacific Ocean a model assessing the role of mesozooplankton,
particularly the large calanoid copepods Neocalanus spp. Mar. Ecol.
Prog. Ser. 39 49-68.
Frost, B. W. (1993). A modelling study of processes regulating plankton
standing stock and production in the open subarctic Pacific Ocean. Prog.
Oceanogr. 32 17-56.
Fukumori, I. and Malanotte-Rizzoli, P. (1995). An approximate Kalman
filter of ocean data assimilation: an example with an idealized Gulf Stream
model. J. Geophys. Res. 100(C4): 6777-6793.
Haidvogel, D. B., Wilkin, J. L. and Young, R. (1991). A semi-spectral
primitive equation ocean circulation model using vertical sigma and orthogonal
curvilinear coordinates. J. Comput. Phys. 94: 151-185.
Haidvogel, D. (1982). On the feasibility of particle tracking in Eulerian
ocean models. Ocean Modelling 45 4-9.
Hermann, A. J. and Stabeno, P. J. (1996). An eddy resolving model of
circulation on the western Gulf of Alaska shelf. I. Model development and
sensitivity analyses. J. Geophys. Res.101(C1): 1129-1149.
Hinckley, S., Hermann, A. J., and Megrey, B. A. (1996). Development
of a spatially explicit, individual-based model of marine fish early life
history. Mar. Ecol. Prog. Ser.139: 47-68.
Hinckley, S., Hermann, A. J., Meir, K. L. and Megrey, B. A. (1998).
The importance of spawning location and timing to successful transport
to nursery areas: a simulation modeling study of Gulf of Alaska walleye
pollock. This volume.
Hoffmann, E. E., Hedstrom, K. S., Moisan, J. R., Haidvogel, D. B., and
Mackas, D. L. (1991). The use of simulated drifter tracks to investigate
general transport patterns and residence times in the coastal transition
zone. J. Geophys. Res. 96 15,041-15,052.
Holloway, G. (1994). On modeling vertical trajectories of phytoplankton
in a mixed layer. Deep-Sea Res. II 41 957-959.
Hunter, J. R., Craig, P. D., and Phillips, H. E. (1993). On the use
of random walk models with spatially variable diffusivity. J. Comput. Phys.
106 366-376.
Incze, L. S., Siefert, D. W., and Napp, J. M. (1996). Mesozooplankton
of Shelikof Strait, Alaska: abundance and community composition. Cont.
Shelf Res. 17: 287-305.
Jamart, B. M., Winter, D. F., Banze, K., Anderson, G. C., and Lam, R.
K. (1977). A theoretical study of phytoplankton growth and nutrient distribution
in the Pacific Ocean off the northwestern U.S. coast. Deep-Sea Res. 24
753-773.
Jamart, B. M., Winter, D. F., and Banze, K. (1979). Sensitivity analysis
of a mathematical model of phytoplankton growth and nutrient distribution
in the Pacific Ocean off the northwestern U. S. coast. J. Plank. Res. 1
267-290.
Kendall, A. W., Jr. and Nakatani, T. (1992). Comparisons of early life
history characteristics of walleye pollock Thergra chalcogramma
in Shelikof Strait, Alaska and Funka Bay, Hokkaido, Japan. Fish. Bull.
90: 129-138.
Kendall, A. W., Jr., Schumacher, J. D. and Kim, S. (1996). Walleye pollock
recruitment in Shelikof Strait: applied fisheries oceanography. Fish. Oceanogr.
5 (suppl.): 4-18.
Lande, R. and Lewis, M. R. (1989). Models of photoadaptation and photosynthesis
by algal cells in a turbulent mixed layer. Deep Sea Res. 36: 1161-1175.
Lewis, C. V. W., Davis, C. S., and Gawarkiewicz, G. (1994). Wind forced
biological-physical interactions on an isolated offshore bank. Deep-Sea
Res. 41 51-73.
MacKenzie, B. R. and Leggett, W. C. (1993) .Wind-based models for estimating
the dissipation rates of turbulent energy in aquatic environments: Empirical
comparisons. Mar. Ecol. Prog. Ser. 94: 207-216.
Megrey, B. A. and Hinckley, S. (1998). The effect of turbulence on feeding
of larval fishes: a sensitivity analysis using an individual based model.
This volume.
Moisan, J. R. and Hofmann, E. E. (1996a). Modeling nutrient and plankton
processes in the Coastal Transition Zone. Part 1: A time- and depth-dependent
model. J. Geophys. Res. 101(C10): 22647-22676.
Moisan, J. R. and Hofmann, E. E. (1996b). Modeling nutrient and plankton
processes in the Coastal Transition Zone. Part 3: Lagrangian drifters.
J. Geophys. Res. 101(C10): 22693-22704.
Moisan, J. R., Hofmann, E. E. and Haidvogel, D. B. (1996). Modeling
nutrient and plankton processes in the Coastal Transition Zone. Part 2:
A three-dimensional physical-bio-optical model. J. Geophys. Res. 101(C10):
22677-22691.
Napp, J. M., Incze, L. S., Ortner, P. B., Siefiert, D. L. W., and Britt,
L. (1996). The plankton of Shelikof Strait, Alaska: standing stock, production,
mesoscale variability and their relevance to larval fish survival. Fish.
Oceanogr. 5 (suppl. 1): 19-38.
Platt, T., and Gallegos, C. L. (1980). Modeling primary production.
In Falkowski, P. G. (ed.) Primary Productivity in the Sea, , Plenum Press,
New York, 531 pp.
Rose, K. A., Christensen, S. W., and DeAngelis, D. L. (1993). Individual-based
modeling of populations with high mortality: a new method for following
a fixed number of model individuals. Ecol. Model. 68 273-292.
Scheffer, M., Baveco, J. M., DeAngelis, D. L., Rose, K. A., and Van
Nes, E. H. (1995). Super-individuals: a simple solution for modelling large
populations on an individual basis. Ecol . Model. 80: 161-170.
Schumacher, J., and Kendall, A. W. Jr. (1995). An example of fisheries
oceanography: Walleye pollock in Alaskan waters. U. S. Nat. Rep., Int.
Union Geod. Geophys. 1991-1994, Rev. Geophys. 33: 1153-1163.
Stabeno, P. J., and Hermann, A. J. (1996). An eddy resolving model of
circulation on the western Gulf of Alaska shelf. 2. Comparison of results
to oceanographic data. J. Geophys. Res.101(C1): 1151-1161.
Taylor, G. I. (1921). Diffusion by continuous movements. Proc. London
Math. Soc. (ser. 2) 10: 196-212.
Werner, F. E., Page, F. H., Lynch, D. R., Loder, J. W., Lough, R. G.,
Perry, R. I., Greenberg, D. A. and Sinclair, M. M. (1993). Influences of
mean advection and simple behavior on the distribution of cod and haddock
early life stages on Georges Bank. Fish. Oceanogr. 2: 43-64.
Werner, F. E., Perry, R. I., Lough, R. G. and Naimie, C. E.. (1996).
Trophodynamic and advective influences on Georges Bank larval cod and haddock.
Deep-Sea Res. 2 (Top. Stud. Oceanogr.) 43: 1793-1822.
Woods, J., and Barkmann, W. (1993). Diatom demography in winter - simulated
by the Lagrangian Ensemble method. Fish. Oceanogr. 2 202-222.
Woods, J. D., and Onken, R. (1982). Diurnal variation and primary production
in the ocean - preliminary results of a Lagrangian ensemble method. J.
Plankton Res. 4 735-756.
Wroblewski, J. S. (1977). A model of phytoplankton plume formation during variable Oregon upwelling. J. Mar. Res. 35 357-394.
Figure
1. Summary of early life history for walleye pollock spawning at the exit
of Shelikof Strait. Primary regional currents are shown in inset. Subsequent
to spawning, hatched larvae from eggs drift southwest with the Alaska Coastal
Current; some are transported up onto the shallow, near-coastal shelf area
while others are transported out into the deeper waters of the Alaskan
Stream. Dashed line indicates the boundary of the finely resolved physical
model domain (~4 km mean spacing).
Figure
2. Summary of the individual-based model structure.
Figure
3. Summary of the NPZ model structure.
Figure
4. Summary of coupling among the physical and biological models.
Figure
5. Two schemes for implementing a Probabilistic-Lagrangian biophysical
model of the early life stages of marine fish. Schematic a) represents
scheme iii) described in the text; b) represents scheme iv) described in
the text. "SPEM" refers to the Semispectral Primitive Equation Model of
Haidvogel et al. (1991), used for generating ocean current, salinity and
temperature fields. "IBM" refers to the Individual-Based Model of marine
fish. [.]i(t) refers to the value of some physical or biological
quantity associated with individual i.
Fig. 6.
Overlay of SPEM (+) and NPZ (o) model grids. Horizontal grid spacing
of the NPZ grid is 5x larger than the SPEM grid. Triangles () indicate
upstream locations where Pseuodocalanus values are nudged to available
data.
Figure 7. a)
Float tracks generating by directly updating float positions at each time
step in a hydrodynamic model (SPEM) simulation of 1987. Ten floats, released
along a cross-shelf line at 40m depth on DOY 135 for 1989, are shown. Tracks
are coded by time interval: DOY 135-165 (black); DOY 165-195 (red); DOY
195-225 (green); DOY 225-255 (dark blue); DOY 255-270 (light blue). Model
bathymetry (meters) is shown in greyscale.b)
Float tracks generated by updating float positions using previously stored,
filtered, daily velocity fields, with dt=1.0 hour for the float tracking
algorithm. c)
Results as in (b) using dt=0.2 hour for the float tracking algorithm. d)
Results as in (b) using dt=0.04 hour for the float tracking algorithm.
Figure
8. Root-mean-square relative displacement of floats tracks among the various
tracking experiments. Black line - filtered velocities with dt=1.0
hour (case b) versus "direct" tracking (case a). Red line - filtered velocities
with dt=1.0 hour (case b) versus dt=0.2 hour (case c). Green line - filtered
velocities with dt=0.2 hour (case c) versus dt=0.04 hour (case d). Mean
relative displacement in each case is plotted as a function of time since
the beginning of the experiment (DOY 105, 1987).
Fig. 9.
Float tracks generating by directly updating float positions at each time
step in a hydrodynamic model (SPEM) simulation of 1987, where all floats
are constrained to remain at 40m depth. Initial float positions and
coding of tracks are as in Fig. 6.
Fig. 10. Results of coupled models for mid-June, 1987. a)
Surface velocities (m s-1) from the circulation model. b)
NPZ model output. Shading represents total concentration of all copepodite
stages of Pseudocalanus spp. in the mixed layer (# m-3). Bathymetry
is shown by solid lines (m) and barotropic streamfunction is shown by dashed
lines (contour interval is 0.1 x 10^6 m^3/s coastward of the shelf break
and 1.0 x 10^6 seaward. c)
IBM output. Positions of individual pollock are shaded by length (mm).
Table 1. Timing and Storage statistics for the three coupled models.
| Model type | Circulation
(SPEM) |
Prey
(NPZ) |
Pollock
(IBM) |
| Model size | 257x97x9 gridpoints | 20x20x100
gridpoints |
1600
individuals |
| Resolution | 4 km horiz
5 m vert |
20 km horiz
1 m vert |
4 km horiz
5 m vert |
| Daily output | velocity
salinity temperature |
Nitrate concentration
Phytoplankton biomass Zooplankton biomass (14 stages/species) |
length
weight position |
| Length of simulation (days) | 270 | 95 | 210 |
| Output file size (gbytes) | 1.0 | 0.5 | .02 |
| CRAY YMP CPU (hours) | 125 | 5 | 5 |