U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
On the Variability of Winds, Sea Surface Temperature, and Surface Layer Heat Content
in the Western Equatorial Pacific
Michael J. McPhaden and Stanley P. Hayes
NOAA/Pacific Marine Environmental Laboratory, Seattle, Washington
Journal of Geophysical Research, 96, supplement, 3331-3342 (1991)
This paper is not subject to U.S. copyright. Published in 1991 by the American Geophysical
Union.
In this study we examine the surface layer heat balance using wind, current, and
temperature data from equatorial moorings along 165°E. The analysis focuses primarily on
daily to monthly time scale variations during the 1986-1987 El Niño/Southern Oscillation
event. The period is one of high mean sea surface temperatures ( 29°C) and frequent outbreaks of westerly winds. We infer
that evaporative cooling related to wind speed variations accounts for a significant
fraction of the observed sea surface temperature (SST) and upper ocean heat content
variability. This evaporative heat flux converges nonlinearly in the surface layer, giving
rise to larger temperature variations in the upper 10 m than below. Other processes
examined (wind-forced vertical advection and entrainment, lateral advection) were
negligible or of secondary importance relative to evaporative cooling. A large fraction of
the SST and surface layer heat content variance could not be directly related to wind
fluctuations; this unexplained variance is probably related to shortwave radiative fluxes
at the air-sea interface.
29°C) and frequent outbreaks of westerly winds. We infer
that evaporative cooling related to wind speed variations accounts for a significant
fraction of the observed sea surface temperature (SST) and upper ocean heat content
variability. This evaporative heat flux converges nonlinearly in the surface layer, giving
rise to larger temperature variations in the upper 10 m than below. Other processes
examined (wind-forced vertical advection and entrainment, lateral advection) were
negligible or of secondary importance relative to evaporative cooling. A large fraction of
the SST and surface layer heat content variance could not be directly related to wind
fluctuations; this unexplained variance is probably related to shortwave radiative fluxes
at the air-sea interface.
1. Introduction
The western equatorial Pacific is characterized by mean sea surface temperatures
that are among the warmest in the world ocean. This region is also characterized
by vigorous air-sea interaction, because turbulent heat exchange between the
ocean and the atmosphere is a highly nonlinear function of sea surface temperature
(SST). In extreme cases, air-sea interactions in the western Pacific may lead
to El Niño/Southern Oscillation (ENSO) events, which are coupled ocean-atmosphere
phenomena occurring every 4-7 years [Rasmusson
and Wallace, 1983]. ENSO has global climatic impacts, some of which
can be traced to western Pacific SST anomalies of  1°C
[e.g.,
Nicholls, 1985; Palmer
and Mansfield, 1984]. These impacts may be predictable months to years
in advance, provided that the processes involved in SST change can be understood
and reliably modeled.
1°C
[e.g.,
Nicholls, 1985; Palmer
and Mansfield, 1984]. These impacts may be predictable months to years
in advance, provided that the processes involved in SST change can be understood
and reliably modeled.
While it is generally conceded that understanding SST variability is important
for understanding and predicting ENSO, little is known quantitatively about
the atmospheric and oceanic processes that control this variability. The purpose
of this study therefore is to examine the relationship between wind forcing,
SST, and surface layer heat content, using data from a near-equatorial moored
array along 165°E. The analysis is a continuation of that presented by McPhaden
[1989] and focuses mainly on time scales of days to months. The period
of study coincides with the 1986-1987 ENSO, during which pronounced interannual
variations occurred throughout the tropical Pacific (Figure
1) (see also Kousky
and Leetmaa [1989]; McPhaden
et al., [1990]).
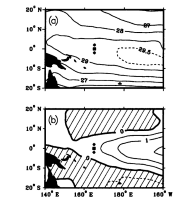
Fig. 1. (a) Average SST and (b) SST anomaly in the western
tropical Pacific for December 1986 to October 1987, based on data from the National
Meteorological Center [Reynolds,
1988]. Contour interval is 1°C in Figure 1a, except that the 29.5°C
isotherm is shown as dashed curve. Contour interval in Figure 1b is 0.5°C,
with positive values shown as solid contours and negative values shown as dashed
contours. Hatching in Figure 1b indicates regions of negative SST anomaly.
The current meter mooring (solid square) and ATLAS moorings (solid diamonds)
are also indicated.
The paper is outlined as follows. Section 2 briefly describes the data used in this
study. This is followed in section 3 by discussion of the mechanisms that are potentially
important in controlling SST and surface layer heat content. In section 4 we describe the
spatial structure of temperature and wind variations observed from the moored array. Then
in section 5 we discuss how these variations may be related to turbulent heat fluxes
across the air-sea interface, vertical advection, and entrainment from the thermocline.
Lateral advection in the surface layer is discussed in section 6. Major results and
conclusions are summarized in section 7.
2. Data
The data used in this study were collected from three surface moorings located
at 2°N, 0°, and 2°S, 165°E in the western Pacific warm pool (Figure
1). Winds were measured on all three moorings at a height 4 m above mean
sea level from wind recorders mounted on the surface toroid (Figure
2). Temperatures were measured at 15 depths on the equatorial mooring and
11 depths on ATLAS thermistor chain moorings at 2°N and 2°S (Figure
3). In each case the shallowest measurement was at 1 m (nominally termed
SST) and the deepest was at 500 m. Currents were measured on the equatorial
mooring using EG&G Model 610 Vector Averaging Current Meters (VACMS) at
six depths, although for this study, only the 50-m record will be considered
(Figure 14). All variables were processed to daily averages; however, hourly
averaged wind data were first used to estimate wind speed, wind stress, and
wind work in (2), (3), and (5) (given below) before computing daily means. Record
lengths for winds, temperatures, and currents are explicit in Figures 2, 3 and
14, respectively. Longer records are available from these moorings (see McPhaden
et al. [1990]), although the period from December 13, 1986, to October
14, 1987, has the most complete vertical temperature coverage at the equatorial
site coincident with reliable wind information during 1986-1987. Further details
concerning instrumental accuracies, sampling characteristics, and data processing
are given by Freitag
et al. [1987] and McPhaden
et al. [1990].
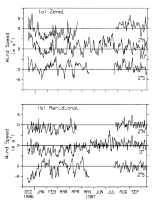
Fig. 2. (a) Zonal and (b) meridional winds for December 13, 1986, to
October 14, 1987, at 2°N, 0° and 2°S along 165°E.

Fig. 3. Contours of daily averaged temperatures at 2°S, 0°, and 2°N along 165°E
for December 13, 1986, to October 14, 1987. Contour interval is 2°C, except that the
29°C contour is shown as a dashed curve. Sensor depths are indicated on the left axis; 7
days of missing data are indicated by crosses.
3.Wind-Related Processes Affecting SST and Surface Layer Heat Content
In this section we review the processes related to wind forcing that can affect
SST and surface layer heat content. Arguments are cast in terms of simple mixed
layer models [e.g.,
Niiler and Kraus, 1977; McPhaden,
1982], where it is assumed that the temperature and velocity are uniform
over some depth h. This is done for illustrative purposes only, since
our measurements will show that the assumption of vertical uniformity of temperature
variations is invalid in the western equatorial Pacific on the time scales we
consider. Nonetheless, the model is conceptually useful for guiding the analysis.
With the above assumption, one can write
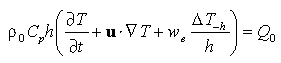 (1)
(1)
where  T/
T/ t is the
local time rate of temperature change, u is horizontal velocity, w
t is the
local time rate of temperature change, u is horizontal velocity, w , is an entrainment velocity through the base
of the mixed layer at depth z = -h, and Q
, is an entrainment velocity through the base
of the mixed layer at depth z = -h, and Q is surface heat flux. The horizontal temperature gradient
is denoted by
is surface heat flux. The horizontal temperature gradient
is denoted by 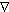 T, and
T, and  T
T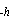 is the change in temperature at the base of the mixed layer. Water density (
is the change in temperature at the base of the mixed layer. Water density (
 ) and the heat
capacity of water at constant pressure (C
) and the heat
capacity of water at constant pressure (C )
are assumed constant at 10
)
are assumed constant at 10 kg m
kg m and 3.94 × 10
and 3.94 × 10 J kg
J kg °C
°C , respectively. Only
terms that can be readily related to the wind field (as discussed below) and can be
examined with our data sets have been retained in (1); other terms, namely, lateral
turbulent diffusion, vertical turbulent diffusion through the base of the mixed layer, and
penetrative solar radiation, have been neglected. These neglected terms may also depend on
wind forcing, though it is not obvious how, with out limited data set, we can critically
examine their relationship to SST and surface layer heat content.
, respectively. Only
terms that can be readily related to the wind field (as discussed below) and can be
examined with our data sets have been retained in (1); other terms, namely, lateral
turbulent diffusion, vertical turbulent diffusion through the base of the mixed layer, and
penetrative solar radiation, have been neglected. These neglected terms may also depend on
wind forcing, though it is not obvious how, with out limited data set, we can critically
examine their relationship to SST and surface layer heat content.
3.1. Turbulent Heat Exchange at the Surface
Surface heat exchange Q is made
up of longwave and shortwave radiative fluxes plus sensible and latent turbulent heat
fluxes. Bulk parameterizations of the turbulent heat fluxes are given by
is made
up of longwave and shortwave radiative fluxes plus sensible and latent turbulent heat
fluxes. Bulk parameterizations of the turbulent heat fluxes are given by
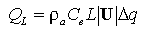 (2a)
(2a)
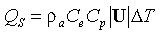 (2b)
(2b)
where |U| is wind speed,  q
is an air-sea specific humidity difference,
q
is an air-sea specific humidity difference,  T
is an air-sea temperature difference, C
T
is an air-sea temperature difference, C is a turbulent exchange coefficient,
is a turbulent exchange coefficient, 
 (= 1.2 kg m
(= 1.2 kg m ) is air density, and L
(= 2440 J g
) is air density, and L
(= 2440 J g ) is the latent heat of evaporation.
Wind speed dependence is explicit in these expressions; in addition, exchange
coefficients may depend on wind speed [e.g.,
Large and Pond, 1982]. Latent heat fluxes with monthly mean values
up to 100 W m
) is the latent heat of evaporation.
Wind speed dependence is explicit in these expressions; in addition, exchange
coefficients may depend on wind speed [e.g.,
Large and Pond, 1982]. Latent heat fluxes with monthly mean values
up to 100 W m are generally the larger of
the two turbulent fluxes in the western equatorial Pacific [e.g.,
Reed, 1985; Liu,
1988], so that most discussions of turbulent exchange focus on this
component alone.
are generally the larger of
the two turbulent fluxes in the western equatorial Pacific [e.g.,
Reed, 1985; Liu,
1988], so that most discussions of turbulent exchange focus on this
component alone.
Meyers
et al. [1986], using shipboard data, and Liu
[1988], using satellite data, have shown that during the 1982-1983 ENSO,
latent heat flux variations on monthly time scales were highly correlated with
wind speed variations in the western equatorial Pacific. However, these studies
differed in their conclusion about the relative importance of latent heat fluxes
in the surface temperature balance. Liu found little correlation between these
fluxes and SST variability along the equator; in contrast, Meyers et al. suggested
that a net 1°C cooling of the western Pacific warm pool during 1982-1983 resulted
from large latent heat fluxes associated with two episodes of strong equatorward
meridional winds during mid-1982 (southern winter) and early 1983 (northern
winter). The reason for these conflicting conclusions is unclear.
In a study that utilized many of the same time series data presented here,
McPhaden
et al. [1990] noted that high wind speed variations on weekly to monthly
time scales during the 1986-1987 ENSO were associated with cool SST near the
equator. This led to a suggestion that there existed a relationship between
variations in latent heat flux and surface cooling on these time scales. However,
McPhaden et al. did not quantify the suggested relationship between SST and
wind speed in support of this hypothesis.
3.2. Vertical Advection and Entrainment
Vertical advection and entrainment are related but distinct processes involved in
changing surface layer heat content and SST. Their combined effect during periods of
easterly winds is often referred to as equatorial upwelling. Entrainment velocity w can be written as
can be written as
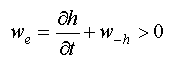 (3)
(3)
where w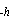 is vertical velocity at
the base of the surface layer and
is vertical velocity at
the base of the surface layer and  h/
h/ t is the local time rate of change of the surface layer
thickness. The inequality implies that in a stably stratified ocean, entrainment can only
cool the surface. The velocity w
t is the local time rate of change of the surface layer
thickness. The inequality implies that in a stably stratified ocean, entrainment can only
cool the surface. The velocity w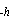 is sometimes inferred from the vertical displacement of isotherms in the thermocline
(assuming the effects of turbulent diffusion and lateral advection can be ignored).
Processes contributing to w
is sometimes inferred from the vertical displacement of isotherms in the thermocline
(assuming the effects of turbulent diffusion and lateral advection can be ignored).
Processes contributing to w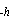 are
tides; small-scale, high-frequency internal waves; equatorial waves; and Ekman pumping due
to local wind-driven variations in horizontal mass convergence and divergence. When Ekman
dynamics are operative, w
are
tides; small-scale, high-frequency internal waves; equatorial waves; and Ekman pumping due
to local wind-driven variations in horizontal mass convergence and divergence. When Ekman
dynamics are operative, w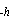 on the
equator will be proportional to the local zonal wind stress
on the
equator will be proportional to the local zonal wind stress
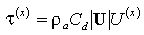 (4)
(4)
where C is a drag coefficient and U
is a drag coefficient and U is zonal wind speed.
is zonal wind speed.
In the limit where h is a constant, entrainment velocity is just the vertical
velocity at the base of the mixed layer. Under these circumstances, thermocline
displacements (given the assumptions above) and SST would be in phase and highly
correlated. Conversely, in the limit where the base of the mixed layer is a material
surface (that is, w = 0), the mixed
layer depth would change coherently with changes in thermocline depth and there would be
no effect of entrainment on SST.
= 0), the mixed
layer depth would change coherently with changes in thermocline depth and there would be
no effect of entrainment on SST.
Entrainment can also be parameterized in terms of the surface layer turbulent
energy balance [Niiler
and Kraus, 1977; McPhaden,
1982]. Two sources of turbulent energy production directly related to
the wind field are wind work (proportional to wind speed cubed) and free convection
due to heat loss by evaporation and conduction (proportional to wind speed).
The role of free convection cannot be evaluated without taking into account
surface buoyancy fluxes caused by radiative heating and precipitation. On the
other hand, the effect of wind work, which is always a source of turbulent energy
production, can be expressed by
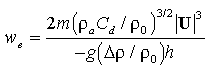 (5)
(5)
where 
 is
the density jump across the base of the mixed layer, g is gravity, and
m is an empirically determined efficiency factor [Niiler
and Kraus, 1977]. Note that the efficiency of entrainment decreases
as layer depth increases because, for a given wind speed, more of the water
column has to be energized with turbulence. Other sources of turbulent energy
production may enhance this entrainment (for example, production by vertical
shear instability at the base of the mixed layer), but they can not be reliably
estimated from our data set.
is
the density jump across the base of the mixed layer, g is gravity, and
m is an empirically determined efficiency factor [Niiler
and Kraus, 1977]. Note that the efficiency of entrainment decreases
as layer depth increases because, for a given wind speed, more of the water
column has to be energized with turbulence. Other sources of turbulent energy
production may enhance this entrainment (for example, production by vertical
shear instability at the base of the mixed layer), but they can not be reliably
estimated from our data set.
The role of entrainment mixing in the heat balance of the western equatorial
Pacific was discussed by Meyers
et al. [1986], who concluded that its effect on SST during the 1982-1983
ENSO was relatively small. McPhaden
et al. [1990] found evidence for equatorial upwelling (that is, upward
advection and entrainment) during a period of strong easterly winds at 165°E
in early 1988. However, based on the incoherence of SST and thermocline depth
variations (as measured by the depth of the 20°C isotherm over a period of 2.5
years during 1986-1988), they inferred that, in general entrainment of cold
waters from the thermocline was not important in determining SST variability
in the western equatorial Pacific. They suggested that this was owing to the
relatively thick (50-100 m) surface layer and the fact that it was not always
completely mixed with regard to temperature or salinity. Lukas
and Lindstrom [this issue] and Godfrey
and Lindstrom [1989] have hypothesized that the existence of a salt-stratified
"barrier layer" in the temperature mixed layer inhibits entrainment
in the western equatorial Pacific except during infrequent, large-amplitude
westerly wind bursts. However, in none of these studies was the relationship
between SST, surface layer heat content, and wind work according to (5)
examined.
3.3. Lateral Advection
Another process that can cause SST to change is lateral advection. This is
represented by the term u · 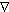 T
in (1), which assumes slablike flow over the layer
depth h. Whereas this is not strictly valid in the warm-pool region of
the western Pacific, a significant component of flow is depth coherent in the
surface layer [e.g.,
McPhaden et al., 1988]. Moreover, for a purely advective balance,
T
in (1), which assumes slablike flow over the layer
depth h. Whereas this is not strictly valid in the warm-pool region of
the western Pacific, a significant component of flow is depth coherent in the
surface layer [e.g.,
McPhaden et al., 1988]. Moreover, for a purely advective balance,
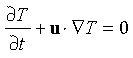 (6)
(6)
which can be tested with data from a single depth.
4. Structure of Temperature and Wind Variations
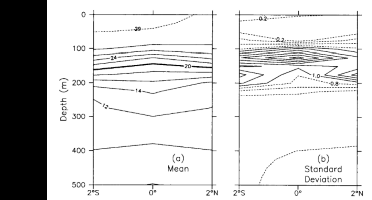
Fig. 4. (a) Mean and (b) standard deviation of temperature between
2°N and 2°S, 165°E for December 13, 1986 to April 16, 1987. Contour interval in Figure
4a is 2°C (except for the 29°C isotherm shown as a dashed line); contour interval
in Figure 4b is 0.2°C, with contours less than 1°C dashed.
Figure 4a shows the mean meridional temperature
section between 2°N and 2°S along 165°E for the period from December 1986 to April
1987, which is the longest period of overlapping data at the three mooring sites. Mean SST
is near to or greater than 29°C during this time. The surface layer is nearly isothermal,
with a mean vertical temperature difference in the upper 50-75 m at each of three
locations of about 0.2°C. The thermocline is centered between 100-200 m, with equatorial
weakening indicative of the presence of the Equatorial Undercurrent. Note that during the
second half of the record the upper thermocline is weaker and the surface layer is
shallower because of an abrupt shoaling of the 24°-28°C isotherms in late May 1987 (Figure 3).
Figure 4b shows that the largest temperature
variations (standard deviation 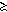 2°C) are found in the
thermocline on the equator between 100 and 150 m. Conversely, temperature variations in
the surface layer are typically only 0.1°-0.3°C. Notably, SST variations tend to be
larger than those at 50 m, which is a point that will be discussed in detail in section 5.
2°C) are found in the
thermocline on the equator between 100 and 150 m. Conversely, temperature variations in
the surface layer are typically only 0.1°-0.3°C. Notably, SST variations tend to be
larger than those at 50 m, which is a point that will be discussed in detail in section 5.
Figure 5 shows the first two empirical orthogonal
eigenfunctions (EOFs) for temperature data summarized in Figure
4. Variations associated with these eigenfunctions are determined by multiplication
of the EOFs with their corresponding time series. EOFs are defined to be orthogonal
and the time series uncorrelated [Davis,
1976]; as such, they are an efficient means of isolating coherent modes
of variability in large data sets.
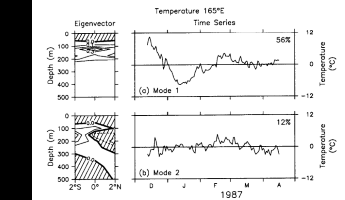
Fig. 5. (a) Temperature empirical orthogonal eigenfunctions (EOF) mode 1 and
(b) mode 2 for the period December 13, 1986, to April 16, 1987. Percent variance
explained by each EOF is indicated. Hatching indicates negative eigenvector values.
The first EOF (Figure 5a) accounts for
56% of the temperature variance and is similar in structure to the total variability
shown in Figure 4b, that is, the largest
variance is on the equator in the thermocline. Variations are in phase in latitude
by out of phase between the surface layer and the thermocline. The second EOF
(Figure 5b), which accounts for 12% of
the variance, shows a latitudinally antisymmetric mode of variability in the
thermocline. In combination with meridional wind and velocity measurements from
the 165°E moorings (including those shown in Figures
2b and 14), Hayes
et al. [1988] interpreted this structure in terms of a first baroclinic
mode mixed Rossby-gravity wave, with a dominant period near 10 days. Hence in
this analysis we will focus mainly on the first EOF, which accounts for most
of the temperature variability during the period from December 1986 to April
1987.
We also performed an EOF decomposition of the overlapping wind record from December
1986 to April 1987 in Figure 2. Only the first EOF is
shown, since it accounts for 77% (55%) of the variance in the zonal (meridional)
directions (Figure 6). The first zonal wind EOF indicates
in-phase variations of comparable amplitude across 2°N-2°S and a low-frequency variation
that is similar to that shown in Figure 5a for the
first temperature EOF. The cross-correlation coefficient for these two time series (0.54)
is significantly nonzero, with 95% confidence. In contrast, the first meridional wind EOF
has most of its variance concentrated at 2°S, and its correlation with the first
temperature EOF is not significant at the 95% level of confidence.
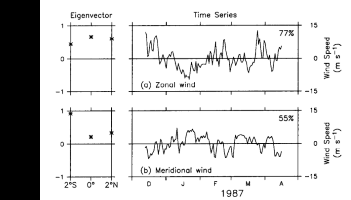
Fig. 6. Mode 1 wind EOFs for the period December 13, 1986, to April 16, 1987, in (a)
the zonal direction and (b) the meridional direction. Percent variance explained by
each EOF is indicated.
These results indicate that westerly winds (relative to the mean) are associated with
warm thermocline temperatures and that easterly winds (relative to the mean) are
associated with cold thermocline temperatures, a relationship similar to that expected for
Ekman pumping. However, the out-of-phase relationship between surface layer temperature
and thermocline temperature shown in Figure 5a
suggests that wind-driven vertical advection of the thermocline may not be a significant
factor in changing SST. This issue is examined in greater detail in section 5, where the
analysis focuses on the longer equatorial mooring record with its finer vertical
resolution in the surface layer.
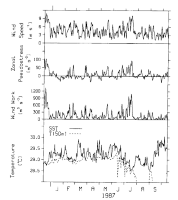
Fig. 7. Time series of daily averaged wind speed (|U|), zonal wind pseudostress (|U|U ), wind pseudowork (|U|
), wind pseudowork (|U| ), SST, and temperature at 50 m (dashed curve) from the
current meter mooring at 0°, 165°E for the period December 13, 1986, to October 14,
1987. Note that 50-m temperatures are off-scale frequently after August 1987 because the
upper thermocline has risen to this depth by then (see Figure 3).
), SST, and temperature at 50 m (dashed curve) from the
current meter mooring at 0°, 165°E for the period December 13, 1986, to October 14,
1987. Note that 50-m temperatures are off-scale frequently after August 1987 because the
upper thermocline has risen to this depth by then (see Figure 3).
5. Surface Turbulent Fluxes, Vertical Advection, and Entrainment
Figure 7 shows time series of wind speed (|U|),
zonal wind pseudostress (|U|U ), and
pseudowork (|U|
), and
pseudowork (|U| ) from the mooring at 0°, 165°E
for December 1986 to October 1987. In each case, estimates were first computed from hourly
data, then averaged to daily values. Ignoring the weak wind speed dependence of C
) from the mooring at 0°, 165°E
for December 1986 to October 1987. In each case, estimates were first computed from hourly
data, then averaged to daily values. Ignoring the weak wind speed dependence of C and C
and C for the range of speeds shown in Figure 7, turbulent air-sea heat exchange will be proportional
to |U|, Ekman pumping proportional to |U|U
for the range of speeds shown in Figure 7, turbulent air-sea heat exchange will be proportional
to |U|, Ekman pumping proportional to |U|U , and wind work proportional to |U|
, and wind work proportional to |U| . The SST and 50-m temperature from the equatorial mooring
are also shown in Figure 7.
. The SST and 50-m temperature from the equatorial mooring
are also shown in Figure 7.
If your browser cannot view the following table correctly, click this
link for a GIF image of Table 1.
TABLE 1. Summary of Means and Standard Deviations for Wind Speed,
Zonal Wind
Pseudostress, Pseudowork, and Sea Surface Temperature From the Current Meter
Mooring at 0°, 165°E for the Period From December 13, 1986, to October 14, 1987
|
|
Wind |
Zonal |
|
|
|
|
Speed |
Pseudostress, |
Pseudowork, |
SST, |
T(50 m), |
|
m s |
m² s |
m³ s |
°C |
°C |
|
| Mean |
4.5 |
9.7 |
184 |
29.2 (29.2) |
(29.0) |
| Standard deviation |
2.0 |
24.8 |
227 |
0.31 (0.22) |
(0.11) |
|
Numbers in parentheses for SST and T(50 m) are
statistics for December 13, 1986 to May 31, 1987,
when the surface layer extended to at least 50-m depth. |
Table 1 summarizes the means
and standard deviations of the time series in Figure 7. The
mean wind speed is only 4.5 m s and the mean zonal
pseudostress is eastward at 9.7 m
and the mean zonal
pseudostress is eastward at 9.7 m s
s (for a constant C
(for a constant C of 1.2 × 10
of 1.2 × 10 , this
pseudostress translates into a mean zonal stress of about 0.014 N m
, this
pseudostress translates into a mean zonal stress of about 0.014 N m ). Standard deviations in both of these variables are also
small: 2.0 m s
). Standard deviations in both of these variables are also
small: 2.0 m s for |U| and 24.8 m
for |U| and 24.8 m s
s for |U|U
for |U|U (equivalent to 0.036 N m
(equivalent to 0.036 N m ). SST is high on average (29.2°C), with a standard
deviation of 0.31°C. Temperature at 50 m is 29.0°C on average, with a standard deviation
two times smaller than the SST standard deviation during the first part of the record,
when 50 m is located in the surface layer.
). SST is high on average (29.2°C), with a standard
deviation of 0.31°C. Temperature at 50 m is 29.0°C on average, with a standard deviation
two times smaller than the SST standard deviation during the first part of the record,
when 50 m is located in the surface layer.
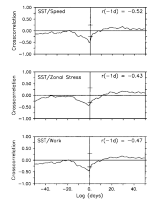
Fig. 8. Cross correlations between SST and wind speed, zonal wind pseudostress, and
wind pseudowork. Cross correlation extrema (r) and the lag (in days) at which they
occur are shown. In each case, the lag indicates that cold SST follows high winds by 1
day. The 95% confidence limits for the null hypothesis of uncorrelated variability are
indicated by horizontal bars on the abscissa.
Figure 8 indicates the cross correlations of the three
wind constructs with SST are significantly nonzero at the 95% level of confidence and
range between -0.43 (for zonal pseudostress) and -0.52 (for wind speed). The negative
correlation indicates that high wind speed, high wind work, and westerly wind stress
(relative to the mean) are associated with cool SST; low wind speed, low wind work, and
easterly wind stress (relative to the mean) are associated with warm SST. In each case the
maximum cross correlation occurs with SST lagging the winds by 1 day, consistent with the
atmosphere forcing the ocean on these time scales. Although not presented, the magnitude
of the cross correlation between meridional wind pseudostress and SST is generally  0.2 over the range of lags shown in Figure 8.
0.2 over the range of lags shown in Figure 8.
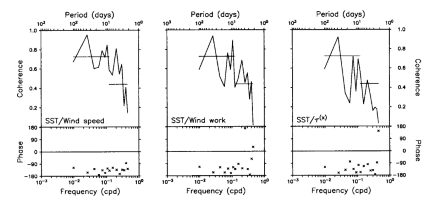
Fig. 9. Coherence and phase spectra for SST and wind speed, zonal wind pseudostress,
and wind pseudowork at 0°, 165°E for the period December 13, 1986, to October 14, 1987.
Positive phase indicates that high winds lead high SST, and negative phase indicates that
high winds lead low SST. Horizontal lines superimposed on coherence estimates indicate 95%
confidence limits for the null hypothesis of incoherent variability, based on five (15)
frequency band averages at periods longer (shorter) than about 8 days.
Another way to view these relationships is in the frequency domain. Figure
9 shows the coherence and phase as a function of frequency between the three
wind constructs and SST. Two bands of high and statistically significant coherence
are evident. These are at periods between approximately 3-8 days and 30-60 days;
to a lesser extent, variations at 10-20 days are also coherent. Consistent with
the cross-correlation statistics, the phase in most frequency bands is between
-90° and -180°, implying that maxima in the winds are followed by cold SST and
minima are followed by warm SST. Coherence at periods shorter than 20 days may
be related to westerly wind burst activity. Coherence at periods of 30-60 days
could be related to atmospheric fluctuations associated with Madden
and Julian [1972] waves.
Note that although there are differences between the coherence and phase diagrams in Figure 9 and the cross-correlation analysis summarized in Figure 8, the statistical relationships of the three wind
constructs with SST share many similarities; indeed, wind speed, zonal wind pseudostress,
and wind work are highly correlated among themselves (0.61-0.90). Hence without further
analysis one cannot unambiguously identify which of the processes related to the wind
field are most important in affecting SST.
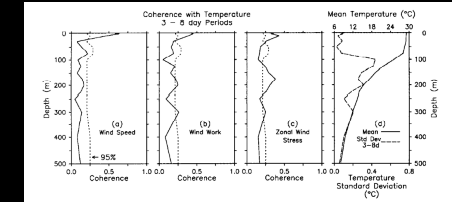
Fig. 10. Coherence amplitude as a function of depth averaged over periods of
approximately 3-8 days (encompassing 36-65 frequency bands depending on depth) for SST and
wind speed, zonal wind pseudostress, and wind pseudowork at 0°, 165°E. The 95%
confidence limits for the null hypothesis of incoherent variability are indicated by the
dashed lines. Note that the temperature record lengths for this analysis were chosen such
that the statistics were stationary; for example, the period June-October 1987 was
excluded at 50 m and 75 m. Shown on the right are the mean temperature profile (solid
curve) and the standard deviation of temperature variations at periods of approximately
3-8 days (dashed curve) for December 13, 1986, to October 14, 1987.
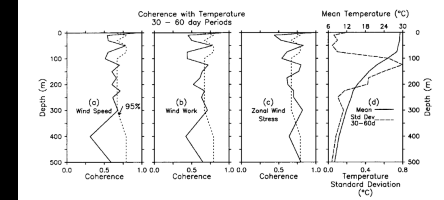
Fig. 11. Coherence amplitude as a function of depth averaged over periods of
approximately 30-60 days (that is 4-6 frequency bands, depending on depth) for SST and
wind speed, zonal wind pseudostress, and wind pseudowork at 0°, 165°E. The 95%
confidence limits for the null hypothesis of incoherent variability are indicated by the
dashed lines. Shown on the right are the mean temperature profile (solid curve) and the
standard deviation of temperature variations at periods of approximately 30-60 days
(dashed curve) for December 13, 1986, to October 14, 1987.
Figure 10 shows coherence amplitude as a function of
depth in the 3- to 8-day period band. Also shown in Figure 10
is the mean temperature profile for December 1986 to October 1987. Wind speed, wind
stress, and wind work are all significantly coherent with temperature variations between 1
and 10 m. Coherence drops rapidly below these depths, however, and is statistically
insignificant at the 95% level in the lower part of the surface layer between 50 and 75 m.
In the thermocline, wind speed and wind work are generally incoherent with temperature
fluctuations; on the other hand, zonal pseudostress shows a clear pattern of coherence
between 125 and 300 m. The coherence profiles for the 10- to 20-day and 30- to 60-day
period bands are generally similar to those shown in Figure 10.
Figure 11, for example, shows the coherence as a function
of depth for wind speed, zonal pseudostress, and wind work in the 30- to 60-day band. In
each case the coherence is high at the surface, then falls off rapidly to relatively low
and/or insignificant values. Only in the case of zonal pseudostress does significantly
nonzero coherence appear consistently in the thermocline.
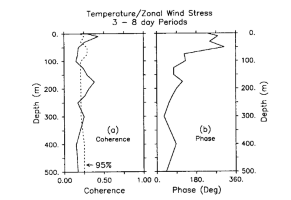
Fig. 12. Coherence amplitude and phase as a function of depth averaged over periods
of approximately 3-8 days (encompassing 36-65 frequency bands, depending on depth) for SST
and zonal wind pseudostress at 0°, 165°E. The 95% confidence limits for the null
hypothesis of incoherent variability are indicated by the dashed curve.
Figure 12 shows that the phase of zonal pseudostress
coherence in the 3- to 8-day band is such that warm thermocline temperatures lag relative
westerly winds by about 90° and cold thermocline temperatures lag relative easterly winds
by the same amount. This is consistent with the Ekman pumping hypothesis for thermocline
variations discussed in section 4. However, phase changes by 180° across the base of the
surface layer, indicating that temperature variations are of opposite sign in the surface
layer and thermocline. A similar phase change occurs at lower frequencies as well.
Vertical advection from the thermocline is therefore not likely to be the principal
mechanism controlling SST on these time scales, as was earlier suggested in the discussion
of Figure 5a. Likewise, the rapid decrease in
coherence with depth below 10 m in Figures 10 and 11 suggests that entrainment from the thermocline is not, in
general, important in controlling SST. One would expect coherence between temperature and
|U| to be much higher at 50-75 m if the
thermocline were the source of cold water for the surface layer. This leaves turbulent
surface fluxes proportional to |U| as the most likely candidate for affecting SST
and surface layer heat content.
to be much higher at 50-75 m if the
thermocline were the source of cold water for the surface layer. This leaves turbulent
surface fluxes proportional to |U| as the most likely candidate for affecting SST
and surface layer heat content.
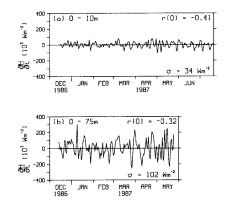
Fig. 13. Time series of  H/
H/ t for depth ranges of (a) 0-10 m for the period
December 13, 1986, to July 20, 1987, and (b) 0-75 m for the period December 13,
1986, to May 31, 1987. The standard deviation of heat content variations (
t for depth ranges of (a) 0-10 m for the period
December 13, 1986, to July 20, 1987, and (b) 0-75 m for the period December 13,
1986, to May 31, 1987. The standard deviation of heat content variations ( ) and cross correlation with wind speed at zero lag (r)
are shown.
) and cross correlation with wind speed at zero lag (r)
are shown.
Further evidence to support the role of wind-related surface turbulent heat flux
variations can be found in an examination of upper ocean heat content (defined as H
= pC hT) from the 0°, 165°E mooring.
Figure 13 shows time series of
hT) from the 0°, 165°E mooring.
Figure 13 shows time series of  H/
H/ t estimated using
centered differences over two depth ranges: 0-10 m (where coherence with the wind speed is
highest) and 0-75 m (the average depth of the surface layer). The calculation for 0-75 m
is shown only through the end of May 1987, because of the nonstationarity of the time
series during the second half of the record when the upper portion of the thermocline
reaches depths of 50-75 m (see Figures 3 and 7). The standard deviation of
t estimated using
centered differences over two depth ranges: 0-10 m (where coherence with the wind speed is
highest) and 0-75 m (the average depth of the surface layer). The calculation for 0-75 m
is shown only through the end of May 1987, because of the nonstationarity of the time
series during the second half of the record when the upper portion of the thermocline
reaches depths of 50-75 m (see Figures 3 and 7). The standard deviation of  H/
H/ t(
t( ) and the cross correlation at zero lag (r) of
) and the cross correlation at zero lag (r) of  H/
H/ t and |U| also
appear in Figure 13. For both depth ranges the cross
correlations are significantly nonzero (with 95% confidence) and are higher than for
either pseudostress or for wind work.
t and |U| also
appear in Figure 13. For both depth ranges the cross
correlations are significantly nonzero (with 95% confidence) and are higher than for
either pseudostress or for wind work.
Variations in heat content within the 0- to 75-m layer are 102 W m .
Multiplying this number by 0.32, that is, the magnitude of the correlation between
.
Multiplying this number by 0.32, that is, the magnitude of the correlation between
 H/
H/ t and
|U|, indicates that heat content changes of approximately 33 W m
t and
|U|, indicates that heat content changes of approximately 33 W m in the upper 75-m surface layer are due to wind speed variations. This estimate
is comparable to what would be expected for latent heat flux variations based
on (2a) and typical observed parameter
values. Specifically, Q
in the upper 75-m surface layer are due to wind speed variations. This estimate
is comparable to what would be expected for latent heat flux variations based
on (2a) and typical observed parameter
values. Specifically, Q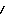
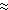 35 W m
35 W m for wind speed variations of 2.0 m s
for wind speed variations of 2.0 m s (Table
1), C
(Table
1), C , of 1.2 × 10
, of 1.2 × 10 [Large
and Pond, 1982] and a typical
[Large
and Pond, 1982] and a typical  q
of 5 g kg
q
of 5 g kg [Reed,
1985; Liu,
1988].
[Reed,
1985; Liu,
1988].
For comparison, the magnitude of variations in entrainment mixing due to wind
work can be estimated from (1) and (5),
using a scale analysis similar to that for latent heat flux. For |U| of 227 m
of 227 m s
s (Table 1), m
= 0.4 [Davis
et al., 1981; McPhaden,
1982], (
(Table 1), m
= 0.4 [Davis
et al., 1981; McPhaden,
1982], ( T/
T/ p)
p)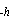 = 3°C m
= 3°C m kg
kg at the base of the surface layer (determined from conductivity-temperature-depth
(CTD) casts near 0°, 165°E), and h = 75 m, we find that
at the base of the surface layer (determined from conductivity-temperature-depth
(CTD) casts near 0°, 165°E), and h = 75 m, we find that 
 C
C w
w
 T
T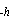 =5 W m
=5 W m . Other choices of m, h,
and (
. Other choices of m, h,
and ( T/
T/ p)
p)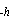 would result in different
estimates of entrainment from the thermocline; however, it is unlikely that
a reasonable combination of these parameters would increase our 5 W m
would result in different
estimates of entrainment from the thermocline; however, it is unlikely that
a reasonable combination of these parameters would increase our 5 W m estimate by an order of magnitude. Thus we conclude that latent heat flux variations
are significantly more important than wind work-related entrainment fluxes from
the thermocline in controlling SST and surface layer heat content during the
time period of this study.
estimate by an order of magnitude. Thus we conclude that latent heat flux variations
are significantly more important than wind work-related entrainment fluxes from
the thermocline in controlling SST and surface layer heat content during the
time period of this study.
A comparison of heat content variations over the 0- to 10-m layer and the 0-
to 75-m layer indicates that surface cooling associated with Q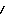 converges nonlinearly in the upper 75 m. The product of |r| and
converges nonlinearly in the upper 75 m. The product of |r| and 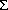 over the two depth ranges in Figure 13 implies
a standard deviation of 14 W m
over the two depth ranges in Figure 13 implies
a standard deviation of 14 W m and 33 W m
and 33 W m for wind-related heat content variations in the upper 10 m and 75 m, respectively.
The 19 W m
for wind-related heat content variations in the upper 10 m and 75 m, respectively.
The 19 W m difference between these two
flux estimates represents variability in the depth range 10-75 m. Thus 14 W
m
difference between these two
flux estimates represents variability in the depth range 10-75 m. Thus 14 W
m (42% of the total) converges in the upper
10 m (13% of the 75-m layer depth) whereas 19 W m
(42% of the total) converges in the upper
10 m (13% of the 75-m layer depth) whereas 19 W m (58% of the total) converges between 10 and 75 m (87% of the surface layer depth).
Using an integral time scale (t
(58% of the total) converges between 10 and 75 m (87% of the surface layer depth).
Using an integral time scale (t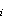 )
for wind-speed-related temperature variations of 3-4 days (based on the cross-correlation
analysis in Figure 8) and a
)
for wind-speed-related temperature variations of 3-4 days (based on the cross-correlation
analysis in Figure 8) and a  H/
H/ t
of 14 W m
t
of 14 W m (0-10 m) and 19 W m
(0-10 m) and 19 W m (10-75 m), we find the expected magnitude of temperature variations (T ~
t
(10-75 m), we find the expected magnitude of temperature variations (T ~
t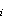
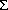 r/
r/ C
C h)
associated with latent heat flux variations in each of these depth ranges to
be about 0.1°C and 0.02°C, respectively. The latter temperature is close to
the instrumental accuracy of our temperature sensors [e.g.,
McPhaden et al., 1990] and probably accounts for the insignificant
temperature and wind coherences on a pointwise basis for depths greater than
10 m in the surface layer.
h)
associated with latent heat flux variations in each of these depth ranges to
be about 0.1°C and 0.02°C, respectively. The latter temperature is close to
the instrumental accuracy of our temperature sensors [e.g.,
McPhaden et al., 1990] and probably accounts for the insignificant
temperature and wind coherences on a pointwise basis for depths greater than
10 m in the surface layer.
6. Lateral Advection
Another possible candidate contributing to variations in SST and heat content
is lateral advection. A 50-m velocity record is the shallowest time series we
have in 1987 to test this hypothesis. However, as discussed by McPhaden
et al. [1990], daily averaged 10- and 50-m currents are highly correlated
(0.87 for 164 days of overlapping 1986 data), so that fluctuations at 50 m can
be used as an index of flow in the surface layer.
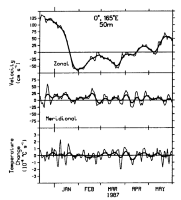
Fig. 14. Zonal velocity (u), meridional velocity (v), and time rate of
change of temperature ( T/
T/ T) at 50 m from December 13, 1986, to May 31, 1987, at 0°,
165°E. Daily averaged data are shown by thin curves and 15-day Hanning filtered data are
shown by thick curves.
T) at 50 m from December 13, 1986, to May 31, 1987, at 0°,
165°E. Daily averaged data are shown by thin curves and 15-day Hanning filtered data are
shown by thick curves.
Velocity at 50 m is shown in Figure 14 for that
time period when the 50-m depth is located in the surface layer (see Figure
3). Flow in the zonal direction is strongly eastward at speeds greater than
100 cm s in December 1986, westward at speeds
up to 70 cm s
in December 1986, westward at speeds
up to 70 cm s from late January to early
April 1987, then eastward again beginning in mid-April. The range of zonal speeds
in these month-to-month measurements is about 200 cm s
from late January to early
April 1987, then eastward again beginning in mid-April. The range of zonal speeds
in these month-to-month measurements is about 200 cm s .
Meridional velocities vary at periods near 10 days with peak-to-peak amplitudes
of 50-100 cm s
.
Meridional velocities vary at periods near 10 days with peak-to-peak amplitudes
of 50-100 cm s ; these fluctuations are
associated with the second temperature EOF (Figure
5b) and are related to mixed Rossby-gravity wave dynamics [Hayes
et al., 1988]. Velocity variations in both directions are in part forced
by local winds, as discussed by McPhaden
et al. [1990] and Hayes
et al. [1988].
; these fluctuations are
associated with the second temperature EOF (Figure
5b) and are related to mixed Rossby-gravity wave dynamics [Hayes
et al., 1988]. Velocity variations in both directions are in part forced
by local winds, as discussed by McPhaden
et al. [1990] and Hayes
et al. [1988].
Figure 14 also shows the centered difference equivalent
of  T/
T/ t, variations
of which would be highly correlated with one or both of the velocity components if lateral
advection were dominant in the temperature balance. In addition, according to (6), one would be able to estimate the time-averaged horizontal
temperature gradient by regressing velocity against
t, variations
of which would be highly correlated with one or both of the velocity components if lateral
advection were dominant in the temperature balance. In addition, according to (6), one would be able to estimate the time-averaged horizontal
temperature gradient by regressing velocity against  T/
T/ t. However, cross correlations of daily averaged zonal
velocity (u) and meridional velocity (v) with
t. However, cross correlations of daily averaged zonal
velocity (u) and meridional velocity (v) with  T/
T/ t are only 0.05 and 0.17,
respectively, neither of which exceeds the 95% confidence limits for the null hypothesis
of 0.11 in the zonal direction and 0.26 in the meridional direction. We repeated these
calculations for data smoothed with a 15-day Hanning filter (approximately equivalent to
computing weekly averages). As shown in Figure 14, there
are times such as early March to mid-April when the low-pass
t are only 0.05 and 0.17,
respectively, neither of which exceeds the 95% confidence limits for the null hypothesis
of 0.11 in the zonal direction and 0.26 in the meridional direction. We repeated these
calculations for data smoothed with a 15-day Hanning filter (approximately equivalent to
computing weekly averages). As shown in Figure 14, there
are times such as early March to mid-April when the low-pass  T/
T/ t and meridional velocity
track reasonably closely. Overall however, the cross correlations for the 15-day Hanning (u,
t and meridional velocity
track reasonably closely. Overall however, the cross correlations for the 15-day Hanning (u,
 T/
T/ t) and (v,
t) and (v,  T/
T/ t) data are 0.14 and
0.23, neither of which exceeds the 95% confidence limits of 0.34 and 0.38 for the low-pass
time series. We repeated these calculations for
t) data are 0.14 and
0.23, neither of which exceeds the 95% confidence limits of 0.34 and 0.38 for the low-pass
time series. We repeated these calculations for  T/
T/ t computed from SST and from temperature averaged over 0-10
m and 0-75 m, assuming that the 50-m currents were representative of depth-averaged flow
in the surface layer. No clear pattern of significant cross correlation emerged, implying
that, in general, lateral advection has a negligible effect on surface layer temperature
variability on daily to monthly time scales for the period of this study. This is
consistent with a mean temperature field characterized by weak horizontal gradients in the
vicinity of 0°, 165°E during much of 1987 (for example, Figure
1).
t computed from SST and from temperature averaged over 0-10
m and 0-75 m, assuming that the 50-m currents were representative of depth-averaged flow
in the surface layer. No clear pattern of significant cross correlation emerged, implying
that, in general, lateral advection has a negligible effect on surface layer temperature
variability on daily to monthly time scales for the period of this study. This is
consistent with a mean temperature field characterized by weak horizontal gradients in the
vicinity of 0°, 165°E during much of 1987 (for example, Figure
1).
7. Summary and Discussion
The foregoing analysis has focused on a diagnosis of the surface layer heat balance
using equatorial mooring data along 165°E during 1986 and 1987. Several processes related
to wind forcing were examined, using statistical relationships between winds, temperature,
and currents. We found that among the processes considered, evaporative cooling was the
most important, accounting for heat content changes of typically 35 W m in the upper 75 m. Moreover, these evaporative heat fluxes
converged nonuniformly in the surface layer, giving rise to temperature variations of
about 0.1°C in the upper 10 m, but only about 0.02°C between 10 and 75 m. Entrainment
from the thermocline due to wind work was an order of magnitude smaller. In addition, the
affects of lateral advection were not significant, in spite of large (50-100 cm s
in the upper 75 m. Moreover, these evaporative heat fluxes
converged nonuniformly in the surface layer, giving rise to temperature variations of
about 0.1°C in the upper 10 m, but only about 0.02°C between 10 and 75 m. Entrainment
from the thermocline due to wind work was an order of magnitude smaller. In addition, the
affects of lateral advection were not significant, in spite of large (50-100 cm s ) velocity fluctuations in the surface layer. This is
because the horizontal temperature gradients were weak near 0°, 165°E during the time
period of our analysis.
) velocity fluctuations in the surface layer. This is
because the horizontal temperature gradients were weak near 0°, 165°E during the time
period of our analysis.
The inferred nonuniform convergence of evaporative heat flux in the surface
layer, the weak temperature variations at 50 m relative to those at the surface
(for example, Figure 7), and the weakness of
wind work entrainment from the thermocline indicate that some process or combination
of processes significantly limits the vertical extent to which heat can be mixed
in the western Pacific warm pool. One possibility is the formation of a salt-stratified
barrier layer, as suggested by Lukas
and Lindstrom [this issue] and Godfrey
and Lindstrom [1989]. Although we do not have salinity time series from
the period of our analysis to test this hypothesis quantitatively, CTD data
along 165°E show the existence of shallow, 0- to 10-m thick lenses of low-salinity
water, with surface values up to 1 psu (practical salinity unit) lower than
normal. These may be related to enhanced precipitation associated with an eastward
displacement of deep convection across 165°E during the 1986-1987 ENSO. It has
yet to be determined, however, whether the haloclines associated with these
buoyant lenses are sufficiently strong to trap heat in a shallow layer near
the surface.
Another possibility is that formation of the diurnal thermocline may be involved
in limiting the depth penetration of heat on longer time scales. Daytime radiative
heating leads to typical diurnal temperature variations of O(0.1°C) in
the upper 10 m of the western equatorial Pacific [Taft
and McPhaden, 1988]. The amplitude of the diurnal cycle is related to
wind speed in qualitatively the same manner in which daily averaged SST is related
to wind speed, that is, the diurnal cycle is weak when wind speed is high (>6
m s ) and strong (>1°C) during periods
of calm winds. Wind speed was greater than 6 m s
) and strong (>1°C) during periods
of calm winds. Wind speed was greater than 6 m s for 22% of the time during the period from December 1986 to October 1987; however,
most of the time the winds were not strong enough to erode the diurnal thermocline
at the mooring site. One-dimensional mixed layer models indicate that inclusion
of the diurnal heating cycle quenches convection during the day, which leads
to shallower mixed layer depths than would be otherwise expected without the
diurnal cycle because of nonlinearities in the turbulent energy balance [Woods
and Barkmann, 1986]. Moreover, in the eastern equatorial Pacific Imawaki
et al. [1988] have shown that the diurnal cycle modulates the turbulent
heat flux out of the surface layer on longer time scales. Most of the turbulence
and mixing there occurs at night in association with free convection [Peters
et al., 1988]. Hence if formation of the diurnal thermocline were inhibited,
nighttime convection could start sooner, last longer, be more intense, and penetrate
to greater depths, resulting in a larger net downward heat flux. Conversely,
if the winds were weak during the day and the diurnal thermocline strong, nighttime
convection could be delayed, of shorter duration, weaker, and less vertically
penetrative.
for 22% of the time during the period from December 1986 to October 1987; however,
most of the time the winds were not strong enough to erode the diurnal thermocline
at the mooring site. One-dimensional mixed layer models indicate that inclusion
of the diurnal heating cycle quenches convection during the day, which leads
to shallower mixed layer depths than would be otherwise expected without the
diurnal cycle because of nonlinearities in the turbulent energy balance [Woods
and Barkmann, 1986]. Moreover, in the eastern equatorial Pacific Imawaki
et al. [1988] have shown that the diurnal cycle modulates the turbulent
heat flux out of the surface layer on longer time scales. Most of the turbulence
and mixing there occurs at night in association with free convection [Peters
et al., 1988]. Hence if formation of the diurnal thermocline were inhibited,
nighttime convection could start sooner, last longer, be more intense, and penetrate
to greater depths, resulting in a larger net downward heat flux. Conversely,
if the winds were weak during the day and the diurnal thermocline strong, nighttime
convection could be delayed, of shorter duration, weaker, and less vertically
penetrative.
Lukas
and Lindstrom [this issue] have suggested that repeated westerly wind
burst forcing associated with ENSO may lead to long-period, interannual cooling
of the western Pacific warm pool through wind work-generated entrainment mixing
with the thermocline. As noted above, entrainment does not appear to be important
in general along 165°E during 1987 at the height of the ENSO. Moreover, visually
and by least squares analysis, there is no significant SST cooling trend over
the record length shown in Figure 7, even though
several 5-10 m s westerly wind events occur
during this time period. In addition, the mean SST for December 1986 to October
1987 was not significantly colder than climatology (Figure
1); specifically, SST was 29.2°C (plus or minus one standard error of 0.1°C)
at 0°, 165°E compared to a climatological mean over the same time period of
29.0°C [Reynolds,
1988]. Thus while we have shown that short-period westerly wind fluctuations
lead to local SST variability on the same time scale, there is no evidence from
our data that they lead to local low-frequency SST cooling associated with ENSO.
Whether this result applies to other locations in the western equatorial Pacific
as well is not clear.
westerly wind events occur
during this time period. In addition, the mean SST for December 1986 to October
1987 was not significantly colder than climatology (Figure
1); specifically, SST was 29.2°C (plus or minus one standard error of 0.1°C)
at 0°, 165°E compared to a climatological mean over the same time period of
29.0°C [Reynolds,
1988]. Thus while we have shown that short-period westerly wind fluctuations
lead to local SST variability on the same time scale, there is no evidence from
our data that they lead to local low-frequency SST cooling associated with ENSO.
Whether this result applies to other locations in the western equatorial Pacific
as well is not clear.
Our conclusions with regard to advection and evaporation rely primarily on
inference, because we do not have specific humidity to calculate latent heat
flux, nor do we have accurate enough information on horizontal temperature gradients
to estimate advection explicitly. In addition, our estimate of 5 m as a typical entrainment heat flux based on wind work is only approximate, because
we do not have the data to incorporate into our estimate the affects of other
sources and sinks of turbulent energy (for example, buoyancy forcing due to
insolation and precipitation; vertical shear instability, etc.). Because of
these and other data limitations, we have been able to account for only about
10-25% of the observed SST and heat content variance in terms of evaporative
cooling, based on correlations with wind speed of 0.3-0.5 (for example, Figures
8 and 13). Shortwave radiation is likely
to account for a large percentage of the unexplained temperature variance in
the surface layer. Insolation at the equator under clear-sky conditions ranges
between about 300 and 350 W m
as a typical entrainment heat flux based on wind work is only approximate, because
we do not have the data to incorporate into our estimate the affects of other
sources and sinks of turbulent energy (for example, buoyancy forcing due to
insolation and precipitation; vertical shear instability, etc.). Because of
these and other data limitations, we have been able to account for only about
10-25% of the observed SST and heat content variance in terms of evaporative
cooling, based on correlations with wind speed of 0.3-0.5 (for example, Figures
8 and 13). Shortwave radiation is likely
to account for a large percentage of the unexplained temperature variance in
the surface layer. Insolation at the equator under clear-sky conditions ranges
between about 300 and 350 W m . Using Reed's
[1977] flux formula, changes in cloudiness of only 10% would lead to changes
in the net shortwave radiation at the sea surface of about 20 W m
. Using Reed's
[1977] flux formula, changes in cloudiness of only 10% would lead to changes
in the net shortwave radiation at the sea surface of about 20 W m .
Changes in cloudiness of this magnitude are likely to occur on daily to monthly
time scales, given that normally the skies are 60-70% cloud-covered owing to
very active deep convection in the western equatorial Pacific.
.
Changes in cloudiness of this magnitude are likely to occur on daily to monthly
time scales, given that normally the skies are 60-70% cloud-covered owing to
very active deep convection in the western equatorial Pacific.
In conclusion, we note that the SST changes observed in our mooring data are
only O(0.1°C). This is an order of magnitude smaller than those seen
in the eastern equatorial Pacific, where O(1°C) fluctuations on daily
to interannual time scales are common [e.g.,
McPhaden and Hayes, 1990]. It is encouraging that in spite of these
small temperature signals and our limited data set, we have been able to draw
inferences about physical processes at work in the surface layer heat balance.
We emphasize that these inferences are specific to the time period and location
of this study. Entrainment from the thermocline, for example, could be more
important during periods of strong upwelling favorable easterly winds. Likewise,
lateral advection could be important during periods when horizontal SST gradients
are pronounced, or on longer time scales (e.g. interannual) than those considered
in this study. Our analysis emphasizes the need, therefore, for longer and more
complete data sets in future investigations of air-sea interaction in the western
equatorial Pacific.
Acknowledgments. We would like to thank Stuart Godfrey of CSIRO, Hobart,
Australia, for helpful comments on an earlier version of this manuscript. We would also
like to acknowledge M. McCarty and H.P. Freitag for their assistance in carrying out the
analyses. This work was supported by the U.S. Tropical Ocean-Global Atmosphere (TOGA)
Project Office. Contribution 1166 from the Pacific Marine Environmental Laboratory,
National Oceanic and Atmospheric Administration.
References
Davis, R. E., Predictability of sea surface temperature and sea level pressure
anomalies over the North Pacific Ocean, J. Phys. Oceanogr., 6, 249-266, 1976.
Davis, R. E., R. De Szoerke, and P. P. Niiler, Variability in the upper ocean during
MILE, II, Modeling the mixed layer response, Deep Sea Res., 28, 1453-1476, 1981.
Freitag, H. P., M. J. McPhaden, and A. J. Shepherd, Equatorial current and temperature
data: 108°W to 110°W; October 1979 to November 1983, NOAA Data Rep., ERL PMEL-17, 99
pp., Environ. Res. Lab., Natl. Oceanic and Atmos. Admin., Boulder, Colo., 1987.
Godfrey, J. S., and E. J. Lindstrom, The heat budget of the equatorial western Pacific
surface mixed layer, J. Geophys. Res., 94, 8007-8017, 1989.
Hayes, S. P., L. J. Mangum, M. J. McPhaden, and J. Picaut, Thermal structure
variability along 165°E, paper presented at Symposium on Western Tropical Pacific Air-Sea
Interactions, U.S. TOGA Project Office, Beijing, China, Nov. 15-17, 1988.
Imawaki, S., P. P. Niiler, C. H. Gautier, D. Halpern, R. A. Knox, W. G. Large, D. S.
Luther, J. C. McWilliams, J. N. Moum, and C.A. Paulson, A new method for estimating the
turbulent heat flux at the bottom of the daily mixed layer, J. Geophys. Res., 93,
14,005-14,012, 1988.
Kousky, V. E., and A. Leetmaa, The 1986-87 Pacific warm episode: Evolution of oceanic
and atmospheric anomaly fields, J. Clim., 2, 254-267, 1989.
Large, W. G., and S. Pond, Sensible and latent heat fluxes over the ocean, J. Phys.
Oceanogr., 12, 464-482, 1982.
Liu, W. T., Moisture and latent heat flux variabilities in the tropical Pacific derived
from satellite data, J. Geophys. Res., 93, 6749-6760, 1988.
Lukas, R., and E. Lindstrom, The mixed layer of the western equatorial Pacific Ocean, J.
Geophys. Res., this issue.
Madden, R. A., and P. Julian, Description of global scale circulation cells in the
tropics with a 40-50 day period, J. Atmos. Sci., 29, 1109-1123, 1972.
McPhaden, M. J., Variability in the central equatorial Indian Ocean, II, Oceanic heat
and turbulent energy balances, J. Mar. Res., 40, 403-419, 1982.
McPhaden, M. J., On the relationship between winds and upper ocean temperature
variability in the western equatorial Pacific, in Proceedings of the Western Pacific
International Meeting and Workshop on TOGA-COARE, edited by J. Picaut, R. Lukas, and
T. Delcroix, pp. 283-290, ORSTOM, Noumea, New Caledonia, 1989.
McPhaden, M. J., H. P. Freitag, S. P. Hayes, B. A. Taft, Z. Chen, and K. Wyrtki, The
response of the equatorial Pacific Ocean to a westerly wind burst in May 1986, J.
Geophys. Res., 93, 10,589-10,603, 1988.
McPhaden, M. J., S. P. Hayes, L. J. Mangum, and J. Toole, Variability in the western
equatorial Pacific during the 1986-87 El Niño/Southern Oscillation event, J. Phys.
Oceanogr., 20, 190-208, 1990.
McPhaden, M. J., and S. P. Hayes, Variability in the eastern equatorial Pacific Ocean
during 1986-1988, J. Geophys. Res., 95, 13,195-13,208, 1990.
Meyers, G., J.-R. Donguy, and R. K. Reed, Evaporative cooling of the western equatorial
Pacific Ocean by anomalous winds, Nature, 323, 523-526, 1986.
Nicholls, N., Impact of the Southern Oscillation on Australian crops, J. Climatol.,
5, 553-560, 1985.
Niiler, P. P., and E. B. Kraus, One-dimensional models of the upper ocean, in Modelling
and Prediction of the Upper Layers of the Ocean, edited by E. B. Kraus, pp. 143-172,
Pergamon, New York, 1977.
Palmer, T. N., and D. A. Mansfield, Response of two atmospheric general circulation
models to sea-surface temperature anomalies in the tropical east and west Pacific, Nature,
310, 483-488, 1984.
Peters, H., M. C. Gregg, and J. M. Toole, On the parameterization of equatorial
turbulence, J. Geophys. Res., 93, 1199-1218, 1988.
Rasmusson, E. M., and J.M. Wallace, Meteorological aspects of the El Niño/Southern
Oscillation, Science, 222, 1195-2002, 1983.
Reed, R. K., On estimating insolation over the ocean, J. Phys. Oceanogr., 7, 482-485,
1977.
Reed, R. K., An estimate of the climatological heat fluxes over the tropical Pacific
Ocean, J. Clim. Appl. Meteorol., 24, 833-840, 1985.
Reynolds, R. W., A real-time global sea surface temperature analysis, J. Clim., 1,
75-86, 1988.
Taft, B. A., and M.J. McPhaden, Diurnal cycle of sea surface temperature in the western
tropical Pacific, paper presented at Symposium on Western Tropical Pacific Air-Sea
Interactions, U.S. TOGA Project Office, Beijing, China, Nov. 15-17, 1988.
Woods, J. D., and W. Barkmann, The response of the upper ocean to solar heating, I, The
mixed layer. Q. J. R. Meteorol. Soc., 112, 1-28, 1986.
Figure Captions
Fig. 1
. (a) Average SST and (b) SST anomaly in the western tropical
Pacific for December 1986 to October 1987, based on data from the National Meteorological
Center [Reynolds, 1988]. Contour interval is 1°C in Figure 1a, except that
the 29.5°C isotherm is shown as dashed curve. Contour interval in Figure 1b is
0.5°C, with positive values shown as solid contours and negative values shown as dashed
contours. Hatching in Figure 1b indicates regions of negative SST anomaly. The
current meter mooring (solid square) and ATLAS moorings (solid diamonds) are also
indicated.
Fig. 2. (a) Zonal and (b) meridional winds
for December 13, 1986, to October 14, 1987, at 2°N, 0° and 2°S along 165°E.
Fig. 3. Contours of daily averaged temperatures at 2°S,
0°, and 2°N along 165°E for December 13, 1986, to October 14, 1987. Contour interval is
2°C, except that the 29°C contour is shown as a dashed curve. Sensor depths are
indicated on the left axis; 7 days of missing data are indicated by crosses.
Fig. 4. (a) Mean and (b) standard
deviation of temperature between 2°N and 2°S, 165°E for December 13, 1986 to April 16,
1987. Contour interval in Figure 4a is 2°C (except for the 29°C isotherm shown as
a dashed line); contour interval in Figure 4b is 0.2°C, with contours less than
1°C dashed.
Fig. 5. (a) Temperature empirical orthogonal
eigenfunctions (EOF) mode 1 and (b) mode 2 for the period December 13, 1986, to
April 16, 1987. Percent variance explained by each EOF is indicated. Hatching indicates
negative eigenvector values.
Fig. 6. Mode 1 wind EOFs for the period December 13,
1986, to April 16, 1987, in (a) the zonal direction and (b) the meridional
direction. Percent variance explained by each EOF is indicated.
Fig. 7. Time series of daily averaged wind speed (|U|),
zonal wind pseudostress (|U|U ), wind
pseudowork (|U|
), wind
pseudowork (|U| ), SST, and temperature at 50 m (dashed
curve) from the current meter mooring at 0°, 165°E for the period December 13, 1986, to
October 14, 1987. Note that 50-m temperatures are off-scale frequently after August 1987
because the upper thermocline has risen to this depth by then (see Figure 3).
), SST, and temperature at 50 m (dashed
curve) from the current meter mooring at 0°, 165°E for the period December 13, 1986, to
October 14, 1987. Note that 50-m temperatures are off-scale frequently after August 1987
because the upper thermocline has risen to this depth by then (see Figure 3).
Fig. 8. Cross correlations between SST and wind speed,
zonal wind pseudostress, and wind pseudowork. Cross correlation extrema (r) and the
lag (in days) at which they occur are shown. In each case, the lag indicates that cold SST
follows high winds by 1 day. The 95% confidence limits for the null hypothesis of
uncorrelated variability are indicated by horizontal bars on the abscissa.
Fig. 9. Coherence and phase spectra for SST and wind
speed, zonal wind pseudostress, and wind pseudowork at 0°, 165°E for the period December
13, 1986, to October 14, 1987. Positive phase indicates that high winds lead high SST, and
negative phase indicates that high winds lead low SST. Horizontal lines superimposed on
coherence estimates indicate 95% confidence limits for the null hypothesis of incoherent
variability, based on five (15) frequency band averages at periods longer (shorter) than
about 8 days.
Fig. 10. Coherence amplitude as a function of depth
averaged over periods of approximately 3-8 days (encompassing 36-65 frequency bands
depending on depth) for SST and wind speed, zonal wind pseudostress, and wind pseudowork
at 0°, 165°E. The 95% confidence limits for the null hypothesis of incoherent
variability are indicated by the dashed lines. Note that the temperature record lengths
for this analysis were chosen such that the statistics were stationary; for example, the
period June-October 1987 was excluded at 50 m and 75 m. Shown on the right are the mean
temperature profile (solid curve) and the standard deviation of temperature variations at
periods of approximately 3-8 days (dashed curve) for December 13, 1986, to October 14,
1987.
Fig. 11. Coherence amplitude as a function of depth
averaged over periods of approximately 30-60 days (that is 4-6 frequency bands, depending
on depth) for SST and wind speed, zonal wind pseudostress, and wind pseudowork at 0°,
165°E. The 95% confidence limits for the null hypothesis of incoherent variability are
indicated by the dashed lines. Shown on the right are the mean temperature profile (solid
curve) and the standard deviation of temperature variations at periods of approximately
30-60 days (dashed curve) for December 13, 1986, to October 14, 1987.
Fig. 12. Coherence amplitude and phase as a function of
depth averaged over periods of approximately 3-8 days (encompassing 36-65 frequency bands,
depending on depth) for SST and zonal wind pseudostress at 0°, 165°E. The 95% confidence
limits for the null hypothesis of incoherent variability are indicated by the dashed
curve.
Fig. 13. Time series of  H/
H/ t for depth ranges of (a)
0-10 m for the period December 13, 1986, to July 20, 1987, and (b) 0-75 m for the
period December 13, 1986, to May 31, 1987. The standard deviation of heat content
variations (
t for depth ranges of (a)
0-10 m for the period December 13, 1986, to July 20, 1987, and (b) 0-75 m for the
period December 13, 1986, to May 31, 1987. The standard deviation of heat content
variations (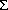 ) and cross correlation with wind speed at
zero lag (r) are shown.
) and cross correlation with wind speed at
zero lag (r) are shown.
Fig. 14. Zonal velocity (u), meridional velocity
(v), and time rate of change of temperature ( T/
T/ T) at 50 m from December 13, 1986, to May 31, 1987, at 0°,
165°E. Daily averaged data are shown by thin curves and 15-day Hanning filtered data are
shown by thick curves.
T) at 50 m from December 13, 1986, to May 31, 1987, at 0°,
165°E. Daily averaged data are shown by thin curves and 15-day Hanning filtered data are
shown by thick curves.
Table 1. Summary of means and
standard deviations for wind speed, zonal wind pseudostress, pseudowork, and sea surface
temperature from the current meter mooring at 0°, 165°E for the period from December 13,
1986, to October 14, 1987.
Return to Abstract
PMEL Outstanding Papers
PMEL Publications Search
PMEL Homepage
ryan.layne.whitney@noaa.gov
 29°C) and frequent outbreaks of westerly winds. We infer
that evaporative cooling related to wind speed variations accounts for a significant
fraction of the observed sea surface temperature (SST) and upper ocean heat content
variability. This evaporative heat flux converges nonlinearly in the surface layer, giving
rise to larger temperature variations in the upper 10 m than below. Other processes
examined (wind-forced vertical advection and entrainment, lateral advection) were
negligible or of secondary importance relative to evaporative cooling. A large fraction of
the SST and surface layer heat content variance could not be directly related to wind
fluctuations; this unexplained variance is probably related to shortwave radiative fluxes
at the air-sea interface.
29°C) and frequent outbreaks of westerly winds. We infer
that evaporative cooling related to wind speed variations accounts for a significant
fraction of the observed sea surface temperature (SST) and upper ocean heat content
variability. This evaporative heat flux converges nonlinearly in the surface layer, giving
rise to larger temperature variations in the upper 10 m than below. Other processes
examined (wind-forced vertical advection and entrainment, lateral advection) were
negligible or of secondary importance relative to evaporative cooling. A large fraction of
the SST and surface layer heat content variance could not be directly related to wind
fluctuations; this unexplained variance is probably related to shortwave radiative fluxes
at the air-sea interface.  1°C
1°C



 (1)
(1)
 T/
T/ , is an entrainment velocity through the base
of the mixed layer at depth z = -h, and Q
, is an entrainment velocity through the base
of the mixed layer at depth z = -h, and Q is surface heat flux. The horizontal temperature gradient
is denoted by
is surface heat flux. The horizontal temperature gradient
is denoted by 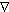 T, and
T, and  T
T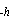 is the change in temperature at the base of the mixed layer. Water density (
is the change in temperature at the base of the mixed layer. Water density (
 )
are assumed constant at 10
)
are assumed constant at 10 kg m
kg m and 3.94 × 10
and 3.94 × 10 °C
°C (= 1.2 kg m
(= 1.2 kg m are generally the larger of
the two turbulent fluxes in the western equatorial Pacific
are generally the larger of
the two turbulent fluxes in the western equatorial Pacific 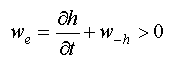 (3)
(3)
 is a drag coefficient and U
is a drag coefficient and U is zonal wind speed.
is zonal wind speed. 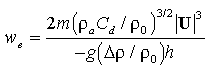 (5)
(5)
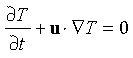 (6)
(6)




 s
s





 ) and cross correlation with wind speed at zero lag (r)
are shown.
) and cross correlation with wind speed at zero lag (r)
are shown. 
 35 W m
35 W m )
for wind-speed-related temperature variations of 3-4 days (based on the cross-correlation
analysis in
)
for wind-speed-related temperature variations of 3-4 days (based on the cross-correlation
analysis in 