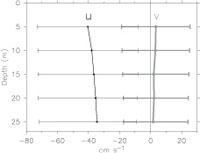
Fig. 1. The mean zonal (black) and meridional (gray) currents (cm s−1) at 2°N, 140°W with ±1 standard deviation indicated at 5, 10, 15, 20, and 25 m, computed for the period 24 May–7 Oct 2004.
The mean flow above 25 m was primarily westward, with a very weak poleward component, for the period 24 May–7 October 2004 (Fig. 1). The mean westward component was 41 cm s−1 at 5 m, decreasing to 35 cm s−1 at 25 m, while the mean poleward component was only 3.3 cm s−1 at 5 m, decreasing to 1.6 cm s−1 at 25 m. For the full period 24 May 2004–28 February 2005, the mean westward currents above 20 m were stronger by ∼15 cm s−1, but the poleward currents were still under 4 cm s−1 (not shown).
Observed poleward currents and shear were substantially weaker than the 6 cm s−1 currents at 20 m and (2 cm s−1)/10-m poleward shear at 25 m found at 2°N by Johnson et al. (2001) from nine years of shipboard ADCP data between 95° and 170°W. Based upon this shear, Johnson et al. extrapolated the shipboard ADCP measurements to the surface to estimate a 10 cm s−1 poleward surface current at 2°N (about 3 times larger than we observed). Our observed weak poleward currents at 2°N, 140°W are even more curious when one considers the implications for the meridional overturning cell transport. Estimates of equatorial upwelling made over the two decades since Wyrtki (1981) have ranged from 30 Sv (Meinen et al. 2001) to 60 Sv (Sv ≡ 106 m3 s−1) (Johnson et al. 2001), the great majority of which must occur equatorward of 2° latitude. Likewise, because 140°W is a central longitude within the cold tongue system, where easterly trades are near their maximum, one might expect 140°W to have larger poleward currents than the zonal average and thus the implied transport to be an upper bound estimate. However, the measured poleward currents at 2°N, 140°W, if representative of the currents across the 80° longitude of the cold tongue, imply a poleward transport of only 7 Sv. With a similar transport assumed for the Southern Hemisphere, the implied equatorial upwelling transport is only 14 Sv, less than half of the lowest estimate. Winds during the study period were not anomalous compared to climatology (not shown). It is possible that at the cold tongue front a local minimum in the near-surface poleward currents exists that is not resolved in the Johnson et al. (2001) mean section owing to the considerable temporal, meridional, and zonal averaging done in that analysis. If this local minimum feature is real, then what causes it? What happens to the poleward branch of the tropical cell at the front? What physics control the structures of zonal and meridional shear?
Fig. 2. Vectors of the 2°N, 140°W mean wind (blue) and currents relative to 25 m (black) with their geostrophic (green) and ageostrophic (brown) components, as (a) observed for the period 24 May–7 Oct 2004 and as simulated by the (b) classical, (c) frontal, and (d) generalized Ekman models. The wind shown in (a) is the vector wind speed and in (b)−(d) is the wind stress vector. The surface geostrophic stress (τp = ρ0v ∂ug/∂z) and effective wind stress (τeff = τ0 − τp) are also shown in (c). The magnitudes of the wind and relative currents are indicated by the circles. Units for the relative currents are cm s−1, m s−1 for wind speed, and 10−2 N m−2 for wind stress. Currents at 5, 10, 15, and 20 m, relative to 25 m, can be distinguished by their decreasing amplitude. Standard errors are indicated by the ellipses on the arrow heads. The vectors in (a) are superimposed upon the mean TMI SST field.
Because the observed poleward shear is so weak, the mean currents relative to 25 m are nearly westward and thus, surprisingly, are to the left of the mean winds (Fig. 2a). The 2°N, 140°W site, however, is in the cold tongue front, with warm water to the north and west, and therefore the observed shear has a geostrophic component that is southwestward, parallel to the SST contours. When the geostrophic shear is subtracted from the observed currents, the residual ageostrophic currents relative to 25 m are predominantly northward and have the appearance of an Ekman spiral (Fig. 2a). In particular, the 5-m ageostrophic current referenced to 25 m is oriented 71° to the right of the wind, and at each subsequent depth the ageostrophic current referenced to 25 m is weaker and tends to be oriented to the right of the ageostrophic currents above.
If the observed ageostrophic spiral is interpreted as a classical Ekman spiral forced by the wind stress (4), then the orientation of the 5-m ageostrophic current relative to 25 m would suggest that the reference depth of 25 m is near the e-folding ''Ekman depth,'', ![]() , (for a classical Ekman spiral, the ageostrophic current has a 1/e decay in magnitude and rotates by 1 rad at this depth). For 2°N, this would imply that the viscosity (v) was ∼ 1.6 × 10−3 m2 s−1. By (4b), though, this would imply that the mean wind stress of 0.07 N m−2 should cause a shear of ∼(0.45 m s−1)(20 m)−1, more than an order of magnitude larger than observed. On the other hand, all Ekman models discussed in sections 1 and 2, (4)–(7), assume that the wind stress balances the surface shear stress according to (2b). Thus for our analysis, we determine v from (2b) with the surface shear estimated from the mean 5- and 15-m currents. The resulting viscosity is an order of magnitude larger—roughly 16 × 10−3 m2 s−1. While this viscosity is quite a bit larger than that given by the Santiago-Mandujano and Firing (1990) relation (5 × 10−3 m2 s−1), other studies (F. Bonjean 2008, personal communication) have also found that the Santiago-Mandujano and Firing (1990) viscosity appear to be biased low. With v set as 16 × 10−3 m2 s−1, the Ekman depth is ∼80 m and the ageostrophic shears above 25 m resulting from the classical Ekman model more closely parallel the wind stress (Fig. 2b). As a consequence, the observed near-surface shears cannot be reproduced as a linear combination of thermal wind shear plus classical Ekman spiral shear.
, (for a classical Ekman spiral, the ageostrophic current has a 1/e decay in magnitude and rotates by 1 rad at this depth). For 2°N, this would imply that the viscosity (v) was ∼ 1.6 × 10−3 m2 s−1. By (4b), though, this would imply that the mean wind stress of 0.07 N m−2 should cause a shear of ∼(0.45 m s−1)(20 m)−1, more than an order of magnitude larger than observed. On the other hand, all Ekman models discussed in sections 1 and 2, (4)–(7), assume that the wind stress balances the surface shear stress according to (2b). Thus for our analysis, we determine v from (2b) with the surface shear estimated from the mean 5- and 15-m currents. The resulting viscosity is an order of magnitude larger—roughly 16 × 10−3 m2 s−1. While this viscosity is quite a bit larger than that given by the Santiago-Mandujano and Firing (1990) relation (5 × 10−3 m2 s−1), other studies (F. Bonjean 2008, personal communication) have also found that the Santiago-Mandujano and Firing (1990) viscosity appear to be biased low. With v set as 16 × 10−3 m2 s−1, the Ekman depth is ∼80 m and the ageostrophic shears above 25 m resulting from the classical Ekman model more closely parallel the wind stress (Fig. 2b). As a consequence, the observed near-surface shears cannot be reproduced as a linear combination of thermal wind shear plus classical Ekman spiral shear.
Alternatively, according to the frontal Ekman model (5), the ageostrophic Ekman spiral responds only to that portion of the wind stress that is not balanced by the geostrophic shear (τeff = τ0 − ρ0ν∂ug/∂z). As shown in Fig. 2c, with viscosity set as 16 × 10−3 m2 s−1, the stress associated with the surface geostrophic shear (τp = ρ0ν∂ug/∂z) is slightly larger in magnitude than the wind stress and is oriented to the southwest while the wind stress is oriented to the northwest. Thus, the net effective stress (τeff) forcing the surface ageostrophic shear is roughly northward. The resulting frontal Ekman model ageostrophic currents relative to 25 m are in good agreement with the observed residual ageostrophic currents. Furthermore, when thermal wind is added to the modeled ageostrophic currents, the resulting total currents relative to 25 m are to the left of the wind stress as observed.
As discussed in the introduction, a perhaps more realistic model of the near-surface shear is the generalized Ekman model (7) in which viscosity decays with depth to zero at z = −H. The difficulty of testing this model is that we do not know what the n profile is, nor at what depth it goes to zero, nor what the profile of the buoyancy gradient is. Furthermore, the deepest current observations are at 25 m and the primary differences between the frontal and generalized Ekman models are likely to be below this depth. For simplicity and because the Peters et al. (1988) turbulence measurements indicate that viscosity decays exponentially with depth, we assume viscosity has the form:
v = A exp(z/D) − B.
It is beyond the scope of this paper and dataset to do a full sensitivity analysis of the parameter space. We therefore arbitrarily set D to be the top of the thermocline (125 m) and choose A and B so that the viscosity is equivalent to 16 × 10−3 m2 s−1 at 10-m depth and zero at the arbitrary depth of 250 m (twice the decay scale). Likewise, for simplicity, we assume that the front is uniform within the frictional layer above 250 m. The resulting generalized Ekman model (Fig. 2d) produces currents relative to 25 m that are to the left of the wind, similar to the results of the frontal Ekman model (Fig. 2c) and to the observations (Fig. 2a).
Although total currents relative to 25 m predicted by both the frontal and generalized Ekman models show some indication of rotation to the left with depth, the observed currents relative to 25 m do not. The standard error (shown as ellipses around the vector heads in Fig. 2a) suggests that this wobble is real. This error, however, does not include any systematic biases and therefore underestimates the true error. If the wobble in orientation is real, it is likely caused by more complicated vertical structures in the viscosity and horizontal density gradients than assumed here.
Return to Previous section
Go to Next section